Aufgaben:Aufgabe 3.4Z: Äquivalente Faltungscodes?: Unterschied zwischen den Versionen
| (15 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Algebraische und polynomische Beschreibung}} | {{quiz-Header|Buchseite=Kanalcodierung/Algebraische und polynomische Beschreibung}} | ||
| − | [[Datei:P_ID2666__KC_Z_3_4.png|right|Nichtsystematischer und systematischer Faltungscodierer]] | + | [[Datei:P_ID2666__KC_Z_3_4.png|right|frame|Nichtsystematischer und <br>systematischer Faltungscodierer]] |
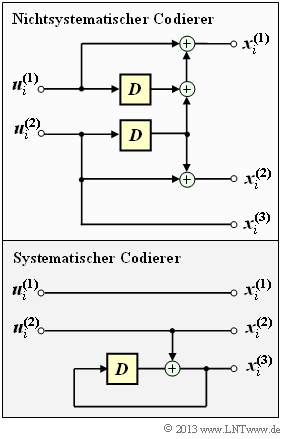
| − | Die obere Darstellung zeigt einen Faltungscodierer, der | + | Die obere Darstellung zeigt einen Faltungscodierer, der durch folgende Gleichungen beschrieben wird: |
:$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},$$ | :$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},$$ | ||
:$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i-1}^{(2)} \hspace{0.05cm},$$ | :$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i-1}^{(2)} \hspace{0.05cm},$$ | ||
| Zeile 8: | Zeile 8: | ||
Gesucht sind die Übertragungsfunktionsmatrizen | Gesucht sind die Übertragungsfunktionsmatrizen | ||
| − | * $\mathbf{G}(D)$ dieses nichtsystematischen Codes, und | + | * $\mathbf{G}(D)$ dieses nichtsystematischen Codes, und |
| − | * $\mathbf{G}_{\rm sys}(D)$ des äquivalenten systematischen Codes. | + | * $\mathbf{G}_{\rm sys}(D)$ des äquivalenten systematischen Codes. |
| − | Die Matrix $\mathbf{G}_{\rm sys}(D)$ erhält man in folgender Weise: | + | Die Matrix $\mathbf{G}_{\rm sys}(D)$ erhält man in folgender Weise: |
| − | * Man spaltet von der $k × n$–Matrix $\mathbf{G}(D)$ vorne eine quadratische Matrix $\mathbf{T}(D)$ mit jeweils $k$ | + | * Man spaltet von der $k × n$–Matrix $\mathbf{G}(D)$ vorne eine quadratische Matrix $\mathbf{T}(D)$ mit jeweils $k$ Zeilen und Spalten ab. Den Rest bezeichnet man mit $\mathbf{Q}(D)$. |
| − | * Anschließend berechnet man die zu $\mathbf{T}(D)$ inverse Matrix $\mathbf{T}^{ | + | * Anschließend berechnet man die zu $\mathbf{T}(D)$ inverse Matrix $\mathbf{T}^{-1}(D)$ und daraus die gesuchte Matrix für den äquivalenten systematischen Code: |
:$${\boldsymbol{\rm G}}_{\rm sys}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm G}}(D) \hspace{0.05cm}.$$ | :$${\boldsymbol{\rm G}}_{\rm sys}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm G}}(D) \hspace{0.05cm}.$$ | ||
| − | * Da $\mathbf{T}^{–1}(D) \cdot \mathbf{T}(D)$ die $k × k$–Einheitsmatrix $\mathbf{I}_k$ ergibt, kann die Übertragungsfunktionsmatrix des äquivalenten systematischen Codes in der gewünschten Form geschrieben werden: | + | * Da $\mathbf{T}^{–1}(D) \cdot \mathbf{T}(D)$ die $k × k$–Einheitsmatrix $\mathbf{I}_k$ ergibt, kann die Übertragungsfunktionsmatrix des äquivalenten systematischen Codes in der gewünschten Form geschrieben werden: |
:$${\boldsymbol{\rm G}}_{\rm sys}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\big ] | :$${\boldsymbol{\rm G}}_{\rm sys}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\big ] | ||
\hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\boldsymbol{\rm P}}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D) \hspace{0.05cm}. | \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\boldsymbol{\rm P}}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D) \hspace{0.05cm}. | ||
\hspace{0.05cm}$$ | \hspace{0.05cm}$$ | ||
| − | Die untere Schaltung erzeugt mit Sicherheit einen systematischen Code mit gleichen Parametern $k$ und $n$ | + | Die untere Schaltung erzeugt mit Sicherheit einen systematischen Code mit gleichen Parametern $k$ und $n$. |
| − | '' | + | In der Teilaufgabe '''(5)''' ist zu klären, ob es sich dabei tatsächlich um den <i>äquivalenten systematischen Code</i> handelt. Das heißt, ob sich tatsächlich für die beiden Schaltungen genau die gleiche Menge $\{ \hspace{0.1cm} \underline{x} \hspace{0.1cm}\}$ an Codesequenzen ergibt, wenn man alle möglichen Informationssequenzen $\{ \hspace{0.1cm} \underline{u} \hspace{0.1cm} \}$ berücksichtigt. |
| − | * Die Aufgabe | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung| Algebraische und polynomische Beschreibung]]. | ||
| + | * Bezug genommen wird insbesondere auf die Seiten | ||
| + | ::[[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#.C3.9Cbertragungsfunktionsmatrix_.E2.80.93_Transfer_Function_Matrix|Übertragungsfunktionsmatrix – Transfer Function Matrix]] sowie | ||
| + | ::[[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#.C3.84quivalenter_systematischer_Faltungscode|Äquivalenter systematischer Faltungscode]]. | ||
| + | |||
| Zeile 30: | Zeile 42: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie lauten die Parameter des oben dargestellten Codierers? |
| + | |type="{}"} | ||
| + | $k \hspace{0.25cm} = \ ${ 2 } | ||
| + | $n \hspace{0.22cm} = \ ${ 3 } | ||
| + | $m \hspace{0.10cm} = \ ${ 1 } | ||
| + | $ν \hspace{0.28cm} = \ ${ 2 } | ||
| + | $R \hspace{0.18cm} = \ ${ 0.667 3% } | ||
| + | |||
| + | {Welche Form hat die Übertragungsfunktionsmatrix $\mathbf{G}(D)$? | ||
| + | |type="[]"} | ||
| + | + Die erste Zeile von $\mathbf{G}(D)$ lautet $(1 + D, \, 0, \, 0)$. | ||
| + | - Die erste Zeile von $\mathbf{G}(D)$ lautet $(1 + D^2, \, 0, \, D^2)$. | ||
| + | + Die zweite Zeile von $\mathbf{G}(D)$ lautet $(D, \, 1 + D, \, 1)$. | ||
| + | - Die dritte Zeile von $\mathbf{G}(D)$ lautet $(D, \, 1 + D, \, 1)$. | ||
| + | |||
| + | {Geben Sie $\mathbf{T}(D)$ und $\mathbf{T}^{-1}(D)$ an. Wie lautet die Determinante? | ||
| + | |type="()"} | ||
| + | - $\det {\mathbf{T}(D)} = 1$, | ||
| + | - $\det {\mathbf{T}(D)} = D$, | ||
| + | + $\det {\mathbf{T}(D)} = 1 + D^2$. | ||
| + | |||
| + | {Was gilt für die äquivalente systematische Übertragungsfunktionsmatrix? | ||
|type="[]"} | |type="[]"} | ||
| − | + | + | + Die erste Zeile von $\mathbf{G}_{\rm sys}(D)$ lautet $(1, \, 0, \, 0)$. |
| − | - | + | - Die zweite Zeile von $\mathbf{G}_{\rm sys}(D)$ lautet $(0, \, 1, \, 1 + D)$. |
| + | + Die zweite Zeile von $\mathbf{G}_{\rm sys}(D)$ lautet $(0, \, 1, \, 1/(1 + D))$. | ||
| − | { | + | {Sind die beiden vorgegebenen Schaltungen tatsächlich äquivalent? |
| − | |type=" | + | |type="()"} |
| − | + | + JA. | |
| + | - NEIN. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Hier gilt $\underline{k = 2}$ und $\underline{n = 3}$ ⇒ Rate $\underline{R = 2/3}$. |
| − | '''(2)''' | + | *Die Gedächtnisordnung $\underline{m = 1}$ (Anzahl der Speicherelemente pro Eingang). |
| − | '''(3)''' | + | *Die Einflusslänge ist gleich der Summe aller Speicherelemente ⇒ $\underline{\nu = 2}$. |
| − | '''(4)''' | + | |
| − | '''(5)''' | + | |
| + | |||
| + | '''(2)''' Das Informationsbit $u_i^{(1)}$ beeinflusst nur den ersten Ausgang $x_i^{(1)}$, während $u_i^{(2)}$ für $x_i^{(2)}$ und $x_i^{(3)}$ herangezogen wird. | ||
| + | *Damit erhält man für die nullte [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#Aufteilung_der_Generatormatrix_in_Teilmatrizen| Teilmatrix]]: | ||
| + | :$${ \boldsymbol{\rm G}}_0 = | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & 0\\ | ||
| + | 0 & 1 & 1 | ||
| + | \end{pmatrix} \hspace{0.05cm}. $$ | ||
| + | |||
| + | *Die verzögerten Eingänge wirken sich wie folgt aus: | ||
| + | ** $u_{i–1}^{(1)}$ beeinflusst $x_i^{(1)}$, | ||
| + | ** $u_{i–1}^{(2)}$ beeinflusst $x_i^{(1)}$ und $x_i^{(2)}$: | ||
| + | |||
| + | |||
| + | *Somit lauten die Teilmatrix $\mathbf{G}_1$ und die Übertragungsfunktionsmatrix $\mathbf{G}(D)$: | ||
| + | :$${ \boldsymbol{\rm G}}_1 = | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & 0\\ | ||
| + | 1 & 1 & 0 | ||
| + | \end{pmatrix} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}(D) = { \boldsymbol{\rm G}}_0 + { \boldsymbol{\rm G}}_1 \cdot D = | ||
| + | \begin{pmatrix} | ||
| + | 1+D & 0 & 0\\ | ||
| + | D & 1+D & 1 | ||
| + | \end{pmatrix} | ||
| + | \hspace{0.05cm}. $$ | ||
| + | |||
| + | *Richtig sind demnach die <u>Lösungsvorschläge 1 und 3</u>. | ||
| + | *Die Antwort 2 kann schon allein deshalb nicht stimmen, da bei $m = 1$ in der Übertragungsfunktionsmatrix kein Element mit $D^2$ auftreten kann. | ||
| + | *$\mathbf{G}(D)$ ist zudem eine $2 × 3$–Matrix; eine dritte Zeile gibt es nicht. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Die Aufspaltung von $\mathbf{G}(D)$ ergibt die $2 × 2$–Matrix | ||
| + | :$${ \boldsymbol{\rm T}}(D) = | ||
| + | \begin{pmatrix} | ||
| + | 1+D & 0 \\ | ||
| + | D & 1+D | ||
| + | \end{pmatrix} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm det}\hspace{0.1cm}{ \boldsymbol{\rm T}}(D) = (1+D) \cdot (1+D) = 1+D^2 $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm T}}^{-1}(D) = \frac{1}{1+D^2} \cdot | ||
| + | \begin{pmatrix} | ||
| + | 1+D & 0 \\ | ||
| + | D & 1+D | ||
| + | \end{pmatrix} \hspace{0.05cm}. $$ | ||
| + | |||
| + | *Richtig ist der <u>Lösungsvorschlag 3</u>. Zur Kontrolle: | ||
| + | :$${ \boldsymbol{\rm T}}(D) \cdot { \boldsymbol{\rm T}}^{-1}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | ||
| + | \frac{1}{1+D^2} \cdot | ||
| + | \begin{pmatrix} | ||
| + | 1+D & 0 \\ | ||
| + | D & 1+D | ||
| + | \end{pmatrix} \cdot | ||
| + | \begin{pmatrix} | ||
| + | 1+D & 0 \\ | ||
| + | D & 1+D | ||
| + | \end{pmatrix} =$$ | ||
| + | :$$ \ = \ \hspace{-0.15cm} ... \hspace{0.1cm}= \frac{1}{1+D^2} \cdot | ||
| + | \begin{pmatrix} | ||
| + | 1+D^2 & 0 \\ | ||
| + | 0 & 1+D^2 | ||
| + | \end{pmatrix} = \begin{pmatrix} | ||
| + | 1 & 0 \\ | ||
| + | 0 & 1 | ||
| + | \end{pmatrix}\hspace{0.05cm}. $$ | ||
| + | |||
| + | |||
| + | '''(4)''' Entsprechend dem Angabenblatt gilt: | ||
| + | :$${ \boldsymbol{\rm P}}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} { \boldsymbol{\rm T}}^{-1}(D) \cdot { \boldsymbol{\rm Q}}(D) = \frac{1}{1+D^2} \cdot | ||
| + | \begin{pmatrix} | ||
| + | 1+D & 0 \\ | ||
| + | D & 1+D | ||
| + | \end{pmatrix} | ||
| + | \cdot | ||
| + | \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 1 | ||
| + | \end{pmatrix} =$$ | ||
| + | :$$\ = \ \hspace{-0.15cm} \frac{1}{1+D^2} \cdot | ||
| + | \begin{pmatrix} | ||
| + | (1+D)\cdot 0 + 0 \cdot 1 \\ | ||
| + | D\cdot 0 + (1+D)\cdot 1 | ||
| + | \end{pmatrix} = \frac{1}{1+D^2} \cdot | ||
| + | \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 1+D | ||
| + | \end{pmatrix} = \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 1/(1+D) | ||
| + | \end{pmatrix} $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} {\boldsymbol{\rm G}}_{\rm sys}(D) | ||
| + | = \begin{pmatrix} | ||
| + | 1 & 0 & 0\\ | ||
| + | 0 & 1 & 1/(1+D) | ||
| + | \end{pmatrix}\hspace{0.05cm}. $$ | ||
| + | |||
| + | *Richtig ist demnach die <u>Lösungsvorschläge 1 und 3</u>. | ||
| + | |||
| + | |||
| + | '''(5)''' Richtig ist <u>JA</u>. Die untere Schaltung auf dem Angabenblatt ist gekennzeichnet durch die Gleichungen $x_i^{(1)} = u_i^{(1)}$ und $x_i^{(2)} = u_i^{(2)}$ sowie | ||
| + | :$$x_i^{(3)}= x_{i-1}^{(3)} + u_i^{(2)} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} | ||
| + | X^{(3)}(D)= X^{(3)}(D) \cdot D +U^{(2)}(D)$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} G(D) = \frac {X^{(3)}(D)}{U^{(2)}(D)} = \frac {1}{1+D} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Dies entspricht genau dem letzten Element von $\mathbf{G}_{\rm sys}(D)$ entsprechend der Teilaufgabe (4). | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Kanalcodierung|^3.2 | + | [[Category:Aufgaben zu Kanalcodierung|^3.2 Polynomische Beschreibung |
Aktuelle Version vom 6. Juni 2019, 17:09 Uhr
Die obere Darstellung zeigt einen Faltungscodierer, der durch folgende Gleichungen beschrieben wird:
- $$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},$$
- $$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i-1}^{(2)} \hspace{0.05cm},$$
- $$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)}\hspace{0.05cm}.$$
Gesucht sind die Übertragungsfunktionsmatrizen
- $\mathbf{G}(D)$ dieses nichtsystematischen Codes, und
- $\mathbf{G}_{\rm sys}(D)$ des äquivalenten systematischen Codes.
Die Matrix $\mathbf{G}_{\rm sys}(D)$ erhält man in folgender Weise:
- Man spaltet von der $k × n$–Matrix $\mathbf{G}(D)$ vorne eine quadratische Matrix $\mathbf{T}(D)$ mit jeweils $k$ Zeilen und Spalten ab. Den Rest bezeichnet man mit $\mathbf{Q}(D)$.
- Anschließend berechnet man die zu $\mathbf{T}(D)$ inverse Matrix $\mathbf{T}^{-1}(D)$ und daraus die gesuchte Matrix für den äquivalenten systematischen Code:
- $${\boldsymbol{\rm G}}_{\rm sys}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm G}}(D) \hspace{0.05cm}.$$
- Da $\mathbf{T}^{–1}(D) \cdot \mathbf{T}(D)$ die $k × k$–Einheitsmatrix $\mathbf{I}_k$ ergibt, kann die Übertragungsfunktionsmatrix des äquivalenten systematischen Codes in der gewünschten Form geschrieben werden:
- $${\boldsymbol{\rm G}}_{\rm sys}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\big ] \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\boldsymbol{\rm P}}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D) \hspace{0.05cm}. \hspace{0.05cm}$$
Die untere Schaltung erzeugt mit Sicherheit einen systematischen Code mit gleichen Parametern $k$ und $n$.
In der Teilaufgabe (5) ist zu klären, ob es sich dabei tatsächlich um den äquivalenten systematischen Code handelt. Das heißt, ob sich tatsächlich für die beiden Schaltungen genau die gleiche Menge $\{ \hspace{0.1cm} \underline{x} \hspace{0.1cm}\}$ an Codesequenzen ergibt, wenn man alle möglichen Informationssequenzen $\{ \hspace{0.1cm} \underline{u} \hspace{0.1cm} \}$ berücksichtigt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Algebraische und polynomische Beschreibung.
- Bezug genommen wird insbesondere auf die Seiten
Fragebogen
Musterlösung
- Die Gedächtnisordnung $\underline{m = 1}$ (Anzahl der Speicherelemente pro Eingang).
- Die Einflusslänge ist gleich der Summe aller Speicherelemente ⇒ $\underline{\nu = 2}$.
(2) Das Informationsbit $u_i^{(1)}$ beeinflusst nur den ersten Ausgang $x_i^{(1)}$, während $u_i^{(2)}$ für $x_i^{(2)}$ und $x_i^{(3)}$ herangezogen wird.
- Damit erhält man für die nullte Teilmatrix:
- $${ \boldsymbol{\rm G}}_0 = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}. $$
- Die verzögerten Eingänge wirken sich wie folgt aus:
- $u_{i–1}^{(1)}$ beeinflusst $x_i^{(1)}$,
- $u_{i–1}^{(2)}$ beeinflusst $x_i^{(1)}$ und $x_i^{(2)}$:
- Somit lauten die Teilmatrix $\mathbf{G}_1$ und die Übertragungsfunktionsmatrix $\mathbf{G}(D)$:
- $${ \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 & 0 & 0\\ 1 & 1 & 0 \end{pmatrix} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}(D) = { \boldsymbol{\rm G}}_0 + { \boldsymbol{\rm G}}_1 \cdot D = \begin{pmatrix} 1+D & 0 & 0\\ D & 1+D & 1 \end{pmatrix} \hspace{0.05cm}. $$
- Richtig sind demnach die Lösungsvorschläge 1 und 3.
- Die Antwort 2 kann schon allein deshalb nicht stimmen, da bei $m = 1$ in der Übertragungsfunktionsmatrix kein Element mit $D^2$ auftreten kann.
- $\mathbf{G}(D)$ ist zudem eine $2 × 3$–Matrix; eine dritte Zeile gibt es nicht.
(3) Die Aufspaltung von $\mathbf{G}(D)$ ergibt die $2 × 2$–Matrix
- $${ \boldsymbol{\rm T}}(D) = \begin{pmatrix} 1+D & 0 \\ D & 1+D \end{pmatrix} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm det}\hspace{0.1cm}{ \boldsymbol{\rm T}}(D) = (1+D) \cdot (1+D) = 1+D^2 $$
- $$\Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm T}}^{-1}(D) = \frac{1}{1+D^2} \cdot \begin{pmatrix} 1+D & 0 \\ D & 1+D \end{pmatrix} \hspace{0.05cm}. $$
- Richtig ist der Lösungsvorschlag 3. Zur Kontrolle:
- $${ \boldsymbol{\rm T}}(D) \cdot { \boldsymbol{\rm T}}^{-1}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac{1}{1+D^2} \cdot \begin{pmatrix} 1+D & 0 \\ D & 1+D \end{pmatrix} \cdot \begin{pmatrix} 1+D & 0 \\ D & 1+D \end{pmatrix} =$$
- $$ \ = \ \hspace{-0.15cm} ... \hspace{0.1cm}= \frac{1}{1+D^2} \cdot \begin{pmatrix} 1+D^2 & 0 \\ 0 & 1+D^2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\hspace{0.05cm}. $$
(4) Entsprechend dem Angabenblatt gilt:
- $${ \boldsymbol{\rm P}}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} { \boldsymbol{\rm T}}^{-1}(D) \cdot { \boldsymbol{\rm Q}}(D) = \frac{1}{1+D^2} \cdot \begin{pmatrix} 1+D & 0 \\ D & 1+D \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} =$$
- $$\ = \ \hspace{-0.15cm} \frac{1}{1+D^2} \cdot \begin{pmatrix} (1+D)\cdot 0 + 0 \cdot 1 \\ D\cdot 0 + (1+D)\cdot 1 \end{pmatrix} = \frac{1}{1+D^2} \cdot \begin{pmatrix} 0 \\ 1+D \end{pmatrix} = \begin{pmatrix} 0 \\ 1/(1+D) \end{pmatrix} $$
- $$\Rightarrow \hspace{0.3cm} {\boldsymbol{\rm G}}_{\rm sys}(D) = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 1/(1+D) \end{pmatrix}\hspace{0.05cm}. $$
- Richtig ist demnach die Lösungsvorschläge 1 und 3.
(5) Richtig ist JA. Die untere Schaltung auf dem Angabenblatt ist gekennzeichnet durch die Gleichungen $x_i^{(1)} = u_i^{(1)}$ und $x_i^{(2)} = u_i^{(2)}$ sowie
- $$x_i^{(3)}= x_{i-1}^{(3)} + u_i^{(2)} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} X^{(3)}(D)= X^{(3)}(D) \cdot D +U^{(2)}(D)$$
- $$\Rightarrow \hspace{0.3cm} G(D) = \frac {X^{(3)}(D)}{U^{(2)}(D)} = \frac {1}{1+D} \hspace{0.05cm}.$$
Dies entspricht genau dem letzten Element von $\mathbf{G}_{\rm sys}(D)$ entsprechend der Teilaufgabe (4).