Aufgaben:Aufgabe 3.13: Nochmals zu den Pfadgewichtsfunktionen: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
[[Datei:P_ID2711__KC_A_3_13.png|right|frame|Zur Reduktion des Zustandsübergangsdiagramms]] | [[Datei:P_ID2711__KC_A_3_13.png|right|frame|Zur Reduktion des Zustandsübergangsdiagramms]] | ||
| − | Auf der Seite [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Regeln_zur_Manipulation_des_Zustands.C3.BCbergangsdiagramms|Regeln zur Manipulation des Zustandsübergangsdiagramms]] wurde für das Beispiel unseres Rate–1/2–Standardcodes mit Gedächtnis $m = 2$ und der Übertragungsfunktionsmatrix | + | Auf der Seite [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Regeln_zur_Manipulation_des_Zustands.C3.BCbergangsdiagramms|Regeln zur Manipulation des Zustandsübergangsdiagramms]] wurde für das Beispiel unseres Rate–1/2–Standardcodes mit Gedächtnis $m = 2$ und der Übertragungsfunktionsmatrix |
:$${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big )$$ | :$${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big )$$ | ||
die Berechnung der Pfadgewichtsfunktionen sehr ausführlich beschrieben. Als Ergebnisse wurden genannt: | die Berechnung der Pfadgewichtsfunktionen sehr ausführlich beschrieben. Als Ergebnisse wurden genannt: | ||
| − | :$$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \ | + | :$$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$ |
| − | :$$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \ | + | :$$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$ |
| − | Nun sollen die gleichen Berechnungen für den [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#Systematische_Faltungscodes|äquivalenten systematischen Code]] mit der Übertragungsfunktionsmatrix | + | Nun sollen die gleichen Berechnungen für den [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#Systematische_Faltungscodes|äquivalenten systematischen Code]] mit der Übertragungsfunktionsmatrix |
:$${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big )$$ | :$${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big )$$ | ||
durchgeführt werden. | durchgeführt werden. | ||
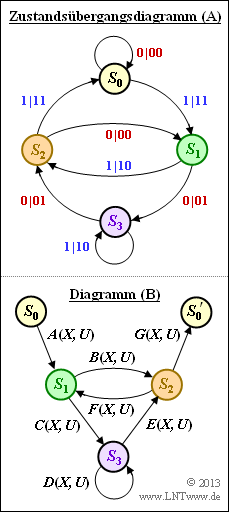
| − | Die Grafik zeigt das Zustandsübergangsdiagramm | + | *Die Grafik zeigt das Zustandsübergangsdiagramm $\rm (A)$ und die Struktur des reduzierten Diagramms $\rm (B)$, wobei die Übergänge mit $A(X, \, U), \ \text{...}\ , \ G(X, \, U)$ allgemein bezeichnet sind. |
| + | *In der Teilaufgabe '''(1)''' sollen diese Abkürzungen an das Zustandsübergangsdiagramm $\rm (A)$ angepasst werden. | ||
| + | |||
| + | |||
| + | |||
| Zeile 22: | Zeile 26: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabegehört zum Kapitel [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken| Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken]]. | + | * Die Aufgabegehört zum Kapitel [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken| Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken]]. |
| − | * Zur Lösung der Teilaufgaben (2) und (3) verweisen wir hier nochmals auf die Seite [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Regeln_zur_Manipulation_des_Zustands.C3.BCbergangsdiagramms|Regeln zur Manipulation des Zustandsübergangsdiagramms]] im Theorieteil. | + | * Zur Lösung der Teilaufgaben '''(2)''' und '''(3)''' verweisen wir hier nochmals auf die Seite [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Regeln_zur_Manipulation_des_Zustands.C3.BCbergangsdiagramms|Regeln zur Manipulation des Zustandsübergangsdiagramms]] im Theorieteil. |
| Zeile 45: | Zeile 49: | ||
+ Keiner der Vorschläge ist richtig. | + Keiner der Vorschläge ist richtig. | ||
| − | { | + | {Welche Ausdrücke gelten für die „einfache” Pfadgewichtsfunktion? |
|type="[]"} | |type="[]"} | ||
+ $T(X) = X^5 \ / \ (1 \, –2X)$. | + $T(X) = X^5 \ / \ (1 \, –2X)$. | ||
| Zeile 54: | Zeile 58: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Der Übergang von $S_0$ nach $S_1$ ist durch „$1 \ | \ 11$” gekennzeichnet. Die Ausgangssequenz $\underline{x}_i = (11)$ wird durch $X^2$ ausgedrückt, das Eingangsbit $u_i = 1$ durch $U$. | + | '''(1)''' <u>Alle Lösungsvorschläge</u> sind richtig. Im angepassten Diagramm $\rm (B)$ sind alle Übergänge eingezeichnet: |
| + | |||
| + | [[Datei:P_ID2712__KC_A_3_13a.png|right|frame|Zur Reduktion des Zustandsübergangsdiagramms]] | ||
| + | |||
| + | *Der Übergang von $S_0$ nach $S_1$ ist durch „$1 \ | \ 11$” gekennzeichnet. | ||
| + | *Die Ausgangssequenz $\underline{x}_i = (11)$ wird durch $X^2$ ausgedrückt, das Eingangsbit $u_i = 1$ durch $U$. | ||
| + | *Das gleiche Ergebnis erhält man für $G(X, \, U)$: | ||
:$$A(X, U) = G(X, U)= UX^2 | :$$A(X, U) = G(X, U)= UX^2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Ausgangssequenzen $\underline{x}_i = (01)$ sowie $\underline{x}_i = (10)$ werden beide mit $X$ markiert. Unter Berücksichtigung der Eingangsbits erhält man somit: | + | *Die Ausgangssequenzen $\underline{x}_i = (01)$ sowie $\underline{x}_i = (10)$ werden beide mit $X$ markiert. |
| − | :$$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm}, | + | *Unter Berücksichtigung der Eingangsbits erhält man somit: |
| − | u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X | + | :$$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$ |
| + | :$$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Der Übergang „$0 \ | \ 00$” von $S_2$ nach $S_1$ wird durch $F(X, \, U) = 1$ ausgedrückt | + | *Der Übergang „$0 \ | \ 00$” von $S_2$ nach $S_1$ wird durch $F(X, \, U) = 1$ ausgedrückt. |
| − | |||
| − | '''(2)''' Entsprechend der Vorgehensweise auf [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Regeln_zur_Manipulation_des_Zustands.C3.BCbergangsdiagramms| | + | '''(2)''' Entsprechend der Vorgehensweise auf der Seite [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Regeln_zur_Manipulation_des_Zustands.C3.BCbergangsdiagramms|Regeln zur Manipulation des Zustandsübergangsdiagramms]] im Theorieteil wird zunächst der Übergang von $S_1$ nach $S_2$ via $S_3$ durch einen <i>Ring</i> zusammengefasst. |
| − | * Man erhält für die rote Hinterlegung im Diagramm (B): | + | * Man erhält für die rote Hinterlegung im Diagramm $\rm (B)$: |
:$$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} | :$$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * Die beiden <i>parallelen Übergänge</i> entsprechend der blauen Hinterlegung im Diagramm (C) können wie folgt | + | * Die beiden <i>parallelen Übergänge</i> entsprechend der blauen Hinterlegung im Diagramm $\rm (C)$ können wie folgt kombiniert werden: |
:$$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = | :$$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = | ||
\frac{X^2 + U- U^2X^2}{1- U X} | \frac{X^2 + U- U^2X^2}{1- U X} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * Die erweiterte Pfadgewichtsfunktion ergibt sich entsprechend Diagramm (D) als <i>Rückkopplung</i>: | + | * Die erweiterte Pfadgewichtsfunktion ergibt sich entsprechend Diagramm $\rm (D)$ als <i>Rückkopplung</i>: |
:$$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} | :$$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} | ||
= \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$ | = \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$ | ||
| − | Dem Autor ist es auch nach mehreren Versuchen nicht gelungen, diesen Ausdruck zielführend weiter zu vereinfachen. Er tendiert zum <u>Lösungsvorschlag 3</u> mit dem Zusatz „ohne Gewähr”. Dieses Ergebnis würde jedoch bedeuten, dass sich die erweiterte Pfadgewichtsfunktion des äquivalenten systematischen Codes von der des nichtsystematischen Codes unterscheidet. Wir werden diese Frage noch mit einem Fachmann klären. | + | Dem Autor ist es auch nach mehreren Versuchen nicht gelungen, diesen Ausdruck zielführend weiter zu vereinfachen. Er tendiert zum <u>Lösungsvorschlag 3</u> mit dem Zusatz „ohne Gewähr”. |
| + | *Dieses Ergebnis würde jedoch bedeuten, dass sich die erweiterte Pfadgewichtsfunktion des äquivalenten systematischen Codes von der des nichtsystematischen Codes unterscheidet. | ||
| + | *Wir werden diese Frage noch mit einem Fachmann klären. | ||
| − | '''(3)''' Setzt man in der erweiterten Funktion $T_{\rm enh}(X, \, U)$ den Formalparameter $U = 1$, so erhält man | + | '''(3)''' Richtig sind die <u>Lösungsvorschläge 1 und 2</u>: |
| + | *Setzt man in der erweiterten Funktion $T_{\rm enh}(X, \, U)$ den Formalparameter $U = 1$, so erhält man den Lösungsvorschlag 1: | ||
:$$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= | :$$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= | ||
\frac{X^5 }{1- X - X} = | \frac{X^5 }{1- X - X} = | ||
\frac{X^5 }{1- 2X} \hspace{0.05cm}.$$ | \frac{X^5 }{1- 2X} \hspace{0.05cm}.$$ | ||
| − | + | *Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + \ \text{...}\ $ kommt man zum Lösungsvorschlag 2. | |
| + | *Das heißt: Die einfache Pfadgewichtsfunktion $T(X)$ stimmt bei beiden Codes überein. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 1. Juli 2019, 16:59 Uhr
Auf der Seite Regeln zur Manipulation des Zustandsübergangsdiagramms wurde für das Beispiel unseres Rate–1/2–Standardcodes mit Gedächtnis $m = 2$ und der Übertragungsfunktionsmatrix
- $${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big )$$
die Berechnung der Pfadgewichtsfunktionen sehr ausführlich beschrieben. Als Ergebnisse wurden genannt:
- $$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$
- $$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$
Nun sollen die gleichen Berechnungen für den äquivalenten systematischen Code mit der Übertragungsfunktionsmatrix
- $${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big )$$
durchgeführt werden.
- Die Grafik zeigt das Zustandsübergangsdiagramm $\rm (A)$ und die Struktur des reduzierten Diagramms $\rm (B)$, wobei die Übergänge mit $A(X, \, U), \ \text{...}\ , \ G(X, \, U)$ allgemein bezeichnet sind.
- In der Teilaufgabe (1) sollen diese Abkürzungen an das Zustandsübergangsdiagramm $\rm (A)$ angepasst werden.
Hinweise:
- Die Aufgabegehört zum Kapitel Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken.
- Zur Lösung der Teilaufgaben (2) und (3) verweisen wir hier nochmals auf die Seite Regeln zur Manipulation des Zustandsübergangsdiagramms im Theorieteil.
Fragebogen
Musterlösung
- Der Übergang von $S_0$ nach $S_1$ ist durch „$1 \ | \ 11$” gekennzeichnet.
- Die Ausgangssequenz $\underline{x}_i = (11)$ wird durch $X^2$ ausgedrückt, das Eingangsbit $u_i = 1$ durch $U$.
- Das gleiche Ergebnis erhält man für $G(X, \, U)$:
- $$A(X, U) = G(X, U)= UX^2 \hspace{0.05cm}.$$
- Die Ausgangssequenzen $\underline{x}_i = (01)$ sowie $\underline{x}_i = (10)$ werden beide mit $X$ markiert.
- Unter Berücksichtigung der Eingangsbits erhält man somit:
- $$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$
- $$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X \hspace{0.05cm}.$$
- Der Übergang „$0 \ | \ 00$” von $S_2$ nach $S_1$ wird durch $F(X, \, U) = 1$ ausgedrückt.
(2) Entsprechend der Vorgehensweise auf der Seite Regeln zur Manipulation des Zustandsübergangsdiagramms im Theorieteil wird zunächst der Übergang von $S_1$ nach $S_2$ via $S_3$ durch einen Ring zusammengefasst.
- Man erhält für die rote Hinterlegung im Diagramm $\rm (B)$:
- $$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} \hspace{0.05cm}.$$
- Die beiden parallelen Übergänge entsprechend der blauen Hinterlegung im Diagramm $\rm (C)$ können wie folgt kombiniert werden:
- $$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = \frac{X^2 + U- U^2X^2}{1- U X} \hspace{0.05cm}.$$
- Die erweiterte Pfadgewichtsfunktion ergibt sich entsprechend Diagramm $\rm (D)$ als Rückkopplung:
- $$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} = \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$
Dem Autor ist es auch nach mehreren Versuchen nicht gelungen, diesen Ausdruck zielführend weiter zu vereinfachen. Er tendiert zum Lösungsvorschlag 3 mit dem Zusatz „ohne Gewähr”.
- Dieses Ergebnis würde jedoch bedeuten, dass sich die erweiterte Pfadgewichtsfunktion des äquivalenten systematischen Codes von der des nichtsystematischen Codes unterscheidet.
- Wir werden diese Frage noch mit einem Fachmann klären.
(3) Richtig sind die Lösungsvorschläge 1 und 2:
- Setzt man in der erweiterten Funktion $T_{\rm enh}(X, \, U)$ den Formalparameter $U = 1$, so erhält man den Lösungsvorschlag 1:
- $$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= \frac{X^5 }{1- X - X} = \frac{X^5 }{1- 2X} \hspace{0.05cm}.$$
- Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + \ \text{...}\ $ kommt man zum Lösungsvorschlag 2.
- Das heißt: Die einfache Pfadgewichtsfunktion $T(X)$ stimmt bei beiden Codes überein.