Applets:WDF und VTF bei Gaußschen 2D Zufallsgrößen (Applet)

Applet in neuem Tab öffnen

Programmbeschreibung

Dieses Applet ermöglicht die Berechnung und graphische Darstellung

• der Wahrscheinlichkeiten ${\rm Pr}(z=\mu)$ einer diskreten Zufallsgröße $z \in \{\mu \} = \{0, 1, 2, 3, \text{...} \}$, welche die Wahrscheinlichkeitsdichtefunktion (WDF) – im Englischen Probability Density Function (PDF) – der Zufallsgröße $z$ bestimmen – hier Darstellung mit Diracfunktionen ${\rm \delta}( z-\mu)$:

$$f_{z}(z)=\sum_{\mu=1}^{M}{\rm Pr}(z=\mu)\cdot {\rm \delta}( z-\mu),$$

• der Wahrscheinlichkeiten ${\rm Pr}(z \le \mu)$ der Verteilungsfunktion (VTF) – im Englischen Cumulative Distribution Function (CDF):

$$F_{z}(\mu)={\rm Pr}(z\le\mu).$$

Als diskrete Verteilungen stehen in zwei Parametersätzen zur Auswahl:

• die Binomialverteilung mit den Parametern $I$ und $p$   ⇒   $z \in \{0, 1, \text{...} \ , I \}$   ⇒   $M = I+1$ mögliche Werte,
• die Poissonverteilung mit Parameter $\lambda$   ⇒   $z \in \{0, 1, 2, 3, \text{...}\}$   ⇒   $M \to \infty$.

In der Versuchsdurchführung sollen Sie miteinander vergleichen:

• je zwei Binomialverteilungen mit unterschiedlichen Parameterwerten $I$ und $p$,
• je zwei Poissonverteilungen mit unterschiedlicher Rate $\lambda$,
• jeweils eine Binomial– und eine Poissonverteilung.

Theoretischer Hintergrund

Verbundwahrscheinlichkeitsdichtefunktion   ⇒   2D–WDF

Wir betrachten zwei wertkontinuierliche Zufallsgrößen  $X$  und  $Y\hspace{-0.1cm}$, zwischen denen statistische Abhängigkeiten bestehen können. Zur Beschreibung der Wechselbeziehungen zwischen diesen Größen ist es zweckmäßig, die beiden Komponenten zu einer  zweidimensionalen Zufallsgröße  $XY =(X, Y)$  zusammenzufassen. Dann gilt:

$\text{Definition:}$  Die  Verbundwahrscheinlichkeitsdichtefunktion  ist die Wahrscheinlichkeitsdichtefunktion (WDF,  englisch:  Probability Density Function, kurz: PDF) der zweidimensionalen Zufallsgröße  $XY$  an der Stelle  $(x, y)$ 

$$f_{XY}(x, \hspace{0.1cm}y) = \lim_{\left.{\Delta x\rightarrow 0 \atop {\Delta y\rightarrow 0} }\right.}\frac{ {\rm Pr}\big [ (x - {\rm \Delta} x/{\rm 2} \le X \le x + {\rm \Delta} x/{\rm 2}) \cap (y - {\rm \Delta} y/{\rm 2} \le Y \le y +{\rm \Delta}y/{\rm 2}) \big] }{ {\rm \Delta} \ x\cdot{\rm \Delta} y}.$$

• Die Verbundwahrscheinlichkeitsdichtefunktion oder kurz  $\text{2D-WDF}$  ist eine Erweiterung der eindimensionalen WDF.
• $∩$  kennzeichnet die logische UND-Verknüpfung.
• $X$  und  $Y$ bezeichnen die beiden Zufallsgrößen, und  $x \in X$  sowie   $y \in Y$ geben Realisierungen hiervon an.
• Die für dieses Applet verwendete Nomenklatur unterscheidet sich also geringfügig gegenüber der Beschreibung im Theorieteil.

Anhand dieser 2D–WDF  $f_{XY}(x, y)$  werden auch statistische Abhängigkeiten innerhalb der zweidimensionalen Zufallsgröße  $XY$  vollständig erfasst im Gegensatz zu den beiden eindimensionalen Dichtefunktionen   ⇒   Randwahrscheinlichkeitsdichtefunktionen:

$$f_{X}(x) = \int _{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}y ,$$

$$f_{Y}(y) = \int_{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}x .$$

Diese beiden Randdichtefunktionen  $f_X(x)$  und  $f_Y(y)$

• liefern lediglich statistische Aussagen über die Einzelkomponenten  $X$  bzw.  $Y$,
• nicht jedoch über die Bindungen zwischen diesen.

2D–WDF bei Gaußschen Zufallsgrößen

Für den Sonderfall  Gaußscher Zufallsgrößen  – der Name geht auf den Wissenschaftler  Carl Friedrich Gauß  zurück – können wir weiterhin vermerken:

• Die Verbund–WDF einer Gaußschen 2D-Zufallsgröße  $XY$  mit Mittelwerten  $m_X = 0$,  $m_Y = 0$  und Korrelationskoeffizienten  $ρ = ρ_{XY}$  lautet:

$$f_{XY}(x,y)=\frac{\rm 1}{\rm 2\it\pi \cdot \sigma_X \cdot \sigma_Y \cdot \sqrt{\rm 1-\rho^2}}\ \cdot\ \exp\Bigg[-\frac{\rm 1}{\rm 2 \cdot (1-\it\rho^{\rm 2} {\rm)}}\cdot(\frac {\it x^{\rm 2}}{\sigma_X^{\rm 2}}+\frac {\it y^{\rm 2}}{\sigma_Y^{\rm 2}}-\rm 2\it\rho\cdot\frac{x \cdot y}{\sigma_x \cdot \sigma_Y}\rm ) \rm \Bigg]\hspace{0.8cm}{\rm mit}\hspace{0.5cm}-1 \le \rho \le +1.$$

• Ersetzt man  $x$  durch  $(x - m_X)$  sowie  $y$  durch  $(y- m_Y)$, so ergibt sich die allgemeinere WDF einer zweidimensionalen Gaußschen Zufallsgröße mit Mittelwert.
• Die Randwahrscheinlichkeitsdichtefunktionen  $f_{X}(x)$  und  $f_{Y}(y)$  einer Gaußschen 2D-Zufallsgröße sind ebenfalls gaußförmig mit den Streuungen  $σ_X$  bzw.  $σ_Y$.
• Bei unkorrelierten Komponenten  $X$  und  $Y$ muss in obiger Gleichung  $ρ = 0$  eingesetzt werden, und man erhält dann das Ergebnis:

$$f_{XY}(x,y)=\frac{1}{\sqrt{2\pi}\cdot\sigma_{X}} \cdot\rm e^{-\it {x^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\hspace{0.05cm}\it\sigma_{X}^{\rm 2}} {\rm )}} \cdot\frac{1}{\sqrt{2\pi}\cdot\sigma_{\it Y}}\cdot e^{-\it {y^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\hspace{0.05cm}\it\sigma_{Y}^{\rm 2}} {\rm )}} = \it f_{X} \rm ( \it x \rm ) \cdot \it f_{Y} \rm ( \it y \rm ) .$$

$\text{Fazit:}$  Im Sonderfall einer 2D-Zufallsgröße mit Gaußscher WDF  $f_{XY}(x, y)$  folgt aus der  Unkorreliertheit  auch direkt die  statistische Unabhängigkeit:

$$f_{XY}(x,y)= f_{X}(x) \cdot f_{Y}(y) . $$

Bitte beachten Sie:

• Bei keiner anderen WDF kann aus der  Unkorreliertheit  auf die  statistische Unabhängigkeit  geschlossen werden.
• Man kann aber stets   ⇒   für jede beliebige 2D–WDF  $f_{XY}(x, y)$  von der  statistischen Unabhängigkeit  auf die  Unkorreliertheit  schließen, weil:
• Sind zwei Zufallsgrößen  $X$  und  $Y$  völlig voneinander (statistisch) unabhängig, so gibt es zwischen ihnen natürlich auch keine linearen  Abhängigkeiten  
  ⇒   sie sind dann auch unkorreliert.

Höhenlinien bei unkorrelierten Zufallsgrößen

Höhenlinien der 2D-WDF bei unkorrelierten Größen

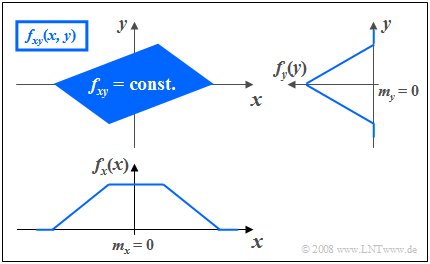
Aus der Bedingungsgleichung  $f_{XY}(x, y) = {\rm const.}$  können die Höhenlinien der WDF berechnet werden.

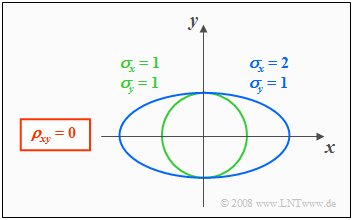
Sind die Komponenten  $X$  und  $Y$ unkorreliert  $(ρ = 0)$, so erhält man als Gleichung für die Höhenlinien:

$$\frac{x^{\rm 2}}{\sigma_{X}^{\rm 2}}+\frac{y^{\rm 2}}{\sigma_{Y}^{\rm 2}} =\rm const.$$

Die Höhenlinien beschreiben in diesem Fall folgende Figuren:

• Kreise  (falls  $σ_X = σ_Y$,   grüne Kurve), oder
• Ellipsen  (für  $σ_X ≠ σ_Y$,   blaue Kurve) in Ausrichtung der beiden Achsen.

Höhenlinien bei korrelierten Zufallsgrößen

Bei korrelierten Komponenten  $(ρ ≠ 0)$  sind die Höhenlinien der WDF stets elliptisch, also auch für den Sonderfall  $σ_X = σ_Y$.

Höhenlinien der 2D-WDF bei korrelierten Größen

Hier lautet die Bestimmungsgleichung der WDF-Höhenlinien:

$$f_{XY}(x, y) = {\rm const.} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \frac{x^{\rm 2} }{\sigma_{X}^{\rm 2}}+\frac{y^{\rm 2} }{\sigma_{Y}^{\rm 2} }-{\rm 2}\cdot\rho\cdot\frac{x\cdot y}{\sigma_X\cdot \sigma_Y}={\rm const.}$$

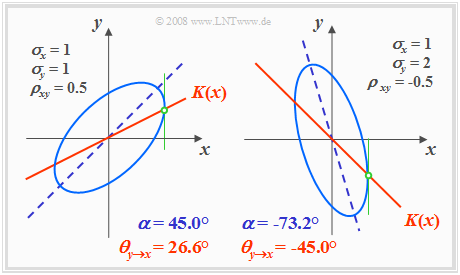
Die Grafik zeigt in hellerem Blau zwei Höhenlinien für unterschiedliche Parametersätze, jeweils mit  $ρ ≠ 0$.

• Die Ellipsenhauptachse ist dunkelblau gestrichelt.
• Die  Korrelationsgerade  $K(x)$  ist durchgehend rot eingezeichnet.

Anhand dieser Darstellung sind folgende Aussagen möglich:

• Die Ellipsenform hängt außer vom Korrelationskoeffizienten $ρ_{xy}$ auch vom Verhältnis der beiden Streuungen $σ_x$ und $σ_y$ ab.
• Der Neigungswinkel $α$ der Ellipsenhauptachse (gestrichelte Gerade) gegenüber der $x$–Achse hängt ebenfalls von $σ_x$, $σ_y$ und $ρ_{xy}$ ab:

$$\alpha = {1}/{2} \cdot {\rm arctan } ( 2 \cdot \rho_{xy} \cdot \frac {\sigma_x \cdot \sigma_y}{\sigma_x^2 - \sigma_y^2}).$$

• Die (rote) Korrelationsgerade $y = K(x)$ einer Gaußschen 2D–Zufallsgröße liegt stets unterhalb der (blau gestrichelten) Ellipsenhauptachse.
• $K(x)$ kann auch aus dem Schnittpunkt der Höhenlinien und ihrer vertikalen Tangenten geometrisch konstruiert werden, wie es in obigen Skizzen in grüner Farbe angedeutet ist.

Zweidimensionale Verteilungsfunktion

$\text{Definition:}$  Die 2D-Verteilungsfunktion ist ebenso wie die 2D-WDF lediglich eine sinnvolle Erweiterung der eindimensionalen Verteilungsfunktion (VTF):

$$F_{xy}(r_{x},r_{y}) = {\rm Pr}\big [(x \le r_{x}) \cap (y \le r_{y}) \big ] .$$

Es ergeben sich folgende Gemeinsamkeiten und Unterschiede zwischen der 1D-VTF und der 2D-VTF:

• Der Funktionalzusammenhang zwischen zweidimensionaler WDF und zweidimensionaler VTF ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt:

$$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$

• Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $r_{x}$ und $r_{y}$ angeben:

$$f_{xy}(x,y)=\frac{{\rm d}^{\rm 2} F_{xy}(r_{x},r_{y})}{{\rm d} r_{x} \,\, {\rm d} r_{y}}\Bigg|_{\left.{r_{x}=x \atop {r_{y}=y}}\right.}.$$

• Bezüglich der Verteilungsfunktion $F_{xy}(r_{x}, r_{y})$ gelten folgende Grenzwerte:

$$F_{xy}(-\infty,-\infty) = 0,$$

$$F_{xy}(r_{\rm x},+\infty)=F_{x}(r_{x} ),$$

$$F_{xy}(+\infty,r_{y})=F_{y}(r_{y} ) ,$$

$$F_{xy}+\infty,+\infty) = 1.$$

• Im Grenzfall (unendlich große $r_{x}$ und $r_{y}$) ergibt sich demnach für die 2D-VTF der Wert $1$. Daraus erhält man die Normierungsbedingung für die 2D-Wahrscheinlichkeitsdichtefunktion:

$$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$

$\text{Fazit:}$  Beachten Sie den signifikanten Unterschied zwischen eindimensionalen und zweidimensionalen Zufallsgrößen:

• Bei eindimensionalen Zufallsgrößen ergibt die Fläche unter der WDF stets den Wert $1$.
• Bei zweidimensionalen Zufallsgrößen ist das WDF-Volumen immer gleich $1$.

Gaußsche 2D-WDF und 2D-VTF

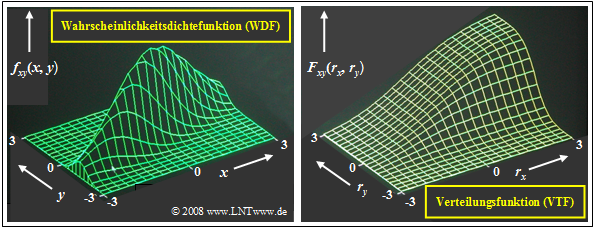
$\text{Beispiel 1:}$  Die beiden Grafiken zeigen

• die Wahrscheinlichkeitsdichtefunktion (links) und
• Verteilungsfunktion (rechts)

einer zweidimensionalen Gaußschen Zufallsgröße $(x, y)$ mit relativ starker positiver Korrelation der Einzelkomponenten:   $ρ_{xy} = 0.8$.

Wie bei den bisherigen Beispielen ist auch hier die 2D–Zufallsgröße in $x$–Richtung weiter ausgedehnt als in $y$–Richtung:   $σ_x = 2 · σ_y$.
Diese Darstellungen können wie folgt interpretiert werden:

• Die WDF ist vergleichbar mit einem Bergkamm, der sich von links unten nach rechts oben erstreckt.
• Das Maximum liegt bei $m_x = 0$ und $m_y = 0$. Das bedeutet, dass die die 2D–Zufallsgröße mittelwertfrei ist.
• Die 2D–VTF als das Integral in zwei Richtungen über die 2D–WDF steigt von links unten nach rechts oben von $0$ auf $1$ kontinuierlich an.

Das interaktive Applet WDF und VTF bei Gaußschen 2D-Zufallsgrößen erlaubt die Darstellung der zweidimensionalen Funktionen für beliebige Werte von $σ_x, \ σ_y$ und $ρ_{xy}$.

WDF und VTF bei statistisch unabhängigen Komponenten

Bei statistisch unabhängigen Komponenten $x$ und $y$ gilt für die Verbundwahrscheinlichkeit nach den elementaren Gesetzmäßigkeiten der Statistik, falls $x$ und $y$ wertkontinuierlich sind:

$${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap( y_{\rm 1}\le y\le y_{\rm 2})\big] ={\rm Pr} (x_{\rm 1}\le x \le x_{\rm 2}) \cdot {\rm Pr}(y_{\rm 1}\le y\le y_{\rm 2}) .$$

Hierfür kann bei unabhängigen Komponenten auch geschrieben werden:

$${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap(y_{\rm 1}\le y\le y_{\rm 2})\big] =\int _{x_{\rm 1}}^{x_{\rm 2}}f_{x}(x) \,{\rm d}x\cdot \int_{y_{\rm 1}}^{y_{\rm 2}} f_{y}(y) \, {\rm d}y.$$

$\text{Definition:}$  Daraus folgt, dass bei statistischer Unabhängigkeit folgende Bedingung bezüglich der 2D–WDF erfüllt sein muss:

$$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$

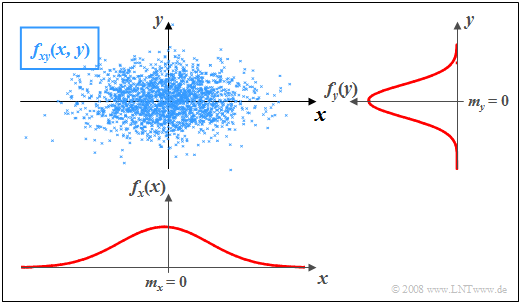
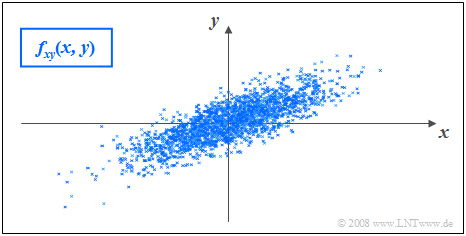
$\text{Beispiel 2:}$  In der Grafik sind die Momentanwerte einer zweidimensionalen Zufallsgröße als Punkte in der $(x, y)$-Ebene eingetragen.

• Bereiche mit vielen Punkten, die dementsprechend dunkel wirken, kennzeichnen große Werte der WDF $f_{xy}(x, y)$.
• Dagegen besitzt die Zufallsgröße $(x, y)$ in eher hellen Bereichen nur verhältnismäßig wenig Anteile.

Statistisch unabhängige Komponenten:   $f_{xy}(x,y)$, $f_{x}(x)$, $f_{y}(y)$

Die Grafik kann wie folgt interpretiert werden:

• Die Randwahrscheinlichkeitsdichten $f_{x}(x)$ und $f_{y}(y)$ lassen bereits erkennen, dass sowohl $x$ als auch $y$ gaußähnlich und mittelwertfrei sind, und dass die Zufallsgröße $x$ eine größere Streuung als $y$ aufweist.
• $f_{x}(x)$ und $f_{y}(y)$ liefern jedoch keine Informationen darüber, ob bei der Zufallsgröße $(x, y)$ statistische Bindungen bestehen oder nicht.
• Anhand der 2D-WDF $f_{xy}(x,y)$ erkennt man aber, dass es hier zwischen den beiden Komponenten $x$ und $y$ keine statistischen Bindungen gibt.
• Bei statistischer Unabhängigkeit liefert jeder Schnitt durch $f_{xy}(x, y)$ parallel zur $y$-Achse eine Funktion, die formgleich mit der Rand–WDF $f_{y}(y)$ ist.
• Ebenso sind alle Schnitte parallel zur $x$-Achse formgleich mit $f_{x}(x)$.

Diese Tatsache ist gleichbedeutend mit der Aussage, dass in diesem Beispiel die 2D-WDF $f_{xy}(x, y)$ als Produkt der beiden Randwahrscheinlichkeitsdichten dargestellt werden kann:   $f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$

WDF und VTF bei statistisch abhängigen Komponenten

Bestehen statistische Bindungen zwischen den Komponenten $x$ und $y$, so liefern unterschiedliche Schnitte parallel zur $x$– bzw. $y$–Achse jeweils unterschiedliche, nicht formgleiche Funktionen.

In diesem Fall lässt sich die Verbund–WDF natürlich auch nicht als Produkt der beiden (eindimensionalen) Randwahrscheinlichkeitsdichten beschreiben.

Statistisch abhängige Komponenten:   $f_{xy}(x,y)$, $f_{x}(x)$, $f_{y}(y)$

$\text{Beispiel 3:}$  Die Grafik zeigt die Momentanwerte einer zweidimensionalen Zufallsgröße in der $(x, y)$–Ebene, wobei nun im Gegensatz zum $\text{Beispiel 2}$ zwischen $x$ und $y$ statistische Bindungen bestehen.

• Die 2D–Zufallsgröße nimmt im blau eingezeichneten Parallelogramm alle Werte mit gleicher Wahrscheinlichkeit an.
• Außerhalb sind keine Werte möglich.

Man erkennt aus dieser Darstellung:

• Die Integration über $f_{xy}(x, y)$ parallel zu der $x$–Achse führt zur dreieckförmigen Randdichte $f_{y}(y)$, die Integration parallel zur $y$–Achse zur trapezförmigen WDF $f_{x}(x)$.
• Aus der 2D-WDF $f_{xy}(x, y)$ ist bereits zu erahnen, dass für jeden $x$–Wert im statistischen Mittel ein anderer $y$–Wert zu erwarten ist.
• Das bedeutet aber, dass hier die Komponenten $x$ und $y$ statistisch voneinander abhängen.

Erwartungswerte zweidimensionaler Zufallsgrößen

Ein Sonderfall der statistischen Abhängigkeit ist die Korrelation.

$\text{Definition:}$  Unter Korrelation versteht man eine lineare Abhängigkeit  zwischen den Einzelkomponenten $x$ und $y$.

• Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig.
• Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.

Zur quantitativen Erfassung der Korrelation verwendet man verschiedene Erwartungswerte der 2D-Zufallsgröße $(x, y)$.

Diese sind analog definiert zum eindimensionalen Fall

• gemäß Kapitel 2 (bei wertdiskreten Zufallsgrößen)
• bzw. Kapitel 3 (bei wertkontinuierlichen Zufallsgrößen):

$\text{Definition:}$  Für die (nichtzentrierten) Momente gilt die Beziehung:

$$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$

Die beiden linearen Mittelwerte sind somit $m_x = m_{10}$ und $m_y = m_{01}.$

$\text{Definition:}$  Die auf $m_x$ bzw. $m_y$ bezogenen Zentralmomente lauten:

$$\mu_{kl} = {\rm E}\big[(x-m_{x})\hspace{0.05cm}^k \cdot (y-m_{y})\hspace{0.05cm}^l\big] .$$

In dieser allgemein gültigen Definitionsgleichung sind die Varianzen $σ_x^2$ und $σ_y^2$ der zwei Einzelkomponenten durch $\mu_{20}$ bzw. $\mu_{02}$ mit enthalten.

$\text{Definition:}$  Besondere Bedeutung besitzt die Kovarianz $(k = l = 1)$, die ein Maß für die lineare statistische Abhängigkeit zwischen den Zufallsgrößen $x$ und $y$ ist:

$$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$

Im Folgenden bezeichnen wir die Kovarianz $\mu_{11}$ teilweise auch mit $\mu_{xy}$, falls sich die Kovarianz auf die Zufallsgrößen $x$ und $y$ bezieht. Die Kovarianz hängt wie folgt mit dem nichtzentrierten Moment $m_{11} = m_{xy} = {\rm E}\big[x · y\big]$ zusammen:

$$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$

Anmerkung:

• Diese Gleichung ist für die numerische Auswertung enorm vorteilhaft, da $m_{xy}$, $m_x$ und $m_y$ aus den Folgen $〈x_v〉$ und $〈y_v〉$ in einem Durchlauf gefunden werden können.
• Würde man dagegen die Kovarianz $\mu_{xy}$ entsprechend der oberen Definitionsgleichung berechnen, so müsste man in einem ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln und dann in einem zweiten Durchlauf den Erwartungswert ${\rm E}\big[(x - m_x) · (y - m_y)\big]$.

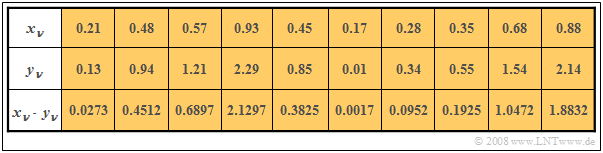
$\text{Beispiel 4:}$  In den beiden ersten Zeilen der folgenden Tabelle sind die jeweils ersten Elemente zweier Zufallsfolgen $〈x_ν〉$ und $〈y_ν〉$ eingetragen. In der letzten Zeile sind die jeweiligen Produkte $x_ν · y_ν$ angegeben.

Beispielhafte 2D-Erwartungswerte

Die Tabelle zeigt folgenden Sachverhalt:

• Durch Mittelung über die jeweils zehn Folgenelemente erhält man $m_x =0.5$, $m_y = 1$ und $m_{xy} = 0.69$.
• Daraus ergibt sich die Kovarianz zu $\mu_{xy} = 0.69 - 0.5 · 1 = 0.19.$
• Ohne Kenntnis der Gleichung $\mu_{xy} = m_{xy} - m_x · m_y$ hätte man zunächst im ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln müssen, um im zweiten Durchlauf die Kovarianz $\mu_{xy}$ als Erwartungswert des Produkts der mittelwertfreien Größen bestimmen zu können.

Korrelationskoeffizient

Bei statististischer Unabhängigkeit der beiden Komponenten $x$ und $y$ ist die Kovarianz $\mu_{xy} \equiv 0$. Dieser Fall wurde bereits im $\text{Beispiel 2}$ auf der Seite WDF und VTF bei statistisch unabhängigen Komponenten betrachtet.

• Das Ergebnis $\mu_{xy} = 0$ ist aber auch bei statistisch abhängigen Komponenten $x$ und $y$ möglich, nämlich dann, wenn diese unkorreliert, also linear unabhängig sind.
• Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $y=x^2.$

Man spricht von „vollständiger Korrelation”, wenn die (deterministische) Abhängigkeit zwischen $x$ und $y$ durch die Gleichung $y = K · x$ ausgedrückt wird. Dann ergibt sich für die Kovarianz:

• $\mu_{xy} = σ_x · σ_y$ bei positivem Wert von $K$,
• $\mu_{xy} = - σ_x · σ_y$ bei negativem $K$–Wert.

Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten.

$\text{Definition:}$  Der Korrelationskoeffizient ist der Quoient aus Kovarianz $\mu_{xy}$ und dem Produkt der Effektivwerte $σ_x$ und $σ_y$ der beiden Komponenten:

$$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$

Der Korrelationskoeffizient $\rho_{xy}$ weist folgende Eigenschaften auf:

• Aufgrund der Normierung gilt stets $-1 \le ρ_{xy} ≤ +1$.
• Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{xy} = 0$.
• Bei strenger linearer Abhängigkeit zwischen $x$ und $y$ ist $ρ_{xy}= ±1$   ⇒   vollständige Korrelation.
• Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $x$–Wert im statistischen Mittel auch $y$  größer ist als bei kleinerem $x$.
• Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $y$  mit steigendem $x$ im Mittel kleiner wird.

Gaußsche 2D-WDF mit Korrelation

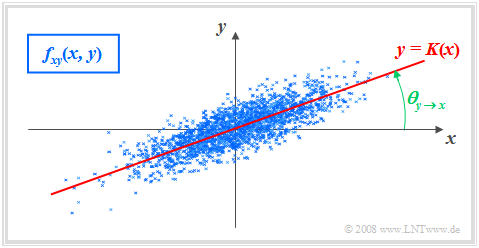
$\text{Beispiel 5:}$  Es gelten folgende Voraussetzungen:

• Die betrachteten Komponenten $x$ und $y$ besitzen jeweils eine gaußförmige WDF.
• Die beiden Streuungen sind unterschiedlich $(σ_y < σ_x)$.
• Der Korrelationskoeffizient beträgt $ρ_{xy} = 0.8$.

Im Unterschied zum Beispiel 2 mit statistisch unabhängigen Komponenten   ⇒   $ρ_{xy} = 0$ (trotz $σ_y < σ_x$) erkennt man, dass hier bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.

Korrelationsgerade

Gaußsche 2D-WDF mit Korrelationsgerade

$\text{Definition:}$  Als Korrelationsgerade bezeichnet man die Gerade $y = K(x)$ in der $(x, y)$–Ebene durch den „Mittelpunkt” $(m_x, m_y)$. Manchmal wird diese Gerade auch Regressionsgerade genannt.

Die Korrelationsgerade besitzt folgende Eigenschaften:

• Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Punkte gemittelt – ist minimal:

$$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$

• Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet:

$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$

Der Winkel, den die Korrelationsgerade zur $x$–Achse einnimmt, beträgt:

$$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}(\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$

Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von $y$ auf $x$ handelt.

• Die Regression in Gegenrichtung – also von $x$ auf $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in $x$–Richtung.

• Das interaktive Applet Korrelationskoeffizient und Regressionsgerade verdeutlicht, dass sich im Allgemeinen (falls $σ_y \ne σ_x$) für die Regression von $x$ auf $y$ ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird:

$$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}(\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$

Wahrscheinlichkeiten der Binomialverteilung

Hierfür gilt mit $μ = 0, \text{...}\ , I$:

$$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$

Der erste Term gibt hierbei die Anzahl der Kombinationen $(I \text{ über }\mu)$ an:

$${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$

Momente der Binomialverteilung

Für das Moment $k$-ter Ordnung einer binomialverteilten Zufallsgröße $z$ gilt:

$$m_k={\rm E}[z^k]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$

Daraus erhält man nach einigen Umformungen für

• den linearen Mittelwert:   $m_1 = I\cdot p,$
• den quadratischen Mittelwert:   $m_2 = (I^2-I)\cdot p^2+I\cdot p,$
• die Varianz bzw. die Streuung:   $\sigma^2 = {m_2-m_1^2} = {I \cdot p\cdot (1-p)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \sqrt{I \cdot p\cdot (1-p)}.$

Anwendungen der Binomialverteilung

Die Binomialverteilung findet in der Nachrichtentechnik ebenso wie in anderen Disziplinen mannigfaltige Anwendungen:

• Sie beschreibt die Verteilung von Ausschussstücken in der statistischen Qualitätskontrolle.
• Auch die per Simulation gewonnene Bitfehlerquote eines digitalen Übertragungssystems ist eigentlich eine binomialverteilte Zufallsgröße.
• Die Binomialverteilung erlaubt die Berechnung der Restfehlerwahrscheinlichkeit bei blockweiser Codierung, wie das folgende Beispiel zeigt.

$\text{Beispiel 1:}$  Überträgt man jeweils Blöcke von $I =5$ Binärsymbolen über einen Kanal, der

• mit der Wahrscheinlichkeit $p = 0.1$ ein Symbol verfälscht   ⇒   Zufallsgröße $e_i = 1$, und
• entsprechend mit der Wahrscheinlichkeit $1 - p = 0.9$ das Symbol unverfälscht überträgt   ⇒   Zufallsgröße $e_i = 0$,

so gilt für die neue Zufallsgröße $f$ („Fehler pro Block”):

$$f=\sum_{i=1}^{I}e_i.$$

Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen $\mu = 0$ (kein Symbol verfälscht) und $\mu = I = 5$ (alle fünf Symbole falsch) annehmen. Die Wahrscheinlichkeiten für $\mu$ Verfälschungen bezeichnen wir mit $p_μ = {\rm Pr}(f = \mu)$.

• Der Fall, dass alle fünf Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.9^{5} ≈ 0.5905$ ein. Dies ergibt sich auch aus der Binomialformel für $μ = 0$ unter Berücksichtigung der Definition $5\text{ über } 0 = 1$.
• Ein einziger Symbolfehler $(f = 1)$ tritt mit der Wahrscheinlichkeit $p_1 = 5\cdot 0.1\cdot 0.9^4\approx 0.3281$ auf. Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau $5\text{ über } 1 = 5$ Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und vier richtig übertragen werden müssen, wenn $f =1$ gelten soll.
• Für $f =2$ gibt es mehr Kombinationen, nämlich $5\text{ über } 2 = (5 \cdot 4)/(1 \cdot 2) = 10$, und man erhält $p_2 = 10\cdot 0.1^2\cdot 0.9^3\approx 0.0729$.

Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit $p_{\rm R} = 1-p_{\rm 0}-p_{\rm 1}-p_{\rm 2}\approx 0.85\%$. Eine zweite Berechnungsmöglichkeit wäre $p_{\rm R} = p_{3} + p_{4} + p_{5}$ mit der Näherung $p_{\rm R} \approx p_{3} = 0.81\%.$

Die mittlere Fehleranzahl in einem Block ist $m_f = 5 \cdot 0.1 = 0.5$. Die Varianz der Zufallsgröße $f$ beträgt $\sigma_f^2 = 5 \cdot 0.1 \cdot 0.9= 0.45$   ⇒   Streuung $\sigma_f \approx 0.671.$

Eigenschaften der Poissonverteilung

Die Poissonverteilung ist ein Grenzfall der Binomialverteilung, wobei

• zum einen von den Grenzübergängen $I → ∞$ und $p →$ 0 ausgegangen wird,
• zusätzlich vorausgesetzt ist, dass das Produkt $I · p = λ$ einen endlichen Wert besitzt.

Der Parameter $λ$ gibt die mittlere Anzahl der „Einsen” in einer festgelegten Zeiteinheit an und wird als die Rate bezeichnet.

Im Gegensatz zur Binomialverteilung ($0 ≤ μ ≤ I$) kann hier die Zufallsgröße beliebig große (ganzzahlige, nichtnegative) Werte annehmen, was bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer diskreten Verteilung.

Wahrscheinlichkeiten der Poissonverteilung

Berücksichtigt man die oben genannten Grenzübergänge in der Gleichung für die Wahrscheinlichkeiten der Binomialverteilung, so folgt für die Auftrittswahrscheinlichkeiten der poissonverteilten Zufallsgröße $z$:

$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$

Daraus erhält man nach einigen algebraischen Umformungen:

$$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$

Momente der Poissonverteilung

Bei der Poissonverteilung ergeben sich Mittelwert und Streuung direkt aus den entsprechenden Gleichungen der Binomialverteilung durch zweifache Grenzwertbildung:

$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty, \hspace{0.2cm} {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \hspace{0.2cm} I \cdot p= \lambda,$$

$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty, \hspace{0.2cm} {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \hspace{0.2cm} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$

Daraus ist zu erkennen, dass bei der Poissonverteilung stets $\sigma^2 = m_1 = \lambda$ ist. Dagegen gilt bei der Binomialverteilung immer $\sigma^2 < m_1$.

Momente der Poissonverteilung

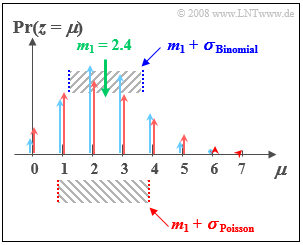
$\text{Beispiel 2:}$  Wir vergleichen nun die Binomialverteilung mit den Parametern $I =6$ und $p = 0.4$ und die Poissonverteilung mit $λ = 2.4$:

• Beide Verteilungen besitzen genau den gleichen Mittelwert $m_1 = 2.4$.
• Bei der Poissonverteilung (im Bild rot markiert) beträgt die Streuung $σ ≈ 1.55$.
• Bei der (blauen) Binomialverteilung ist die Standardabweichung nur $σ = 1.2$.

Anwendungen der Poissonverteilung

Die Poissonverteilung ist das Ergebnis eines so genannten Poissonprozesses. Ein solcher dient häufig als Modell für Folgen von Ereignissen, die zu zufälligen Zeitpunkten eintreten können. Beispiele für derartige Ereignisse sind

• der Ausfall von Geräten – eine wichtige Aufgabenstellung in der Zuverlässigkeitstheorie,
• das Schrotrauschen bei der optischen Übertragung, und
• der Beginn von Telefongesprächen in einer Vermittlungsstelle („Verkehrstheorie”).

$\text{Beispiel 3:}$  Gehen bei einer Vermittlungsstelle im Langzeitmittel neunzig Vermittlungswünsche pro Minute ein (also $λ = 1.5 \text{ pro Sekunde}$), so lauten die Wahrscheinlichkeiten $p_{\mu}$, dass in einem beliebigen Zeitraum von einer Sekunde genau $\mu$ Belegungen auftreten:

$$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$

Es ergeben sich die Zahlenwerte $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, usw.

Daraus lassen sich weitere Kenngrößen ableiten:

• Die Abstand $τ$ zwischen zwei Vermittlungswünschen genügt der Exponentialverteilung.
• Die mittlere Zeitspanne zwischen Vermittlungswünschen beträgt ${\rm E}[τ] = 1/λ ≈ 0.667 \ \rm s$.

Gegenüberstellung Binomialverteilung vs. Poissonverteilung

Hier sollen die Gemeinsamkeiten und die Unterschiede zwischen binomial- und poissonverteilten Zufallsgrößen herausgearbeitet werden.

Binomialverteilung vs. Poissonverteilung

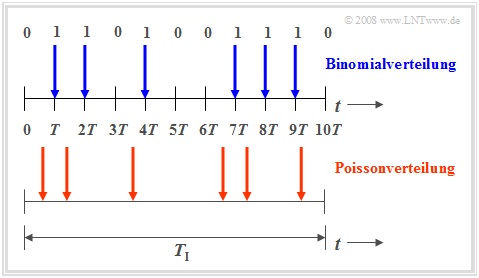
Die Binomialverteilung ist zur Beschreibung solcher stochastischer Ereignisse geeignet, die durch einen festen Takt $T$ gekennzeichnet sind. Beispielsweise beträgt bei ISDN (Integrated Services Digital Network) mit $64 \ \rm kbit/s$ die Taktzeit $T \approx 15.6 \ \rm µ s$.

• Nur in diesem Zeitraster treten binäre Ereignisse auf. Solche Ereignisse sind beispielsweise die fehlerfreie $(e_i = 0)$ oder fehlerhafte $(e_i = 1)$ Übertragung einzelner Symbole.
• Die Binomialverteilung ermöglicht nun statistische Aussagen über die Anzahl der in einem längeren Zeitintervall $T_{\rm I} = I · T$ zu erwartenden Übertragungsfehler entsprechend des skizzierten Zeitdiagramms (blau markierte Zeitpunkte).
• Für sehr große Werte von $I$ und gleichzeitig sehr kleine Werte von $p$ kann die Binomialverteilung durch die Poissonverteilung mit $\lambda = I \cdot p$ angenähert werden.
• Ist gleichzeitig das Produkt $I · p \gg 1$, so geht nach dem Grenzwertsatz von de Moivre-Laplace die Poissonverteilung (und damit auch die Binomialverteilung) in eine diskrete Gaußverteilung über.

Die Poissonverteilung macht ebenfalls Aussagen über die Anzahl eintretender Binärereignisse in einem endlichen Zeitintervall.

Geht man hierbei vom gleichen Betrachtungszeitraum $T_{\rm I}$ aus und vergrößert die Anzahl $I$ der Teilintervalle immer mehr, so wird die Taktzeit $T,$ zu der jeweils ein neues Binärereignis ($0$ oder $1$) eintreten kann, immer kleiner. Im Grenzfall geht $T$ gegen Null. Das heißt:

• Bei der Poissonverteilung sind die binären Ereignisse nicht nur zu diskreten, durch ein Zeitraster vorgegebenen Zeitpunkten möglich, sondern jederzeit. Das untere Zeitdiagramm verdeutlicht diesen Sachverhalt.
• Um im Mittel während der Zeit $T_{\rm I}$ genau so viele „Einsen” wie bei der Binomialverteilung zu erhalten (im Beispiel: sechs), muss allerdings die auf das infinitesimal kleine Zeitintervall $T$ bezogene charakteristische Wahrscheinlichkeit $p = {\rm Pr}( e_i = 1)$ gegen Null tendieren.

Versuchsdurchführung

• Wählen Sie zunächst die Nummer 1 ... 6 der zu bearbeitenden Aufgabe.
• Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
• Lösung nach Drücken von „Hide solution”.
• Aufgabenstellung und Lösung in Englisch.

Die Nummer 0 entspricht einem „Reset”:

• Gleiche Einstellung wie beim Programmstart.
• Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.

In der folgenden Beschreibung bedeutet

• Blau:   Verteilungsfunktion 1 (im Applet blau markiert),
• Rot:     Verteilungsfunktion 2 (im Applet rot markiert).

(1)  Setzen Sie Blau: Binomialverteilung $(I=5, \ p=0.4)$ und Rot: Binomialverteilung $(I=10, \ p=0.2)$.

Wie lauten die Wahrscheinlichkeiten ${\rm Pr}(z=0)$ und ${\rm Pr}(z=1)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blau: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$

$\hspace{1.85cm}\text{Rot: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$

(2)  Es gelten weiter die Einstellungen von (1). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(3 \le z \le 5)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Es gilt }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, oder } {\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$.

$\hspace{1.85cm}\text{Blau: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$

$\hspace{1.85cm}\text{Rot: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158.$

(3)  Es gelten weiter die Einstellungen von (1). Wie unterscheiden sich der Mittelwert $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2; $

$\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 < \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$

(4)  Setzen Sie Blau: Binomialverteilung $(I=15, p=0.3)$ und Rot: Poissonverteilung $(\lambda=4.5)$.

Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\hspace{0.15cm}\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$;

$\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;

(5)  Es gelten die Einstellungen von (4). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(z \gt 10)$ und ${\rm Pr}(z \gt 15)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0 \ {\rm (exakt)}$.

$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0 \ ( \approx 0)$

$\hspace{1.85cm} \text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \ge {\rm Pr}(z = 16) = \lambda^{16}/{16!}\approx 2 \cdot 10^{-22}$.

(6)  Es gelten weiter die Einstellungen von (4). Mit welchen Parametern ergeben sich symmetrische Verteilungen um $m_1$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomialverung mit }p = 0.5\text{: }p_\mu = {\rm Pr}(z = \mu)\text{ symmetrisch um } m_1 = I/2 = 7.5 \ ⇒ \ p_μ = p_{I–μ}\ ⇒ \ p_8 = p_7, \ p_9 = p_6, \text{usw.}$

$\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$

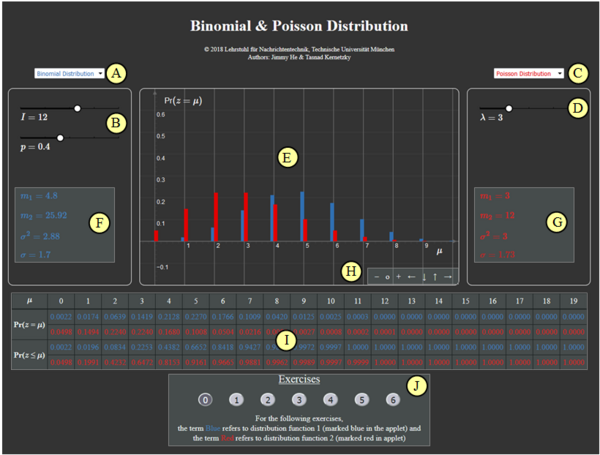
Zur Handhabung des Applets

    (A)     Vorauswahl für blauen Parametersatz

    (B)     Parametereingabe $I$ und $p$ per Slider

    (C)     Vorauswahl für roten Parametersatz

    (D)     Parametereingabe $\lambda$ per Slider

    (E)     Graphische Darstellung der Verteilungen

    (F)     Momentenausgabe für blauen Parametersatz

    (G)     Momentenausgabe für roten Parametersatz

    (H)     Variation der grafischen Darstellung

$\hspace{1.5cm}$„$+$” (Vergrößern),

$\hspace{1.5cm}$ „$-$” (Verkleinern)

$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)

$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.

    ( I )     Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$

    (J)     Bereich für die Versuchsdurchführung

Andere Möglichkeiten zur Variation der grafischen Darstellung:

• Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
• Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

• Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
• 2018 wurde das Programm von Jimmy He (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Applet in neuem Tab öffnen