Aufgabe 2.6: Zyklisches Präfix: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
|||
| (9 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
}} | }} | ||
| − | [[Datei:P_ID1982__Bei_A_2_6.png|right|frame|DSL/DMT mit zyklischem Präfix]] | + | [[Datei:P_ID1982__Bei_A_2_6.png|right|frame|$\rm DSL/DMT$ mit <br>zyklischem Präfix]] |
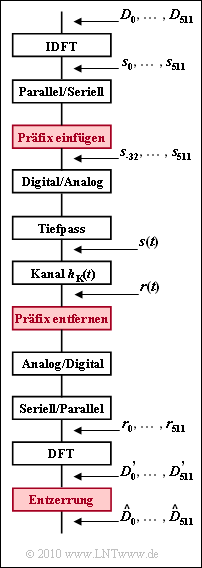
| + | Ein wesentlicher Vorteil von $\rm DSL/DMT$ ist die einfache Entzerrung von Kanalverzerrungen durch die Einfügung eines Guard–Intervalls und eines zyklischen Präfix. Die Grafik zeigt ein vereinfachendes Blockschaltbild, wobei die zur Entzerrung des Kanalfrequenzgangs | ||
| + | :$$H_{\rm K}(f) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm K}(t)$$ | ||
| + | erforderlichen Komponenten rot hervorgehoben sind. | ||
| + | |||
| + | Für den $\rm ADSL/DMT$–Downstream gelten folgende Parameter: | ||
| + | |||
| + | *Mit jedem Rahmen werden die Subkanäle $k = 64$, ... , $255$ bei den Trägerfrequenzen $f_k = k \cdot f_0$ mit den QAM–Symbolen $D_k$ belegt. Wegen der Reservierung der untersten Frequenzen für ISDN und für den Upstream gilt $D_0 =$ ... $= D_{63} = 0$. | ||
| + | |||
| + | *Die Grundfrequenz ist zu $f_0 = 4.3125 \ \rm kHz$ gewählt und die Rahmendauer beträgt $T = 1/f_0 \approx 232 \ {\rm µ s}$. Diese Werte ergeben sich aus der Forderung, dass pro Sekunde $4000$ Rahmen übertragen werden sollen und nach jedem $68$–ten Rahmen ein Synchronisationsrahmen eingefügt wird. | ||
| + | |||
| + | *Nach Belegung der oberen Koeffizienten $(k = 257$, ... , $448)$ gemäß $D_k = D_{512-k}^{\ast}$ wird der gesamte Block $D_0$, ... , $D_{511}$ einer ''Inversen Diskreten Fouriertransformation'' $\rm (IDFT)$ zugeführt. Die Zeitkoeffizienten sind dann $s_0$, ... , $s_{511}$. | ||
| + | |||
| + | *Um Impulsinterferenzen – auch ''Inter–Symbol–Interferenzen'' $\rm (ISI)$ genannt – zwischen benachbarten Rahmen zu vermeiden, wird zwischen zwei Rahmen ein Schutzabstand („Guard–Intervall”) der Dauer $T_{\rm G}$ eingefügt. Der Rahmenabstand muss dabei mindestens so groß sein wie die „Länge” $T_{\rm K}$ der Impulsantwort. | ||
| + | |||
| + | *Zudem werden die IDFT–Ausgangswerte $(s_{480}$, ... , $s_{511})$ dupliziert, als $(s_{-32}$, ... , $s_{-1})$ dem Ausgangsvektor $(s_0$, ... , $s_{511})$ vorangestellt und im Guard–Intervall übertragen. Man nennt dies das „zyklische Präfix”. Somit stören sich auch die Subträger eines Rahmens nicht, das heißt, es gibt nicht nur keine $\rm ISI$, sondern auch keine Inter–Carrier–Interferenzen $\rm (ICI)$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Beispiele_von_Nachrichtensystemen/Verfahren_zur_Senkung_der_Bitfehlerrate_bei_DSL|Verfahren zur Senkung der Bitfehlerrate bei DSL]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Beispiele_von_Nachrichtensystemen/Verfahren_zur_Senkung_der_Bitfehlerrate_bei_DSL#Einf.C3.BCgen_von_Guard.E2.80.93Intervall_und_zyklischem_Pr.C3.A4fix|Einfügen von Guard–Intervall und zyklischem Präfix]]. | ||
| + | *Im Fragebogen bezeichnet $s_k(t)$ den (zeitkontinuierlichen) Signalverlauf, wenn allein der Koeffizient $D_k$ des Trägers bei $f_k = k \cdot f_0$ von Null verschieden ist. | ||
| + | |||
| Zeile 14: | Zeile 43: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| + | |||
| + | {Wie groß ist die Dauer $T_{\rm G}$ des Guard–Intervalls zu wählen? | ||
| + | |type="{}"} | ||
| + | $T_{\rm G} \ = \ ${ 14.5 3% } $ \ \rm µ s$ | ||
| + | |||
| + | |||
| + | {Welche Ausdehnung $(T_{\rm K, \ max} )$ darf die Kanalimpulsantwort $h_{\rm K}(t)$ haben, damit es keine Intersymbolinterferenzen gibt? | ||
| + | |type="{}"} | ||
| + | $T_{\rm K, \ max} \ = \ ${ 14.5 3% } $ \ \rm µ s$ | ||
| + | |||
| + | {Welche Eigenschaften besitzt das DMT–System mit zyklischem Präfix? Der Einfluss des Rauschens soll hier unberücksichtigt bleiben. | ||
| + | |type="()"} | ||
| + | - Alle Spektralkoeffizienten nach der DFT $(D_k\hspace{0.01cm}')$ sind gleich $D_k$. | ||
| + | + Die Koeffizienten nach Entzerrung $(\hat{D}_k)$ sind gleich $D_k$. | ||
| + | - Das Guard–Intervall hat keine Auswirkung auf die Datenrate. | ||
| + | |||
| + | |||
| + | {Was wäre, wenn man das Guard–Intervall unbelegt lässt? | ||
| + | |type="()"} | ||
| + | - Das würde nichts verbessern. | ||
| + | + Daten verschiedener Rahmen stören sich nicht gegenseitig. | ||
| + | - Daten innerhalb eines Rahmens stören sich nicht gegenseitig. | ||
| + | |||
| + | |||
| + | |||
| + | {Auf welchem Prinzip beruht das zyklische Präfix? | ||
| + | |type="[]"} | ||
| + | + Der Einfluss von $h_K(t)$ wird auf den Bereich $t < 0$ begrenzt. | ||
| + | + Für $0 ≤ t ≤ T$ stellt $s_k(t)$ eine harmonische Schwingung dar. | ||
| + | - $h_{\rm K}(t)$ hat keinen Einfluss auf Betrag und Phase von $s_k(t)$. | ||
| Zeile 23: | Zeile 82: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Innerhalb des Guard–Intervalls müssen beim Sender $32$ zusätzliche Abtastwerte $s_{-32}$, ... , $s_{-1}$ eingefügt werden. Damit gilt: |
| + | :$$T_{\rm G} = \frac{32}{512} \cdot T = \frac{232\,{\rm µ s}}{16} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s} }\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Intersymbolinterferenzen (ISI) und Intercarrierinterferenzen (ICI) werden vermieden, so lange die Länge $T_{\rm K}$ der Kanalimpulsantwort nicht größer ist als die Länge $T_{\rm G}$ des Guard–Intervalls: | ||
| + | :$$T_{\rm K,\hspace{0.08cm} max} \le T_{\rm G} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Richtig ist der <u>Lösungsvorschlag 2</u>. | ||
| + | *Für die Ausgangskoeffizienten der DFT gilt im rauschfreien Fall: | ||
| + | :$$D_k\hspace{0.01cm}' = D_k \cdot H_{\rm K} ( f = f_k), \hspace{0.2cm} f_k = k \cdot f_0 \hspace{0.05cm}.$$ | ||
| + | *Die einzelnen Subkanäle können einzeln durch Multiplikation mit $H_{\rm K}^{-1}(f = f_k)$ entzerrt werden. Damit gilt für alle $k = 1$, ... , $K$: | ||
| + | :$$\hat{D}_k = D_k \hspace{0.05cm}.$$ | ||
| + | *Aussage 3 ist falsch: Die Rate ist vielmehr um den Faktor $T/(T + T_{\rm G}) = 16/17$ geringer als ohne Guard–Intervall und zyklischem Präfix. | ||
| + | *Dieser geringe Verlust wird aber gerne in Kauf genommen, da die einfache Entzerrung diesen Nachteil mehr als ausgleicht. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Richtig ist hier nur der <u>Lösungsvorschlag 2</u>: | ||
| + | *Nicht verhindert würden dadurch so genannte Inter–Carrier–Interferenzen, das heißt, die Subträger eines Rahmens wären dann nicht mehr orthogonal zueinander, da die Faltung der zeitlich auf $T$ begrenzten harmonischen Schwingung mit der Impulsantwort keine si–Funktion ergibt, wie dies bei [[Beispiele_von_Nachrichtensystemen/xDSL_als_Übertragungstechnik#Grundlagen_von_DMT_.E2.80.93_Discrete_Multitone_Transmission|idealem Kanal]] der Fall ist. | ||
| + | *Damit beeinflusst der Koeffizient $D_k$ bei $k \cdot f_0$ auch die Spektralwerte bei $\kappa \cdot f_0$ in der Umgebung $(\kappa \neq k)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Richtig sind die <u>Lösungsvorschläge 1 und 2</u>: | ||
| + | *Betrag und Phase von $s_k(t)$ wird sehr wohl durch $h_{\rm K}(t)$ verändert, und zwar entsprechend dem Wert $H_{\rm K}(f = f_k)$ des Frequenzgangs. | ||
| + | *Durch den Entzerrer auf der Empfängerseite lässt sich dieser Fehler aber in einfacher Weise (und unabhängig von den anderen Subkanälen) korrigieren. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Zeile 29: | Zeile 114: | ||
| − | [[Category:Aufgaben zu Beispiele von Nachrichtensystemen|^2.4 Verfahren zur Senkung | + | [[Category:Aufgaben zu Beispiele von Nachrichtensystemen|^2.4 Verfahren zur BER–Senkung bei DSL |
^]] | ^]] | ||
Aktuelle Version vom 5. August 2019, 16:26 Uhr
Ein wesentlicher Vorteil von $\rm DSL/DMT$ ist die einfache Entzerrung von Kanalverzerrungen durch die Einfügung eines Guard–Intervalls und eines zyklischen Präfix. Die Grafik zeigt ein vereinfachendes Blockschaltbild, wobei die zur Entzerrung des Kanalfrequenzgangs
- $$H_{\rm K}(f) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm K}(t)$$
erforderlichen Komponenten rot hervorgehoben sind.
Für den $\rm ADSL/DMT$–Downstream gelten folgende Parameter:
- Mit jedem Rahmen werden die Subkanäle $k = 64$, ... , $255$ bei den Trägerfrequenzen $f_k = k \cdot f_0$ mit den QAM–Symbolen $D_k$ belegt. Wegen der Reservierung der untersten Frequenzen für ISDN und für den Upstream gilt $D_0 =$ ... $= D_{63} = 0$.
- Die Grundfrequenz ist zu $f_0 = 4.3125 \ \rm kHz$ gewählt und die Rahmendauer beträgt $T = 1/f_0 \approx 232 \ {\rm µ s}$. Diese Werte ergeben sich aus der Forderung, dass pro Sekunde $4000$ Rahmen übertragen werden sollen und nach jedem $68$–ten Rahmen ein Synchronisationsrahmen eingefügt wird.
- Nach Belegung der oberen Koeffizienten $(k = 257$, ... , $448)$ gemäß $D_k = D_{512-k}^{\ast}$ wird der gesamte Block $D_0$, ... , $D_{511}$ einer Inversen Diskreten Fouriertransformation $\rm (IDFT)$ zugeführt. Die Zeitkoeffizienten sind dann $s_0$, ... , $s_{511}$.
- Um Impulsinterferenzen – auch Inter–Symbol–Interferenzen $\rm (ISI)$ genannt – zwischen benachbarten Rahmen zu vermeiden, wird zwischen zwei Rahmen ein Schutzabstand („Guard–Intervall”) der Dauer $T_{\rm G}$ eingefügt. Der Rahmenabstand muss dabei mindestens so groß sein wie die „Länge” $T_{\rm K}$ der Impulsantwort.
- Zudem werden die IDFT–Ausgangswerte $(s_{480}$, ... , $s_{511})$ dupliziert, als $(s_{-32}$, ... , $s_{-1})$ dem Ausgangsvektor $(s_0$, ... , $s_{511})$ vorangestellt und im Guard–Intervall übertragen. Man nennt dies das „zyklische Präfix”. Somit stören sich auch die Subträger eines Rahmens nicht, das heißt, es gibt nicht nur keine $\rm ISI$, sondern auch keine Inter–Carrier–Interferenzen $\rm (ICI)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Verfahren zur Senkung der Bitfehlerrate bei DSL.
- Bezug genommen wird insbesondere auf die Seite Einfügen von Guard–Intervall und zyklischem Präfix.
- Im Fragebogen bezeichnet $s_k(t)$ den (zeitkontinuierlichen) Signalverlauf, wenn allein der Koeffizient $D_k$ des Trägers bei $f_k = k \cdot f_0$ von Null verschieden ist.
Fragebogen
Musterlösung
- $$T_{\rm G} = \frac{32}{512} \cdot T = \frac{232\,{\rm µ s}}{16} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s} }\hspace{0.05cm}.$$
(2) Intersymbolinterferenzen (ISI) und Intercarrierinterferenzen (ICI) werden vermieden, so lange die Länge $T_{\rm K}$ der Kanalimpulsantwort nicht größer ist als die Länge $T_{\rm G}$ des Guard–Intervalls:
- $$T_{\rm K,\hspace{0.08cm} max} \le T_{\rm G} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s}} \hspace{0.05cm}.$$
(3) Richtig ist der Lösungsvorschlag 2.
- Für die Ausgangskoeffizienten der DFT gilt im rauschfreien Fall:
- $$D_k\hspace{0.01cm}' = D_k \cdot H_{\rm K} ( f = f_k), \hspace{0.2cm} f_k = k \cdot f_0 \hspace{0.05cm}.$$
- Die einzelnen Subkanäle können einzeln durch Multiplikation mit $H_{\rm K}^{-1}(f = f_k)$ entzerrt werden. Damit gilt für alle $k = 1$, ... , $K$:
- $$\hat{D}_k = D_k \hspace{0.05cm}.$$
- Aussage 3 ist falsch: Die Rate ist vielmehr um den Faktor $T/(T + T_{\rm G}) = 16/17$ geringer als ohne Guard–Intervall und zyklischem Präfix.
- Dieser geringe Verlust wird aber gerne in Kauf genommen, da die einfache Entzerrung diesen Nachteil mehr als ausgleicht.
(4) Richtig ist hier nur der Lösungsvorschlag 2:
- Nicht verhindert würden dadurch so genannte Inter–Carrier–Interferenzen, das heißt, die Subträger eines Rahmens wären dann nicht mehr orthogonal zueinander, da die Faltung der zeitlich auf $T$ begrenzten harmonischen Schwingung mit der Impulsantwort keine si–Funktion ergibt, wie dies bei idealem Kanal der Fall ist.
- Damit beeinflusst der Koeffizient $D_k$ bei $k \cdot f_0$ auch die Spektralwerte bei $\kappa \cdot f_0$ in der Umgebung $(\kappa \neq k)$.
(5) Richtig sind die Lösungsvorschläge 1 und 2:
- Betrag und Phase von $s_k(t)$ wird sehr wohl durch $h_{\rm K}(t)$ verändert, und zwar entsprechend dem Wert $H_{\rm K}(f = f_k)$ des Frequenzgangs.
- Durch den Entzerrer auf der Empfängerseite lässt sich dieser Fehler aber in einfacher Weise (und unabhängig von den anderen Subkanälen) korrigieren.