Aufgaben:Aufgabe 5.9: Minimierung des MQF: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID652__Sto_A_5_9.png|right|frame|Leistungsdichtespektren beim Wiener-Filter ]] | + | [[Datei:P_ID652__Sto_A_5_9.png|right|frame|Leistungsdichtespektren <br>beim Wiener-Filter ]] |
| − | Gegeben ist ein stochastisches Nutzsignal $s(t)$, von dem nur das Leistungsdichtespektrum (LDS) bekannt ist: | + | Gegeben ist ein stochastisches Nutzsignal $s(t)$, von dem nur das Leistungsdichtespektrum (LDS) bekannt ist: |
:$${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$ | :$${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$ | ||
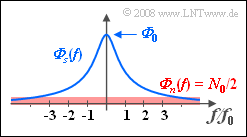
| − | Dieses Leistungsdichtespektrum ${\it \Phi} _s (f)$ ist in der nebenstehenden Grafik blau dargestellt. | + | Dieses Leistungsdichtespektrum ${\it \Phi} _s (f)$ ist in der nebenstehenden Grafik blau dargestellt. |
| − | *Die mittlere Leistung von $s(t)$ ergibt sich durch Integration über das Leistungsdichtespektrum: | + | *Die mittlere Leistung von $s(t)$ ergibt sich durch Integration über das Leistungsdichtespektrum: |
:$$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$ | :$$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$ | ||
| − | *Additiv überlagert ist dem Nutzsignal $s(t)$ Weißes Rauschen mit der Rauschleistungsdichte ${\it \Phi}_n(f) = N_0/2.$ | + | *Additiv überlagert ist dem Nutzsignal $s(t)$ Weißes Rauschen $n(t)$ mit der Rauschleistungsdichte ${\it \Phi}_n(f) = N_0/2.$ |
| − | *Als Abkürzung verwenden wir $Q = 2 \cdot {\it \Phi}_0/N_0$, wobei $Q$ als „Qualität” interpretiert werden könnte. | + | *Als Abkürzung verwenden wir $Q = 2 \cdot {\it \Phi}_0/N_0$, wobei $Q$ als „Qualität” interpretiert werden könnte. |
| − | *Zu beachten ist, dass $Q$ kein Signal–zu–Rauschleistungsverhältnis darstellt. | + | *Zu beachten ist, dass $Q$ kein Signal–zu–Rauschleistungsverhältnis darstellt. |
| − | In dieser Aufgabe soll der Frequenzgang $H(f)$ eines Filters ermittelt werden, das den mittleren quadratischen Fehler $\rm (MQF)$ zwischen dem Nutzsignal $s(t)$ und dem Filterausgangssignal $d(t)$ minimiert: | + | In dieser Aufgabe soll der Frequenzgang $H(f)$ eines Filters ermittelt werden, das den mittleren quadratischen Fehler $\rm (MQF)$ zwischen dem Nutzsignal $s(t)$ und dem Filterausgangssignal $d(t)$ minimiert: |
:$${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$ | :$${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$ | ||
| + | |||
| + | |||
| Zeile 23: | Zeile 25: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Wiener–Kolmogorow–Filter|Wiener–Kolmogorow–Filter]]. | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Wiener–Kolmogorow–Filter|Wiener–Kolmogorow–Filter]]. |
*Zur Lösung vorgegeben wird das folgende unbestimmte Integral: | *Zur Lösung vorgegeben wird das folgende unbestimmte Integral: | ||
| Zeile 36: | Zeile 38: | ||
{Welche der folgenden Aussagen sind zutreffend? | {Welche der folgenden Aussagen sind zutreffend? | ||
|type="[]"} | |type="[]"} | ||
| − | - $H(f)$ ist ein Gaußtiefpass. | + | - $H(f)$ ist ein Gaußtiefpass. |
| − | - $H(f)$ stellt ein Matched–Filter dar. | + | - $H(f)$ stellt ein Matched–Filter dar. |
| − | + $H(f)$ ist ein Wiener–Kolmogorow–Filter. | + | + $H(f)$ ist ein Wiener–Kolmogorow–Filter. |
| − | {Bestimmen Sie den Frequenzgang $H(f)$ des hierfür optimalen Filters. | + | {Bestimmen Sie den Frequenzgang $H(f)$ des hierfür optimalen Filters. Welche Werte ergeben sich mit $Q = 3$ bei $f = 0$ und $f = 2f_0$? |
|type="{}"} | |type="{}"} | ||
$H(f = 0) \ = \ $ { 0.75 3% } | $H(f = 0) \ = \ $ { 0.75 3% } | ||
| Zeile 47: | Zeile 49: | ||
| − | {Es gelte weiter $Q = 3$. Berechnen Sie den mittleren quadratischen Fehler $(\rm MQF)$ bezogen auf $P_s$ für das bestmögliche Filter. | + | {Es gelte weiter $Q = 3$. Berechnen Sie den mittleren quadratischen Fehler $(\rm MQF)$ bezogen auf $P_s$ für das bestmögliche Filter. |
|type="{}"} | |type="{}"} | ||
${\rm MQF}/P_s \ = \ $ { 0.5 3% } | ${\rm MQF}/P_s \ = \ $ { 0.5 3% } | ||
| − | {Wie groß muss der „Qualitätsfaktor” $Q$ mindestens gewählt werden, damit für den Quotienten der Wert ${\rm MQF}/P_s = 0.1$ erreicht werden kann? | + | {Wie groß muss der „Qualitätsfaktor” $Q$ mindestens gewählt werden, damit für den Quotienten der Wert ${\rm MQF}/P_s = 0.1$ erreicht werden kann? |
|type="{}"} | |type="{}"} | ||
$Q_\text{min} \ = \ $ { 99 3% } | $Q_\text{min} \ = \ $ { 99 3% } | ||
| Zeile 59: | Zeile 61: | ||
{Welche der folgenden Aussagen sind zutreffend? | {Welche der folgenden Aussagen sind zutreffend? | ||
|type="[]"} | |type="[]"} | ||
| − | - Ein formgleiches Filter $H(f) = K \cdot H_{\rm WF}(f)$ führt zum gleichen Ergebnis. | + | - Ein formgleiches Filter $H(f) = K \cdot H_{\rm WF}(f)$ führt zum gleichen Ergebnis. |
| − | + Das Ausgangssignal $d(t)$ enthält bei größerem $Q$ mehr höherfrequente Anteile. | + | + Das Ausgangssignal $d(t)$ enthält bei größerem $Q$ mehr höherfrequente Anteile. |
Version vom 10. Dezember 2019, 12:06 Uhr
Gegeben ist ein stochastisches Nutzsignal $s(t)$, von dem nur das Leistungsdichtespektrum (LDS) bekannt ist:
- $${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$
Dieses Leistungsdichtespektrum ${\it \Phi} _s (f)$ ist in der nebenstehenden Grafik blau dargestellt.
- Die mittlere Leistung von $s(t)$ ergibt sich durch Integration über das Leistungsdichtespektrum:
- $$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$
- Additiv überlagert ist dem Nutzsignal $s(t)$ Weißes Rauschen $n(t)$ mit der Rauschleistungsdichte ${\it \Phi}_n(f) = N_0/2.$
- Als Abkürzung verwenden wir $Q = 2 \cdot {\it \Phi}_0/N_0$, wobei $Q$ als „Qualität” interpretiert werden könnte.
- Zu beachten ist, dass $Q$ kein Signal–zu–Rauschleistungsverhältnis darstellt.
In dieser Aufgabe soll der Frequenzgang $H(f)$ eines Filters ermittelt werden, das den mittleren quadratischen Fehler $\rm (MQF)$ zwischen dem Nutzsignal $s(t)$ und dem Filterausgangssignal $d(t)$ minimiert:
- $${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Wiener–Kolmogorow–Filter.
- Zur Lösung vorgegeben wird das folgende unbestimmte Integral:
- $$\int {\frac{1}{a^2 + x^2 }} \, {\rm{d}}x ={1}/{a} \cdot \arctan \left( {{x}/{a}} \right).$$
Fragebogen
Musterlösung
- Die Aufgabenstellung ⇒ „Minimierung des mittleren quadratischen Fehlers” weist bereits auf das Filter nach Wiener–Kolmogorow hin.
- Das Matched–Filter verwendet man dagegen, um die Signalenergie zu bündeln und dadurch für einen vorgegebenen Zeitpunkt das S/N–Verhältnis zu maximieren.
(2) Für den optimalen Frequenzgang gilt nach Wiener und Kolmogorow allgemein:
- $$H(f) = H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$
- Mit den gegebenen Leistungsdichtespektren kann hierfür auch geschrieben werden:
- $$H(f) = \frac{1}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} = \frac{1}{{1 + {1}/{Q}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}}.$$
- Mit $Q = 3$ folgt daraus:
- $$H( {f = 0} ) = \frac{1}{{1 + {1}/{Q}}} = \frac{Q}{Q + 1} \hspace{0.15cm}\underline {= 0.75},$$
- $$H( {f = 2f_0 } ) = \frac{1}{{1 + {5}/{Q}}} = \frac{Q}{Q + 5} \hspace{0.15cm}\underline {= 0.375}.$$
(3) Für das in der Teilaufgabe (2) berechnete Filter gilt unter Berücksichtigung der Symmetrie:
- $${\rm{MQF = }}\int_{-\infty}^{+\infty} H(f) \cdot {\it \Phi} _n (f) \,\, {\rm{d}}f = \int_{0}^{+\infty} \frac{N_0}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} \,\, {\rm{d}}f .$$
- Hierfür kann mit $Q = 2 \cdot {\it \Phi}_0/N_0$ und $a^2 = Q + 1$ auch geschrieben werden:
- $${\rm{MQF = }}\int_0^\infty {\frac{{2{\it \Phi} _0 }}{{ Q+1 + ( {f/f_0 })^2 }}} \,\, {\rm{d}}f = 2{\it \Phi} _0 \cdot f_0 \int_0^\infty {\frac{1}{a^2 + x^2 }}\,\, {\rm{d}}x.$$
- Mit dem angegebenen Integral führt dies zum Ergebnis:
- $${\rm{MQF}} = \frac{{2{\it \Phi} _0 f_0 }}{{\sqrt {1 + Q} }}\left( {\arctan ( \infty ) - \arctan ( 0 )} \right) = \frac{{{\it \Phi} _0 f_0 {\rm{\pi }}}}{{\sqrt {1 + Q} }}.$$
- Normiert man MQF auf die Nutzleistung $P_s$, so erhält man für $Q=3$:
- $$\frac{\rm{MQF}}{P_s} = \frac{1}{{\sqrt {1 + Q} }} \hspace{0.15cm}\underline { = 0.5}.$$
(4) Aus der Berechnung in in der Teilaufgabe (3) folgt für ${\rm MQF}/P_s \ge 0.1$ direkt die Bedingung $Q \ge 99$ ⇒ $Q_{\rm min} \hspace{0.15cm}\underline{= 99}$.
- Je größer $Q$ ist, desto kleiner wird der mittlere quadratische Fehler.
(5) Richtig ist nur der zweite Lösungsvorschlag:
- Ein zum Wiener–Kolmogorow–Filterr formgleicher Frequenzgang ⇒ $H(f) = K \cdot H_{\rm WF}(f)$ mit $K \ne 1$ führt stets zu großen Verfälschungen.
- Dies kann man sich zum Beispiel am rauschfreien Fall ($Q \to \infty$) verdeutlichen:
- In diesem Fall wäre $d(t) = K \cdot s(t)$ und die Optimierungsaufgabe trotz guter Bedingungen extrem schlecht gelöst.
- Aus der Gleichung
- $${\rm{MQF}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f)} \cdot \it{\Phi} _n (f)\,\,{\rm{d}}f$$
- könnte man fälschlicherweise schließen, dass durch ein Filter $H(f) = 2 \cdot H_{\rm WF}(f))$ der mittlere quadratische Fehler nur verdoppelt wird.
- Dem ist jedoch nicht so, da $H(f)$dann kein Wiener-Filter mehr ist und obige Gleichung auch nicht mehr anwendbar.
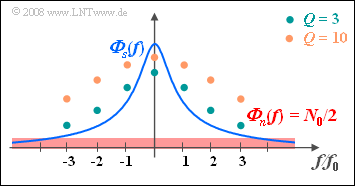
Die zweite Aussage ist zutreffend, wie aus der nebenstehenden Skizze hervorgeht.
- Die Punkte markieren den Frequenzgang $H_{\rm WF}(f))$ des Wiener–Kolmogorow–Filters für $Q = 3$ bzw. für $Q = 10$.
- Bei größerem $Q (= 10)$ werden hohe Anteile weniger gedämpft als bei niedrigerem $Q (= 3)$.
- Deshalb beinhaltet das Filterausgangssignal im Fall $Q = 10$ auch mehr höherfrequente Anteile, die auf das Rauschen $n(t)$ zurückgehen.