Aufgaben:Aufgabe 2.11Z: Nochmals ESB-AM & Hüllkurvendemodulation: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
|||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1050__Mod_Z_2_10.png|right|]] | + | [[Datei:P_ID1050__Mod_Z_2_10.png|right|frame|Äquivalentes Tiefpass–Signal bei ESB-AM]] |
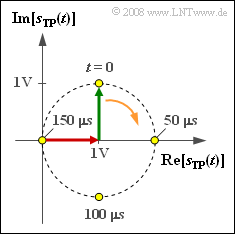
| − | Nebenstehende Grafik zeigt die Ortskurve – also die Darstellung des äquivalenten | + | Nebenstehende Grafik zeigt die Ortskurve – also die Darstellung des äquivalenten Tiefpass–Signals in der komplexen Ebene – für ein ESB–AM–System. |
| − | Weiter ist bekannt, dass die Trägerfrequenz $ | + | Weiter ist bekannt, dass die Trägerfrequenz $f_{\rm T} = 100 \ \rm kHz$ beträgt und dass der Kanal ideal ist: |
| − | $$ r(t) = s(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_{\rm TP}(t) = s_{\rm TP}(t) \hspace{0.05cm}.$$ | + | :$$ r(t) = s(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_{\rm TP}(t) = s_{\rm TP}(t) \hspace{0.05cm}.$$ |
Beim Empfänger wird ein idealer Hüllkurvendemodulator (HKD) eingesetzt. Im Verlauf dieser Aufgabe werden folgende Größen benutzt: | Beim Empfänger wird ein idealer Hüllkurvendemodulator (HKD) eingesetzt. Im Verlauf dieser Aufgabe werden folgende Größen benutzt: | ||
| − | + | *das Seitenband–zu–Träger–Verhältnis | |
| − | $$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.05cm},$$ | + | :$$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.05cm},$$ |
| − | + | *die Hüllkurve | |
| − | $$a(t) = |s_{\rm TP}(t)| \hspace{0.05cm},$$ | + | :$$a(t) = |s_{\rm TP}(t)| \hspace{0.05cm},$$ |
| − | + | * die maximale Abweichung $τ_{\rm max}$ der Nulldurchgänge zwischen Sendesignal $s(t)$ und Trägersignal $z(t)$. | |
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Einseitenbandmodulation|Einseitenbandmodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Einseitenbandmodulation#Seitenband.E2.80.93zu.E2.80.93Tr.C3.A4ger.E2.80.93Verh.C3.A4ltnis|Seitenband-zu-Träger-Verhältnis]]. | ||
| + | *Für diese Aufgabe gelten vergleichbare Voraussetzungen wie für die [[Aufgaben:2.11_Hüllkurvendemodulation_eines_ESB-Signals|Aufgabe 2.11]]. | ||
| + | |||
| − | |||
| Zeile 22: | Zeile 28: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie das äquivalente TP–Signal in analytischer Form an und beantworten Sie folgende Fragen. | + | {Geben Sie das äquivalente TP–Signal $s_{\rm TP}(t)$ in analytischer Form an und beantworten Sie folgende Fragen. |
|type="[]"} | |type="[]"} | ||
- Es handelt sich um eine OSB–AM. | - Es handelt sich um eine OSB–AM. | ||
| Zeile 29: | Zeile 35: | ||
+ Das Nachrichtensignal $q(t)$ ist sinusförmig. | + Das Nachrichtensignal $q(t)$ ist sinusförmig. | ||
| − | {Geben Sie die Amplitude und Frequenz des Quellensignals an. Berücksichtigen Sie, dass es sich um eine ESB–AM handelt. | + | {Geben Sie die Amplitude $A_{\rm N}$ und Frequenz $f_{\rm N}$ des Quellensignals an. Berücksichtigen Sie, dass es sich um eine ESB–AM handelt. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_{\rm N} \ = \ $ { 2 3% } $\ \rm V$ |
| − | $ | + | $f_{\rm N} \ = \ $ { 5 3% } $\ \rm kHz$ |
| − | {Welcher Wert ergibt sich für das | + | {Welcher Wert ergibt sich für das Seitenband–zu–Träger–Verhältnis $μ$? Verwenden Sie diese Größe zur Beschreibung von $s_{\rm TP}(t)$. |
|type="{}"} | |type="{}"} | ||
| − | $μ$ | + | $μ \ = \ $ { 1 3% } |
| − | {Berechnen Sie den zeitlichen Verlauf der Hüllkurve $a(t)$. Welche Werte treten bei $t = 50 μs$, $t = 100 μs$ und $t = 150 μs$ auf? | + | {Berechnen Sie den zeitlichen Verlauf der Hüllkurve $a(t)$. Welche Werte treten bei $t = 50 \ \rm μs$, $t = 100 \ \rm μs$ und $t = 150 \ \rm μs$ auf? |
|type="{}"} | |type="{}"} | ||
| − | $a(t = 50 μs)$ | + | $a(t = 50 \ \rm μs) \hspace{0.32cm} = \ $ { 2 3% } $\ \rm V$ |
| − | $a(t = 100 μs)$ | + | $a(t = 100 \ \rm μs) \ = \ $ { 1.414 3% } $\ \rm V$ |
| − | $a(t = 150 μs)$ | + | $a(t = 150 \ \rm μs) \ = \ $ { 0. } $\ \rm V$ |
| − | {Um welche Zeitdifferenz | + | {Um welche Zeitdifferenz $τ_{\rm max}$ (betragsmäßig) sind die Nulldurchgänge von $s(t)$ gegenüber $z(t)$ maximal verschoben? |
|type="{}"} | |type="{}"} | ||
| − | $τ_{max}$ | + | $τ_{\rm max} \ = \ $ { 2.5 3% } $\ \rm μs$ |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig sind die <u>Lösungsvorschläge 2 und 4</u>: |
| − | $$ s_{\rm TP}(t) = 1\,{\rm V} + {\rm j}\cdot 1\,{\rm V}\cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \hspace{0.05cm}.$$ | + | *Das äquivalente TP–Signal lautet: |
| − | Die Ortskurve ist ein Kreis mit dem Mittelpunkt bei $ | + | :$$ s_{\rm TP}(t) = 1\,{\rm V} + {\rm j}\cdot 1\,{\rm V}\cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \hspace{0.05cm}.$$ |
| − | + | *Die Ortskurve ist ein Kreis mit dem Mittelpunkt bei $A_{\rm T} = 1 \ \rm V$. | |
| + | *Da die Drehung im Uhrzeigersinn erfolgt, handelt es sich um eine USB–AM. | ||
| + | *Der sich drehende (grüne) Zeiger zeigt zum Starzeitpunkt $t = 0$ in Richtung der imaginären Achse. Daraus folgt, dass für das Quellensignal gelten wird: $q(t) = A_{\rm N} \cdot \sin(\omega_{\rm N} \cdot t).$ | ||
| + | |||
| − | '''2 | + | '''(2)''' Bei der USB wird nur das untere Seitenband mit der Zeigerlänge $A_{\rm N}/2 = 1 \ \rm V$ übertragen. Daraus ergibt sich $A_{\rm N}\hspace{0.15cm}\underline { = 2 \ \rm V}$. |
| + | <br>Für eine Umdrehung in der Ortskurve benötigt der Zeiger die Zeit $200 \ \rm μs$. Der Kehrwert hiervon ist die Frequenz $n_{\rm N}\hspace{0.15cm}\underline { = 5 \ \rm kHz}$. | ||
| − | '''3 | + | '''(3)''' Entsprechend der Definition auf der Angabenseite und den Ergebnissen der Teilaufgaben (1) und (2) gilt: |
| − | $$ \mu = \frac{A_{\rm N}/2}{A_{\rm T}}=1\hspace{0.05cm}.$$ | + | :$$ \mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$ |
Damit kann für das äquivalente TP–Signal auch geschrieben werden: | Damit kann für das äquivalente TP–Signal auch geschrieben werden: | ||
| − | $$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + {\rm j} \cdot \mu \cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right),\hspace{0.3cm}{\rm hier}\hspace{0.15cm}\mu | + | :$$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + {\rm j} \cdot \mu \cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right),\hspace{0.3cm}{\rm hier}\hspace{0.15cm}\mu = 1 \hspace{0.05cm}.$$ |
| − | '''4 | + | '''(4)''' Spaltet man die komplexe Exponentialfunktion mit dem Satz von Euler nach Real– und Imaginärteil auf, so erhält man: |
| − | $$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \sin(\omega_{\rm N}\cdot t) + {\rm j} \cos(\omega_{\rm N}\cdot t)\right) \hspace{0.05cm}.$$ | + | :$$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \sin(\omega_{\rm N}\cdot t) + {\rm j} \cos(\omega_{\rm N}\cdot t)\right) \hspace{0.05cm}.$$ |
| − | Durch Anwendung des | + | Durch Anwendung des „Satzes von Pythagoras” kann hierfür auch geschrieben werden: |
| − | $$a(t) = |s_{\rm TP}(t)| = A_{\rm T} \cdot \sqrt{ (1 + \sin(\omega_{\rm N}\cdot t))^2 + \cos^2(\omega_{\rm N}\cdot t)} = | + | :$$a(t) = |s_{\rm TP}(t)| = A_{\rm T} \cdot \sqrt{ (1 + \sin(\omega_{\rm N}\cdot t))^2 + \cos^2(\omega_{\rm N}\cdot t)} = |
| − | + | A_{\rm T} \cdot \sqrt{ 2 + 2 \cdot \sin(2\omega_{\rm N}\cdot t)} \hspace{0.05cm}.$$ | |
| − | Die abgefragten Werte lauten mit $ | + | Die abgefragten Werte lauten mit $A_{\rm T} = 1\ \rm V$: |
| − | $$ a(t = 50\,{\rm \mu s}) \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.3cm}a(t = 100\,{\rm \mu s}) \hspace{0.15cm}\underline {= 1.414\,{\rm V}},\hspace{0.3cm}a(t = 150\,{\rm \mu s}) \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$ | + | :$$ a(t = 50\,{\rm \mu s}) \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.3cm}a(t = 100\,{\rm \mu s}) \hspace{0.15cm}\underline {= 1.414\,{\rm V}},\hspace{0.3cm}a(t = 150\,{\rm \mu s}) \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$ |
Diese Ergebnisse können auch direkt aus der Grafik auf der Angabenseite abgelesen werden. | Diese Ergebnisse können auch direkt aus der Grafik auf der Angabenseite abgelesen werden. | ||
| − | |||
| − | |||
| − | |||
| + | '''(5)''' Ein Hinweis für die Lage der Nulldurchgänge von $s(t)$ gegenüber dem durch das Trägersignal $z(t)$ vorgegebenen Raster liefert die Phasenfunktion $ϕ(t)$. | ||
| + | *Bei der gegebenen Ortskurve können diese Werte zwischen $±π/2\ (±90^\circ)$ annehmen. | ||
| + | *Diese Maximalwerte treten zum Beispiel im Bereich um $t ≈ 150 \ \rm μs$ auf, da hier ein Phasensprung stattfindet. | ||
| + | *Der Zusammenhang zwischen $τ_{\rm max}$ und $\Delta ϕ_{\rm max}$ lautet: | ||
| + | :$$ \tau_{\rm max} = \frac {\Delta \phi_{\rm max}}{2 \pi }\cdot \frac{1 }{f_{\rm T}} = \frac {1}{4}\cdot 10\,{\rm \mu s} \hspace{0.15cm}\underline {= 2.5\,{\rm \mu s}} \hspace{0.05cm}.$$ | ||
| − | + | {{ML-Fuß}} | |
| − | |||
Aktuelle Version vom 18. März 2020, 14:37 Uhr
Nebenstehende Grafik zeigt die Ortskurve – also die Darstellung des äquivalenten Tiefpass–Signals in der komplexen Ebene – für ein ESB–AM–System.
Weiter ist bekannt, dass die Trägerfrequenz $f_{\rm T} = 100 \ \rm kHz$ beträgt und dass der Kanal ideal ist:
- $$ r(t) = s(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_{\rm TP}(t) = s_{\rm TP}(t) \hspace{0.05cm}.$$
Beim Empfänger wird ein idealer Hüllkurvendemodulator (HKD) eingesetzt. Im Verlauf dieser Aufgabe werden folgende Größen benutzt:
- das Seitenband–zu–Träger–Verhältnis
- $$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.05cm},$$
- die Hüllkurve
- $$a(t) = |s_{\rm TP}(t)| \hspace{0.05cm},$$
- die maximale Abweichung $τ_{\rm max}$ der Nulldurchgänge zwischen Sendesignal $s(t)$ und Trägersignal $z(t)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einseitenbandmodulation.
- Bezug genommen wird insbesondere auf die Seite Seitenband-zu-Träger-Verhältnis.
- Für diese Aufgabe gelten vergleichbare Voraussetzungen wie für die Aufgabe 2.11.
Fragebogen
Musterlösung
- Das äquivalente TP–Signal lautet:
- $$ s_{\rm TP}(t) = 1\,{\rm V} + {\rm j}\cdot 1\,{\rm V}\cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \hspace{0.05cm}.$$
- Die Ortskurve ist ein Kreis mit dem Mittelpunkt bei $A_{\rm T} = 1 \ \rm V$.
- Da die Drehung im Uhrzeigersinn erfolgt, handelt es sich um eine USB–AM.
- Der sich drehende (grüne) Zeiger zeigt zum Starzeitpunkt $t = 0$ in Richtung der imaginären Achse. Daraus folgt, dass für das Quellensignal gelten wird: $q(t) = A_{\rm N} \cdot \sin(\omega_{\rm N} \cdot t).$
(2) Bei der USB wird nur das untere Seitenband mit der Zeigerlänge $A_{\rm N}/2 = 1 \ \rm V$ übertragen. Daraus ergibt sich $A_{\rm N}\hspace{0.15cm}\underline { = 2 \ \rm V}$.
Für eine Umdrehung in der Ortskurve benötigt der Zeiger die Zeit $200 \ \rm μs$. Der Kehrwert hiervon ist die Frequenz $n_{\rm N}\hspace{0.15cm}\underline { = 5 \ \rm kHz}$.
(3) Entsprechend der Definition auf der Angabenseite und den Ergebnissen der Teilaufgaben (1) und (2) gilt:
- $$ \mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$
Damit kann für das äquivalente TP–Signal auch geschrieben werden:
- $$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + {\rm j} \cdot \mu \cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right),\hspace{0.3cm}{\rm hier}\hspace{0.15cm}\mu = 1 \hspace{0.05cm}.$$
(4) Spaltet man die komplexe Exponentialfunktion mit dem Satz von Euler nach Real– und Imaginärteil auf, so erhält man:
- $$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \sin(\omega_{\rm N}\cdot t) + {\rm j} \cos(\omega_{\rm N}\cdot t)\right) \hspace{0.05cm}.$$
Durch Anwendung des „Satzes von Pythagoras” kann hierfür auch geschrieben werden:
- $$a(t) = |s_{\rm TP}(t)| = A_{\rm T} \cdot \sqrt{ (1 + \sin(\omega_{\rm N}\cdot t))^2 + \cos^2(\omega_{\rm N}\cdot t)} = A_{\rm T} \cdot \sqrt{ 2 + 2 \cdot \sin(2\omega_{\rm N}\cdot t)} \hspace{0.05cm}.$$
Die abgefragten Werte lauten mit $A_{\rm T} = 1\ \rm V$:
- $$ a(t = 50\,{\rm \mu s}) \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.3cm}a(t = 100\,{\rm \mu s}) \hspace{0.15cm}\underline {= 1.414\,{\rm V}},\hspace{0.3cm}a(t = 150\,{\rm \mu s}) \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$
Diese Ergebnisse können auch direkt aus der Grafik auf der Angabenseite abgelesen werden.
(5) Ein Hinweis für die Lage der Nulldurchgänge von $s(t)$ gegenüber dem durch das Trägersignal $z(t)$ vorgegebenen Raster liefert die Phasenfunktion $ϕ(t)$.
- Bei der gegebenen Ortskurve können diese Werte zwischen $±π/2\ (±90^\circ)$ annehmen.
- Diese Maximalwerte treten zum Beispiel im Bereich um $t ≈ 150 \ \rm μs$ auf, da hier ein Phasensprung stattfindet.
- Der Zusammenhang zwischen $τ_{\rm max}$ und $\Delta ϕ_{\rm max}$ lautet:
- $$ \tau_{\rm max} = \frac {\Delta \phi_{\rm max}}{2 \pi }\cdot \frac{1 }{f_{\rm T}} = \frac {1}{4}\cdot 10\,{\rm \mu s} \hspace{0.15cm}\underline {= 2.5\,{\rm \mu s}} \hspace{0.05cm}.$$