Aufgaben:Aufgabe 3.1: Ortskurve bei Phasenmodulation: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Phasenmodulation (PM) }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |typ…“) |
|||
| (14 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1079__Mod_A_3_1.png|right|frame|Zwei Ortskurven zur Auswahl]] |
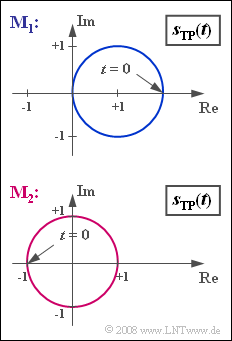
| + | Unter der Ortskurve versteht man allgemein die Darstellung des äquivalenten Tiefpass–Signals $s_{\rm TP}(t)$ in der komplexen Ebene. | ||
| + | *Die Grafik zeigt Ortskurven am Ausgang zweier Modulatoren $\rm M_1$ und $\rm M_2$. | ||
| + | *Real- und Imaginärteil sind in dieser Grafik jeweils auf $1 \ \rm V$ normiert. | ||
| + | |||
| + | |||
| + | Das Quellensignal sei bei beiden Modulatoren gleich: | ||
| + | :$$ q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t),\hspace{1cm} | ||
| + | {\rm mit}\hspace{0.2cm} A_{\rm N} = 2\,{\rm V},\hspace{0.2cm}f_{\rm N} = 5\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| + | Einer der beiden Modulatoren realisiert eine Phasenmodulation, die durch folgende Gleichungen gekennzeichnet ist: | ||
| + | :$$ s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \phi(t) \big]\hspace{0.05cm},$$ | ||
| + | :$$ s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm},$$ | ||
| + | :$$ \phi(t) = K_{\rm PM} \cdot q(t)\hspace{0.05cm}.$$ | ||
| + | Den Maximalwert von $ϕ(t)$ nennt man den ''Modulationsindex'' $η$. Oft wird $η$ in der Literatur auch als ''Phasenhub'' bezeichnet. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Phasenmodulation_(PM)|Phasenmodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Phasenmodulation_(PM)#.C3.84quivalentes_TP.E2.80.93Signal_bei_Phasenmodulation|Äquivalentes TP-Signal bei Phasenmodulation]]. | ||
| + | |||
| Zeile 9: | Zeile 34: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welches Modulationsverfahren verwendet der Modulator $\rm M_1$? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Zweiseitenband–Amplitudenmodulation. |
| − | + | + | + Einseitenband–Amplitudenmodulation. |
| + | - Phasenmodulation. | ||
| + | {Welches Modulationsverfahren verwendet der Modulator $\rm M_2$? | ||
| + | |type="()"} | ||
| + | - Zweiseitenband–Amplitudenmodulation. | ||
| + | - Einseitenband–Amplitudenmodulation. | ||
| + | + Phasenmodulation. | ||
| − | { | + | {Wie groß ist die Trägeramplitude $A_{\rm T}$ beim Phasenmodulator? Beachten Sie die Normierung auf $1 \ \rm V$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $A_{\rm T} \ = \ $ { 1 3% } $\ \rm V$ |
| + | {Welche Werte besitzen der Modulationsindex $η$ und die Modulatorkonstante $K_{\rm PM}$? | ||
| + | |type="{}"} | ||
| + | $η\ = \ $ { 3.1415 3% } | ||
| + | $K_{\rm PM}\ = \ $ { 1.571 3% } $\ \rm 1/V$ | ||
| + | |||
| + | {Beschreiben Sie die Bewegung auf der Ortskurve. Zu welcher Zeit $t_1$ wird erstmals wieder der Ausgangspunkt $s_{\rm TP}(t = 0) = -1 \ \rm V$ erreicht? | ||
| + | |type="{}"} | ||
| + | $t_1\ = \ $ { 100 3% } $ \ \rm µ s$ | ||
| Zeile 25: | Zeile 64: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Es handelt sich um eine ESB–AM mit dem Seitenband–zu–Träger–Verhältnis $μ = 1$ ⇒ <u>Antwort 2</u>: |
| − | '''2 | + | *Bewegt man sich auf dem Kreis in mathematisch positive Richtung, so liegt speziell eine OSB–AM vor, andernfalls eine USB–AM. |
| − | '''3 | + | *Die Phasenfunktion $ϕ(t)$ als der Winkel eines Punktes $s_{\rm TP}(t)$ auf dem Kreis(bogen) bezogen auf den Koordinatenursprung kann Werte zwischen $±π/2$ annehmen und zeigt keinen Cosinusverlauf. |
| − | '''4 | + | *Aber auch die Hüllkurve $a(t) = |s_{\rm TP}(t)|$ ist nicht cosinusförmig. |
| − | '''5 | + | *Würde man beim Empfänger für $\rm M_1$ einen Hüllkurvendemodulator einsetzen, so käme es zu nichtlinearen Verzerrungen im Gegensatz zur ZSB–AM, deren Ortskurve eine horizontale Gerade ist. |
| − | + | ||
| − | + | ||
| + | |||
| + | |||
| + | '''(2)''' Hier handelt es sich um die Phasenmodulation ⇒ <u>Antwort 3</u>: | ||
| + | *Die Einhüllende $a(t) = A_{\rm T}$ ist konstant, | ||
| + | *während die Phase $ϕ(t)$ entsprechend dem Quellensignal $q(t)$ cosinusförmig verläuft. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Bei der Phasenmodulation gilt: | ||
| + | :$$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm}.$$ | ||
| + | *Aus der Grafik kann man die Trägeramplitude $A_{\rm T}\hspace{0.15cm}\underline{ = 1 \ \rm V}$ als den Kreisradius ablesen. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Das Quellensignal $q(t)$ ist zum Zeitpunkt $t = 0$ maximal und damit auch die Phasenfunktion: | ||
| + | :$$ \eta = \phi_{\rm max} = \phi( t =0) = \pi\hspace{0.15cm}\underline { = 3.1415} \hspace{0.05cm}.$$ | ||
| + | *Daraus erhält man für die Modulatorkonstante: | ||
| + | $$K_{\rm PM} = \frac{\eta}{A_{\rm N}} = \frac{\pi}{2\,{\rm V}}\hspace{0.15cm}\underline {= 1.571\,{\rm V}^{-1}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Man bewegt sich auf dem Kreis(bogen) im Uhrzeigersinn. | ||
| + | *Nach einem Viertel der Periodendauer $T_{\rm N} = 1/f_{\rm N} = 200 \ \rm µ s$ ist $ϕ(t) = 0$ und $s_{\rm TP}(t) = 1 \, \rm V$. | ||
| + | *Zur Zeit $t_1 = T_{\rm N}/2\hspace{0.15cm}\underline { = 100 \ \rm µ s}$ gilt $ϕ(t_1) = -π$ und $s_{\rm TP}(t_1) = -1 \, \rm V$. | ||
| + | *Danach bewegt man sich auf dem Kreisbogen entgegen dem Uhrzeigersinn. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 24. März 2020, 16:48 Uhr
Unter der Ortskurve versteht man allgemein die Darstellung des äquivalenten Tiefpass–Signals $s_{\rm TP}(t)$ in der komplexen Ebene.
- Die Grafik zeigt Ortskurven am Ausgang zweier Modulatoren $\rm M_1$ und $\rm M_2$.
- Real- und Imaginärteil sind in dieser Grafik jeweils auf $1 \ \rm V$ normiert.
Das Quellensignal sei bei beiden Modulatoren gleich:
- $$ q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t),\hspace{1cm} {\rm mit}\hspace{0.2cm} A_{\rm N} = 2\,{\rm V},\hspace{0.2cm}f_{\rm N} = 5\,{\rm kHz}\hspace{0.05cm}.$$
Einer der beiden Modulatoren realisiert eine Phasenmodulation, die durch folgende Gleichungen gekennzeichnet ist:
- $$ s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \phi(t) \big]\hspace{0.05cm},$$
- $$ s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm},$$
- $$ \phi(t) = K_{\rm PM} \cdot q(t)\hspace{0.05cm}.$$
Den Maximalwert von $ϕ(t)$ nennt man den Modulationsindex $η$. Oft wird $η$ in der Literatur auch als Phasenhub bezeichnet.
Hinweise:
- Die Aufgabe gehört zum Kapitel Phasenmodulation.
- Bezug genommen wird insbesondere auf die Seite Äquivalentes TP-Signal bei Phasenmodulation.
Fragebogen
Musterlösung
- Bewegt man sich auf dem Kreis in mathematisch positive Richtung, so liegt speziell eine OSB–AM vor, andernfalls eine USB–AM.
- Die Phasenfunktion $ϕ(t)$ als der Winkel eines Punktes $s_{\rm TP}(t)$ auf dem Kreis(bogen) bezogen auf den Koordinatenursprung kann Werte zwischen $±π/2$ annehmen und zeigt keinen Cosinusverlauf.
- Aber auch die Hüllkurve $a(t) = |s_{\rm TP}(t)|$ ist nicht cosinusförmig.
- Würde man beim Empfänger für $\rm M_1$ einen Hüllkurvendemodulator einsetzen, so käme es zu nichtlinearen Verzerrungen im Gegensatz zur ZSB–AM, deren Ortskurve eine horizontale Gerade ist.
(2) Hier handelt es sich um die Phasenmodulation ⇒ Antwort 3:
- Die Einhüllende $a(t) = A_{\rm T}$ ist konstant,
- während die Phase $ϕ(t)$ entsprechend dem Quellensignal $q(t)$ cosinusförmig verläuft.
(3) Bei der Phasenmodulation gilt:
- $$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm}.$$
- Aus der Grafik kann man die Trägeramplitude $A_{\rm T}\hspace{0.15cm}\underline{ = 1 \ \rm V}$ als den Kreisradius ablesen.
(4) Das Quellensignal $q(t)$ ist zum Zeitpunkt $t = 0$ maximal und damit auch die Phasenfunktion:
- $$ \eta = \phi_{\rm max} = \phi( t =0) = \pi\hspace{0.15cm}\underline { = 3.1415} \hspace{0.05cm}.$$
- Daraus erhält man für die Modulatorkonstante:
$$K_{\rm PM} = \frac{\eta}{A_{\rm N}} = \frac{\pi}{2\,{\rm V}}\hspace{0.15cm}\underline {= 1.571\,{\rm V}^{-1}}\hspace{0.05cm}.$$
(5) Man bewegt sich auf dem Kreis(bogen) im Uhrzeigersinn.
- Nach einem Viertel der Periodendauer $T_{\rm N} = 1/f_{\rm N} = 200 \ \rm µ s$ ist $ϕ(t) = 0$ und $s_{\rm TP}(t) = 1 \, \rm V$.
- Zur Zeit $t_1 = T_{\rm N}/2\hspace{0.15cm}\underline { = 100 \ \rm µ s}$ gilt $ϕ(t_1) = -π$ und $s_{\rm TP}(t_1) = -1 \, \rm V$.
- Danach bewegt man sich auf dem Kreisbogen entgegen dem Uhrzeigersinn.