Aufgaben:Exercise 1.1: Dual Slope Loss Model: Unterschied zwischen den Versionen
Javier (Diskussion | Beiträge) K (Javier verschob die Seite Exercises:Exercise 1.1: Dual Slope Loss Model nach Exercise 1.1: Dual Slope Loss Model) |
Javier (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID2120__Mob_A_1_1.png|right|frame|Dual-Slope-Pfadverlustmodell]] | [[Datei:P_ID2120__Mob_A_1_1.png|right|frame|Dual-Slope-Pfadverlustmodell]] | ||
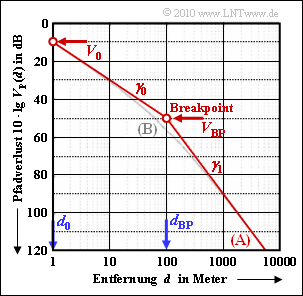
| − | + | To simulate path loss in an urban environment, the asymptotic dual-slope model is often used, which is shown as a red curve in the diagram. This simple model is characterized by two linear sections separated by the so-called breakpoint (BP): | |
| − | * | + | * For $d \le d_{\rm BP}$ and the exponent is $\gamma_0$ we have: |
| − | + | $$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_0})\hspace{0.05cm}.$$ | |
| − | * | + | * For $d > d_{\rm BP}$ we must apply the path loss exponent $\gamma_1$ where $\gamma_1 > \gamma_0$ applies: |
| − | + | $$V_{\rm P}(d) = V_{\rm BP} + \gamma_1 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_{\rm BP}})\hspace{0.05cm}.$$ | |
| − | In | + | In these equations, the variables are: |
| − | * $V_0$ | + | * $V_0$ is the path loss (in dB) at $d_0$ (normalization distance). |
| − | * $V_{\rm BP}$ | + | * $V_{\rm BP}$ is the path loss (in dB) at $d=d_{\rm BP}$ ("Breakpoint"). |
| − | + | The graph applies to the model parameters | |
| − | + | $$d_0 = 1\,{\rm m}\hspace{0.05cm},\hspace{0.2cm}d_{\rm BP} = 100\,{\rm m}\hspace{0.05cm},\hspace{0.2cm} | |
V_0 = 10\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm}\gamma_0 = 2 \hspace{0.05cm},\hspace{0.2cm}\gamma_1 = 4 \hspace{0.3cm} | V_0 = 10\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm}\gamma_0 = 2 \hspace{0.05cm},\hspace{0.2cm}\gamma_1 = 4 \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} | \Rightarrow \hspace{0.3cm} | ||
V_{\rm BP} = 50\,{\rm dB}\hspace{0.05cm}.$$ | V_{\rm BP} = 50\,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | In | + | In the questions, this piece-wise defined profile is called $\rm A$. |
| − | + | The second curve is the profile $\rm B$ given by the following equation: | |
| − | + | $$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ( {d}/{d_0} \right ) | |
+ (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )\hspace{0.05cm}.$$ | + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )\hspace{0.05cm}.$$ | ||
| − | + | With this dual model, the entire distance course can be written in closed form, and the received power depends on the distance $d$ according to the following equation: | |
| − | + | $$P_{\rm E}(d) = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} /V_{\rm zus}}}{K_{\rm P}(d)} | |
\hspace{0.05cm},\hspace{0.2cm}K_{\rm P}(d) = 10^{V_{\rm P}(d)/10} | \hspace{0.05cm},\hspace{0.2cm}K_{\rm P}(d) = 10^{V_{\rm P}(d)/10} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Here, all parameters are in natural units (not in dB). The transmit power is assumed to be $P_{\rm S} = 5 \ \rm W$ . The other quantities have the following meanings and values: | |
| − | * $10 \cdot \lg \ G_{\rm S} = 17 \ \rm dB$ ( | + | * $10 \cdot \lg \ G_{\rm S} = 17 \ \rm dB$ (gain of the transmit antenna), |
| − | * $10 \cdot \lg \ G_{\rm E} = -3 \ \rm dB$ ( | + | * $10 \cdot \lg \ G_{\rm E} = -3 \ \ \rm dB$ (gain of receiving antenna – so actually a loss), |
| − | * $10 \cdot \lg \ V_{\rm zus} = 4 \ \rm dB$ ( | + | * $10 \cdot \lg \ V_{\rm zus} = 4 \ \ \rm dB$ (loss through feeds). |
| Zeile 42: | Zeile 42: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The task belongs to the chapter [[Mobile_Communication/Distancedependent%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Distance-dependent attenuation and shading]]. |
| − | * | + | *If the profile were profile $\rm B$ corresponding to |
| − | + | $$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} \left ( {d}/{d_0} \right ) | |
+ (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right )$$ | + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right )$$ | ||
| − | : | + | :define, then profile $\rm A$ and profile $\rm B$ for $d ≥ d_{\rm BP}$ would be identical |
| − | *In | + | *In this case, however, the lower area would contain $(d < d_{\rm BP})$ the profile $\rm B$ would be above profile $\rm A$ , thus suggesting clearly too good conditions. For example, $d = d_0 = 1 \ \ \rm m$ with the given numerical values gives a result that is $40 \ \ \rm dB$ too good: |
| − | + | $$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right ) =10\,{\rm dB} + 2 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({1}/{100} \right ) | |
= -30\,{\rm dB} \hspace{0.05cm}. $$ | = -30\,{\rm dB} \hspace{0.05cm}. $$ | ||
| Zeile 55: | Zeile 55: | ||
| − | === | + | ===Questionnaire== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How large is the path loss $($in $\rm dB)$ to $d= 100 \ \rm m$ according to profile $\rm A$? |
|type="{}"} | |type="{}"} | ||
$V_{\rm P}(d = 100 \ \rm m) \ = \ $ { 50 3% } $\ \rm dB$ | $V_{\rm P}(d = 100 \ \rm m) \ = \ $ { 50 3% } $\ \rm dB$ | ||
| − | { | + | {How large is the path loss $($in $\rm dB)$ to $d= 100 \ \rm m$ according to profile $\rm B$? |
|type="{}"} | |type="{}"} | ||
$V_{\rm P}(d = 100 \ \rm m) \ = \ $ { 56 3% } $\ \rm dB$ | $V_{\rm P}(d = 100 \ \rm m) \ = \ $ { 56 3% } $\ \rm dB$ | ||
| − | { | + | {What is the receive power after $100 \ \ \rm m$ with both profiles? |
| − | |type="{}"} | + | |type="{}"{} |
| − | + | Profile $\text{A:} \hspace{0.2cm} P_{\rm E}(d = 100 \ \rm m) \ = \ $ { 0.5 3% } $\ \ \rm mW$ | |
| − | + | Profile $\text{B:} \hspace{0.2cm} P_{\rm E}(d = 100 \ \rm m) \ = \ $ { 0.125 3% } $\ \ \rm mW$ | |
| − | { | + | {How big is the deviation $ΔV_{\rm P}$ between profile $\rm A$ and $\rm B$ at $d = 50 \ \rm m$? |
|type="{}"} | |type="{}"} | ||
$ΔV_{\rm P}(d = 50 \ \rm m) \ = \ $ { 3.5 3% } $\ \rm dB$ | $ΔV_{\rm P}(d = 50 \ \rm m) \ = \ $ { 3.5 3% } $\ \rm dB$ | ||
| − | { | + | {How big is the deviation $ΔV_{\rm P}$ between profile $\rm A$ and $\rm B$ at $d = 200 \ \rm m$? |
|type="{}"} | |type="{}"} | ||
$ΔV_{\rm P}(d = 200 \ \rm m)\ = \ $ { 3.5 3% } $\ \rm dB$ | $ΔV_{\rm P}(d = 200 \ \rm m)\ = \ $ { 3.5 3% } $\ \rm dB$ | ||
| − | </quiz | + | </quiz |
| − | === | + | === sample solution=== |
| − | {{ML | + | {{ML head}} |
| − | '''(1)''' | + | '''(1)''' You can see directly from the graphic that the profile '''(A)'' with the two linear sections at „Breakpoint” $(d = 100 \ \rm m)$ gives the following result: |
| − | + | $$V_{\rm P}(d = 100\,{\rm m})\hspace{0.15cm} \underline{= 50\,{\rm dB}} \hspace{0.05cm}.$$ | |
| − | '''(2)''' | + | '''(2)''' With the profile <b>(B)</b> on the other hand, using $V_0 = 10 \ \rm dB$, $\gamma_0 = 2$ and $\gamma_1 = 4$: |
| − | + | $$V_{\rm P}(d = 100\,{\rm m}) = 10\,{\rm dB} + 20\,{\rm dB}\cdot {\rm lg} \hspace{0.1cm}(100)+ 20\,{\rm dB}\cdot {\rm lg} \hspace{0.1cm}(2) | |
\hspace{0.15cm} \underline{\approx 56\,{\rm dB}} \hspace{0.05cm}.$$ | \hspace{0.15cm} \underline{\approx 56\,{\rm dB}} \hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The antenna gains from the transmitter $(+17 \ \ \rm dB)$ and receiver $(-3 \ \rm dB)$ and the internal losses of the base station $(+4 \ \rm dB)$ can be combined to |
| − | + | $$10 \cdot {\rm lg}\hspace{0.1cm} G = 10 \cdot {\rm lg}\hspace{0.1cm} G_{\rm S} + 10 \cdot {\rm lg} \hspace{0.1cm} G_{\rm E} - 10 \cdot {\rm lg}\hspace{0.1cm} V_{\rm zus} = 17\,{\rm dB} -3\,{\rm dB} - 4\,{\rm dB} = 10\,{\rm dB} | |
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {G = 10} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {G = 10} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *For the profile '''(A)'' the following path loss occurred: |
| − | + | $$V_{\rm P}(d = 100\,{\rm m})\hspace{0.05cm} {= 50\,{\rm dB}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K_{\rm P} = 10^5 \hspace{0.05cm}.$$ | |
| − | : | + | :This gives you \ \ \rm m$ for the receiving power after $d = 100: |
| − | + | $$P_{\rm E}(d = 100\,{\rm m}) = \frac{P_{\rm S} \cdot G}{K_{\rm P}} = \frac{5\,{\,} \cdot 10}{10^5}\hspace{0.15cm} \underline{= 0.5\,{\rm mW}} \hspace{0.05cm}.$$ | |
| − | * | + | *For profile '''(B)'' the receiving power is about $4$ less: |
:$$P_{\rm E}(d = 100\,{\rm m}) = \frac{5\,{\rm W} \cdot 10}{10^{5.6}}\approx \frac{5\,{\rm W} \cdot 10}{4 \cdot 10^{5}}\hspace{0.15cm} \underline{= 0.125\,{\rm mW}} \hspace{0.05cm}.$$ | :$$P_{\rm E}(d = 100\,{\rm m}) = \frac{5\,{\rm W} \cdot 10}{10^{5.6}}\approx \frac{5\,{\rm W} \cdot 10}{4 \cdot 10^{5}}\hspace{0.15cm} \underline{= 0.125\,{\rm mW}} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' Below the breakpoint $(d < 100 \ \rm m)$ the deviation is determined by the last summand of profile '''(B)''': |
| − | + | $${\rm \delta}V_{\rm P}(d = 50\,{\rm m}) = (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )= (4-2) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (1.5)\hspace{0.15cm} | |
\underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$ | \underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' Here the profile '''(A)'' with $V_{\rm BP} = 50 \ \rm dB$: |
| − | + | $$V_{\rm P}(d = 200\,{\rm m}) = 50\,{\rm dB} + 4 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (2)\hspace{0.15cm} | |
{\approx 62\,{\rm dB}} \hspace{0.05cm}.$$ | {\approx 62\,{\rm dB}} \hspace{0.05cm}.$$ | ||
| − | * | + | *On the other hand, the profile '''(B)'' leads to the result: |
| − | + | $$V_{\rm P}(d = 200\,{\rm m}) = 50\,{\rm dB} + 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (200) | |
+ 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (3) = 10\,{\rm dB} + 46\,{\rm dB} + 9.5\,{\rm dB} | + 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (3) = 10\,{\rm dB} + 46\,{\rm dB} + 9.5\,{\rm dB} | ||
\hspace{0.15cm} {\approx 65.5\,{\rm dB}}$$ | \hspace{0.15cm} {\approx 65.5\,{\rm dB}}$$ | ||
| − | + | $$\Rightarrow \hspace{0.3cm} {\rm \delta}V_{\rm P}(d = 200\,{\rm m}) = 65.5\,{\rm dB} - 62\,{\rm dB}\hspace{0.15cm} | |
\underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$ | \underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$ | ||
| − | * | + | *You can see that $\Delta V_{\rm P}$ is almost symmetrical to $d = d_{\rm BP}$ if you plot the distance $d$ logarithmically as in the given graph. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 25. März 2020, 14:57 Uhr
To simulate path loss in an urban environment, the asymptotic dual-slope model is often used, which is shown as a red curve in the diagram. This simple model is characterized by two linear sections separated by the so-called breakpoint (BP):
- For $d \le d_{\rm BP}$ and the exponent is $\gamma_0$ we have:
$$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_0})\hspace{0.05cm}.$$
- For $d > d_{\rm BP}$ we must apply the path loss exponent $\gamma_1$ where $\gamma_1 > \gamma_0$ applies:
$$V_{\rm P}(d) = V_{\rm BP} + \gamma_1 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_{\rm BP}})\hspace{0.05cm}.$$
In these equations, the variables are:
- $V_0$ is the path loss (in dB) at $d_0$ (normalization distance).
- $V_{\rm BP}$ is the path loss (in dB) at $d=d_{\rm BP}$ ("Breakpoint").
The graph applies to the model parameters
$$d_0 = 1\,{\rm m}\hspace{0.05cm},\hspace{0.2cm}d_{\rm BP} = 100\,{\rm m}\hspace{0.05cm},\hspace{0.2cm}
V_0 = 10\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm}\gamma_0 = 2 \hspace{0.05cm},\hspace{0.2cm}\gamma_1 = 4 \hspace{0.3cm}
\Rightarrow \hspace{0.3cm}
V_{\rm BP} = 50\,{\rm dB}\hspace{0.05cm}.$$
In the questions, this piece-wise defined profile is called $\rm A$.
The second curve is the profile $\rm B$ given by the following equation: $$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )\hspace{0.05cm}.$$
With this dual model, the entire distance course can be written in closed form, and the received power depends on the distance $d$ according to the following equation: $$P_{\rm E}(d) = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} /V_{\rm zus}}}{K_{\rm P}(d)} \hspace{0.05cm},\hspace{0.2cm}K_{\rm P}(d) = 10^{V_{\rm P}(d)/10} \hspace{0.05cm}.$$
Here, all parameters are in natural units (not in dB). The transmit power is assumed to be $P_{\rm S} = 5 \ \rm W$ . The other quantities have the following meanings and values:
- $10 \cdot \lg \ G_{\rm S} = 17 \ \rm dB$ (gain of the transmit antenna),
- $10 \cdot \lg \ G_{\rm E} = -3 \ \ \rm dB$ (gain of receiving antenna – so actually a loss),
- $10 \cdot \lg \ V_{\rm zus} = 4 \ \ \rm dB$ (loss through feeds).
Notes:
- The task belongs to the chapter Distance-dependent attenuation and shading.
- If the profile were profile $\rm B$ corresponding to
$$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right )$$
- define, then profile $\rm A$ and profile $\rm B$ for $d ≥ d_{\rm BP}$ would be identical
- In this case, however, the lower area would contain $(d < d_{\rm BP})$ the profile $\rm B$ would be above profile $\rm A$ , thus suggesting clearly too good conditions. For example, $d = d_0 = 1 \ \ \rm m$ with the given numerical values gives a result that is $40 \ \ \rm dB$ too good:
$$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right ) =10\,{\rm dB} + 2 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({1}/{100} \right ) = -30\,{\rm dB} \hspace{0.05cm}. $$
=Questionnaire
<quiz display=simple> {How large is the path loss $($in $\rm dB)$ to $d= 100 \ \rm m$ according to profile $\rm A$? |type="{}"} $V_{\rm P}(d = 100 \ \rm m) \ = \ $ { 50 3% } $\ \rm dB$
{How large is the path loss $($in $\rm dB)$ to $d= 100 \ \rm m$ according to profile $\rm B$? |type="{}"} $V_{\rm P}(d = 100 \ \rm m) \ = \ $ { 56 3% } $\ \rm dB$
{What is the receive power after $100 \ \ \rm m$ with both profiles? |type="{}"{} Profile $\text{A:} \hspace{0.2cm} P_{\rm E}(d = 100 \ \rm m) \ = \ $ { 0.5 3% } $\ \ \rm mW$ Profile $\text{B:} \hspace{0.2cm} P_{\rm E}(d = 100 \ \rm m) \ = \ $ { 0.125 3% } $\ \ \rm mW$
{How big is the deviation $ΔV_{\rm P}$ between profile $\rm A$ and $\rm B$ at $d = 50 \ \rm m$? |type="{}"} $ΔV_{\rm P}(d = 50 \ \rm m) \ = \ $ { 3.5 3% } $\ \rm dB$
{How big is the deviation $ΔV_{\rm P}$ between profile $\rm A$ and $\rm B$ at $d = 200 \ \rm m$? |type="{}"} $ΔV_{\rm P}(d = 200 \ \rm m)\ = \ $ { 3.5 3% } $\ \rm dB$ </quiz
sample solution
ML head '(1) You can see directly from the graphic that the profile (A) with the two linear sections at „Breakpoint” $(d = 100 \ \rm m)$ gives the following result: $$V_{\rm P}(d = 100\,{\rm m})\hspace{0.15cm} \underline{= 50\,{\rm dB}} \hspace{0.05cm}.$$
(2) With the profile (B) on the other hand, using $V_0 = 10 \ \rm dB$, $\gamma_0 = 2$ and $\gamma_1 = 4$: $$V_{\rm P}(d = 100\,{\rm m}) = 10\,{\rm dB} + 20\,{\rm dB}\cdot {\rm lg} \hspace{0.1cm}(100)+ 20\,{\rm dB}\cdot {\rm lg} \hspace{0.1cm}(2) \hspace{0.15cm} \underline{\approx 56\,{\rm dB}} \hspace{0.05cm}.$$
(3) The antenna gains from the transmitter $(+17 \ \ \rm dB)$ and receiver $(-3 \ \rm dB)$ and the internal losses of the base station $(+4 \ \rm dB)$ can be combined to $$10 \cdot {\rm lg}\hspace{0.1cm} G = 10 \cdot {\rm lg}\hspace{0.1cm} G_{\rm S} + 10 \cdot {\rm lg} \hspace{0.1cm} G_{\rm E} - 10 \cdot {\rm lg}\hspace{0.1cm} V_{\rm zus} = 17\,{\rm dB} -3\,{\rm dB} - 4\,{\rm dB} = 10\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {G = 10} \hspace{0.05cm}.$$
- For the profile '(A) the following path loss occurred:
$$V_{\rm P}(d = 100\,{\rm m})\hspace{0.05cm} {= 50\,{\rm dB}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K_{\rm P} = 10^5 \hspace{0.05cm}.$$
- This gives you \ \ \rm m$ for the receiving power after $d = 100:
$$P_{\rm E}(d = 100\,{\rm m}) = \frac{P_{\rm S} \cdot G}{K_{\rm P}} = \frac{5\,{\,} \cdot 10}{10^5}\hspace{0.15cm} \underline{= 0.5\,{\rm mW}} \hspace{0.05cm}.$$
- For profile '(B) the receiving power is about $4$ less:
- $$P_{\rm E}(d = 100\,{\rm m}) = \frac{5\,{\rm W} \cdot 10}{10^{5.6}}\approx \frac{5\,{\rm W} \cdot 10}{4 \cdot 10^{5}}\hspace{0.15cm} \underline{= 0.125\,{\rm mW}} \hspace{0.05cm}.$$
(4) Below the breakpoint $(d < 100 \ \rm m)$ the deviation is determined by the last summand of profile (B): $${\rm \delta}V_{\rm P}(d = 50\,{\rm m}) = (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )= (4-2) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (1.5)\hspace{0.15cm} \underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$
'(5) Here the profile (A) with $V_{\rm BP} = 50 \ \rm dB$: $$V_{\rm P}(d = 200\,{\rm m}) = 50\,{\rm dB} + 4 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (2)\hspace{0.15cm} {\approx 62\,{\rm dB}} \hspace{0.05cm}.$$
- On the other hand, the profile '(B) leads to the result:
$$V_{\rm P}(d = 200\,{\rm m}) = 50\,{\rm dB} + 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (200) + 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (3) = 10\,{\rm dB} + 46\,{\rm dB} + 9.5\,{\rm dB} \hspace{0.15cm} {\approx 65.5\,{\rm dB}}$$ $$\Rightarrow \hspace{0.3cm} {\rm \delta}V_{\rm P}(d = 200\,{\rm m}) = 65.5\,{\rm dB} - 62\,{\rm dB}\hspace{0.15cm} \underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$
- You can see that $\Delta V_{\rm P}$ is almost symmetrical to $d = d_{\rm BP}$ if you plot the distance $d$ logarithmically as in the given graph.