Aufgaben:Aufgabe 5.3Z: Realisierung einer PN–Sequenz: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
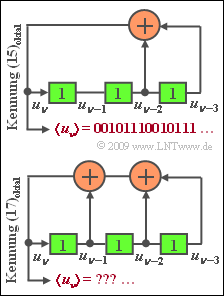
| − | [[Datei:P_ID1886__Mod_Z_5_3.png|right|frame| | + | [[Datei:P_ID1886__Mod_Z_5_3.png|right|frame|Zwei mögliche Realisierungen für PN–Generatoren]] |
Die Grafik zeigt zwei mögliche Generatoren zur Erzeugung von PN–Sequenzen in unipolarer Darstellung: $u_ν ∈ \{0, 1\}$. | Die Grafik zeigt zwei mögliche Generatoren zur Erzeugung von PN–Sequenzen in unipolarer Darstellung: $u_ν ∈ \{0, 1\}$. | ||
*Der obere Generator mit den Koeffizienten | *Der obere Generator mit den Koeffizienten | ||
| Zeile 14: | Zeile 14: | ||
:$$P = 2^G – 1.$$ | :$$P = 2^G – 1.$$ | ||
:Hierbei bezeichnet $G$ den Grad des Schieberegisters, der gleich der Anzahl der Speicherzellen ist. | :Hierbei bezeichnet $G$ den Grad des Schieberegisters, der gleich der Anzahl der Speicherzellen ist. | ||
| + | |||
| + | |||
| + | |||
| Zeile 43: | Zeile 46: | ||
+ In jeder Periode gibt es eine Eins mehr als Nullen. | + In jeder Periode gibt es eine Eins mehr als Nullen. | ||
+ Die maximale Anzahl aufeinander folgender Einsen ist $G$. | + Die maximale Anzahl aufeinander folgender Einsen ist $G$. | ||
| − | + Die Folge & | + | + Die Folge $1 0 1 0 1 0$ ... ist nicht möglich. |
{Geben Sie die Periodenlänge $P$ des PN–Generators mit der Oktalkennung $(17)$ an. | {Geben Sie die Periodenlänge $P$ des PN–Generators mit der Oktalkennung $(17)$ an. | ||
Version vom 30. April 2020, 16:22 Uhr
Die Grafik zeigt zwei mögliche Generatoren zur Erzeugung von PN–Sequenzen in unipolarer Darstellung: $u_ν ∈ \{0, 1\}$.
- Der obere Generator mit den Koeffizienten
- $$ g_0 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_1 = 0 \hspace{0.05cm}, \hspace{0.2cm}g_2 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_3 = 1 \hspace{0.05cm}$$
- wird durch die Oktalkennung $(g_3, g_2, g_1, g_0)_{\rm oktal} = (15)$ bezeichnet.
- Entsprechend ist die Oktalkennung des zweiten PN–Generators gleich $(17)$.
- Man spricht von einer M–Sequenz, wenn für die Periodenlänge der Folge $〈u_ν〉$ gilt:
- $$P = 2^G – 1.$$
- Hierbei bezeichnet $G$ den Grad des Schieberegisters, der gleich der Anzahl der Speicherzellen ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Spreizfolgen für CDMA.
- Bezug genommen wird aber auch auf das Kapitel Erzeugung von diskreten Zufallsgrößen im Buch „Stochastische Signaltheorie”.
- Wir möchten Sie gerne auch auf das Lernvideo Erläuterung der PN–Generatoren an einem Beispiel hinweisen.
Fragebogen
Musterlösung
(1) Der Grad $\underline{G = 3}$ ist gleich der Anzahl der Speicherzellen des Schieberegisters.
(2) Aus der angegebenen Folge ist die Periodenlänge $\underline{P = 7}$ ablesbar. Wegen $P = 2^G –1$ handelt es sich um eine M–Sequenz.
(3) Richtig sind die Lösungsvorschläge 2, 3 und 4:
- Die maximale Anzahl aufeinander folgender Einsen ist $G$ (nämlich immer dann, wenn in allen $G$ Speicherzellen eine Eins steht).
- Es ist dagegen nicht möglich, dass alle Speicherzellen mit Nullen belegt sind (da sonst nur noch Nullen erzeugt würden).
- Deshalb gibt es stets eine Eins mehr als Nullen.
- Die Periodenlänge der letzten Folge beträgt $P = 2$. Bei einer M–Sequenz gilt $P = 2^G –1$. Für keinen Wert von $G$ ist $P = 2$ möglich.
(4) Sind alle Speicherzellen mit Einsen belegt, so liefert der Generator mit der Oktalkennung (17) wieder eine $1$:
- $$u_{\nu} \big [ u_{\nu-1} + u_{\nu-2} + u_{\nu-3} \big ] \,\,{\rm mod} \,\,2 =1 \hspace{0.05cm}.$$
Da sich so an der Speicherbelegung nichts ändert, werden auch alle weiteren erzeugten Binärwerte jeweils $1$ sein ⇒ $\underline{P = 1}$.
(5) Richtig ist die Antwort 1:
- Von einer M–Sequenz spricht man nur dann, wenn $P = 2^G –1$ gilt.
- „M” steht hierbei für „Maximal”.