Aufgaben:Aufgabe 2.1: Gleichrichtung

• Zurück zum Buch

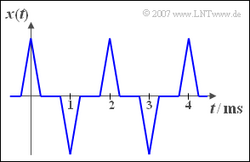
Die Grafik zeigt das periodische Signal $x(t)$. Legt man $x(t)$ an den Eingang einer Nichtlinearität mit der Kennlinie

$$y=g(x)=\left\{ {x \; \rm f\ddot{u}r\; \it x \geq \rm 0, \atop {\rm 0 \;\;\; \rm sonst,}}\right.$$

so erhält man am Ausgang das Signal $y(t)$. Eine zweite nichtlineare Kennlinie

$$z=h(x)=|x|$$

liefert das Signal $z(t)$.

Fragebogen zu "Aufgaben:2.1 Gleichrichtung"

1

Welche der nachfolgenden Aussagen sind zutreffend?

	$y = g(x)$ beschreibt einen Einweggleichrichter.
	$y = g(x)$ beschreibt einen Zweiweggleichrichter.
	$z = h(x)$ beschreibt einen Einweggleichrichter.
	$z = h(x)$ beschreibt einen Zweiweggleichrichter

2

Wie groß ist die Grundfrequenz $f_0$ des Signals $x(t)$?

$f_0$ = Hz

3

Wie groß ist die Periodendauer des Signals $y(t)$?

$T_0$ = ms

4

Wie groß ist die Grundkreisfrequenz des Signals $z(t)$?

$\omega_0$ = 1/s

Musterlösung zu "A1.1 Musiksignale"

Musterlösung

1. Die nichtlineare Kennlinie $y = g(x)$ beschreibt einen Einweggleichrichter und $z = h(x) = |x|$ einen Zweiweggleichrichter ⇒ Richtig sind die Lösungsvorschläge 1 und 4.

2. Die Periodendauer des gegebenen Signals $x(t)$ beträgt $T_0 = 2$ ms. Der Kehrwert hiervon ergibt die Grundfrequenz $f_0 = 500$ Hz.

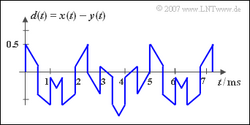
3. Wie aus der folgenden linken Skizze hervorgeht, ändert sich durch die Einweggleichrichtung nichts an der Periodendauer. Das heißt: $T_0$ ist weiterhin 2 ms.

4. Das Signal z(t) nach der Doppelweggleichrichtung hat dagegen die doppelte Frequenz (siehe rechtes Bild). Es gelten dann folgende Werte: $T_0 = 1$ ms, $f_0 = 1$ kHz und $\omega_0 = 6283$ 1/s.