Aufgaben:Exercise 1.3: Rayleigh Fading: Unterschied zwischen den Versionen
Javier (Diskussion | Beiträge) |
|||
| (7 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 56: | Zeile 56: | ||
{What is the maximum value of $p(t) = |z(t)|^2$ both in linear and logarithmic representation? | {What is the maximum value of $p(t) = |z(t)|^2$ both in linear and logarithmic representation? | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Max}\big[p(t)\big] \ = \ $ { | + | ${\rm Max}\big[p(t)\big] \ = \ $ { 4 3% } |
| − | ${\rm Max}\big [10 \cdot {\rm lg} \ p(t)\big] \ = \ $ { 6 3% } $ \ \rm dB$ | + | ${\rm Max}\big[10 \cdot {\rm lg} \ p(t)\big] \ = \ $ { 6 3% } $ \ \rm dB$ |
| − | {Let ${\rm Pr}\big[a(t) ≤ 1\big] = $0.394 Determine the Rayleigh | + | {Let ${\rm Pr}\big[a(t) ≤ 1\big] = $0.394 Determine the Rayleigh parameter $\sigma$. |
|type="{}"} | |type="{}"} | ||
$\sigma \ = \ $ { 1 3% } | $\sigma \ = \ $ { 1 3% } | ||
| − | {What is the probability | + | {What is the probability that the logarithmic Rayleigh coefficient $10 \cdot {\rm lg} \ p(t)$ is between $\text{-3 dB}$ and $\text{+3 dB}$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(|10 \cdot {\rm lg} \ p(t)| < 3 \ \rm dB) \ = \ $ { 0.411 3% } | ${\rm Pr}(|10 \cdot {\rm lg} \ p(t)| < 3 \ \rm dB) \ = \ $ { 0.411 3% } | ||
| Zeile 70: | Zeile 70: | ||
===Sample solution=== | ===Sample solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)'' From ${\rm Max}[a(t)] = 2$ follows directly: | + | '''(1)''' From ${\rm Max}[a(t)] = 2$ follows directly: |
| − | $${\rm Max} \left [ 20 \cdot {\rm lg}\hspace{0.15cm}a(t) \right ] = 20 \cdot {\rm lg}\hspace{0.15cm}(2) \hspace{0.15cm} \underline{\approx 6\,\,{\rm dB}} | + | :$${\rm Max} \left [ 20 \cdot {\rm lg}\hspace{0.15cm}a(t) \right ] = 20 \cdot {\rm lg}\hspace{0.15cm}(2) \hspace{0.15cm} \underline{\approx 6\,\,{\rm dB}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
'''(2)''' The maximum value of the square $p(t) = a(t)^2$ is | '''(2)''' The maximum value of the square $p(t) = a(t)^2$ is | ||
| − | + | $${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{=4} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The logarithmic representation of the | + | *The logarithmic representation of the squared magnitude $p(t)$ is identical to the logarithmic representation of the amount $a(t)$. Since $p(t)$ is a power quantity |
| − | $$ | + | :$${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{= 4} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 88: | Zeile 88: | ||
'''(3)''' The condition $a(t) ≤ 1$ is equivalent to the requirement $p(t) = a(t)^2 ≤ 1$. | '''(3)''' The condition $a(t) ≤ 1$ is equivalent to the requirement $p(t) = a(t)^2 ≤ 1$. | ||
| − | *The absolute square is known to be exponentially distributed, and for $p ≥ 0$ | + | *The absolute square is known to be exponentially distributed, and for $p ≥ 0$ we have |
$$f_p(p) = \frac{1}{2\sigma^2} \cdot {\rm exp} [ -\frac{p}{2\sigma^2}] | $$f_p(p) = \frac{1}{2\sigma^2} \cdot {\rm exp} [ -\frac{p}{2\sigma^2}] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | [[File: | + | [[File:EN_Mob_A_1_3_c.png|right|frame|PDF and probability regions ]] |
*It follows: | *It follows: | ||
| Zeile 100: | Zeile 100: | ||
\underline{\sigma = 1} \hspace{0.05cm}.$$ | \underline{\sigma = 1} \hspace{0.05cm}.$$ | ||
| − | The | + | The graph shows |
| − | * left the probability ${\rm Pr}(p(t) ≤ 1)$, | + | * on the left side the probability ${\rm Pr}(p(t) ≤ 1)$, |
| − | * right the probability ${\rm Pr}(0.5 \le p(t) ≤ 2)$. | + | * on the right side the probability ${\rm Pr}(0.5 \le p(t) ≤ 2)$. |
| − | '''(4)'' From $10 \cdot {\rm lg} \ p_1 = \ –3 \ \ \rm dB$ follows $p_1 = 0.5$ | + | '''(4)'' From $10 \cdot {\rm lg} \ p_1 = \ –3 \ \ \rm dB$ follows $p_1 = 0.5$. The upper limit of the integration range results from the condition $10 \cdot {\rm lg} \ p_2 = +3 \ \ \rm dB$, so $p_2 = 2$. |
| − | *This gives | + | *This gives, according to the above graph: |
$${\rm Pr}(-3\,\,{\rm dB}\le 10 \cdot {\rm lg}\hspace{0.15cm}p(t) \le +3\,\,{\rm dB}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0.5}^{2}f_p(p)\hspace{0.15cm}{\rm d}p = | $${\rm Pr}(-3\,\,{\rm dB}\le 10 \cdot {\rm lg}\hspace{0.15cm}p(t) \le +3\,\,{\rm dB}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0.5}^{2}f_p(p)\hspace{0.15cm}{\rm d}p = | ||
\left [ - {\rm e}^{ -{p}/(2\sigma^2)}\hspace{0.15cm} \right ]_{0.5}^{2} ={\rm e}^{-0.25}- {\rm e}^{-1} \approx 0.779 - 0.368 \hspace{0.15cm} \underline{ = 0.411} \hspace{0.05cm}.$$ | \left [ - {\rm e}^{ -{p}/(2\sigma^2)}\hspace{0.15cm} \right ]_{0.5}^{2} ={\rm e}^{-0.25}- {\rm e}^{-1} \approx 0.779 - 0.368 \hspace{0.15cm} \underline{ = 0.411} \hspace{0.05cm}.$$ | ||
Aktuelle Version vom 11. Mai 2020, 14:06 Uhr
Rayleigh–Fading should be used when
- there is no direct connection between transmitter and receiver, and
- the signal reaches the receiver through many paths, but their transit times are approximately the same.
An example of such a Rayleigh channel occurs in urban mobile communications when narrow-band signals are used with ranges between $50$ and $100$ meters.
Looking at the radio signals $s(t)$ and $r(t)$ in the equivalent low-pass range $($that is, around the frequency $f = 0)$, the signal transmission is described completely by the equation
- $$r(t)= z(t) \cdot s(t)$$
The multiplicative fading coefficient
- $$z(t)= x(t) + {\rm j} \cdot y(t)$$
is always complex and has the following characteristics:
- The real part $x(t)$ and the imaginary part $y(t)$ are Gaussian mean-free random variables, both with equal variance $\sigma^2$. Within the components $x(t)$ and $y(t)$ there may be statistical dependence, but this is not relevant for the solution of the present task. We assume that $x(t)$ and $y(t)$; are uncorrelated.
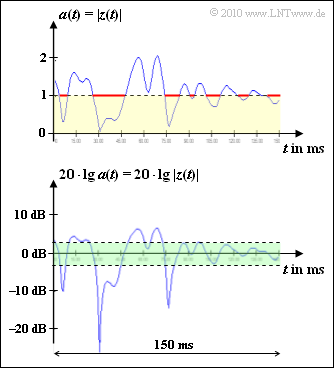
- The magnitude $a(t) = |z(t)|$ has a Rayleigh PDF, from which the name Rayleigh Fading is derived:
- $$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^ { -a^2/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm}.$$
- The squared magnitude $p(t) = a(t)^2 = |z(t)|^2$ is exponentially distributed according to the equation
- $$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^ { -p/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} \hspace{0.05cm}.$$
Measurements have shown that the time intervals with $a(t) ≤ 1$ (highlighted in yellow in the graphic) add up to $\text{59 ms}$ (intervals highlighted in red). Being the total measurement time $\text{150 ms}$, the probability that the magnitude of the Rayleigh fading is less than or equal to $1$ is $${\rm Pr}(a(t) \le 1) = \frac{59\,\,{\,{\rm ms}}}{150\,\,{\rm ms}} = 39.4 \% \hspace{0.05cm}.$$
In the lower graph, the value range between $\text{-3 dB}$ and $\text{+3 dB}$ of the logarithmic Rayleigh coefficient $20 \cdot {\rm lg} \ a(t)$ is highlighted in green. The subtask (4) refers to this.
Notes:
- This task belongs to chapter Wahrscheinlichkeitsdichte des Rayleigh–Fadings of this book.
- A similar topic is treated with a different approach in chapter Weitere Verteilungen of the book „Stochastic Signal Theory”.
- To check your results, you can use the interactive applet WDF, VTF and Moments of the book „Stochastic Signal Theory”.
Questionnaire
Sample solution
- $${\rm Max} \left [ 20 \cdot {\rm lg}\hspace{0.15cm}a(t) \right ] = 20 \cdot {\rm lg}\hspace{0.15cm}(2) \hspace{0.15cm} \underline{\approx 6\,\,{\rm dB}} \hspace{0.05cm}.$$
(2) The maximum value of the square $p(t) = a(t)^2$ is
$${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{=4}
\hspace{0.05cm}.$$
- The logarithmic representation of the squared magnitude $p(t)$ is identical to the logarithmic representation of the amount $a(t)$. Since $p(t)$ is a power quantity
- $${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{= 4} \hspace{0.05cm}.$$
- The maximum value is thus also $\underline{\approx 6\,\,{\rm dB}}$.
(3) The condition $a(t) ≤ 1$ is equivalent to the requirement $p(t) = a(t)^2 ≤ 1$.
- The absolute square is known to be exponentially distributed, and for $p ≥ 0$ we have
$$f_p(p) = \frac{1}{2\sigma^2} \cdot {\rm exp} [ -\frac{p}{2\sigma^2}] \hspace{0.05cm}.$$
- It follows:
$${\rm Pr}(p(t) \le 1) = \frac{1}{2\sigma^2} \cdot \int_{0}^{1}{\rm exp} [ -\frac{p}{2\sigma^2}] \hspace{0.15cm}{\rm d}p = 1 - {\rm exp} [ -\frac{1}{2\sigma^2}] = 0.394$$ $$\Rightarrow \hspace{0.3cm} {\rm exp} [ -\frac{1}{2\sigma^2}] = 0.606 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma^2 = \frac{1}{2 \cdot {\rm ln}\hspace{0.1cm}(0.606)} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{\sigma = 1} \hspace{0.05cm}.$$
The graph shows
- on the left side the probability ${\rm Pr}(p(t) ≤ 1)$,
- on the right side the probability ${\rm Pr}(0.5 \le p(t) ≤ 2)$.
'(4) From $10 \cdot {\rm lg} \ p_1 = \ –3 \ \ \rm dB$ follows $p_1 = 0.5$. The upper limit of the integration range results from the condition $10 \cdot {\rm lg} \ p_2 = +3 \ \ \rm dB$, so $p_2 = 2$.
- This gives, according to the above graph:
$${\rm Pr}(-3\,\,{\rm dB}\le 10 \cdot {\rm lg}\hspace{0.15cm}p(t) \le +3\,\,{\rm dB}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0.5}^{2}f_p(p)\hspace{0.15cm}{\rm d}p = \left [ - {\rm e}^{ -{p}/(2\sigma^2)}\hspace{0.15cm} \right ]_{0.5}^{2} ={\rm e}^{-0.25}- {\rm e}^{-1} \approx 0.779 - 0.368 \hspace{0.15cm} \underline{ = 0.411} \hspace{0.05cm}.$$