Aufgaben:Aufgabe 2.7Z: Kohärenzbandbreite des LZI–Zweiwegekanals: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 2.7Z BK für den LZI–Zweiwegekanal nach Aufgabe 2.7Z: BK für den LZI–Zweiwegekanal) |
|||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Das GWSSUS–Kanalmodell}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Das GWSSUS–Kanalmodell}} | ||
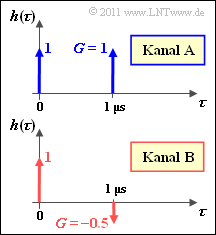
| − | [[Datei:P_ID2178__Mob_Z_2_7.png|right|frame|Zweiwegekanäle]] | + | [[Datei:P_ID2178__Mob_Z_2_7.png|right|frame|Zwei Zweiwegekanäle]] |
| − | Zum GWSSUS–Modell werden zwei Kenngrößen angegeben, die beide die entstehende Verzögerung $\tau$ statistisch erfassen. Mehr Informationen zum Thema „Mehrwegeausbreitung” finden Sie | + | Zum GWSSUS–Modell werden zwei Kenngrößen angegeben, die beide die entstehende Verzögerung $\tau$ statistisch erfassen. Mehr Informationen zum Thema „Mehrwegeausbreitung” finden Sie im Abschnitt [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell#Simulation_gem.C3.A4.C3.9F_dem_GWSSUS.E2.80.93Modell| Simulation gemäß dem GWSSUS–Modell]] des Theorieteils. |
| − | * Die <b>Mehrwegeverbreiterung</b> $T_{\rm V}$ ist definitionsgemäß gleich der Standardabweichung der Zufallsgröße $\tau$. Diese kann aus der Wahrscheinlichkeitsdichte $f_{\rm V}(\tau)$ ermittelt werden. Die WDF $f_{\rm V}(\tau)$ ist dabei formgleich mit dem Verzögerungs–Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$ | + | * Die <b>Mehrwegeverbreiterung</b> $T_{\rm V}$ ist definitionsgemäß gleich der Standardabweichung der Zufallsgröße $\tau$. <br>Diese kann aus der Wahrscheinlichkeitsdichte $f_{\rm V}(\tau)$ ermittelt werden. Die WDF $f_{\rm V}(\tau)$ ist dabei formgleich mit dem Verzögerungs–Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$. |
| − | * Die <b>Kohärenzbandbreite</b> $B_{\rm K}$ beschreibt den gleichen Sachverhalt im Frequenzbereich. Diese ist implizit durch die | + | * Die <b>Kohärenzbandbreite</b> $B_{\rm K}$ beschreibt den gleichen Sachverhalt im Frequenzbereich. <br>Diese ist implizit durch die Frequenz–Korrelationsfunktion $\varphi_{\rm F}(\Delta f)$ festgelegt als derjenige $\Delta f$–Wert, bei dem deren Betrag erstmals auf die Hälfte abgefallen ist: |
| − | :$$|\varphi_{\rm F}(\Delta f = B_{\rm K})| \stackrel {!}{=} | + | :$$|\varphi_{\rm F}(\Delta f = B_{\rm K})| \stackrel {!}{=} {1}/{2} \cdot |\varphi_{\rm F}(\Delta f = 0)| \hspace{0.05cm}.$$ |
| − | Der Zusammenhang zwischen ${\it \Phi}_{\rm V}(\tau)$ und $\varphi_{\rm F}(\Delta f)$ ist durch die Fouriertransformation gegeben: | + | Der Zusammenhang zwischen ${\it \Phi}_{\rm V}(\tau)$ und $\varphi_{\rm F}(\Delta f)$ ist durch die Fouriertransformation gegeben: |
:$$\varphi_{\rm F}(\Delta f) | :$$\varphi_{\rm F}(\Delta f) | ||
\hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$ | \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$ | ||
| − | Beide Definitionen sind bei einem zeitinvarianten Kanal nur bedingt geeignet. | + | *Beide Definitionen sind bei einem zeitinvarianten Kanal nur bedingt geeignet. |
| − | :$$B_{\rm K}\hspace{0. | + | *Oft verwendet man für einen zeitinvarianten Zweiwegekanal (also mit konstanten Pfadgewichten entsprechend obiger Grafik) als Näherung für die Kohärenzbandbreite: |
| + | :$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$ | ||
| + | |||
In dieser Aufgabe soll geklärt werden, | In dieser Aufgabe soll geklärt werden, | ||
* warum es in der Literatur verschiedene Definitionen für die Kohärenzbandbreite gibt, | * warum es in der Literatur verschiedene Definitionen für die Kohärenzbandbreite gibt, | ||
| − | * welcher Zusammenhang zwischen $B_{\rm K}$ und $B_{\rm K}'$ besteht, und | + | * welcher Zusammenhang zwischen $B_{\rm K}$ und $B_{\rm K}\hspace{0.01cm}'$ besteht, und |
* welche Definitionen bei welchen Randbedingungen sinnvoll sind. | * welche Definitionen bei welchen Randbedingungen sinnvoll sind. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe | + | *Die Aufgabe gehört zum Kapitel [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell| Das GWSSUS–Kanalmodell]]. |
| − | * | + | *Bezug genommen wird auch auf einige Theorieseiten im Kapitel [[Mobile_Kommunikation/Mehrwegeempfang_beim_Mobilfunk| Mehrwegeempfang beim Mobilfunk]]. |
| + | |||
| Zeile 29: | Zeile 39: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Kohärenzbandbreitennäherungen ergeben sich für Kanal A und B? | + | {Welche Kohärenzbandbreitennäherungen $B_{\rm K}\hspace{0.01cm}'$ ergeben sich für den Kanal $\rm A$ und den Kanal $\rm B$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm | + | Kanal ${\rm A} \text {:} \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' \ = \ ${ 1000 3% } $\ \rm kHz$ |
| − | ${\rm | + | Kanal ${\rm B} \text {:} \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' \ = \ ${ 1000 3% } $\ \rm kHz$ |
| − | {Wie lautet die WDF $f_{\rm V}(\tau)$? $G$ | + | {Wie lautet die WDF $f_{\rm V}(\tau)$? Hierbei gibt $G$ das Gewicht des zweiten Pfades an. |
| − | |type=" | + | |type="()"} |
- $f_{\rm V}(\tau) = \delta(\tau) + G \cdot \delta(\tau \, –\tau_0)$, | - $f_{\rm V}(\tau) = \delta(\tau) + G \cdot \delta(\tau \, –\tau_0)$, | ||
- $f_{\rm V}(\tau) = \delta(\tau) + G^2 \cdot \delta(\tau \, –\tau_0)$, | - $f_{\rm V}(\tau) = \delta(\tau) + G^2 \cdot \delta(\tau \, –\tau_0)$, | ||
+ $f_{\rm V}(\tau) = 1/(1 + G^2) \cdot \delta(\tau) + G^2/(1 + G^2) \cdot \delta(\tau \, –\tau_0)$. | + $f_{\rm V}(\tau) = 1/(1 + G^2) \cdot \delta(\tau) + G^2/(1 + G^2) \cdot \delta(\tau \, –\tau_0)$. | ||
| − | {Berechnen Sie die Mehrwegeverbreitung. | + | {Berechnen Sie die Mehrwegeverbreitung $ T_{\rm V}$. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm | + | Kanal ${\rm A} \text{:} \hspace{0.4cm} T_{\rm V} \ = \ ${ 0.5 3% } $\ \rm µ s$ |
| − | ${\rm | + | Kanal ${\rm B} \text{:} \hspace{0.4cm} T_{\rm V} \ = \ ${ 0.4 3% } $\ \rm µ s$ |
| − | {Welche Kohärenzbandbreite $B_{\rm K}$ weist der Kanal A auf? | + | {Welche Kohärenzbandbreite $B_{\rm K}$ weist der Kanal ${\rm A}$ auf? |
| − | |type=" | + | |type="()"} |
| − | + Es gilt $B_{\rm K} = 333 \ \rm kHz$. | + | + Es gilt $B_{\rm K} = 333 \ \rm kHz$. |
| − | - Es gilt $B_{\rm K} = 500 \ \rm kHz$. | + | - Es gilt $B_{\rm K} = 500 \ \rm kHz$. |
| − | - Es gilt $B_{\rm K} = 1 \ \rm MHz$. | + | - Es gilt $B_{\rm K} = 1 \ \rm MHz$. |
| − | - $B_{\rm K}$ ist nach dieser Definition nicht angebbar. | + | - $B_{\rm K}$ ist nach dieser Definition nicht angebbar. |
| − | {Welche Kohärenzbandbreite $B_{\rm K}$ weist der Kanal B auf? | + | {Welche Kohärenzbandbreite $B_{\rm K}$ weist der Kanal ${\rm B}$ auf? |
| − | |type=" | + | |type="()"} |
| − | - Es gilt $B_{\rm K} = 333 \ \rm kHz$. | + | - Es gilt $B_{\rm K} = 333 \ \rm kHz$. |
| − | - Es gilt $B_{\rm K} = 500 \ \rm kHz$. | + | - Es gilt $B_{\rm K} = 500 \ \rm kHz$. |
| − | - Es gilt $B_{\rm K} = 1 \ \rm MHz$. | + | - Es gilt $B_{\rm K} = 1 \ \rm MHz$. |
| − | + $B_{\rm K}$ ist nach dieser Definition nicht angebbar. | + | + $B_{\rm K}$ ist nach dieser Definition nicht angebbar. |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Bei beiden Kanälen beträgt Laufzeitdifferenz $\Delta \tau = \tau_{\rm max} \, | + | '''(1)''' Bei beiden Kanälen beträgt die Laufzeitdifferenz $\Delta \tau = \tau_{\rm max} \, - \tau_{\rm min} = 1 \ \rm µ s$. |
| + | * Deshalb ergibt sich bei beiden Kanälen der gleiche Wert: | ||
| + | :$$B_{\rm K}\hspace{0.01cm}' \ \underline {= 1000 \ \rm kHz}.$$ | ||
| − | '''(2)''' Die Grafiken beziehen sich auf die Impulsantwort $h(\tau)$. Um das Verzögerungs–LDS zu erhalten, müssen die Gewichte quadriert werden: | + | |
| + | '''(2)''' Die Grafiken beziehen sich auf die Impulsantwort $h(\tau)$. | ||
| + | *Um das Verzögerungs–LDS zu erhalten, müssen die Gewichte quadriert werden: | ||
:$${\it \Phi}_{\rm V}(\tau) = 1^2 \cdot \delta(\tau) + G^2 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$ | :$${\it \Phi}_{\rm V}(\tau) = 1^2 \cdot \delta(\tau) + G^2 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$ | ||
| − | Das Integral über ${\it \Phi}_{\rm V}(\tau)$ ist demnach $1 + G^2$. Die Wahrscheinlichkeitsdichtefunktion (WDF) muss aber die „Fläche 1” ergeben (Summe der beiden Diracgewichte gleich $1$ | + | *Das Integral über ${\it \Phi}_{\rm V}(\tau)$ ist demnach $1 + G^2$. |
| + | *Die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ muss aber die „Fläche 1” ergeben $($Summe der beiden Diracgewichte gleich $1)$. Daraus folgt: | ||
:$$f_{\rm V}(\tau) = \frac{1}{1 + G^2} \cdot \delta(\tau) + \frac{G^2}{1 + G^2} \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$ | :$$f_{\rm V}(\tau) = \frac{1}{1 + G^2} \cdot \delta(\tau) + \frac{G^2}{1 + G^2} \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$ | ||
| − | Richtig ist somit nur der <u>Lösungsvorschlag 3</u>. Der erste Vorschlag beschreibt nicht die WDF $f_{\rm V}(\tau)$, sondern die | + | *Richtig ist somit nur der <u>Lösungsvorschlag 3</u>. |
| + | *Der erste Vorschlag beschreibt nicht die WDF $f_{\rm V}(\tau)$, sondern die Impulsantwort $h(\tau)$. | ||
| + | *Die zweite Gleichung gibt das Verzögerungs–LDS ${\it \Phi}_{\rm V}(\tau)$ an. | ||
| + | |||
| + | |||
| − | '''(3)''' Beim Kanal A sind die beiden Impulsgewichte gleich. Damit kann für den Mittelwert $m_{\rm V}$ und die Standardabweichung $\sigma_{\rm V} = T_{\rm V}$ ohne große Rechnung geschrieben werden: | + | '''(3)''' Beim Kanal $\rm A$ sind die beiden Impulsgewichte gleich. |
| − | :$$m_{\rm V} = \frac{\tau_0}{2} \hspace{0.15cm} {= 0.5\,{\rm | + | *Damit kann für den Mittelwert $m_{\rm V}$ und die Standardabweichung $\sigma_{\rm V} = T_{\rm V}$ ohne große Rechnung geschrieben werden: |
| − | \hspace{0.2cm}T_{\rm V} = \sigma_{\rm V} =\frac{\tau_0}{2} \hspace{0.15cm}\underline {= 0.5\,{\rm | + | :$$m_{\rm V} = \frac{\tau_0}{2} \hspace{0.15cm} {= 0.5\,{\rm µ s}}\hspace{0.05cm}, |
| + | \hspace{0.2cm}T_{\rm V} = \sigma_{\rm V} =\frac{\tau_0}{2} \hspace{0.15cm}\underline {= 0.5\,{\rm µ s}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Beim Kanal B sind die Impulsgewichte $1/(1+0.5^2) = 0.8$ (für $\tau = 0$ | + | Beim Kanal $\rm B$ sind die Impulsgewichte $1/(1+0.5^2) = 0.8$ $($für $\tau = 0)$ und $0.2$ $($für $\tau = 1 \ \rm µ s)$. |
| − | :$$m_{\rm 1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \cdot 0 + 0.2 \cdot 1\,{\rm | + | * Damit erhält man für den linearen und den quadratischen Mittelwert nach den [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Momentenberechnung_als_Scharmittelwert|grundlegenden Gesetzen]] der Statistik: |
| − | + | :$$m_{\rm 1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \cdot 0 + 0.2 \cdot 1\,{\rm µ s} = 0.2\,{\rm µ s} \hspace{0.05cm},\hspace{0.5cm} | |
| + | m_{\rm 2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \cdot 0^2 + 0.2 \cdot (1\,{\rm µ s})^2 = 0.2\,({\rm µ s})^2 \hspace{0.05cm}.$$ | ||
| − | Zum gesuchten Ergebnis kommt man mit dem [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Einige_h.C3.A4ufig_benutzte_Zentralmomente| Satz von Steiner]] | + | *Zum gesuchten Ergebnis kommt man mit dem [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Einige_h.C3.A4ufig_benutzte_Zentralmomente| Satz von Steiner]]: |
| − | :$$\sigma_{\rm V}^2 = m_{\rm 2} - m_{\rm 1}^2 = 0.2\,({\rm | + | :$$\sigma_{\rm V}^2 = m_{\rm 2} - m_{\rm 1}^2 = 0.2\,({\rm µ s})^2 - (0.2\,{\rm µ s})^2 = 0.16\,({\rm µ s})^2 |
| − | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {= 0.4\,{\rm | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {= 0.4\,{\rm µ s}}\hspace{0.05cm}.$$ |
| − | '''(4)''' Die | + | |
| + | '''(4)''' Die Frequenz–Korrelationsfunktion ist die Fouriertransformierte von ${\it \Phi}_{\rm V}(\tau) = \delta(\tau) + \delta(\tau \, - \tau_0)$: | ||
:$$\varphi_{\rm F}(\Delta f) = 1 + {\rm exp}(-{\rm j} \cdot 2\pi \cdot \Delta f \cdot \tau_0) = 1 + {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) -{\rm j} \cdot {\rm sin}(2\pi \cdot \Delta f \cdot \tau_0) $$ | :$$\varphi_{\rm F}(\Delta f) = 1 + {\rm exp}(-{\rm j} \cdot 2\pi \cdot \Delta f \cdot \tau_0) = 1 + {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) -{\rm j} \cdot {\rm sin}(2\pi \cdot \Delta f \cdot \tau_0) $$ | ||
| + | [[Datei:P_ID2186__Mob_Z_2_7d.png|right|frame|Frequenzkorrelationsfunktion und Kohärenzbandbreite]] | ||
:$$\Rightarrow \hspace{0.3cm} |\varphi_{\rm F}(\Delta f)| = \sqrt{2 + 2 \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) }\hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} |\varphi_{\rm F}(\Delta f)| = \sqrt{2 + 2 \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) }\hspace{0.05cm}.$$ | ||
| − | Das Funktionsmaximum bei $\Delta f = 0$ ist gleich $2$. Deshalb lautet die Bestimmungsgleichung für $B_{\rm K}$: | + | *Das Funktionsmaximum bei $\Delta f = 0$ ist gleich $2$. |
| − | :$$|\varphi_{\rm F}(B_{\rm K})| = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}|\varphi_{\rm F}(B_{\rm K})|^2 = 1 | + | *Deshalb lautet die Bestimmungsgleichung für $B_{\rm K}$: |
| + | :$$|\varphi_{\rm F}(B_{\rm K})| = 1 \hspace{0.3cm} $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}|\varphi_{\rm F}(B_{\rm K})|^2 = 1 | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm}2 + 2 \cdot {\rm cos}(2\pi \cdot B_{\rm K} \cdot \tau_0) = 1$$ | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}2 + 2 \cdot {\rm cos}(2\pi \cdot B_{\rm K} \cdot \tau_0) = 1$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm}{\rm cos}(2\pi \cdot B_{\rm K} \cdot \tau_0) = -0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}2\pi \cdot B_{\rm K} \cdot \tau_0 = \frac{2\pi}{3}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}B_{\rm K} = \frac{1}{3\tau_0} = 333\,{\rm kHz}\hspace{0.05cm}.$$ | + | :$$\Rightarrow \hspace{0.3cm}{\rm cos}(2\pi \cdot B_{\rm K} \cdot \tau_0) = -0.5 \hspace{0.3cm} $$ |
| + | :$$\Rightarrow \hspace{0.3cm}2\pi \cdot B_{\rm K} \cdot \tau_0 = \frac{2\pi}{3}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}B_{\rm K} = \frac{1}{3\tau_0} = 333\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| + | |||
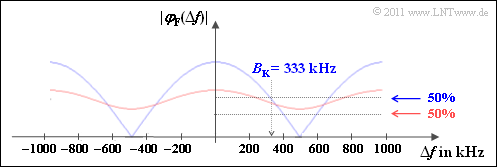
| + | *Richtig ist somit der <u>Lösungsvorschlag 1</u>. Die Grafik (blaue Kurve) verdeutlicht das Ergebnis. | ||
| − | |||
| − | |||
| + | '''(5)''' Für den Kanal ${\rm B}$ lauten die entsprechenden Gleichungen: | ||
| + | :$${\it \Phi}_{\rm V}(\tau) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1^2 \cdot \delta(\tau) + (-0.5)^2 \cdot \delta(\tau - \tau_0) \hspace{0.05cm},\hspace{0.05cm} | ||
| + | \varphi_{\rm F}(\Delta f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + 0.25 \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) -{\rm j} \cdot 0.25 \cdot {\rm sin}(2\pi \cdot \Delta f \cdot \tau_0)\hspace{0.05cm},$$ | ||
| + | :$$|\varphi_{\rm F}(\Delta f)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm}= \sqrt{\frac{17}{16} + \frac{1}{2} \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) }\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}{\rm Max}\hspace{0.1cm}|\varphi_{\rm F}(\Delta f)| = 1.25\hspace{0.05cm},\hspace{0.2cm}{\rm Min}\hspace{0.1cm}|\varphi_{\rm F}(\Delta f)| = 0.75\hspace{0.05cm}.$$ | ||
| − | + | *Man erkennt an diesem Resultat, dass hier die $50\%$–Kohärenzbandbreite nicht angebbar ist. | |
| − | + | *Richtig ist also der <u>Lösungsvorschlag 4</u>. | |
| − | |||
| − | |||
| − | |||
| − | |||
Dieses Ergebnis ist der Grund dafür, dass es für die Kohärenzbandbreite in der Literatur unterschiedliche Definitionen gibt, zum Beispiel: | Dieses Ergebnis ist der Grund dafür, dass es für die Kohärenzbandbreite in der Literatur unterschiedliche Definitionen gibt, zum Beispiel: | ||
| − | * die $90\%$–Kohärenzbandbreite ($B_{\rm K, \ 90\%} | + | * die $90\%$–Kohärenzbandbreite $($im Beispiel wäre $B_{\rm K, \hspace{0.03cm} 90\%} =184 \ \rm kHz)$, |
| − | * die vorne angegebene sehr einfache Näherung $B_{\rm K}'$ (im Beispiel $1 \ \rm MHz$ | + | * die vorne angegebene sehr einfache Näherung $B_{\rm K}\hspace{0.01cm}'$ wäre $($im Beispiel $B_{\rm K}\hspace{0.01cm}' =1 \ \rm MHz)$. |
| − | Man erkennt bereits an diesen Zahlenwerten, dass alle diesbezüglichen Angaben sehr vage sind und sich die einzelnen „Kohärenzbandbreiten” um Faktoren unterscheiden können. | + | Man erkennt bereits an diesen doch sehr unterschiedlichen Zahlenwerten, dass alle diesbezüglichen Angaben sehr vage sind und sich die einzelnen „Kohärenzbandbreiten” um Faktoren unterscheiden können. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 4. Juni 2020, 16:32 Uhr
Zum GWSSUS–Modell werden zwei Kenngrößen angegeben, die beide die entstehende Verzögerung $\tau$ statistisch erfassen. Mehr Informationen zum Thema „Mehrwegeausbreitung” finden Sie im Abschnitt Simulation gemäß dem GWSSUS–Modell des Theorieteils.
- Die Mehrwegeverbreiterung $T_{\rm V}$ ist definitionsgemäß gleich der Standardabweichung der Zufallsgröße $\tau$.
Diese kann aus der Wahrscheinlichkeitsdichte $f_{\rm V}(\tau)$ ermittelt werden. Die WDF $f_{\rm V}(\tau)$ ist dabei formgleich mit dem Verzögerungs–Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$. - Die Kohärenzbandbreite $B_{\rm K}$ beschreibt den gleichen Sachverhalt im Frequenzbereich.
Diese ist implizit durch die Frequenz–Korrelationsfunktion $\varphi_{\rm F}(\Delta f)$ festgelegt als derjenige $\Delta f$–Wert, bei dem deren Betrag erstmals auf die Hälfte abgefallen ist:
- $$|\varphi_{\rm F}(\Delta f = B_{\rm K})| \stackrel {!}{=} {1}/{2} \cdot |\varphi_{\rm F}(\Delta f = 0)| \hspace{0.05cm}.$$
Der Zusammenhang zwischen ${\it \Phi}_{\rm V}(\tau)$ und $\varphi_{\rm F}(\Delta f)$ ist durch die Fouriertransformation gegeben:
- $$\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$
- Beide Definitionen sind bei einem zeitinvarianten Kanal nur bedingt geeignet.
- Oft verwendet man für einen zeitinvarianten Zweiwegekanal (also mit konstanten Pfadgewichten entsprechend obiger Grafik) als Näherung für die Kohärenzbandbreite:
- $$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$
In dieser Aufgabe soll geklärt werden,
- warum es in der Literatur verschiedene Definitionen für die Kohärenzbandbreite gibt,
- welcher Zusammenhang zwischen $B_{\rm K}$ und $B_{\rm K}\hspace{0.01cm}'$ besteht, und
- welche Definitionen bei welchen Randbedingungen sinnvoll sind.
Hinweise:
- Die Aufgabe gehört zum Kapitel Das GWSSUS–Kanalmodell.
- Bezug genommen wird auch auf einige Theorieseiten im Kapitel Mehrwegeempfang beim Mobilfunk.
Fragebogen
Musterlösung
- Deshalb ergibt sich bei beiden Kanälen der gleiche Wert:
- $$B_{\rm K}\hspace{0.01cm}' \ \underline {= 1000 \ \rm kHz}.$$
(2) Die Grafiken beziehen sich auf die Impulsantwort $h(\tau)$.
- Um das Verzögerungs–LDS zu erhalten, müssen die Gewichte quadriert werden:
- $${\it \Phi}_{\rm V}(\tau) = 1^2 \cdot \delta(\tau) + G^2 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$
- Das Integral über ${\it \Phi}_{\rm V}(\tau)$ ist demnach $1 + G^2$.
- Die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ muss aber die „Fläche 1” ergeben $($Summe der beiden Diracgewichte gleich $1)$. Daraus folgt:
- $$f_{\rm V}(\tau) = \frac{1}{1 + G^2} \cdot \delta(\tau) + \frac{G^2}{1 + G^2} \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$
- Richtig ist somit nur der Lösungsvorschlag 3.
- Der erste Vorschlag beschreibt nicht die WDF $f_{\rm V}(\tau)$, sondern die Impulsantwort $h(\tau)$.
- Die zweite Gleichung gibt das Verzögerungs–LDS ${\it \Phi}_{\rm V}(\tau)$ an.
(3) Beim Kanal $\rm A$ sind die beiden Impulsgewichte gleich.
- Damit kann für den Mittelwert $m_{\rm V}$ und die Standardabweichung $\sigma_{\rm V} = T_{\rm V}$ ohne große Rechnung geschrieben werden:
- $$m_{\rm V} = \frac{\tau_0}{2} \hspace{0.15cm} {= 0.5\,{\rm µ s}}\hspace{0.05cm}, \hspace{0.2cm}T_{\rm V} = \sigma_{\rm V} =\frac{\tau_0}{2} \hspace{0.15cm}\underline {= 0.5\,{\rm µ s}} \hspace{0.05cm}.$$
Beim Kanal $\rm B$ sind die Impulsgewichte $1/(1+0.5^2) = 0.8$ $($für $\tau = 0)$ und $0.2$ $($für $\tau = 1 \ \rm µ s)$.
- Damit erhält man für den linearen und den quadratischen Mittelwert nach den grundlegenden Gesetzen der Statistik:
- $$m_{\rm 1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \cdot 0 + 0.2 \cdot 1\,{\rm µ s} = 0.2\,{\rm µ s} \hspace{0.05cm},\hspace{0.5cm} m_{\rm 2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \cdot 0^2 + 0.2 \cdot (1\,{\rm µ s})^2 = 0.2\,({\rm µ s})^2 \hspace{0.05cm}.$$
- Zum gesuchten Ergebnis kommt man mit dem Satz von Steiner:
- $$\sigma_{\rm V}^2 = m_{\rm 2} - m_{\rm 1}^2 = 0.2\,({\rm µ s})^2 - (0.2\,{\rm µ s})^2 = 0.16\,({\rm µ s})^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {= 0.4\,{\rm µ s}}\hspace{0.05cm}.$$
(4) Die Frequenz–Korrelationsfunktion ist die Fouriertransformierte von ${\it \Phi}_{\rm V}(\tau) = \delta(\tau) + \delta(\tau \, - \tau_0)$:
- $$\varphi_{\rm F}(\Delta f) = 1 + {\rm exp}(-{\rm j} \cdot 2\pi \cdot \Delta f \cdot \tau_0) = 1 + {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) -{\rm j} \cdot {\rm sin}(2\pi \cdot \Delta f \cdot \tau_0) $$
- $$\Rightarrow \hspace{0.3cm} |\varphi_{\rm F}(\Delta f)| = \sqrt{2 + 2 \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) }\hspace{0.05cm}.$$
- Das Funktionsmaximum bei $\Delta f = 0$ ist gleich $2$.
- Deshalb lautet die Bestimmungsgleichung für $B_{\rm K}$:
- $$|\varphi_{\rm F}(B_{\rm K})| = 1 \hspace{0.3cm} $$
- $$\Rightarrow \hspace{0.3cm}|\varphi_{\rm F}(B_{\rm K})|^2 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}2 + 2 \cdot {\rm cos}(2\pi \cdot B_{\rm K} \cdot \tau_0) = 1$$
- $$\Rightarrow \hspace{0.3cm}{\rm cos}(2\pi \cdot B_{\rm K} \cdot \tau_0) = -0.5 \hspace{0.3cm} $$
- $$\Rightarrow \hspace{0.3cm}2\pi \cdot B_{\rm K} \cdot \tau_0 = \frac{2\pi}{3}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}B_{\rm K} = \frac{1}{3\tau_0} = 333\,{\rm kHz}\hspace{0.05cm}.$$
- Richtig ist somit der Lösungsvorschlag 1. Die Grafik (blaue Kurve) verdeutlicht das Ergebnis.
(5) Für den Kanal ${\rm B}$ lauten die entsprechenden Gleichungen:
- $${\it \Phi}_{\rm V}(\tau) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1^2 \cdot \delta(\tau) + (-0.5)^2 \cdot \delta(\tau - \tau_0) \hspace{0.05cm},\hspace{0.05cm} \varphi_{\rm F}(\Delta f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + 0.25 \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) -{\rm j} \cdot 0.25 \cdot {\rm sin}(2\pi \cdot \Delta f \cdot \tau_0)\hspace{0.05cm},$$
- $$|\varphi_{\rm F}(\Delta f)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm}= \sqrt{\frac{17}{16} + \frac{1}{2} \cdot {\rm cos}(2\pi \cdot \Delta f \cdot \tau_0) }\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Max}\hspace{0.1cm}|\varphi_{\rm F}(\Delta f)| = 1.25\hspace{0.05cm},\hspace{0.2cm}{\rm Min}\hspace{0.1cm}|\varphi_{\rm F}(\Delta f)| = 0.75\hspace{0.05cm}.$$
- Man erkennt an diesem Resultat, dass hier die $50\%$–Kohärenzbandbreite nicht angebbar ist.
- Richtig ist also der Lösungsvorschlag 4.
Dieses Ergebnis ist der Grund dafür, dass es für die Kohärenzbandbreite in der Literatur unterschiedliche Definitionen gibt, zum Beispiel:
- die $90\%$–Kohärenzbandbreite $($im Beispiel wäre $B_{\rm K, \hspace{0.03cm} 90\%} =184 \ \rm kHz)$,
- die vorne angegebene sehr einfache Näherung $B_{\rm K}\hspace{0.01cm}'$ wäre $($im Beispiel $B_{\rm K}\hspace{0.01cm}' =1 \ \rm MHz)$.
Man erkennt bereits an diesen doch sehr unterschiedlichen Zahlenwerten, dass alle diesbezüglichen Angaben sehr vage sind und sich die einzelnen „Kohärenzbandbreiten” um Faktoren unterscheiden können.