Aufgaben:Aufgabe 1.3: Gemessene Sprungantwort: Unterschied zwischen den Versionen
Tasnad (Diskussion | Beiträge) |
|||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 31: | Zeile 31: | ||
*Für den Rechteckimpuls $x_2(t)$ kann mit $A = 2 \hspace{0.05cm} \text{V}$ auch geschrieben werden: | *Für den Rechteckimpuls $x_2(t)$ kann mit $A = 2 \hspace{0.05cm} \text{V}$ auch geschrieben werden: | ||
:$$x_2(t) = A \cdot \big [\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big ].$$ | :$$x_2(t) = A \cdot \big [\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big ].$$ | ||
| − | *Der Frequenzgang $H(f)$ des hier betrachteten LZI–Systems kann dem Angabenblatt zu [[Aufgaben:Aufgabe_3.8:_Dreimal_Faltung | + | *Der Frequenzgang $H(f)$ des hier betrachteten LZI–Systems kann dem Angabenblatt zu [[Aufgaben:Aufgabe_3.8:_Dreimal_Faltung|Aufgabe 3.8]] im Buch „Signaldarstellung” entnommen werden. Allerdings sind die Abszissen– und Ordinatenparameter entsprechend anzupassen. |
*Zur Lösung der vorliegenden Aufgabe wird $H(f)$ jedoch nicht explizit benötigt. | *Zur Lösung der vorliegenden Aufgabe wird $H(f)$ jedoch nicht explizit benötigt. | ||
| Zeile 77: | Zeile 77: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | '''(1)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | ||
| − | *Für das Ausgangssignal gilt $y_1(t)=0$, solange das Eingangssignal $x_1(t) = 0$. Das bedeutet, dass hier ein kausales System vorliegt. | + | *Für das Ausgangssignal gilt $y_1(t)=0$, solange das Eingangssignal $x_1(t) = 0$ ist. Das bedeutet, dass hier ein kausales System vorliegt. |
*Zum gleichen Ergebnis hätte man allein durch die Aussage „das Ausgangssignal wurde gemessen” kommen können. Nur kausale Systeme sind realisierbar und nur bei realisierbaren Systemen kann etwas gemessen werden. | *Zum gleichen Ergebnis hätte man allein durch die Aussage „das Ausgangssignal wurde gemessen” kommen können. Nur kausale Systeme sind realisierbar und nur bei realisierbaren Systemen kann etwas gemessen werden. | ||
| − | *Das Eingangssignal $x_1(t)$ kann für sehr große Zeiten $(t \gg 0)$ als Gleichsignal interpretiert werden. Wäre $H(f)$ ein Hochpass, dann müsste $y_1(t)$ für $t → ∞$ gegen Null gehen. Das heißt: $H(f)$ stellt einen Tiefpass dar. | + | *Das Eingangssignal $x_1(t)$ kann für sehr große Zeiten $(t \gg 0)$ als Gleichsignal interpretiert werden. Wäre $H(f)$ ein Hochpass, dann müsste $y_1(t)$ für $t → ∞$ gegen Null gehen. Das heißt: $H(f)$ stellt einen Tiefpass dar. |
| − | '''(2)''' Der Gleichsignalübertragungsfaktor kann aus $x_1(t)$ und $y_1(t)$ abgelesen werden, wenn der Einschwingvorgang abgeklungen ist: | + | |
| + | '''(2)''' Der Gleichsignalübertragungsfaktor kann aus $x_1(t)$ und $y_1(t)$ abgelesen werden, wenn der Einschwingvorgang abgeklungen ist: | ||
:$$H(f =0) = \frac{y_1(t \rightarrow \infty)}{x_1(t \rightarrow \infty)}= | :$$H(f =0) = \frac{y_1(t \rightarrow \infty)}{x_1(t \rightarrow \infty)}= | ||
\frac{ {\rm 1\, V} }{ {\rm 4\, V} } \hspace{0.15cm}\underline{= 0.25}.$$ | \frac{ {\rm 1\, V} }{ {\rm 4\, V} } \hspace{0.15cm}\underline{= 0.25}.$$ | ||
| − | '''(3)''' Die Sprungantwort $σ(t)$ ist gleich dem Ausgangssignal $y(t)$, wenn am Eingang $x(t) = γ(t)$ anliegen würde. | + | |
| − | *Wegen $x_1(t) = 4 \hspace{0.05cm} \rm {V} · γ(t)$ gilt somit im Bereich von $0$ bis $T = 2 \ \rm ms$: | + | '''(3)''' Die Sprungantwort $σ(t)$ ist gleich dem Ausgangssignal $y(t)$, wenn am Eingang $x(t) = γ(t)$ anliegen würde. |
| + | *Wegen $x_1(t) = 4 \hspace{0.05cm} \rm {V} · γ(t)$ gilt somit im Bereich von $0$ bis $T = 2 \ \rm ms$: | ||
:$$\sigma(t) = \frac{y_1(t)}{ {\rm 4\, V} } = 0.5 \cdot\big( {t}/{T} - 0.5 ({t}/{T})^2\big).$$ | :$$\sigma(t) = \frac{y_1(t)}{ {\rm 4\, V} } = 0.5 \cdot\big( {t}/{T} - 0.5 ({t}/{T})^2\big).$$ | ||
| − | *Zum Zeitpunkt $t = T = 2 \ \rm ms$ erreicht die Sprungantwort ihren Endwert $0.25$. | + | *Zum Zeitpunkt $t = T = 2 \ \rm ms$ erreicht die Sprungantwort ihren Endwert $0.25$. |
| − | *Für $t = T/2 = 1 \ \rm ms$ ergibt sich der Zahlenwert $3/16 \; \underline{\: = \: 0.1875}$. | + | *Für $t = T/2 = 1 \ \rm ms$ ergibt sich der Zahlenwert $3/16 \; \underline{\: = \: 0.1875}$. |
| − | *Beachten Sie bitte, dass die Sprungantwort $σ(t)$ ebenso wie die Sprungfunktion $γ(t)$ keine Einheit besitzt. | + | *Beachten Sie bitte, dass die Sprungantwort $σ(t)$ ebenso wie die Sprungfunktion $γ(t)$ keine Einheit besitzt. |
| + | |||
[[Datei:P_ID840__LZI_A_1_3d.png |Berechnete Impulsantwort | rechts|frame]] | [[Datei:P_ID840__LZI_A_1_3d.png |Berechnete Impulsantwort | rechts|frame]] | ||
| − | '''(4)''' Die Sprungantwort $σ(t)$ ist das Integral über die Impulsantwort $h(t)$. Damit ergibt sich $h(t)$ aus $σ(t)$ durch Differentiation nach der Zeit. Im Bereich $0 < t < T$ gilt deshalb: | + | '''(4)''' Die Sprungantwort $σ(t)$ ist das Integral über die Impulsantwort $h(t)$. |
| + | *Damit ergibt sich $h(t)$ aus $σ(t)$ durch Differentiation nach der Zeit. | ||
| + | *Im Bereich $0 < t < T$ gilt deshalb: | ||
:$$h(t) = \frac{{\rm d}\hspace{0.1cm}\sigma(t)}{{\rm d}t}= 0.5 \cdot\left( \frac{1}{T} - 0.5 (\frac{2t}{T^2})\right) = \frac{0.5}{T} \cdot (1- \frac{t}{T})$$ | :$$h(t) = \frac{{\rm d}\hspace{0.1cm}\sigma(t)}{{\rm d}t}= 0.5 \cdot\left( \frac{1}{T} - 0.5 (\frac{2t}{T^2})\right) = \frac{0.5}{T} \cdot (1- \frac{t}{T})$$ | ||
:$$\Rightarrow \hspace{0.2cm} h(t = {\rm 1\, ms}) = h(t = T/2) = \frac{0.25}{T} \hspace{0.15cm}\underline{= 125 \cdot{1}/{ {\rm s} } },$$ | :$$\Rightarrow \hspace{0.2cm} h(t = {\rm 1\, ms}) = h(t = T/2) = \frac{0.25}{T} \hspace{0.15cm}\underline{= 125 \cdot{1}/{ {\rm s} } },$$ | ||
:$$\Rightarrow \hspace{0.2cm} h(t = {\rm 2\, ms}) = h(t = T) \hspace{0.15cm}\underline{= 0}.$$ | :$$\Rightarrow \hspace{0.2cm} h(t = {\rm 2\, ms}) = h(t = T) \hspace{0.15cm}\underline{= 0}.$$ | ||
| − | Für $t < 0$ und $t ≥ T$ | + | *Für $t < 0$ und $t ≥ T$ gilt stets $h(t)=0$. |
| + | *Der Wert $h(t = 0)$ bei exakt $t = 0$ muss aus dem Mittelwert zwischen links- und rechtsseitigem Grenzwert ermittelt werden: | ||
:$$h(t=0) = {1}/{2} \cdot \left[ \lim_{\varepsilon | :$$h(t=0) = {1}/{2} \cdot \left[ \lim_{\varepsilon | ||
\hspace{0.03cm} \to \hspace{0.03cm}0} h(- \varepsilon)+ \lim_{\varepsilon | \hspace{0.03cm} \to \hspace{0.03cm}0} h(- \varepsilon)+ \lim_{\varepsilon | ||
\hspace{0.03cm} \to \hspace{0.03cm} 0} h(+ \varepsilon)\right] = \left[ 0 + {0.5}/{T}\right] = {0.25}/{T}= 250 \cdot{1}/{ {\rm s} }.$$ | \hspace{0.03cm} \to \hspace{0.03cm} 0} h(+ \varepsilon)\right] = \left[ 0 + {0.5}/{T}\right] = {0.25}/{T}= 250 \cdot{1}/{ {\rm s} }.$$ | ||
| + | |||
[[Datei:P_ID829__LZI_A_1_3e.png | Berechnete Rechteckantwort| rechts|frame]] | [[Datei:P_ID829__LZI_A_1_3e.png | Berechnete Rechteckantwort| rechts|frame]] | ||
| − | '''(5)''' Der Rechteckimpuls $x_2(t)$ kann auch als die Differenz zweier um $±T/2$ verschobener Sprünge dargestellt werden: | + | '''(5)''' Der Rechteckimpuls $x_2(t)$ kann auch als die Differenz zweier um $±T/2$ verschobener Sprünge dargestellt werden: |
:$$x_2(t) = A \cdot \big[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big].$$ | :$$x_2(t) = A \cdot \big[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big].$$ | ||
| − | Damit ist das Ausgangssignal gleich der Differenz zweier um $±T/2$ verschobener Sprungantworten: | + | *Damit ist das Ausgangssignal gleich der Differenz zweier um $±T/2$ verschobener Sprungantworten: |
:$$y_2(t) = A \cdot \big[\sigma(t + {T}/{2}) - \sigma(t - {T}/{2})\big].$$ | :$$y_2(t) = A \cdot \big[\sigma(t + {T}/{2}) - \sigma(t - {T}/{2})\big].$$ | ||
| − | Für $t = \: -T/2 = -1\ \rm ms$ gilt $y_2(t) \;\underline{ = 0}$. | + | *Für $t = \: -T/2 = -1\ \rm ms$ gilt $y_2(t) \;\underline{ = 0}$. |
| − | Für die weiteren betrachteten Zeitpunkte erhält man wie in der Grafik angegeben: | + | *Für die weiteren betrachteten Zeitpunkte erhält man wie in der Grafik angegeben: |
:$$y_2(t = 0) = A \cdot \big[\sigma(0.5 \cdot T) - \sigma(-0.5 \cdot T)\big] = | :$$y_2(t = 0) = A \cdot \big[\sigma(0.5 \cdot T) - \sigma(-0.5 \cdot T)\big] = | ||
{\rm 2\, V}\cdot \left[0.1875 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.375\, V}},$$ | {\rm 2\, V}\cdot \left[0.1875 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.375\, V}},$$ | ||
Aktuelle Version vom 1. März 2021, 17:18 Uhr
An den Eingang eines linearen zeitinvarianten (LZI–)Übertragungssystems
- mit dem Frequenzgang $H(f)$
- und der Impulsantwort $h(t)$
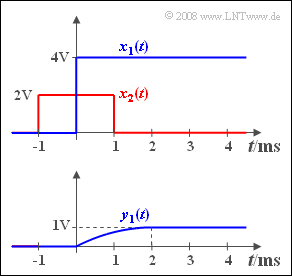
wird ein sprungförmiges Signal angelegt (blaue Kurve):
- $$x_1(t) = 4\hspace{0.05cm} {\rm V} \cdot \gamma(t).$$
Das gemessene Ausgangssignal $y_1(t)$ hat dann den unten dargestellten Verlauf.
- Mit $T = 2 \,{\rm ms}$ kann dieses Signal im Bereich von $0$ bis $T$ wie folgt beschrieben werden:
- $$y_1(t) = 2 \hspace{0.05cm}{\rm V} \cdot\big[ {t}/{T} - 0.5 \cdot ({t}/{T})^2\big].$$
- Ab $t = T $ ist $y_1(t)$ konstant gleich $1 \,{\rm V}$.
In der letzten Teilaufgabe (5) wird nach dem Ausgangssignal $y_2(t)$ gefragt, wenn am Eingang ein symmetrischer Rechteckimpuls $x_2(t)$ der Dauer $T = 2 \hspace{0.05cm} {\rm ms}$ anliegt (siehe roter Kurvenzug in der oberen Grafik).
Hinweise:
- Die Aufgabe gehört zum Kapitel Systembeschreibung im Zeitbereich
- Für den Rechteckimpuls $x_2(t)$ kann mit $A = 2 \hspace{0.05cm} \text{V}$ auch geschrieben werden:
- $$x_2(t) = A \cdot \big [\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big ].$$
- Der Frequenzgang $H(f)$ des hier betrachteten LZI–Systems kann dem Angabenblatt zu Aufgabe 3.8 im Buch „Signaldarstellung” entnommen werden. Allerdings sind die Abszissen– und Ordinatenparameter entsprechend anzupassen.
- Zur Lösung der vorliegenden Aufgabe wird $H(f)$ jedoch nicht explizit benötigt.
Fragebogen
Musterlösung
- Für das Ausgangssignal gilt $y_1(t)=0$, solange das Eingangssignal $x_1(t) = 0$ ist. Das bedeutet, dass hier ein kausales System vorliegt.
- Zum gleichen Ergebnis hätte man allein durch die Aussage „das Ausgangssignal wurde gemessen” kommen können. Nur kausale Systeme sind realisierbar und nur bei realisierbaren Systemen kann etwas gemessen werden.
- Das Eingangssignal $x_1(t)$ kann für sehr große Zeiten $(t \gg 0)$ als Gleichsignal interpretiert werden. Wäre $H(f)$ ein Hochpass, dann müsste $y_1(t)$ für $t → ∞$ gegen Null gehen. Das heißt: $H(f)$ stellt einen Tiefpass dar.
(2) Der Gleichsignalübertragungsfaktor kann aus $x_1(t)$ und $y_1(t)$ abgelesen werden, wenn der Einschwingvorgang abgeklungen ist:
- $$H(f =0) = \frac{y_1(t \rightarrow \infty)}{x_1(t \rightarrow \infty)}= \frac{ {\rm 1\, V} }{ {\rm 4\, V} } \hspace{0.15cm}\underline{= 0.25}.$$
(3) Die Sprungantwort $σ(t)$ ist gleich dem Ausgangssignal $y(t)$, wenn am Eingang $x(t) = γ(t)$ anliegen würde.
- Wegen $x_1(t) = 4 \hspace{0.05cm} \rm {V} · γ(t)$ gilt somit im Bereich von $0$ bis $T = 2 \ \rm ms$:
- $$\sigma(t) = \frac{y_1(t)}{ {\rm 4\, V} } = 0.5 \cdot\big( {t}/{T} - 0.5 ({t}/{T})^2\big).$$
- Zum Zeitpunkt $t = T = 2 \ \rm ms$ erreicht die Sprungantwort ihren Endwert $0.25$.
- Für $t = T/2 = 1 \ \rm ms$ ergibt sich der Zahlenwert $3/16 \; \underline{\: = \: 0.1875}$.
- Beachten Sie bitte, dass die Sprungantwort $σ(t)$ ebenso wie die Sprungfunktion $γ(t)$ keine Einheit besitzt.
(4) Die Sprungantwort $σ(t)$ ist das Integral über die Impulsantwort $h(t)$.
- Damit ergibt sich $h(t)$ aus $σ(t)$ durch Differentiation nach der Zeit.
- Im Bereich $0 < t < T$ gilt deshalb:
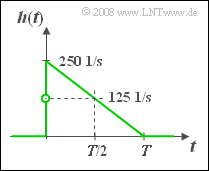
- $$h(t) = \frac{{\rm d}\hspace{0.1cm}\sigma(t)}{{\rm d}t}= 0.5 \cdot\left( \frac{1}{T} - 0.5 (\frac{2t}{T^2})\right) = \frac{0.5}{T} \cdot (1- \frac{t}{T})$$
- $$\Rightarrow \hspace{0.2cm} h(t = {\rm 1\, ms}) = h(t = T/2) = \frac{0.25}{T} \hspace{0.15cm}\underline{= 125 \cdot{1}/{ {\rm s} } },$$
- $$\Rightarrow \hspace{0.2cm} h(t = {\rm 2\, ms}) = h(t = T) \hspace{0.15cm}\underline{= 0}.$$
- Für $t < 0$ und $t ≥ T$ gilt stets $h(t)=0$.
- Der Wert $h(t = 0)$ bei exakt $t = 0$ muss aus dem Mittelwert zwischen links- und rechtsseitigem Grenzwert ermittelt werden:
- $$h(t=0) = {1}/{2} \cdot \left[ \lim_{\varepsilon \hspace{0.03cm} \to \hspace{0.03cm}0} h(- \varepsilon)+ \lim_{\varepsilon \hspace{0.03cm} \to \hspace{0.03cm} 0} h(+ \varepsilon)\right] = \left[ 0 + {0.5}/{T}\right] = {0.25}/{T}= 250 \cdot{1}/{ {\rm s} }.$$
(5) Der Rechteckimpuls $x_2(t)$ kann auch als die Differenz zweier um $±T/2$ verschobener Sprünge dargestellt werden:
- $$x_2(t) = A \cdot \big[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big].$$
- Damit ist das Ausgangssignal gleich der Differenz zweier um $±T/2$ verschobener Sprungantworten:
- $$y_2(t) = A \cdot \big[\sigma(t + {T}/{2}) - \sigma(t - {T}/{2})\big].$$
- Für $t = \: -T/2 = -1\ \rm ms$ gilt $y_2(t) \;\underline{ = 0}$.
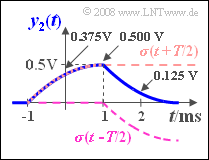
- Für die weiteren betrachteten Zeitpunkte erhält man wie in der Grafik angegeben:
- $$y_2(t = 0) = A \cdot \big[\sigma(0.5 \cdot T) - \sigma(-0.5 \cdot T)\big] = {\rm 2\, V}\cdot \left[0.1875 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.375\, V}},$$
- $$y_2(t = T/2) = y_2(t = 1\,{\rm ms}) =A \cdot \big[\sigma( T) - \sigma(0)\big] = {\rm 2\, V}\cdot \left[0.25 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.5\, V}},$$
- $$y_2(t = T) = A \cdot \big[\sigma(1.5 \cdot T) - \sigma(0.5 \cdot T)\big] = {\rm 2\, V}\cdot \big[0.25 - 0.1875\big] \hspace{0.15cm}\underline{= {\rm 0.125\, V}}.$$