Aufgaben:Aufgabe 3.2: Vom Spektrum zum Signal: Unterschied zwischen den Versionen
Aus LNTwww
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
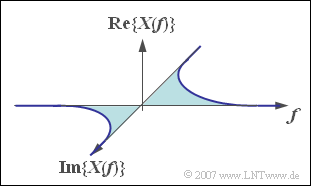
| − | [[Datei:P_ID495__Sig_A_3_2.png|right|Spektraldarstellung der Sprungfunktion | + | [[Datei:P_ID495__Sig_A_3_2.png|right|frame|Spektraldarstellung der Sprungfunktion]] |
Gegeben sei die Spektralfunktion | Gegeben sei die Spektralfunktion | ||
| − | $$X(f) = \frac{{2\,{\rm V}}}{ { {\rm j}\pi f}}.$$ | + | :$$X(f) = \frac{{2\,{\rm V}}}{ { {\rm j}\pi f}}.$$ |
| − | Die zugehörige Zeitfunktion $x(t)$ kann mit Hilfe des [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_zweite_Fourierintegral|zweiten Fourierintegrals]] ermittelt werden: | + | Die zugehörige Zeitfunktion $x(t)$ kann mit Hilfe des [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_zweite_Fourierintegral|zweiten Fourierintegrals]] ermittelt werden: |
| − | $$x(t) = \int_{ - \infty }^{ + \infty } {X(f)} \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d} f = x_{\rm R} (t) + {\rm j} \cdot x_{\rm I} (t),$$ | + | :$$x(t) = \int_{ - \infty }^{ + \infty } {X(f)} \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d} f = x_{\rm R} (t) + {\rm j} \cdot x_{\rm I} (t),$$ |
| − | wobei für den Realteil bzw. Imaginärteil gilt: | + | wobei für den Realteil bzw. den Imaginärteil gilt: |
| − | $$x_{\rm R} (t) = 2\,{\rm V} \cdot \int_{ - \infty }^{ + \infty } {\frac{{\sin ( {2\pi ft} )}}{ {\pi f}}}\hspace{0.1cm} {\rm d}f, | + | :$$x_{\rm R} (t) = 2\,{\rm V} \cdot \int_{ - \infty }^{ + \infty } {\frac{{\sin ( {2\pi ft} )}}{ {\pi f}}}\hspace{0.1cm} {\rm d}f, $$ |
| + | :$$x_{\rm I} (t) = -2\, {\rm V} \cdot \int_{ - \infty }^{ + \infty } {\frac{ {\cos ( {2\pi ft} )}}{ {\pi f}}} \hspace{0.1cm}{\rm d}f.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fouriertransformation_und_-rücktransformation|Fouriertransformation und | + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fouriertransformation_und_-rücktransformation|Fouriertransformation und –rücktransformation]]. |
| − | + | ||
*Benutzen Sie zur Lösung eventuell die nachfolgenden Angaben: | *Benutzen Sie zur Lösung eventuell die nachfolgenden Angaben: | ||
| − | :$$x( {t = 0}) = \int_{ - \infty }^{ + \infty } {X( f )}\hspace{0.1cm} {\rm d}f,\hspace{0.5cm} X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t)}\hspace{0. | + | :$$x( {t = 0}) = \int_{ - \infty }^{ + \infty } {X( f )}\hspace{0.1cm} {\rm d}f,\hspace{0.5cm} X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t)}\hspace{0.1cm} {\rm d}t ,\hspace{0.5cm}\int_0^\infty {\frac{{\sin ( {ax} )}}{x}}\hspace{0.1cm} {\rm d}x = {\rm sign} ( a ) \cdot{\pi }/{2}. $$ |
| Zeile 28: | Zeile 36: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche der folgenden Aussagen treffen für das Zeitsignal $x(t)$ zu? | + | {Welche der folgenden Aussagen treffen für das Zeitsignal $x(t)$ zu? |
| − | |type=" | + | |type="()"} |
| − | - $x(t)$ ist eine komplexe Funktion. | + | - $x(t)$ ist eine komplexe Funktion. |
| − | + $x(t)$ ist rein reell. | + | + $x(t)$ ist rein reell. |
| − | - $x(t)$ ist rein imaginär. | + | - $x(t)$ ist rein imaginär. |
| − | {Berechnen Sie den Signalverlauf $x(t)$ im gesamten Definitionsgebiet. Welche Werte treten zu den Zeiten $t = 1\, \text{ms}$ und $t = -\hspace{0. | + | {Berechnen Sie den Signalverlauf $x(t)$ im gesamten Definitionsgebiet. <br>Welche Werte treten zu den Zeiten $t = 1\, \text{ms}$ und $t = -\hspace{-0.05cm}1\, \text{ ms}$ auf? |
|type="{}"} | |type="{}"} | ||
| − | $x(t=+1\, \text{ms})$ | + | $x(t=+1\, \text{ms}) \ = \ $ { 2 3% } $\ \text{V}$ |
| − | $x(t=-1 \text{ms})$ | + | $x(t=-1 \text{ms})\hspace{0.2cm} = \ $ { -2.1--1.9 } $\ \text{V}$ |
| − | {Wie lautet der Signalwert zum Zeitpunkt $t = 0$? | + | {Wie lautet der Signalwert zum Zeitpunkt $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $x(t=0) | + | $x(t=0) \ = \ $ { 0. } $\ \text{V}$ |
{Wie groß ist der Spektralwert bei der Frequenz $f = 0$? | {Wie groß ist der Spektralwert bei der Frequenz $f = 0$? | ||
|type="{}"} | |type="{}"} | ||
| − | $X(f=0) | + | $X(f=0) \ = \ ${ 0. } $\ \text{V/Hz}$ |
</quiz> | </quiz> | ||
| Zeile 51: | Zeile 59: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u> ⇒ $x(t)$ ist <u>rein reell</u>: |
| + | *Beim imaginären Signalanteil ⇒ $x_{\rm I}(t)$ ist der Integrand eine ungerade Funktion (gerader Zähler, ungerader Nenner). | ||
| + | *Somit ist das Integral von $-\infty$ bis $+\infty$ gleich Null. | ||
| + | *Demgegenüber liefert beim reellen Anteil $x_{\rm R}(t)$ ⇒ gerader Integrand (ungerader Zähler, ungerader Nenner) einen von Null verschiedenen Wert. | ||
| − | |||
| − | '''2 | + | '''(2)''' Mit der Abkürzung $a = 2\pi t$ kann für das Zeitsignal geschrieben werden: |
| − | $$x(t) = x_{\rm R} \left( t \right) = \frac{{4\,{\rm V}}}{\pi }\int_0^\infty {\frac{{\sin( {af} )}}{f}}\hspace{0.1cm} {\rm d}f.$$ | + | :$$x(t) = x_{\rm R} \left( t \right) = \frac{{4\,{\rm V}}}{\pi }\int_0^\infty {\frac{{\sin( {af} )}}{f}}\hspace{0.1cm} {\rm d}f.$$ |
Dies führt unter Verwendung des angegebenen bestimmten Integrals zum Ergebnis: | Dies führt unter Verwendung des angegebenen bestimmten Integrals zum Ergebnis: | ||
| − | $$x(t) = \frac{{4\,{\rm V}}}{\pi } \cdot \frac{\pi }{2} \cdot {\mathop{\rm sign}\nolimits} ( t ) = 2\;{\rm V} \cdot {\mathop{\rm sign}\nolimits} ( t ).$$ | + | :$$x(t) = \frac{{4\,{\rm V}}}{\pi } \cdot \frac{\pi }{2} \cdot {\mathop{\rm sign}\nolimits} ( t ) = 2\;{\rm V} \cdot {\mathop{\rm sign}\nolimits} ( t ).$$ |
| − | Für $t > 0$ ist $x(t) = +2\,\text{V}$ . Entsprechend gilt $x(t) = -\hspace{-0.1cm}2\,\text{V}$ für $t < 0$. Das Signal $x(t)$ beschreibt also eine Sprungfunktion von $-\hspace{-0.05cm}2\,\text{V}$ auf $ | + | *Für $t > 0$ ist $x(t) = +2\,\text{V}$ . |
| + | *Entsprechend gilt $x(t) = -\hspace{-0.1cm}2\,\text{V}$ für $t < 0$. | ||
| + | *Das Signal $x(t)$ beschreibt also eine Sprungfunktion von $-\hspace{-0.05cm}2\,\text{V}$ auf $+2\,\text{V}$. | ||
| − | '''3 | + | |
| + | '''(3)''' Bei $t = 0$ besitzt $x(t)$ eine Sprungstelle. Der rechtsseitige Grenzwert für $t \rightarrow 0$ lautet $x_+ = +2\,\text{V}$. | ||
| + | *Nähert man sich der Sprungstelle von negativen Zeiten beliebig nahe, so erhält man $x_– = -\hspace{-0.05cm}2\,\text{V}$. Für den tatsächlichen Signalwert bei $t = 0$ gilt dann: | ||
| − | $$x( {t = 0} ) = {1}/{2}\cdot ( x_{+} + x_{-} ) \hspace{0.15 cm}\underline{= 0}.$$ | + | :$$x( {t = 0} ) = {1}/{2}\cdot ( x_{+} + x_{-} ) \hspace{0.15 cm}\underline{= 0}.$$ |
| + | |||
| + | *Zum gleichen Ergebnis kommt man bei Berücksichtigung der Beziehung | ||
| − | + | :$$x( t = 0) = \int_{ - \infty }^{ + \infty } {X( f)}\hspace{0.1cm} {\rm d}f = 0.$$ | |
| − | |||
| − | '''4 | + | '''(4)''' Der Spektralwert bei $f = 0$ ist gleich dem Integral von $-\infty$ bis $+\infty$ über die Zeitfunktion $x(t)$: |
| − | $$X( f = 0) = \int_{ - \infty }^{ + \infty } {x( t)}\hspace{0.1cm} {\rm d}t \hspace{0.15 cm}\underline{= 0}.$$ | + | :$$X( f = 0) = \int_{ - \infty }^{ + \infty } {x( t)}\hspace{0.1cm} {\rm d}t \hspace{0.15 cm}\underline{= 0}.$$ |
| − | Hier noch ein zweiter Lösungsweg: Der rechtsseitige Grenzwert für $f → 0$ ist $X_+ = | + | Hier noch ein zweiter Lösungsweg: |
| + | *Der rechtsseitige Grenzwert für $f → 0$ ist $X_+ = -\text{j} \cdot \infty$, der linksseitige Grenzwert $X_- = \text{j} \cdot \infty$. | ||
| + | *Auch bezüglich des Spektralwertes bei $f = 0$ gilt also der Zusammenhang: | ||
| − | $$X( {f = 0}) = {1}/{2}\cdot \left( {X_{ +} + X_{-} } \right) = 0.$$ | + | :$$X( {f = 0}) = {1}/{2}\cdot \left( {X_{ +} + X_{-} } \right) = 0.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 21. April 2021, 15:15 Uhr
Gegeben sei die Spektralfunktion
- $$X(f) = \frac{{2\,{\rm V}}}{ { {\rm j}\pi f}}.$$
Die zugehörige Zeitfunktion $x(t)$ kann mit Hilfe des zweiten Fourierintegrals ermittelt werden:
- $$x(t) = \int_{ - \infty }^{ + \infty } {X(f)} \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d} f = x_{\rm R} (t) + {\rm j} \cdot x_{\rm I} (t),$$
wobei für den Realteil bzw. den Imaginärteil gilt:
- $$x_{\rm R} (t) = 2\,{\rm V} \cdot \int_{ - \infty }^{ + \infty } {\frac{{\sin ( {2\pi ft} )}}{ {\pi f}}}\hspace{0.1cm} {\rm d}f, $$
- $$x_{\rm I} (t) = -2\, {\rm V} \cdot \int_{ - \infty }^{ + \infty } {\frac{ {\cos ( {2\pi ft} )}}{ {\pi f}}} \hspace{0.1cm}{\rm d}f.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Fouriertransformation und –rücktransformation.
- Benutzen Sie zur Lösung eventuell die nachfolgenden Angaben:
- $$x( {t = 0}) = \int_{ - \infty }^{ + \infty } {X( f )}\hspace{0.1cm} {\rm d}f,\hspace{0.5cm} X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t)}\hspace{0.1cm} {\rm d}t ,\hspace{0.5cm}\int_0^\infty {\frac{{\sin ( {ax} )}}{x}}\hspace{0.1cm} {\rm d}x = {\rm sign} ( a ) \cdot{\pi }/{2}. $$
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 2 ⇒ $x(t)$ ist rein reell:
- Beim imaginären Signalanteil ⇒ $x_{\rm I}(t)$ ist der Integrand eine ungerade Funktion (gerader Zähler, ungerader Nenner).
- Somit ist das Integral von $-\infty$ bis $+\infty$ gleich Null.
- Demgegenüber liefert beim reellen Anteil $x_{\rm R}(t)$ ⇒ gerader Integrand (ungerader Zähler, ungerader Nenner) einen von Null verschiedenen Wert.
(2) Mit der Abkürzung $a = 2\pi t$ kann für das Zeitsignal geschrieben werden:
- $$x(t) = x_{\rm R} \left( t \right) = \frac{{4\,{\rm V}}}{\pi }\int_0^\infty {\frac{{\sin( {af} )}}{f}}\hspace{0.1cm} {\rm d}f.$$
Dies führt unter Verwendung des angegebenen bestimmten Integrals zum Ergebnis:
- $$x(t) = \frac{{4\,{\rm V}}}{\pi } \cdot \frac{\pi }{2} \cdot {\mathop{\rm sign}\nolimits} ( t ) = 2\;{\rm V} \cdot {\mathop{\rm sign}\nolimits} ( t ).$$
- Für $t > 0$ ist $x(t) = +2\,\text{V}$ .
- Entsprechend gilt $x(t) = -\hspace{-0.1cm}2\,\text{V}$ für $t < 0$.
- Das Signal $x(t)$ beschreibt also eine Sprungfunktion von $-\hspace{-0.05cm}2\,\text{V}$ auf $+2\,\text{V}$.
(3) Bei $t = 0$ besitzt $x(t)$ eine Sprungstelle. Der rechtsseitige Grenzwert für $t \rightarrow 0$ lautet $x_+ = +2\,\text{V}$.
- Nähert man sich der Sprungstelle von negativen Zeiten beliebig nahe, so erhält man $x_– = -\hspace{-0.05cm}2\,\text{V}$. Für den tatsächlichen Signalwert bei $t = 0$ gilt dann:
- $$x( {t = 0} ) = {1}/{2}\cdot ( x_{+} + x_{-} ) \hspace{0.15 cm}\underline{= 0}.$$
- Zum gleichen Ergebnis kommt man bei Berücksichtigung der Beziehung
- $$x( t = 0) = \int_{ - \infty }^{ + \infty } {X( f)}\hspace{0.1cm} {\rm d}f = 0.$$
(4) Der Spektralwert bei $f = 0$ ist gleich dem Integral von $-\infty$ bis $+\infty$ über die Zeitfunktion $x(t)$:
- $$X( f = 0) = \int_{ - \infty }^{ + \infty } {x( t)}\hspace{0.1cm} {\rm d}t \hspace{0.15 cm}\underline{= 0}.$$
Hier noch ein zweiter Lösungsweg:
- Der rechtsseitige Grenzwert für $f → 0$ ist $X_+ = -\text{j} \cdot \infty$, der linksseitige Grenzwert $X_- = \text{j} \cdot \infty$.
- Auch bezüglich des Spektralwertes bei $f = 0$ gilt also der Zusammenhang:
- $$X( {f = 0}) = {1}/{2}\cdot \left( {X_{ +} + X_{-} } \right) = 0.$$