Aufgaben:Aufgabe 4.1: Tiefpass- und Bandpass-Signale: Unterschied zwischen den Versionen
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Signaldarstellung/ | + | {{quiz-Header|Buchseite=Signaldarstellung/Grundsätzliches_zu_Tiefpass-_und_Bandpass-Signalen |
}} | }} | ||
[[Datei:P_ID691__Sig_A_4_1.png|250px|right|frame|Vorgegebene Signalverläufe]] | [[Datei:P_ID691__Sig_A_4_1.png|250px|right|frame|Vorgegebene Signalverläufe]] | ||
| − | Rechts sind drei Signalverläufe skizziert, wobei die beiden ersten folgenden Verlauf aufweisen: | + | Rechts sind drei Signalverläufe skizziert, wobei die beiden ersten folgenden Verlauf aufweisen, mit ${\rm si}(x)=\sin(x)/x$: |
:$$x(t) = 10\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi \cdot | :$$x(t) = 10\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi \cdot | ||
| Zeile 13: | Zeile 13: | ||
{t}/{T_y}) .$$ | {t}/{T_y}) .$$ | ||
| − | $T_x = 100 \,{\rm µ}\text{s}$ und $T_y = 166.67 \,{\rm µ}\text{s}$ | + | Hierbei geben $T_x = 100 \,{\rm µ}\text{s}$ und $T_y = 166.67 \,{\rm µ}\text{s}$ jeweils die erste Nullstelle von $x(t)$ bzw. $y(t)$ an. |
| − | Das Signal $d(t)$ | + | Das Signal $d(t)$ ist die Differenz der beiden oberen Signale (untere Grafik): |
:$$d(t) = x(t)-y(t) .$$ | :$$d(t) = x(t)-y(t) .$$ | ||
| − | In der Teilaufgabe '''(4)''' ist nach den Integralflächen der | + | In der Teilaufgabe '''(4)''' ist nach den Integralflächen der zeitlich begrenzten Signale $x(t)$ und $d(t)$ gefragt. Für diese gilt: |
:$$F_x = \int_{- \infty}^{+\infty}\hspace{-0.4cm}x(t)\hspace{0.1cm}{\rm d}t , \hspace{0.5cm}F_d = \int_{- \infty}^{+\infty}\hspace{-0.4cm}d(t)\hspace{0.1cm}{\rm d}t .$$ | :$$F_x = \int_{- \infty}^{+\infty}\hspace{-0.4cm}x(t)\hspace{0.1cm}{\rm d}t , \hspace{0.5cm}F_d = \int_{- \infty}^{+\infty}\hspace{-0.4cm}d(t)\hspace{0.1cm}{\rm d}t .$$ | ||
| − | Dagegen gilt für die entsprechenden Signalenergien mit dem [[Signaldarstellung/Äquivalentes_Tiefpass-Signal_und_zugehörige_Spektralfunktion#Leistung_und_Energie_eines_Bandpass-Signals|Satz von Parseval]]: | + | Dagegen gilt für die entsprechenden Signalenergien mit dem [[Signaldarstellung/Äquivalentes_Tiefpass-Signal_und_zugehörige_Spektralfunktion#Leistung_und_Energie_eines_Bandpass-Signals|Satz von Parseval]]: |
:$$E_x = \int_{- \infty}^{+\infty}\hspace{-0.4cm}|x(t)|^2\hspace{0.1cm}{\rm | :$$E_x = \int_{- \infty}^{+\infty}\hspace{-0.4cm}|x(t)|^2\hspace{0.1cm}{\rm | ||
| Zeile 32: | Zeile 32: | ||
d}t = \int_{- \infty}^{+\infty}\hspace{-0.4cm}|D(f)|^2\hspace{0.1cm}{\rm | d}t = \int_{- \infty}^{+\infty}\hspace{-0.4cm}|D(f)|^2\hspace{0.1cm}{\rm | ||
d}f .$$ | d}f .$$ | ||
| + | |||
| + | |||
| + | |||
| Zeile 38: | Zeile 41: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/ | + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Grundsätzliches_zu_Tiefpass-_und_Bandpass-Signalen|Grundsätzliches zu Tiefpass- und Bandpass-Signalen]]. |
| − | *Die Fourierrücktransformierte eines rechteckförmigen Spektrums $X(f)$ führt zu einer $\rm si$–förmigen Zeitfunktion $x(t)$: | + | *Die Fourierrücktransformierte eines rechteckförmigen Spektrums $X(f)$ führt zu einer $\rm si$–förmigen Zeitfunktion $x(t)$: |
| − | :$$X(f)=\left\{ {X_0 \; \rm f\ddot{u}r\; |\it f| < \rm B, \atop {\rm 0 \;\;\; \rm sonst}}\right. \;\; | + | :$$X(f)=\left\{ {X_0 \; \rm f\ddot{u}r\; |\it \hspace{0.05cm}f\hspace{0.05cm}| < \rm B, \atop {\rm 0 \;\;\; \rm sonst}}\right. \;\; |
| − | \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \;\;x(t) = 2 \cdot X_0 \cdot B \cdot {\rm si} ( 2\pi B t) .$$ | + | \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \;\;x(t) = 2 \cdot X_0 \cdot B \cdot {\rm si} ( 2\pi B t), \hspace{0.5cm} {\rm si}(x)=\sin(x)/x.$$ |
| Zeile 49: | Zeile 52: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lautet das Spektrum $X(f)$ des Signals $x(t)$? Wie groß sind $X(f = 0)$ und die physikalische, einseitige Bandbreite $B_x$ von $x(t)$? | + | {Wie lautet das Spektrum $X(f)$ des Signals $x(t)$? Wie groß sind $X(f = 0)$ und die physikalische, einseitige Bandbreite $B_x$ von $x(t)$? |
|type="{}"} | |type="{}"} | ||
$X(f=0)\ = \ $ { 1 3% } $\text{mV/Hz}$ | $X(f=0)\ = \ $ { 1 3% } $\text{mV/Hz}$ | ||
$B_x \ = \ $ { 5 3% } $\text{kHz}$ | $B_x \ = \ $ { 5 3% } $\text{kHz}$ | ||
| − | {Wie lauten die entsprechenden Kenngrößen des Signals $y(t)$? | + | {Wie lauten die entsprechenden Kenngrößen des Signals $y(t)$? |
|type="{}"} | |type="{}"} | ||
$Y(f=0)\ = \ $ { 1 3% } $\text{mV/Hz}$ | $Y(f=0)\ = \ $ { 1 3% } $\text{mV/Hz}$ | ||
| Zeile 60: | Zeile 63: | ||
| − | {Berechnen Sie das Spektrum $D(f)$ des Differenzsignals $d(t) = x(t) - y(t)$. Wie groß sind $D(f = 0)$ und die (einseitige) Bandbreite $B_d$? | + | {Berechnen Sie das Spektrum $D(f)$ des Differenzsignals $d(t) = x(t) - y(t)$. Wie groß sind $D(f = 0)$ und die (einseitige) Bandbreite $B_d$? |
|type="{}"} | |type="{}"} | ||
$D(f=0)\ = \ $ { 0. } $\text{mV/Hz}$ | $D(f=0)\ = \ $ { 0. } $\text{mV/Hz}$ | ||
$B_d \ = \ $ { 2 3% } $\text{kHz}$ | $B_d \ = \ $ { 2 3% } $\text{kHz}$ | ||
| − | {Wie groß sind die Integralflächen $F_x$ und $F_d$ der Signale $x(t)$ und $d(t)$? | + | {Wie groß sind die Integralflächen $F_x$ und $F_d$ der Signale $x(t)$ und $d(t)$? |
|type="{}"} | |type="{}"} | ||
$F_x\ = \ $ { 0.001 } $\text{Vs}$ | $F_x\ = \ $ { 0.001 } $\text{Vs}$ | ||
$F_d\ = \ $ { 0. } $\text{Vs}$ | $F_d\ = \ $ { 0. } $\text{Vs}$ | ||
| − | {Wie groß sind die (auf $1\ Ω$ umgerechneten) Energien dieser Signale? | + | {Wie groß sind die (auf $1\ Ω$ umgerechneten) Energien dieser Signale? |
|type="{}"} | |type="{}"} | ||
$E_x \ = \ $ { 0.01 3% } $\text{V}^2\text{s}$ | $E_x \ = \ $ { 0.01 3% } $\text{V}^2\text{s}$ | ||
| Zeile 80: | Zeile 83: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die | + | '''(1)''' Die $\rm si$–förmige Zeitfunktion $x(t)$ lässt auf ein Rechteckspektrum $X(f)$ schließen. |
| + | *Die absolute, zweiseitige Bandbreite $2 \cdot B_x$ ist gleich dem Kehrwert der ersten Nullstelle. Daraus folgt: | ||
:$$B_x = \frac{1}{2 \cdot T_x} = \frac{1}{2 \cdot 0.1 | :$$B_x = \frac{1}{2 \cdot T_x} = \frac{1}{2 \cdot 0.1 | ||
\hspace{0.1cm}{\rm ms}}\hspace{0.15 cm}\underline{ = 5 \hspace{0.1cm}{\rm kHz}}.$$ | \hspace{0.1cm}{\rm ms}}\hspace{0.15 cm}\underline{ = 5 \hspace{0.1cm}{\rm kHz}}.$$ | ||
| − | Da der Signalwert bei $t = 0$ gleich der Rechteckfläche ist, ergibt sich für die konstante Höhe: | + | *Da der Signalwert bei $t = 0$ gleich der Rechteckfläche ist, ergibt sich für die konstante Höhe: |
:$$X(f=0) = \frac{x(t=0)}{2 B_x} = \frac{10 | :$$X(f=0) = \frac{x(t=0)}{2 B_x} = \frac{10 | ||
| Zeile 92: | Zeile 96: | ||
| − | |||
| + | '''(2)''' Aus $T_y = 0.167 \,\text{ms}$ erhält man $B_y \;\underline{= 3 \,\text{kHz}}$. | ||
| + | *Zusammen mit $y(t = 0) = 6\,\text{V}$ führt dies zum gleichen Spektralwert $Y(f = 0)\; \underline{= 1\, \text{mV/Hz}}$ wie bei der Teilaufgabe '''(1)'''. | ||
| − | |||
| − | |||
| − | |||
| − | |||
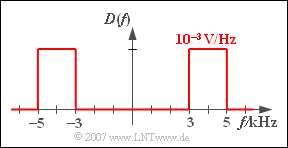
| − | '''(4)''' Nach den fundamentalen Gesetzmäßigkeiten der Fouriertransformation ist das Integral über die Zeitfunktion gleich dem Spektralwert bei $f = 0$. Daraus folgt: | + | [[Datei:P_ID701__Sig_A_4_1_c_neu.png|right|frame|Rechteckförmiges Bandpass–Spektrum]] |
| + | '''(3)''' Aus $d(t) = x(t) - y(t)$ folgt wegen der Linearität der Fouriertransformation: $D(f) = X(f) - Y(f).$ | ||
| + | |||
| + | *Die Differenz der zwei gleich hohen Rechteckfunktionen führt zu einem rechteckförmigen Bandpass–Spektrum zwischen $3 \,\text{kHz}$ und $5 \,\text{kHz}$. | ||
| + | *Die (einseitige) Bandbreite beträgt somit $B_d \;\underline{= 2 \,\text{kHz}}$. In diesem Frequenzintervall ist $D(f) = 1 \,\text{mV/Hz}$. Außerhalb, also auch bei $f = 0$, gilt $D(f)\;\underline{ = 0}$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Nach den fundamentalen Gesetzmäßigkeiten der Fouriertransformation ist das Integral über die Zeitfunktion gleich dem Spektralwert bei $f = 0$. Daraus folgt: | ||
:$$F_x = X(f=0) = \frac{x(t=0)}{2 \cdot B_x} = 10^{-3} | :$$F_x = X(f=0) = \frac{x(t=0)}{2 \cdot B_x} = 10^{-3} | ||
| Zeile 109: | Zeile 119: | ||
:$$F_d = D(f=0) \hspace{0.15 cm}\underline{= 0}.$$ | :$$F_d = D(f=0) \hspace{0.15 cm}\underline{= 0}.$$ | ||
| − | ⇒ Bei jedem Bandpass–Signal sind die Flächen der positiven Signalanteile gleich groß wie die Flächen der negativen Anteile. | + | ⇒ '''Bei jedem Bandpass–Signal sind die Flächen der positiven Signalanteile gleich groß wie die Flächen der negativen Anteile'''. |
| + | |||
Aktuelle Version vom 3. Mai 2021, 17:08 Uhr
Rechts sind drei Signalverläufe skizziert, wobei die beiden ersten folgenden Verlauf aufweisen, mit ${\rm si}(x)=\sin(x)/x$:
- $$x(t) = 10\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi \cdot {t}/{T_x}) ,$$
- $$y(t) = 6\hspace{0.05cm}{\rm V} \cdot {\rm si}( \pi \cdot {t}/{T_y}) .$$
Hierbei geben $T_x = 100 \,{\rm µ}\text{s}$ und $T_y = 166.67 \,{\rm µ}\text{s}$ jeweils die erste Nullstelle von $x(t)$ bzw. $y(t)$ an.
Das Signal $d(t)$ ist die Differenz der beiden oberen Signale (untere Grafik):
- $$d(t) = x(t)-y(t) .$$
In der Teilaufgabe (4) ist nach den Integralflächen der zeitlich begrenzten Signale $x(t)$ und $d(t)$ gefragt. Für diese gilt:
- $$F_x = \int_{- \infty}^{+\infty}\hspace{-0.4cm}x(t)\hspace{0.1cm}{\rm d}t , \hspace{0.5cm}F_d = \int_{- \infty}^{+\infty}\hspace{-0.4cm}d(t)\hspace{0.1cm}{\rm d}t .$$
Dagegen gilt für die entsprechenden Signalenergien mit dem Satz von Parseval:
- $$E_x = \int_{- \infty}^{+\infty}\hspace{-0.4cm}|x(t)|^2\hspace{0.1cm}{\rm d}t = \int_{- \infty}^{+\infty}\hspace{-0.4cm}|X(f)|^2\hspace{0.1cm}{\rm d}f ,$$
- $$E_d = \int_{- \infty}^{+\infty}\hspace{-0.4cm}|d(t)|^2\hspace{0.1cm}{\rm d}t = \int_{- \infty}^{+\infty}\hspace{-0.4cm}|D(f)|^2\hspace{0.1cm}{\rm d}f .$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Grundsätzliches zu Tiefpass- und Bandpass-Signalen.
- Die Fourierrücktransformierte eines rechteckförmigen Spektrums $X(f)$ führt zu einer $\rm si$–förmigen Zeitfunktion $x(t)$:
- $$X(f)=\left\{ {X_0 \; \rm f\ddot{u}r\; |\it \hspace{0.05cm}f\hspace{0.05cm}| < \rm B, \atop {\rm 0 \;\;\; \rm sonst}}\right. \;\; \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \;\;x(t) = 2 \cdot X_0 \cdot B \cdot {\rm si} ( 2\pi B t), \hspace{0.5cm} {\rm si}(x)=\sin(x)/x.$$
Fragebogen
Musterlösung
- Die absolute, zweiseitige Bandbreite $2 \cdot B_x$ ist gleich dem Kehrwert der ersten Nullstelle. Daraus folgt:
- $$B_x = \frac{1}{2 \cdot T_x} = \frac{1}{2 \cdot 0.1 \hspace{0.1cm}{\rm ms}}\hspace{0.15 cm}\underline{ = 5 \hspace{0.1cm}{\rm kHz}}.$$
- Da der Signalwert bei $t = 0$ gleich der Rechteckfläche ist, ergibt sich für die konstante Höhe:
- $$X(f=0) = \frac{x(t=0)}{2 B_x} = \frac{10 \hspace{0.1cm}{\rm V}}{10 \hspace{0.1cm}{\rm kHz}} \hspace{0.15 cm}\underline{= 1 \hspace{0.1cm}{\rm mV/Hz}}.$$
(2) Aus $T_y = 0.167 \,\text{ms}$ erhält man $B_y \;\underline{= 3 \,\text{kHz}}$.
- Zusammen mit $y(t = 0) = 6\,\text{V}$ führt dies zum gleichen Spektralwert $Y(f = 0)\; \underline{= 1\, \text{mV/Hz}}$ wie bei der Teilaufgabe (1).
(3) Aus $d(t) = x(t) - y(t)$ folgt wegen der Linearität der Fouriertransformation: $D(f) = X(f) - Y(f).$
- Die Differenz der zwei gleich hohen Rechteckfunktionen führt zu einem rechteckförmigen Bandpass–Spektrum zwischen $3 \,\text{kHz}$ und $5 \,\text{kHz}$.
- Die (einseitige) Bandbreite beträgt somit $B_d \;\underline{= 2 \,\text{kHz}}$. In diesem Frequenzintervall ist $D(f) = 1 \,\text{mV/Hz}$. Außerhalb, also auch bei $f = 0$, gilt $D(f)\;\underline{ = 0}$.
(4) Nach den fundamentalen Gesetzmäßigkeiten der Fouriertransformation ist das Integral über die Zeitfunktion gleich dem Spektralwert bei $f = 0$. Daraus folgt:
- $$F_x = X(f=0) = \frac{x(t=0)}{2 \cdot B_x} = 10^{-3} \hspace{0.1cm}{\rm V/Hz}\hspace{0.15 cm}\underline{= 0.001 \hspace{0.1cm}{\rm Vs}},$$
- $$F_d = D(f=0) \hspace{0.15 cm}\underline{= 0}.$$
⇒ Bei jedem Bandpass–Signal sind die Flächen der positiven Signalanteile gleich groß wie die Flächen der negativen Anteile.
(5) In beiden Fällen ist die Berechnung der Signalenergie im Frequenzbereich einfacher als im Zeitbereich, da hier die Integration auf eine Flächenberechnung von Rechtecken zurückgeführt werden kann:
- $$E_x = (10^{-3} \hspace{0.1cm}{\rm V/Hz})^2 \cdot 2 \cdot 5 \hspace{0.1cm}{\rm kHz} \hspace{0.15 cm}\underline{= 0.01 \hspace{0.1cm}{\rm V^2s}},$$
- $$E_d = (10^{-3} \hspace{0.1cm}{\rm V/Hz})^2 \cdot 2 \cdot 2 \hspace{0.1cm}{\rm kHz} \hspace{0.15 cm}\underline{= 0.004 \hspace{0.1cm}{\rm V^2s}}.$$