Signaldarstellung/Fast-Fouriertransformation (FFT): Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
==Rechenaufwand von DFT bzw. IDFT== | ==Rechenaufwand von DFT bzw. IDFT== | ||
| − | + | <br> | |
| − | Ein Nachteil der direkten Berechnung der (im Allgemeinen komplexen) DFT–Zahlenfolgen | + | Ein Nachteil der direkten Berechnung der (im Allgemeinen komplexen) DFT–Zahlenfolgen |
| − | :$$\langle D(\mu)\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle d(\nu) \rangle$$ | + | :$$\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d(\nu)\hspace{0.1cm} \rangle$$ |
| − | gemäß den in Kapitel [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskrete Fouriertransformation | + | gemäß den in Kapitel [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskrete Fouriertransformation]] angegebenen Gleichungen ist der große Rechenaufwand. Wir betrachten als Beispiel die $\rm DFT$, also die Berechnung der Spektralkoeffizienten $D(\mu)$ aus den Zeitkoeffizienten $d(\nu)$: |
:$$N \cdot D(\mu) = \sum_{\nu = 0 }^{N-1} | :$$N \cdot D(\mu) = \sum_{\nu = 0 }^{N-1} | ||
d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} | d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} | ||
= | = | ||
| − | d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+\hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}$$ | + | d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+\hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}.$$ |
| − | Der hierfür erforderliche Rechenaufwand soll | + | Der hierfür erforderliche Rechenaufwand soll abgeschätzt werden, wobei wir davon ausgehen, dass die Potenzen des komplexen Drehfaktors $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N}$ bereits in Real– und Imaginärteilform in einer Lookup–Tabelle vorliegen. |
| + | |||
| + | Zur Berechnung eines einzelnen Koeffizienten benötigt man dann $N-1$ komplexe Multiplikationen und ebenso viele komplexe Additionen, wobei zu beachten ist: | ||
*Jede komplexe Addition erfordert zwei reelle Additionen: | *Jede komplexe Addition erfordert zwei reelle Additionen: | ||
:$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + | :$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + | ||
| Zeile 27: | Zeile 29: | ||
R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot | R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot | ||
I_1)\hspace{0.05cm}.$$ | I_1)\hspace{0.05cm}.$$ | ||
| − | *Somit sind zur Berechnung aller $N$ Koeffizienten insgesamt die folgende Anzahl $M$ reeller Multiplikationen und die Anzahl $A$ reeller Additionen erforderlich: | + | *Somit sind zur Berechnung aller $N$ Koeffizienten insgesamt die folgende Anzahl $M$ reeller Multiplikationen und die Anzahl $A$ reeller Additionen erforderlich: |
:$$M = 4 \cdot N \cdot (N-1),$$ | :$$M = 4 \cdot N \cdot (N-1),$$ | ||
:$$A = 2 \cdot N \cdot | :$$A = 2 \cdot N \cdot | ||
(N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$ | (N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$ | ||
| − | *In heutigen Rechnern benötigen Multiplikationen und Additionen/Subtraktionen etwa die gleiche Rechenzeit. Es genügt, die Gesamtzahl $\mathcal{O} = M + A$ aller Operationen zu betrachten: | + | *In heutigen Rechnern benötigen Multiplikationen und Additionen/Subtraktionen etwa die gleiche Rechenzeit. Es genügt, die Gesamtzahl $\mathcal{O} = M + A$ aller Operationen zu betrachten: |
:$$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$ | :$$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Fazit:}$ | + | $\text{Fazit:}$ |
| + | *Man benötigt bereits für eine Diskrete Fouriertransformation $\rm (DFT)$ mit $N = 1000$ knapp acht Millionen Rechenoperationen. Gleiches gilt für eine $\rm IDFT$. | ||
| + | *Mit $N =16 $ sind immerhin noch $1920$ Rechenoperationen erforderlich.}} | ||
| − | Ist der Parameter $N$ eine Potenz zur Basis $2$, so können rechenzeitgünstigere Algorithmen angewendet werden. Die Vielzahl solcher aus der Literatur bekannten Verfahren werden unter dem | + | |
| + | Ist der Parameter $N$ eine Potenz zur Basis $2$, so können rechenzeitgünstigere Algorithmen angewendet werden. Die Vielzahl solcher aus der Literatur bekannten Verfahren werden unter dem Begriff $\text{Fast–Fouriertransformation}$ – abgekürzt $\text{FFT}$ – zusammengefasst. Alle diese Methoden basieren auf dem Überlagerungssatz der DFT. | ||
==Überlagerungssatz der DFT== | ==Überlagerungssatz der DFT== | ||
| + | <br> | ||
| + | Die Grafik verdeutlicht den so genannten Überlagerungssatz der DFT am Beispiel $N = 16$. Dargestellt ist hier der Übergang vom Zeit– in den Spektralbereich, also die Berechnung der Spektralbereichskoeffizienten aus den Zeitbereichskoeffizienten: $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle.$ | ||
| − | + | [[Datei:P_ID1170__Sig_T_5_5_S2_v2.png|right|frame|Überlagerungssatz der DFT]] | |
| − | |||
| − | [[Datei:P_ID1170__Sig_T_5_5_S2_v2.png| | ||
Der dadurch beschriebene Algorithmus ist durch folgende Schritte gekennzeichnet: | Der dadurch beschriebene Algorithmus ist durch folgende Schritte gekennzeichnet: | ||
| − | *Die Folge $\langle d(\nu)\rangle$ der Länge $N$ wird in zwei Teilfolgen $\langle d_1(\nu)\rangle$ und $\langle d_2(\nu)\rangle$ jeweils halber Länge separiert (in der Garafik gelb bzw. grün hinterlegt). Mit $0 \le \nu \lt N/2$ erhält man so die Folgenelemente | + | *Die Folge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ der Länge $N$ wird in zwei Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} d_2(\nu)\hspace{0.1cm}\rangle$ jeweils halber Länge separiert (in der Garafik gelb bzw. grün hinterlegt). Mit $0 \le \nu \lt N/2$ erhält man so die Folgenelemente |
:$$d_1(\nu) = d(2\nu), $$ | :$$d_1(\nu) = d(2\nu), $$ | ||
:$$d_2(\nu) = d(2\nu+1) | :$$d_2(\nu) = d(2\nu+1) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Die Ausgangsfolgen $\langle D_1(\mu )\rangle$ und $\langle D_2(\mu )\rangle$ der beiden Teilblöcke ergeben sich daraus jeweils durch eine eigene DFT, aber nun nur noch mit halber Länge $N/2 = 8$: | + | *Die Ausgangsfolgen $\langle \hspace{0.1cm}D_1(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}D_2(\mu )\hspace{0.1cm}\rangle$ der beiden Teilblöcke ergeben sich daraus jeweils durch eine eigene DFT, aber nun nur noch mit halber Länge $N/2 = 8$: |
| − | :$$\langle D_1(\mu) \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle d_1(\nu) \rangle , $$ | + | :$$\langle \hspace{0.1cm}D_1(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_1(\nu) \hspace{0.1cm}\rangle , $$ |
| − | :$$ \langle D_2(\mu) \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle d_2(\nu) \rangle \hspace{0.05cm}.$$ | + | :$$ \langle \hspace{0.1cm}D_2(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_2(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$ |
| − | *Die Ausgangswerte $\langle D_2(\mu )\rangle$ der unteren | + | *Die Ausgangswerte $\langle \hspace{0.1cm} D_2(\mu )\hspace{0.1cm}\rangle$ der unteren, grünen DFT $($mit $0 \le \mu \lt N/2)$ werden danach im rot umrandeten Block durch komplexe Drehfaktoren hinsichtlich der Phasenlage verändert: |
:$$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm wobei}\hspace{0.1cm}w = | :$$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm wobei}\hspace{0.1cm}w = | ||
{\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$ | {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$ | ||
| − | *Jeder einzelne | + | *Jeder einzelne $\text{Butterfly}$ im blau umrandeten Block (in der Grafikmitte) liefert durch Addition bzw. Subtraktion zwei Elemente der gesuchten Ausgangsfolge. Mit $0 \le \mu \lt N/2$ gilt dabei: |
| − | :$$D(\mu) = {1}/{2}\cdot \ | + | :$$D(\mu) = {1}/{2}\cdot \big[D_1(\mu) + D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big],$$ |
| − | :$$D(\mu +{N}/{2}) = {1}/{2}\cdot \ | + | :$$D(\mu +{N}/{2}) = {1}/{2}\cdot \big[D_1(\mu) - D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big]\hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | |||
| + | '''Durch diese erste Anwendung des Überlagerungssatzes halbiert sich somit in etwa der Rechenaufwand'''. | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ | $\text{Beispiel 1:}$ | ||
| − | Die DFT–Koeffizienten $d(\nu)$ zur Beschreibung des Zeitverlaufs seien entsprechend der Zeile 2 der folgenden Tabelle „dreieckförmig” belegt. Beachten Sie hierbei die periodische Fortsetzung der DFT, so dass der lineare Anstieg für $t \lt 0$ durch die Koeffizienten $d(8) \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, d(15)$ ausgedrückt wird. | + | Die DFT–Koeffizienten $d(\nu)$ zur Beschreibung des Zeitverlaufs seien entsprechend der '''Zeile 2''' der folgenden Tabelle „dreieckförmig” belegt. Beachten Sie hierbei die periodische Fortsetzung der DFT, so dass der lineare Anstieg für $t \lt 0$ durch die Koeffizienten $d(8), \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, d(15)$ ausgedrückt wird. |
| − | Durch Anwendung des DFT–Algorithmus mit $N = 16$ erhält man die in der Zeile 3 angegebenen Spektralkoeffizienten $D(\mu )$, die bei Vernachlässigung des Aliasingfehlers gleich $D(\mu ) = 4 \cdot \text{si}^2(\pi \cdot \mu/2)$ wären. Man erkennt, dass sich der Aliasingfehler nur auf die ungeradzahligen Koeffizienten auswirkt (schraffierte Felder). Beispielsweise müsste $D | + | Durch Anwendung des DFT–Algorithmus mit $N = 16$ erhält man die in der '''Zeile 3''' angegebenen Spektralkoeffizienten $D(\mu )$, die bei Vernachlässigung des Aliasingfehlers gleich $D(\mu ) = 4 \cdot \text{si}^2(\pi \cdot \mu/2)$ wären. Man erkennt, dass sich der Aliasingfehler nur auf die ungeradzahligen Koeffizienten auswirkt (schraffierte Felder). Beispielsweise müsste $D(1) = 16/ \pi^2 \approx 1.621\neq 1.642$ sein. |
| − | [[Datei:Sig_T_5_5_S2b_Version2.png| | + | [[Datei:Sig_T_5_5_S2b_Version2.png|right|frame|Ergebnistabelle zum $\text{Beispiel 1}$ zum Überlagerungssatz der DFT]] |
| − | Spaltet man die Gesamtfolge $\langle d(\nu)\rangle$ in zwei Teilfolgen $\langle {d_1}'(\nu)\rangle$ und $\langle {d_2}'(\nu)\rangle$ auf, und zwar derart, dass die erste (gelb hinterlegte) Teilfolge nur geradzahlige Koeffizienten ( | + | Spaltet man die Gesamtfolge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ in zwei Teilfolgen $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {d_2}'(\nu)\hspace{0.1cm}\rangle$ auf, und zwar derart, dass die erste (gelb hinterlegte) Teilfolge nur geradzahlige Koeffizienten $(\nu = 0,\ 2, \hspace{0.03cm}\text{ ...} \hspace{0.1cm},\ N–2)$ und die zweite (grün hinterlegt) nur ungeradzahlige Koeffizienten $(\nu = 1,\ 3,\ \hspace{0.03cm}\text{ ...} \hspace{0.1cm} ,\ N–1)$ beinhalten und alle anderen zu Null gesetzt sind, so erhält man die zugehörigen Folgen im Spektralbereich: |
| − | :$$ \langle {D_1}'(\mu) \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle {d_1}'(\nu) \rangle , $$ | + | :$$ \langle \hspace{0.1cm}{D_1}'(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} {d_1}'(\nu) \hspace{0.1cm}\rangle , $$ |
| − | :$$ \langle {D_2}'(\mu) \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle {d_2}'(\nu) \rangle \hspace{0.05cm}.$$ | + | :$$ \langle \hspace{0.1cm}{D_2}'(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle\hspace{0.1cm} {d_2}'(\nu) \rangle \hspace{0.1cm}\hspace{0.05cm}.$$ |
| − | In den gelb bzw. grün hinterlegten Zeilen $4\hspace{0.05cm}\text{ ...} \hspace{0.05cm}7$ erkennt man: | + | In den gelb bzw. grün hinterlegten Zeilen $4\hspace{0.05cm}\text{ ...} \hspace{0.05cm}7$ erkennt man: |
| − | *Wegen $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$ gilt auch $D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu )$ | + | *Wegen $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$ gilt auch: |
| − | *Die Periode der Folge $\langle {D_1}'(\mu )\rangle$ | + | :$$D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu ).$$ |
| + | :Dies lässt sich zum Beispiel mit dem [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Multiplikation_mit_Faktor_-_Additionssatz|Additionstheorem linearer Systeme]] begründen. | ||
| + | *Die Periode der Folge $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ ist aufgrund des Nullsetzens eines jeden zweiten Zeitkoeffizienten nun $N/2$ im Gegensatz zur Periode $N$ der Folge $\langle \hspace{0.1cm} D(\mu )\hspace{0.1cm}\rangle$: | ||
:$${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$ | :$${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$ | ||
| − | * $\langle {D_2}'(\mu )\rangle$ beinhaltet zusätzlich einen Phasenfaktor (Verschiebung um einen Abtastwert), der einen Vorzeichenwechsel zweier um $N/2$ auseinanderliegender Koeffizienten bewirkt: | + | *Die Folge $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ beinhaltet zusätzlich einen Phasenfaktor (aufgrund der Verschiebung um einen Abtastwert), der einen Vorzeichenwechsel zweier um $N/2$ auseinanderliegender Koeffizienten bewirkt: |
| − | :$${D_2}'(\mu + {N}/{2}) =-{D_2}'(\mu)\hspace{0.05cm}.$$ | + | :$${D_2}'(\mu + {N}/{2}) = - {D_2}'(\mu)\hspace{0.05cm}.$$ |
| − | *Die Berechnung von $\langle {D_1}'(\mu )\rangle$ und $\langle {D_2}'(\mu )\rangle$ ist | + | *Die Berechnung von $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ ist allerdings ebenso aufwändig wie die Bestimmung von $\langle \hspace{0.1cm}D(\mu )\hspace{0.1cm}\rangle$, da $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}'(\nu)\hspace{0.1cm}\rangle$ ebenfalls aus $N$ Elementen bestehen, auch wenn die Hälfte davon Nullen sind.}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 2:}$ | $\text{Beispiel 2:}$ | ||
| − | Zur Fortsetzung des ersten Beispiels wird nun die bisherige Tabelle um die Zeilen 8 bis 12 erweitert. | + | Zur Fortsetzung des ersten Beispiels wird nun die bisherige Tabelle um die Zeilen $8$ bis $12$ erweitert. |
| − | [[Datei:Sig_T_5_5_S2c_Version2.png| | + | [[Datei:Sig_T_5_5_S2c_Version2.png|right|frame|Ergebnistabelle zum $\text{Beispiel 2}$ zum Überlagerungssatz der DFT]] |
| − | Verzichtet man auf die Koeffizienten ${d_1}'(\nu) = 0$ mit ungeraden sowie auf ${d_2}'(\nu) = 0$ mit geraden Indizes, so kommt man zu den Teilfolgen $\langle d_1(\nu)\rangle$ und $\langle d_2(\nu)\rangle$ entsprechend den Zeilen 9 und 11. Man erkennt: | + | Verzichtet man auf die Koeffizienten ${d_1}'(\nu) = 0$ mit ungeraden sowie auf ${d_2}'(\nu) = 0$ mit geraden Indizes, so kommt man zu den Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}d_2(\nu)\hspace{0.1cm}\rangle$ entsprechend den Zeilen $9$ und $11$ . Man erkennt: |
| − | *Die | + | *Die Zeitfolgen $\langle \hspace{0.1cm}{d_1}(\nu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}(\nu )\hspace{0.1cm}\rangle$ weisen ebenso wie die dazugehörigen Spektralfolgen $\langle \hspace{0.1cm}{D_1}(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{D_2}(\mu )\hspace{0.1cm}\rangle$ nur noch die Dimension $N/2$ auf. |
| − | *Ein Vergleich der Zeilen 5, 7, 10 und 12 zeigt für $0 \le \mu \lt N/2$ folgenden Zusammenhang: | + | *Ein Vergleich der Zeilen $5$, $7$, $10$ und $12$ zeigt für $0 \le \mu \lt N/2$ folgenden Zusammenhang: |
:$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu)\hspace{0.05cm},$$ | :$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu)\hspace{0.05cm},$$ | ||
:$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu)\cdot w^{\hspace{0.04cm}\mu}\hspace{0.05cm}.$$ | :$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu)\cdot w^{\hspace{0.04cm}\mu}\hspace{0.05cm}.$$ | ||
| − | *Entsprechend | + | *Entsprechend ergibt sich für $N/2 \le \mu \lt N$: |
| − | :$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu-{N}/{2})\hspace{0.05cm},$$ | + | :$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu - {N}/{2})\hspace{0.05cm},$$ |
| − | :$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu-{N}/{2})\cdot w^{\hspace{0.04cm}\mu} | + | :$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu {-} {N}/{2})\cdot w^{\hspace{0.04cm}\mu}$$ |
| − | + | :$$ \Rightarrow \hspace{0.3cm}{D_2}'(\mu) = { - } {1}/{2}\cdot {D_2}(\mu-N/2)\cdot w^{\hspace{0.04cm}\mu {-} N/2}\hspace{0.05cm}. | |
| − | *Zum Beispiel erhält man mit $N = 16$ ⇒ $w = {\rm e}^{–{\rm j}\hspace{0.04cm} \cdot \hspace{0.04cm}\pi/8}$ für die Indizes $\mu = 1$ bzw. $\mu = 9$: | + | $$ |
| + | |||
| + | *Zum Beispiel erhält man mit $N = 16$ ⇒ $w = {\rm e}^{ – {\rm j}\hspace{0.04cm} \cdot \hspace{0.04cm}\pi/8}$ für die Indizes $\mu = 1$ bzw. $\mu = 9$: | ||
:$${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} | :$${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} | ||
| − | {D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} | + | {D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} |
\pi/8} = 0.788$$ | \pi/8} = 0.788$$ | ||
:$$\Rightarrow D(1) = {D_1}'(1)+ {D_2}'(1)= 1.642 \hspace{0.05cm}.$$ | :$$\Rightarrow D(1) = {D_1}'(1)+ {D_2}'(1)= 1.642 \hspace{0.05cm}.$$ | ||
:$${D_9}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} | :$${D_9}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} | ||
| − | {D_2}'(9) =-{1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} | + | {D_2}'(9) = - {1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} |
| − | \pi/8} = -0.788$$ | + | \pi/8} = - 0.788$$ |
:$$\Rightarrow D(9) = {D_1}'(9)+ {D_2}'(9)= 0.066 \hspace{0.05cm}.$$}} | :$$\Rightarrow D(9) = {D_1}'(9)+ {D_2}'(9)= 0.066 \hspace{0.05cm}.$$}} | ||
| Zeile 115: | Zeile 122: | ||
$\text{Fazit:}$ | $\text{Fazit:}$ | ||
*Durch diese erste Anwendung des Überlagerungssatzes halbiert sich nahezu der Rechenaufwand. | *Durch diese erste Anwendung des Überlagerungssatzes halbiert sich nahezu der Rechenaufwand. | ||
| − | *Statt $\mathcal{O}= 1920$ benötigt man nur $\mathcal{O} = 2 · 448 + 8 \cdot (4+2) + 16 \cdot 2 = 976$ reelle Operationen. | + | *Statt $\mathcal{O}= 1920$ benötigt man nur noch $\mathcal{O} = 2 · 448 + 8 \cdot (4+2) + 16 \cdot 2 = 976$ reelle Operationen. |
| − | *Der erste Summand berücksichtigt die beiden DFT–Berechnungen mit $N/2 = 8$. | + | *Der erste Summand berücksichtigt die beiden DFT–Berechnungen mit $N/2 = 8$. |
| − | *Der Rest wird für die acht komplexen Multiplikationen und die $16$ komplexen Additionen bzw. Subtraktionen benötigt.}} | + | *Der Rest wird für die acht komplexen Multiplikationen und die $16$ komplexen Additionen bzw. Subtraktionen benötigt.}} |
==Radix-2-Algorithmus nach Cooley und Tukey== | ==Radix-2-Algorithmus nach Cooley und Tukey== | ||
| − | + | <br> | |
| − | Ebenso wie andere FFT–Algorithmen baut das hier vorgestellte Verfahren [CT65]<ref name ='CT65'>Cooley, J.W.; Tukey, J.W.: | + | Ebenso wie andere FFT–Algorithmen baut das hier vorgestellte Verfahren [CT65]<ref name ='CT65'>Cooley, J.W.; Tukey, J.W.: An Algorithm for the Machine Calculation of Complex Fourier Series. <br>In: Mathematics of Computation, Vol. 19, No. 90. (Apr., 1965), pp. 297-301.</ref> von [https://de.wikipedia.org/wiki/James_Cooley James W. Cooley] und [https://en.wikipedia.org/wiki/John_Tukey John W. Tukey] auf dem Überlagerungssatz der DFT auf. Es funktioniert nur dann, wenn die Stützstellenzahl $N$ eine Zweierpotenz ist. |
| − | + | Die Grafik verdeutlicht den Algorithmus für $N = 8$, wobei wieder die Transformation vom Zeit– in den Frequenzbereich dargestellt ist. | |
| + | [[Datei:P_ID1173__Sig_T_5_5_S3a_neu.png|right|frame|frame|Radix-2-Algorithmus (Flussdiagramm)]] | ||
| − | Die | + | *Vor dem eigentlichen FFT-Algorithmus müssen zunächst die Eingangswerte $d(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, d( N - 1)$ im grauen Block „Bitumkehroperation” umsortiert werden. |
| + | *Die Berechnung erfolgt in $\text{log}_2 N = 3$ Stufen, wobei in jeder Stufe $N/2 = 4$ gleiche Berechnungen mit verschiedenen $\mu$–Werten (als Exponent des komplexen Drehfaktors) ausgeführt werden. Eine solche Basisoperation bezeichnet man auch als $\text{Butterfly}$. | ||
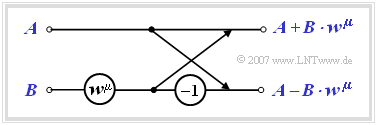
| + | *Jeder Butterfly berechnet aus zwei (im Allgemeinen komplexen) Eingangsgrößen $A$ und $B$ die beiden Ausgangsgrößen $A + B \cdot w^{\mu}$ sowie $A – B \cdot w^{\mu}$ entsprechend der folgenden Skizze. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[Datei:P_ID1174__Sig_T_5_5_S3b_neu.png|center|frame|Butterfly des DFT-Algorithmus]] | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ | ||
| + | Die komplexen Spektralkoeffizienten $D(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, D( N - 1)$ erhält man am Ausgang der letzten Stufe nach Division durch $N$. | ||
| + | *Wie in der [[Aufgaben:Aufgabe_5.5Z:_Rechenaufwand_für_die_FFT|Aufgabe 5.5Z]] gezeigt wird, ergibt sich gegenüber der DFT eine deutlich kürzere Rechenzeit, zum Beispiel für $N = 1024$ um mehr als den Faktor $150$. | ||
| − | + | *Die inverse DFT zur Berechnung der Zeitkoeffizienten aus den Spektralkoeffizienten geschieht mit dem gleichen Algorithmus und nur geringfügigen Modifikationen.}} | |
| − | *Die inverse DFT zur Berechnung der Zeitkoeffizienten aus den Spektralkoeffizienten | ||
| − | + | [[Datei:P_ID1175__Sig_T_5_5_S3c_neu.png|right|frame|Radix-2-Algorithmus (C-Programm)]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 3:}$ | ||
| + | Abschließend wird das C–Programm $\text{fft(N, Re, Im)}$ gemäß dem oben beschriebenen Radix–2–Algorithmus angegeben: | ||
| − | + | *Beim Aufruf beinhalten die beiden Float–Arrays „Re” und „Im” die jeweils $N$ Real– und Imaginärteile der komplexen Zeitkoeffizienten $d(0)$, ... , $d( N - 1)$. | |
| + | *In den gleichen Feldern „Re” und „Im” werden am Programmende die komplexen Koeffizienten $D(0)$, ... , $D( N - 1)$ an das aufrufende Programm zurückgegeben. | ||
| + | *Aufgrund der „In–Place”–Programmierung reichen für diesen Algorithmus $N$ komplexe Speicherplätze aus, allerdings nur, wenn zu Beginn die Eingangswerte umsortiert werden. | ||
| + | *Dies geschieht durch das Programm „bitumkehr”, wobei die Inhalte von ${\rm Re}( \nu)$ und ${\rm Im}( \nu)$ in die Elemente ${\rm Re}( \kappa)$ und ${\rm Im}( \kappa)$ eingetragen werden. Das $\text{Beispiel 4}$ verdeutlicht die Vorgehensweise. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | $\text{Beispiel 4: Bitumkehroperation}$ | |
| + | [[Datei:P_ID1176__Sig_T_5_5_S3d_neu.png|center|frame|Radix-2-Algorithmus $($Bitumkehroperation für $N = 8)$]] | ||
| + | |||
| + | *Der neue Index $\kappa$ ergibt sich, wenn man den Index $\nu$ als Dualzahl schreibt und anschließend die $\text{log}_2 \hspace{0.05cm} N$ Bit in umgekehrter Reihenfolge darstellt. | ||
| + | *Zum Beispiel wird aus $\nu = 3$ der neue Index $\kappa = 6$.}} | ||
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:Aufgabe_5.5:_Fast-Fouriertransformation|Aufgabe 5.5: Fast-Fouriertransformation]] | ||
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_5.5Z:_Rechenaufwand_für_die_FFT|Aufgabe 5.5Z: Rechenaufwand für die FFT]] |
| − | |||
| − | |||
==Quellenverzeichnis== | ==Quellenverzeichnis== | ||
Aktuelle Version vom 21. Mai 2021, 16:12 Uhr
Inhaltsverzeichnis
Rechenaufwand von DFT bzw. IDFT
Ein Nachteil der direkten Berechnung der (im Allgemeinen komplexen) DFT–Zahlenfolgen
- $$\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d(\nu)\hspace{0.1cm} \rangle$$
gemäß den in Kapitel Diskrete Fouriertransformation angegebenen Gleichungen ist der große Rechenaufwand. Wir betrachten als Beispiel die $\rm DFT$, also die Berechnung der Spektralkoeffizienten $D(\mu)$ aus den Zeitkoeffizienten $d(\nu)$:
- $$N \cdot D(\mu) = \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} = d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+\hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}.$$
Der hierfür erforderliche Rechenaufwand soll abgeschätzt werden, wobei wir davon ausgehen, dass die Potenzen des komplexen Drehfaktors $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N}$ bereits in Real– und Imaginärteilform in einer Lookup–Tabelle vorliegen.
Zur Berechnung eines einzelnen Koeffizienten benötigt man dann $N-1$ komplexe Multiplikationen und ebenso viele komplexe Additionen, wobei zu beachten ist:
- Jede komplexe Addition erfordert zwei reelle Additionen:
- $$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.05cm}.$$
- Jede komplexe Multiplikation erfordert vier reelle Multiplikationen und zwei reelle Additionen (eine Subtraktion wird wie eine Addition behandelt):
- $$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot I_1)\hspace{0.05cm}.$$
- Somit sind zur Berechnung aller $N$ Koeffizienten insgesamt die folgende Anzahl $M$ reeller Multiplikationen und die Anzahl $A$ reeller Additionen erforderlich:
- $$M = 4 \cdot N \cdot (N-1),$$
- $$A = 2 \cdot N \cdot (N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$
- In heutigen Rechnern benötigen Multiplikationen und Additionen/Subtraktionen etwa die gleiche Rechenzeit. Es genügt, die Gesamtzahl $\mathcal{O} = M + A$ aller Operationen zu betrachten:
- $$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$
$\text{Fazit:}$
- Man benötigt bereits für eine Diskrete Fouriertransformation $\rm (DFT)$ mit $N = 1000$ knapp acht Millionen Rechenoperationen. Gleiches gilt für eine $\rm IDFT$.
- Mit $N =16 $ sind immerhin noch $1920$ Rechenoperationen erforderlich.
Ist der Parameter $N$ eine Potenz zur Basis $2$, so können rechenzeitgünstigere Algorithmen angewendet werden. Die Vielzahl solcher aus der Literatur bekannten Verfahren werden unter dem Begriff $\text{Fast–Fouriertransformation}$ – abgekürzt $\text{FFT}$ – zusammengefasst. Alle diese Methoden basieren auf dem Überlagerungssatz der DFT.
Überlagerungssatz der DFT
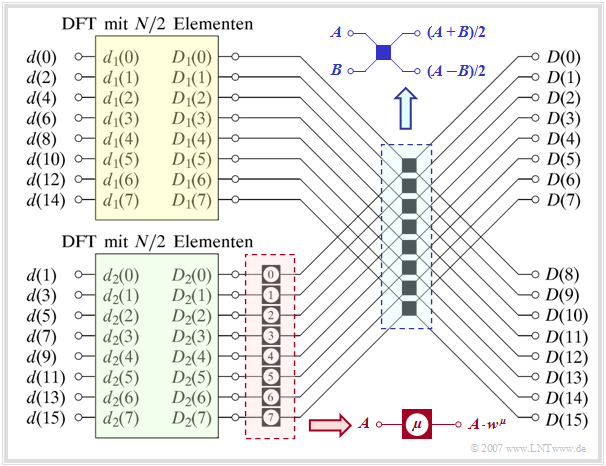
Die Grafik verdeutlicht den so genannten Überlagerungssatz der DFT am Beispiel $N = 16$. Dargestellt ist hier der Übergang vom Zeit– in den Spektralbereich, also die Berechnung der Spektralbereichskoeffizienten aus den Zeitbereichskoeffizienten: $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle.$
Der dadurch beschriebene Algorithmus ist durch folgende Schritte gekennzeichnet:
- Die Folge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ der Länge $N$ wird in zwei Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} d_2(\nu)\hspace{0.1cm}\rangle$ jeweils halber Länge separiert (in der Garafik gelb bzw. grün hinterlegt). Mit $0 \le \nu \lt N/2$ erhält man so die Folgenelemente
- $$d_1(\nu) = d(2\nu), $$
- $$d_2(\nu) = d(2\nu+1) \hspace{0.05cm}.$$
- Die Ausgangsfolgen $\langle \hspace{0.1cm}D_1(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}D_2(\mu )\hspace{0.1cm}\rangle$ der beiden Teilblöcke ergeben sich daraus jeweils durch eine eigene DFT, aber nun nur noch mit halber Länge $N/2 = 8$:
- $$\langle \hspace{0.1cm}D_1(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_1(\nu) \hspace{0.1cm}\rangle , $$
- $$ \langle \hspace{0.1cm}D_2(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_2(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$
- Die Ausgangswerte $\langle \hspace{0.1cm} D_2(\mu )\hspace{0.1cm}\rangle$ der unteren, grünen DFT $($mit $0 \le \mu \lt N/2)$ werden danach im rot umrandeten Block durch komplexe Drehfaktoren hinsichtlich der Phasenlage verändert:
- $$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm wobei}\hspace{0.1cm}w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$
- Jeder einzelne $\text{Butterfly}$ im blau umrandeten Block (in der Grafikmitte) liefert durch Addition bzw. Subtraktion zwei Elemente der gesuchten Ausgangsfolge. Mit $0 \le \mu \lt N/2$ gilt dabei:
- $$D(\mu) = {1}/{2}\cdot \big[D_1(\mu) + D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big],$$
- $$D(\mu +{N}/{2}) = {1}/{2}\cdot \big[D_1(\mu) - D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big]\hspace{0.05cm}.$$
Durch diese erste Anwendung des Überlagerungssatzes halbiert sich somit in etwa der Rechenaufwand.
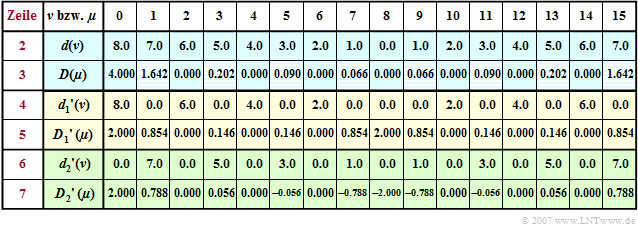
$\text{Beispiel 1:}$ Die DFT–Koeffizienten $d(\nu)$ zur Beschreibung des Zeitverlaufs seien entsprechend der Zeile 2 der folgenden Tabelle „dreieckförmig” belegt. Beachten Sie hierbei die periodische Fortsetzung der DFT, so dass der lineare Anstieg für $t \lt 0$ durch die Koeffizienten $d(8), \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, d(15)$ ausgedrückt wird.
Durch Anwendung des DFT–Algorithmus mit $N = 16$ erhält man die in der Zeile 3 angegebenen Spektralkoeffizienten $D(\mu )$, die bei Vernachlässigung des Aliasingfehlers gleich $D(\mu ) = 4 \cdot \text{si}^2(\pi \cdot \mu/2)$ wären. Man erkennt, dass sich der Aliasingfehler nur auf die ungeradzahligen Koeffizienten auswirkt (schraffierte Felder). Beispielsweise müsste $D(1) = 16/ \pi^2 \approx 1.621\neq 1.642$ sein.
Spaltet man die Gesamtfolge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ in zwei Teilfolgen $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {d_2}'(\nu)\hspace{0.1cm}\rangle$ auf, und zwar derart, dass die erste (gelb hinterlegte) Teilfolge nur geradzahlige Koeffizienten $(\nu = 0,\ 2, \hspace{0.03cm}\text{ ...} \hspace{0.1cm},\ N–2)$ und die zweite (grün hinterlegt) nur ungeradzahlige Koeffizienten $(\nu = 1,\ 3,\ \hspace{0.03cm}\text{ ...} \hspace{0.1cm} ,\ N–1)$ beinhalten und alle anderen zu Null gesetzt sind, so erhält man die zugehörigen Folgen im Spektralbereich:
- $$ \langle \hspace{0.1cm}{D_1}'(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} {d_1}'(\nu) \hspace{0.1cm}\rangle , $$
- $$ \langle \hspace{0.1cm}{D_2}'(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle\hspace{0.1cm} {d_2}'(\nu) \rangle \hspace{0.1cm}\hspace{0.05cm}.$$
In den gelb bzw. grün hinterlegten Zeilen $4\hspace{0.05cm}\text{ ...} \hspace{0.05cm}7$ erkennt man:
- Wegen $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$ gilt auch:
- $$D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu ).$$
- Dies lässt sich zum Beispiel mit dem Additionstheorem linearer Systeme begründen.
- Die Periode der Folge $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ ist aufgrund des Nullsetzens eines jeden zweiten Zeitkoeffizienten nun $N/2$ im Gegensatz zur Periode $N$ der Folge $\langle \hspace{0.1cm} D(\mu )\hspace{0.1cm}\rangle$:
- $${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$
- Die Folge $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ beinhaltet zusätzlich einen Phasenfaktor (aufgrund der Verschiebung um einen Abtastwert), der einen Vorzeichenwechsel zweier um $N/2$ auseinanderliegender Koeffizienten bewirkt:
- $${D_2}'(\mu + {N}/{2}) = - {D_2}'(\mu)\hspace{0.05cm}.$$
- Die Berechnung von $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ ist allerdings ebenso aufwändig wie die Bestimmung von $\langle \hspace{0.1cm}D(\mu )\hspace{0.1cm}\rangle$, da $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}'(\nu)\hspace{0.1cm}\rangle$ ebenfalls aus $N$ Elementen bestehen, auch wenn die Hälfte davon Nullen sind.
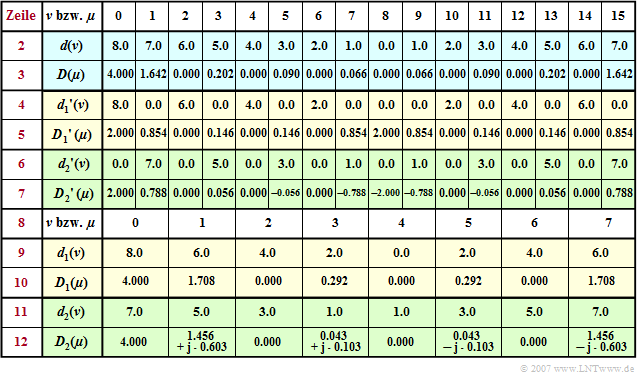
$\text{Beispiel 2:}$ Zur Fortsetzung des ersten Beispiels wird nun die bisherige Tabelle um die Zeilen $8$ bis $12$ erweitert.
Verzichtet man auf die Koeffizienten ${d_1}'(\nu) = 0$ mit ungeraden sowie auf ${d_2}'(\nu) = 0$ mit geraden Indizes, so kommt man zu den Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}d_2(\nu)\hspace{0.1cm}\rangle$ entsprechend den Zeilen $9$ und $11$ . Man erkennt:
- Die Zeitfolgen $\langle \hspace{0.1cm}{d_1}(\nu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}(\nu )\hspace{0.1cm}\rangle$ weisen ebenso wie die dazugehörigen Spektralfolgen $\langle \hspace{0.1cm}{D_1}(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{D_2}(\mu )\hspace{0.1cm}\rangle$ nur noch die Dimension $N/2$ auf.
- Ein Vergleich der Zeilen $5$, $7$, $10$ und $12$ zeigt für $0 \le \mu \lt N/2$ folgenden Zusammenhang:
- $${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu)\hspace{0.05cm},$$
- $$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu)\cdot w^{\hspace{0.04cm}\mu}\hspace{0.05cm}.$$
- Entsprechend ergibt sich für $N/2 \le \mu \lt N$:
- $${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu - {N}/{2})\hspace{0.05cm},$$
- $$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu {-} {N}/{2})\cdot w^{\hspace{0.04cm}\mu}$$
- $$ \Rightarrow \hspace{0.3cm}{D_2}'(\mu) = { - } {1}/{2}\cdot {D_2}(\mu-N/2)\cdot w^{\hspace{0.04cm}\mu {-} N/2}\hspace{0.05cm}. $$
- Zum Beispiel erhält man mit $N = 16$ ⇒ $w = {\rm e}^{ – {\rm j}\hspace{0.04cm} \cdot \hspace{0.04cm}\pi/8}$ für die Indizes $\mu = 1$ bzw. $\mu = 9$:
- $${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} {D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = 0.788$$
- $$\Rightarrow D(1) = {D_1}'(1)+ {D_2}'(1)= 1.642 \hspace{0.05cm}.$$
- $${D_9}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} {D_2}'(9) = - {1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = - 0.788$$
- $$\Rightarrow D(9) = {D_1}'(9)+ {D_2}'(9)= 0.066 \hspace{0.05cm}.$$
$\text{Fazit:}$
- Durch diese erste Anwendung des Überlagerungssatzes halbiert sich nahezu der Rechenaufwand.
- Statt $\mathcal{O}= 1920$ benötigt man nur noch $\mathcal{O} = 2 · 448 + 8 \cdot (4+2) + 16 \cdot 2 = 976$ reelle Operationen.
- Der erste Summand berücksichtigt die beiden DFT–Berechnungen mit $N/2 = 8$.
- Der Rest wird für die acht komplexen Multiplikationen und die $16$ komplexen Additionen bzw. Subtraktionen benötigt.
Radix-2-Algorithmus nach Cooley und Tukey
Ebenso wie andere FFT–Algorithmen baut das hier vorgestellte Verfahren [CT65][1] von James W. Cooley und John W. Tukey auf dem Überlagerungssatz der DFT auf. Es funktioniert nur dann, wenn die Stützstellenzahl $N$ eine Zweierpotenz ist.
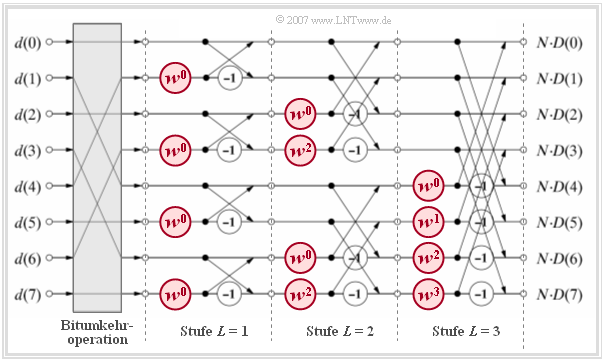
Die Grafik verdeutlicht den Algorithmus für $N = 8$, wobei wieder die Transformation vom Zeit– in den Frequenzbereich dargestellt ist.
- Vor dem eigentlichen FFT-Algorithmus müssen zunächst die Eingangswerte $d(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, d( N - 1)$ im grauen Block „Bitumkehroperation” umsortiert werden.
- Die Berechnung erfolgt in $\text{log}_2 N = 3$ Stufen, wobei in jeder Stufe $N/2 = 4$ gleiche Berechnungen mit verschiedenen $\mu$–Werten (als Exponent des komplexen Drehfaktors) ausgeführt werden. Eine solche Basisoperation bezeichnet man auch als $\text{Butterfly}$.
- Jeder Butterfly berechnet aus zwei (im Allgemeinen komplexen) Eingangsgrößen $A$ und $B$ die beiden Ausgangsgrößen $A + B \cdot w^{\mu}$ sowie $A – B \cdot w^{\mu}$ entsprechend der folgenden Skizze.
$\text{Fazit:}$ Die komplexen Spektralkoeffizienten $D(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, D( N - 1)$ erhält man am Ausgang der letzten Stufe nach Division durch $N$.
- Wie in der Aufgabe 5.5Z gezeigt wird, ergibt sich gegenüber der DFT eine deutlich kürzere Rechenzeit, zum Beispiel für $N = 1024$ um mehr als den Faktor $150$.
- Die inverse DFT zur Berechnung der Zeitkoeffizienten aus den Spektralkoeffizienten geschieht mit dem gleichen Algorithmus und nur geringfügigen Modifikationen.
$\text{Beispiel 3:}$ Abschließend wird das C–Programm $\text{fft(N, Re, Im)}$ gemäß dem oben beschriebenen Radix–2–Algorithmus angegeben:
- Beim Aufruf beinhalten die beiden Float–Arrays „Re” und „Im” die jeweils $N$ Real– und Imaginärteile der komplexen Zeitkoeffizienten $d(0)$, ... , $d( N - 1)$.
- In den gleichen Feldern „Re” und „Im” werden am Programmende die komplexen Koeffizienten $D(0)$, ... , $D( N - 1)$ an das aufrufende Programm zurückgegeben.
- Aufgrund der „In–Place”–Programmierung reichen für diesen Algorithmus $N$ komplexe Speicherplätze aus, allerdings nur, wenn zu Beginn die Eingangswerte umsortiert werden.
- Dies geschieht durch das Programm „bitumkehr”, wobei die Inhalte von ${\rm Re}( \nu)$ und ${\rm Im}( \nu)$ in die Elemente ${\rm Re}( \kappa)$ und ${\rm Im}( \kappa)$ eingetragen werden. Das $\text{Beispiel 4}$ verdeutlicht die Vorgehensweise.
$\text{Beispiel 4: Bitumkehroperation}$
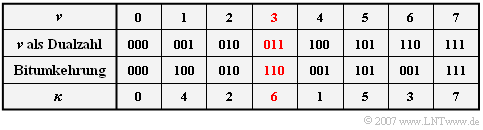
- Der neue Index $\kappa$ ergibt sich, wenn man den Index $\nu$ als Dualzahl schreibt und anschließend die $\text{log}_2 \hspace{0.05cm} N$ Bit in umgekehrter Reihenfolge darstellt.
- Zum Beispiel wird aus $\nu = 3$ der neue Index $\kappa = 6$.
Aufgaben zum Kapitel
Aufgabe 5.5: Fast-Fouriertransformation
Aufgabe 5.5Z: Rechenaufwand für die FFT
Quellenverzeichnis
- ↑ Cooley, J.W.; Tukey, J.W.: An Algorithm for the Machine Calculation of Complex Fourier Series.
In: Mathematics of Computation, Vol. 19, No. 90. (Apr., 1965), pp. 297-301.