Aufgaben:Aufgabe 5.5: Fast-Fouriertransformation: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=*Buch*/*Kapitel* }} 250px|right|* ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="[]"} - Falsch +…“) |
|||
| (22 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signaldarstellung/Fast-Fouriertransformation (FFT) |
}} | }} | ||
| − | [[Datei: | + | [[Datei:P_ID1177__Sig_A_5_5_neu.png|right|frame|FFT-Algorithmus für $N=8$]] |
| + | |||
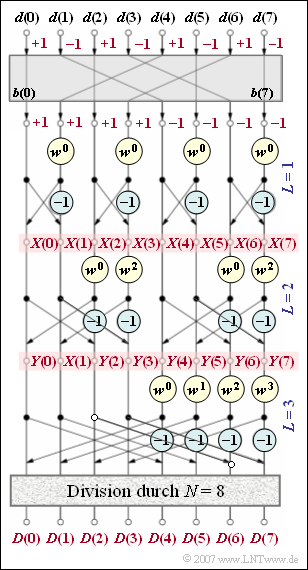
| + | Die Grafik zeigt den Signalflussplan der Fast-Fouriertransformation $\rm (FFT)$ für $N = 8$. | ||
| + | |||
| + | Aus den Zeitkoeffizienten $d(0), \hspace{0.03cm}\text{...} \hspace{0.1cm}, d(7)$ werden die dazugehörigen Spektralkoeffizienten $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ ermittelt. Für diese gilt mit $0 ≤ μ ≤ 7$: | ||
| + | |||
| + | :$$D(\mu) = \frac{1}{N}\cdot \sum_{\nu = 0 }^{N-1} | ||
| + | d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.05cm} \cdot | ||
| + | \hspace{0.05cm}\mu}\hspace{0.05cm},$$ | ||
| + | |||
| + | wobei der komplexe Drehfaktor $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot | ||
| + | \hspace{0.05cm}2\pi /N}$ zu verwenden ist, also $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot | ||
| + | \hspace{0.05cm}\pi /4}$ für $N = 8$. | ||
| + | |||
| + | *Am Eingang wird die alternierende $±1$–Folge $\langle\hspace{0.05cm} d(ν)\hspace{0.05cm}\rangle$ angelegt. | ||
| + | *Nach der Bitumkehroperation ergibt sich daraus die Folge $\langle \hspace{0.05cm}b(\kappa)\hspace{0.05cm}\rangle$. | ||
| + | |||
| + | |||
| + | Es gilt $b(κ) = d(ν)$, wenn man $ν$ als Dualzahl darstellt und die resultierenden drei Bit als $κ$ in umgekehrter Reihenfolge geschrieben werden. Beispielsweise | ||
| + | * folgt aus $ν = 1$ $($binär $001)$ die Position $κ = 4$ $($binär $100)$, | ||
| + | * verbleibt $d(2)$ an der gleichen Position $2$ $($binär $010)$. | ||
| + | |||
| + | |||
| + | Der eigentliche FFT–Algorithmus geschieht für das Beispiel $N = 8$ in $\log_2 N = 3$ Stufen, die mit $L = 1$, $L =2$ und $L = 3$ bezeichnet werden. Weiter gilt: | ||
| + | * In jeder Stufe sind vier Basisoperationen – so genannte '''Butterflies''' – durchzuführen. | ||
| + | * Die Werte am Ausgang der ersten Stufe werden in dieser Aufgabe mit $X(0),\hspace{0.03cm}\text{...} \hspace{0.1cm} , X(7)$ bezeichnet, <br>die der zweiten mit $Y(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , Y(7)$. | ||
| + | * Nach der dritten und letzten Stufe sind alle Werte noch durch $N$ zu dividieren. Hier liegt dann das endgültige Ergebnis $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ vor. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweis:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fast-Fouriertransformation_(FFT)|Fast-Fouriertransformation (FFT)]]. | ||
| + | |||
| + | |||
| Zeile 9: | Zeile 43: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| + | {Berechnen Sie den DFT–Koeffizienten $D(\mu=3)$. | ||
| + | |type="{}"} | ||
| + | $D(\mu=3) \ = \ $ { 0. } | ||
| + | |||
| + | {Berechnen Sie den DFT–Koeffizienten $D(\mu=4)$. | ||
| + | |type="{}"} | ||
| + | $D(\mu=4) \ = \ $ { 1 3% } | ||
| + | |||
| + | {Ermitteln Sie die Ausgangswerte $X(0)$, ... , $X(7)$ der ersten Stufe. Welche der folgenden Aussagen sind zutreffend? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - Alle $X$–Werte mit geradzahligen Indizes sind gleich $2$. |
| − | + | + | + Alle $X$–Werte mit ungeradzahligen Indizes sind gleich $0$. |
| + | {Ermitteln Sie die Ausgangswerte $Y(0)$, ... , $Y(7)$ der zweiten Stufe. Geben Sie zur Kontrolle die Werte $Y(0)$ und $Y(4)$ ein. | ||
| + | |type="{}"} | ||
| + | $Y(0) \ = \ $ { 4 3% } | ||
| + | $Y(4) \ = \ $ { -4.12--3.88 } | ||
| − | { | + | {Berechnen Sie alle $N$ Spektralwerte $D(\mu)$, insbesondere |
|type="{}"} | |type="{}"} | ||
| − | + | $D(\mu = 3) \ = \ $ { 0. 3% } | |
| + | $D(\mu = 4) \ = \ $ { 1 } | ||
| + | {Welche Spektralkoeffizienten würden sich für $d(ν = 4) = 1$ und $d(ν \neq 4) = 0$ ergeben? <br>Geben Sie zur Kontrolle die Werte $D(\mu=3)$ und $D(\mu=4)$ ein. | ||
| + | |type="{}"} | ||
| + | $D(\mu = 3) \ = \ $ { -1.03--0.97 } | ||
| + | $D(\mu = 4) \ = \ $ { 1 3% } | ||
| Zeile 24: | Zeile 76: | ||
===Musterlösung=== | ===Musterlösung=== | ||
| + | |||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''(1)''' Entsprechend der auf dem Angabenblatt gegebenen allgemeinen DFT–Gleichung gilt mit $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot |
| + | \hspace{0.05cm}\pi /4}$ unter Berücksichtigung der alternierenden Zeitkoeffizienten: | ||
| + | |||
| + | :$$8 \cdot D(3) = w^0 - w^3 + w^6- w^9+ w^{12}- w^{15}+ w^{18}- | ||
| + | w^{21} = w^0 - w^3 + w^2- w^1+ w^{4}- w^{7}+ w^{6}- | ||
| + | w^{5}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Hierbei ist berücksichtigt, dass aufgrund der Periodizität $w_9 = w_1$, $w_{12} = w_4$, $w_{15} = w_7$, $w_{18} = w_2$ und $w_{21} = w_5$ ist. | ||
| + | *Nach Umsortieren gilt in gleicher Weise: | ||
| + | |||
| + | :$$8 \cdot D(3) = (w^0 + w^4) - (w^1 + w^5)+ (w^2 + w^6) - (w^3 + w^7) = (1 + w + w^2+ w^3) \cdot (w^0 + w^4)\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Wegen $w_0 = 1$ und $w_4 = \text{e}^{-\text{j}\pi } = \hspace{0.08cm} - \hspace{-0.08cm}1$ erhält man somit $\underline {D(\mu=3) = 0}$. | ||
| + | |||
| + | |||
| + | '''(2)''' In analoger Weise zur Teilaufgabe '''(1)''' ergibt sich nun: | ||
| + | |||
| + | :$$ 8 \cdot D(4) = w^0 - w^4 + w^8- w^{12}+ w^{16}- w^{20}+ | ||
| + | w^{24}- w^{28}= 4 \cdot (w^0 - w^4)= 8 \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{D(\mu=4) = 1}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | [[Datei:P_ID1178__Sig_A_5_5c_neu.png|right|frame|Beispiel für den FFT-Algorithmus]] | ||
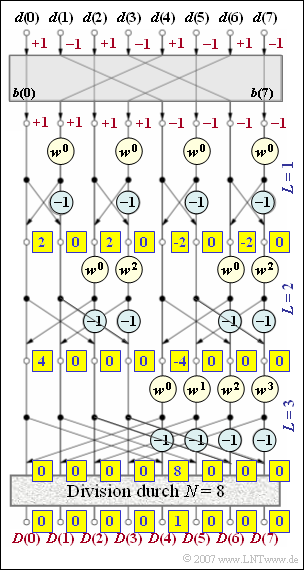
| + | '''(3)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | ||
| + | *Der Term $w^0 = 1$ muss nicht berücksichtigt werden. | ||
| + | *Alle Ausgangswerte mit ungeraden Indizes sind durch die Subtraktion zweier identischer Eingangswerte Null. | ||
| + | *Die erste Aussage trifft nicht zu: Es gilt $X(0) = X(2) = +2$ und $X(4) = X(6) = - 2$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Auf die Multiplikation mit $w^{2} = -{\rm j}$ kann verzichtet werden, da im Signalflussplan die entsprechenden Eingangsgrößen Null sind. | ||
| + | *Man erhält somit $Y(0) \;\underline{= 4}$ und $Y(4) \;\underline{= - \hspace{-0.03cm}4}$. | ||
| + | *Alle anderen Werte sind Null. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Wegen $Y(5) = Y(6) =Y(7) = 0$ spielen auch in der dritten Stufe die Multiplikationen mit $w$, $w^2$ und $w^3$ keine Rolle. Alle Spektralkoeffizienten $D(\mu)$ ergeben sich deshalb zu Null mit Ausnahme von | ||
| + | |||
| + | :$$\hspace{0.15 cm}\underline{D(\mu= 4)} = {1}/{N}\cdot \left[Y(0) - Y(4) \right ] \hspace{0.15 cm}\underline{= 1} | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$\hspace{0.15 cm}\underline{D(\mu =3)} = D(\mu \ne 4) \hspace{0.15 cm}\underline{= 0} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Dieses Ergebnis stimmt mit den Ergebnissen aus '''(1)''' und '''(2)''' überein. | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Nachdem sowohl die Zeitkoeffizienten $d(ν)$ als auch alle Spektralkoeffizienten $D(\mu)$ rein reell sind, besteht kein Unterschied zwischen der FFT und der IFFT. | ||
| + | *Das bedeutet gleichzeitig: Die Eingangs– und Ausgangswerte können vertauscht werden. | ||
| + | |||
| + | *Die Teilaufgabe '''(5)''' hat das folgende Ergebnis geliefert: | ||
| + | |||
| + | :$$d({\rm gerades}\hspace{0.15cm}\nu) = +1, \hspace{0.2cm}d({\rm | ||
| + | ungerades}\hspace{0.15cm}\nu)= -1$$ | ||
| + | :$$\Rightarrow | ||
| + | \hspace{0.3cm}D(\mu = 4)= 1,\hspace{0.2cm}D(\mu \ne 4)= 0.$$ | ||
| + | |||
| + | *Durch Vertauschen der Eingangs– und Ausgangswerte kommt man zur Aufgabenstellung '''(6)''': | ||
| + | |||
| + | :$$d(\nu = 4)= 1, \hspace{0.2cm}d(\nu \ne 4)= 0 \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}D({\rm gerades}\hspace{0.15cm}\mu) = +1, | ||
| + | \hspace{0.2cm}D({\rm ungerades}\hspace{0.15cm}\mu)= -1 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Insbesondere ergibt sich sich $D(\mu=3) \; \underline{= -1}$ und $D(\mu=4) \; \underline{= +1}$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category:Aufgaben zu Signaldarstellung|^ | + | [[Category:Aufgaben zu Signaldarstellung|^5. Zeit- und frequenzdiskrete Signaldarstellung^]] |
Aktuelle Version vom 21. Mai 2021, 17:03 Uhr
Die Grafik zeigt den Signalflussplan der Fast-Fouriertransformation $\rm (FFT)$ für $N = 8$.
Aus den Zeitkoeffizienten $d(0), \hspace{0.03cm}\text{...} \hspace{0.1cm}, d(7)$ werden die dazugehörigen Spektralkoeffizienten $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ ermittelt. Für diese gilt mit $0 ≤ μ ≤ 7$:
- $$D(\mu) = \frac{1}{N}\cdot \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu}\hspace{0.05cm},$$
wobei der komplexe Drehfaktor $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}2\pi /N}$ zu verwenden ist, also $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}\pi /4}$ für $N = 8$.
- Am Eingang wird die alternierende $±1$–Folge $\langle\hspace{0.05cm} d(ν)\hspace{0.05cm}\rangle$ angelegt.
- Nach der Bitumkehroperation ergibt sich daraus die Folge $\langle \hspace{0.05cm}b(\kappa)\hspace{0.05cm}\rangle$.
Es gilt $b(κ) = d(ν)$, wenn man $ν$ als Dualzahl darstellt und die resultierenden drei Bit als $κ$ in umgekehrter Reihenfolge geschrieben werden. Beispielsweise
- folgt aus $ν = 1$ $($binär $001)$ die Position $κ = 4$ $($binär $100)$,
- verbleibt $d(2)$ an der gleichen Position $2$ $($binär $010)$.
Der eigentliche FFT–Algorithmus geschieht für das Beispiel $N = 8$ in $\log_2 N = 3$ Stufen, die mit $L = 1$, $L =2$ und $L = 3$ bezeichnet werden. Weiter gilt:
- In jeder Stufe sind vier Basisoperationen – so genannte Butterflies – durchzuführen.
- Die Werte am Ausgang der ersten Stufe werden in dieser Aufgabe mit $X(0),\hspace{0.03cm}\text{...} \hspace{0.1cm} , X(7)$ bezeichnet,
die der zweiten mit $Y(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , Y(7)$. - Nach der dritten und letzten Stufe sind alle Werte noch durch $N$ zu dividieren. Hier liegt dann das endgültige Ergebnis $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ vor.
Hinweis:
- Die Aufgabe gehört zum Kapitel Fast-Fouriertransformation (FFT).
Fragebogen
Musterlösung
- $$8 \cdot D(3) = w^0 - w^3 + w^6- w^9+ w^{12}- w^{15}+ w^{18}- w^{21} = w^0 - w^3 + w^2- w^1+ w^{4}- w^{7}+ w^{6}- w^{5}\hspace{0.05cm}.$$
- Hierbei ist berücksichtigt, dass aufgrund der Periodizität $w_9 = w_1$, $w_{12} = w_4$, $w_{15} = w_7$, $w_{18} = w_2$ und $w_{21} = w_5$ ist.
- Nach Umsortieren gilt in gleicher Weise:
- $$8 \cdot D(3) = (w^0 + w^4) - (w^1 + w^5)+ (w^2 + w^6) - (w^3 + w^7) = (1 + w + w^2+ w^3) \cdot (w^0 + w^4)\hspace{0.05cm}.$$
- Wegen $w_0 = 1$ und $w_4 = \text{e}^{-\text{j}\pi } = \hspace{0.08cm} - \hspace{-0.08cm}1$ erhält man somit $\underline {D(\mu=3) = 0}$.
(2) In analoger Weise zur Teilaufgabe (1) ergibt sich nun:
- $$ 8 \cdot D(4) = w^0 - w^4 + w^8- w^{12}+ w^{16}- w^{20}+ w^{24}- w^{28}= 4 \cdot (w^0 - w^4)= 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{D(\mu=4) = 1}\hspace{0.05cm}.$$
(3) Richtig ist der Lösungsvorschlag 2:
- Der Term $w^0 = 1$ muss nicht berücksichtigt werden.
- Alle Ausgangswerte mit ungeraden Indizes sind durch die Subtraktion zweier identischer Eingangswerte Null.
- Die erste Aussage trifft nicht zu: Es gilt $X(0) = X(2) = +2$ und $X(4) = X(6) = - 2$.
(4) Auf die Multiplikation mit $w^{2} = -{\rm j}$ kann verzichtet werden, da im Signalflussplan die entsprechenden Eingangsgrößen Null sind.
- Man erhält somit $Y(0) \;\underline{= 4}$ und $Y(4) \;\underline{= - \hspace{-0.03cm}4}$.
- Alle anderen Werte sind Null.
(5) Wegen $Y(5) = Y(6) =Y(7) = 0$ spielen auch in der dritten Stufe die Multiplikationen mit $w$, $w^2$ und $w^3$ keine Rolle. Alle Spektralkoeffizienten $D(\mu)$ ergeben sich deshalb zu Null mit Ausnahme von
- $$\hspace{0.15 cm}\underline{D(\mu= 4)} = {1}/{N}\cdot \left[Y(0) - Y(4) \right ] \hspace{0.15 cm}\underline{= 1} \hspace{0.05cm},$$
- $$\hspace{0.15 cm}\underline{D(\mu =3)} = D(\mu \ne 4) \hspace{0.15 cm}\underline{= 0} \hspace{0.05cm}.$$
Dieses Ergebnis stimmt mit den Ergebnissen aus (1) und (2) überein.
(6) Nachdem sowohl die Zeitkoeffizienten $d(ν)$ als auch alle Spektralkoeffizienten $D(\mu)$ rein reell sind, besteht kein Unterschied zwischen der FFT und der IFFT.
- Das bedeutet gleichzeitig: Die Eingangs– und Ausgangswerte können vertauscht werden.
- Die Teilaufgabe (5) hat das folgende Ergebnis geliefert:
- $$d({\rm gerades}\hspace{0.15cm}\nu) = +1, \hspace{0.2cm}d({\rm ungerades}\hspace{0.15cm}\nu)= -1$$
- $$\Rightarrow \hspace{0.3cm}D(\mu = 4)= 1,\hspace{0.2cm}D(\mu \ne 4)= 0.$$
- Durch Vertauschen der Eingangs– und Ausgangswerte kommt man zur Aufgabenstellung (6):
- $$d(\nu = 4)= 1, \hspace{0.2cm}d(\nu \ne 4)= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D({\rm gerades}\hspace{0.15cm}\mu) = +1, \hspace{0.2cm}D({\rm ungerades}\hspace{0.15cm}\mu)= -1 \hspace{0.05cm}.$$
- Insbesondere ergibt sich sich $D(\mu=3) \; \underline{= -1}$ und $D(\mu=4) \; \underline{= +1}$.