Aufgaben:Aufgabe 1.2: Entropie von Ternärquellen: Unterschied zwischen den Versionen
Markus (Diskussion | Beiträge) |
|||
| (13 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Informationstheorie | + | {{quiz-Header|Buchseite=Informationstheorie/Gedächtnislose Nachrichtenquellen |
}} | }} | ||
| − | [[Datei: | + | [[Datei:Inf_A_1_2_vers2.png|right|frame|Wahrscheinlichkeiten zweier Ternärquellen]] |
| − | + | Die Entropie einer wertdiskreten gedächtnislosen Nachrichtenquelle mit $M$ möglichen Symbolen lautet: | |
:$$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} | :$$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} | ||
{\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$ | {\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$ | ||
| − | + | Hierbei bezeichnen die $p_\mu$ die Auftrittswahrscheinlichkeiten der einzelnen Symbole bzw. Ereignisse. Im vorliegenden Beispiel werden die Ereignisse $\rm R$(ot), $\rm G$(rün) und $\rm S$(chwarz) genannt. | |
| − | + | *Bei einer binären Quelle mit den Auftrittswahrscheinlichkeiten $p$ und $1-p$ kann hierfür geschrieben werden: | |
:$$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot | :$$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot | ||
| − | {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm}.$$ | + | {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm},\hspace{0.3cm} |
| − | + | {\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$ | |
| + | *Die Entropie einer mehrstufigen Quelle lässt sich häufig mit dieser „binären Entropiefunktion” $H_{\rm bin}(p)$ ausdrücken. | ||
| + | |||
| − | + | Betrachtet werden in dieser Aufgabe zwei Ternärquellen mit den Symbolwahrscheinlichkeiten gemäß der Grafik: | |
| − | + | * die Quelle $\rm Q_1$ mit $p_{\rm G }= 1/2$, $p_{\rm S }= 1/3$ und $p_{\rm R }= 1/6$, | |
| + | * die Quelle $\rm Q_2$ mit $p_{\rm G }= p$ sowie $p_{\rm S } = p_{\rm R } = (1-p)/2$. | ||
| − | |||
| − | + | Die Ternärquelle $\rm Q_2$ lässt sich auch auf das Roulette anwenden, wenn ein Spieler nur auf die Felder $\rm R$ot, $\rm S$chwarz und $\rm G$rün (die „Null”) setzt. Dieser Spieltyp wird im Fragebogen mit $\text{Roulette 1}$ bezeichnet. | |
| − | + | Dagegen weist $\text{Roulette 2}$ darauf hin, dass der Spieler auf einzelne Zahlen $(0$, ... , $36)$ setzt. | |
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweis:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Gedächtnislose_Nachrichtenquellen|Gedächtnislose Nachrichtenquellen]]. | ||
| + | |||
| Zeile 30: | Zeile 40: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Entropie | + | {Welche Entropie $H$ besitzt die Quelle $\rm \underline{Q_1}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H \ = \ $ { 1.46 3% } $\ \rm bit$ |
| − | {Welche der folgenden Aussagen sind zutreffend, wenn man | + | {Welche der folgenden Aussagen sind zutreffend, wenn man $\rm R$, $\rm G$ und $\rm S$ durch die Zahlenwerte $-1$, $0$ und $+1$ darstellt? |
| − | |type=" | + | |type="()"} |
- Es ergibt sich eine kleinere Entropie. | - Es ergibt sich eine kleinere Entropie. | ||
+ Die Entropie bleibt gleich. | + Die Entropie bleibt gleich. | ||
| Zeile 42: | Zeile 52: | ||
| − | {Bestimmen Sie die Entropie der Quelle | + | {Bestimmen Sie die Entropie der Quelle $\rm \underline{Q_2}$ unter Verwendung der binären Entropiefunktion $H_{\rm bin}(p)$. Welcher Wert ergibt sich für $\underline{p = 0.5}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H \ = \ $ { 1.5 3% } $\ \rm bit$ |
| − | {Für welchen | + | {Für welchen $p$–Wert der Quelle $\rm \underline{Q_2}$ ergibt sich die maximale Entropie: $H → H_\text{max}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p \ = \ $ { 0.333 3% } |
| − | {Welche Entropie hat die Nachrichtenquelle & | + | {Welche Entropie hat die Nachrichtenquelle $\text{Roulette 1}$, also hinsichtlich der Ereignisse $\rm R$ot, $\rm S$chwarz und $\rm G$rün (die „Null”)? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H \ = \ $ { 1.152 3% } $\ \rm bit$ |
| − | {Welche Entropie weist & | + | {Welche Entropie weist $\text{Roulette 2}$ auf, also hinsichtlich der Zahlen $0$, ... , $36$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H \ = \ $ { 5.209 3% } $\ \rm bit$ |
| Zeile 67: | Zeile 77: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Mit den Auftrittswahrscheinlichkeiten $1/2$, $1/3$ und $1/6$ erhält man folgenden Entropiewert: | |
| − | :$$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) = | + | :$$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) =(1/2 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(2) + (1/3 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(3) \hspace{0.15cm}\underline {\approx 1.46 \, {\rm bit}} \hspace{0.05cm}.$$ |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(2)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | |
| − | + | * Die Entropie hängt nur von den Auftrittswahrscheinlichkeiten ab. | |
| − | + | *Es ist dabei egal, welche Zahlenwerte oder physikalische Größen man den einzelnen Symbolen zuordnet. | |
| − | + | *Anders ist es bei Mittelwerten oder der AKF–Berechnung. Werden nur Symbole angegeben, so kann man hierfür keine Momente angeben. | |
| + | *Außerdem hängen die Mittelwerte, Autokorrelation, usw. davon ab, ob man die Zuordnung bipolar $(-1, \hspace{0.10cm}0, \hspace{0.05cm}+1)$ oder unipolar $(0, \hspace{0.05cm}1, \hspace{0.05cm}2)$ vereinbart. | ||
| − | : | + | |
| + | |||
| + | '''(3)''' Die Entropie der Quelle $\rm Q_2$ lässt sich wie folgt ausdrücken: | ||
| + | :$$H \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ 2 \cdot \frac{1-p}{2} \cdot {\rm log}_2\hspace{0.1cm}\frac {2}{1-p}= p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{1-p} + (1-p)\cdot {\rm log}_2\hspace{0.1cm}(2)= H_{\rm bin}(p) + 1-p \hspace{0.05cm}.$$ | ||
| + | *Für $p = 0.5$ ⇒ $H_{\rm bin}(p) = 1$ ergibt sich $\underline{H = 1.5\hspace{0.05cm}\rm bit}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Die maximale Entropie einer gedächtnislosen Quelle mit dem Symbolumfang $M$ ergibt sich, wenn alle $M$ Symbole gleichwahrscheinlich sind. | ||
| + | *Für den Sonderfall $M=3$ folgt daraus: | ||
:$$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | :$$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| − | \underline {p = 1/3}\hspace{0.05cm}.$$ | + | \underline {p = 1/3 \approx 0.333}\hspace{0.05cm}.$$ |
| − | + | *Damit erhält man mit dem Ergebnis der Teilaufgabe '''(3)''' die folgende Entropie: | |
| − | :$$H | + | :$$H = H_{\rm bin}(1/3) + 1-1/3 = 1/3 \cdot |
| − | {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 | + | {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 $$ |
| − | + | :$$\Rightarrow \hspace{0.3cm}H = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot | |
{\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = | {\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = | ||
{\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} | {\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | |||
| + | '''(5)''' Das System $\text{Roulette 1}$ ist informationstheoretisch gleich der Konfiguration $\rm Q_2$ mit $p = 1/37$: | ||
:$$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$ | :$$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$ | ||
| − | + | *Damit erhält man mit dem Ergebnis der Teilaufgabe '''(3)''': | |
| − | :$$H | + | :$$H = H_{\rm bin}(1/37) + \frac{36}{37} = \frac{1}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) - \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}36 + \frac{36}{37} = |
| − | + | {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot ( 1- {\rm log}_2\hspace{0.1cm}(36)) = 5.209 - 4.057 \hspace{0.15cm} \underline { = 1.152 \, {\rm bit}} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | |||
| + | '''(6)''' Setzt man bei Roulette auf einzelne Zahlen ⇒ Konfiguration $\text{Roulette 2}$, so sind alle Zahlen von $0$ bis $36$ gleichwahrscheinlich und man erhält: | ||
:$$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} | :$$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Aktuelle Version vom 16. Juni 2021, 15:54 Uhr
Die Entropie einer wertdiskreten gedächtnislosen Nachrichtenquelle mit $M$ möglichen Symbolen lautet:
- $$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} {\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$
Hierbei bezeichnen die $p_\mu$ die Auftrittswahrscheinlichkeiten der einzelnen Symbole bzw. Ereignisse. Im vorliegenden Beispiel werden die Ereignisse $\rm R$(ot), $\rm G$(rün) und $\rm S$(chwarz) genannt.
- Bei einer binären Quelle mit den Auftrittswahrscheinlichkeiten $p$ und $1-p$ kann hierfür geschrieben werden:
- $$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm},\hspace{0.3cm} {\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$
- Die Entropie einer mehrstufigen Quelle lässt sich häufig mit dieser „binären Entropiefunktion” $H_{\rm bin}(p)$ ausdrücken.
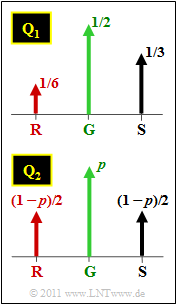
Betrachtet werden in dieser Aufgabe zwei Ternärquellen mit den Symbolwahrscheinlichkeiten gemäß der Grafik:
- die Quelle $\rm Q_1$ mit $p_{\rm G }= 1/2$, $p_{\rm S }= 1/3$ und $p_{\rm R }= 1/6$,
- die Quelle $\rm Q_2$ mit $p_{\rm G }= p$ sowie $p_{\rm S } = p_{\rm R } = (1-p)/2$.
Die Ternärquelle $\rm Q_2$ lässt sich auch auf das Roulette anwenden, wenn ein Spieler nur auf die Felder $\rm R$ot, $\rm S$chwarz und $\rm G$rün (die „Null”) setzt. Dieser Spieltyp wird im Fragebogen mit $\text{Roulette 1}$ bezeichnet.
Dagegen weist $\text{Roulette 2}$ darauf hin, dass der Spieler auf einzelne Zahlen $(0$, ... , $36)$ setzt.
Hinweis:
- Die Aufgabe gehört zum Kapitel Gedächtnislose Nachrichtenquellen.
Fragebogen
Musterlösung
- $$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) =(1/2 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(2) + (1/3 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(3) \hspace{0.15cm}\underline {\approx 1.46 \, {\rm bit}} \hspace{0.05cm}.$$
(2) Richtig ist der Lösungsvorschlag 2:
- Die Entropie hängt nur von den Auftrittswahrscheinlichkeiten ab.
- Es ist dabei egal, welche Zahlenwerte oder physikalische Größen man den einzelnen Symbolen zuordnet.
- Anders ist es bei Mittelwerten oder der AKF–Berechnung. Werden nur Symbole angegeben, so kann man hierfür keine Momente angeben.
- Außerdem hängen die Mittelwerte, Autokorrelation, usw. davon ab, ob man die Zuordnung bipolar $(-1, \hspace{0.10cm}0, \hspace{0.05cm}+1)$ oder unipolar $(0, \hspace{0.05cm}1, \hspace{0.05cm}2)$ vereinbart.
(3) Die Entropie der Quelle $\rm Q_2$ lässt sich wie folgt ausdrücken:
- $$H \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ 2 \cdot \frac{1-p}{2} \cdot {\rm log}_2\hspace{0.1cm}\frac {2}{1-p}= p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{1-p} + (1-p)\cdot {\rm log}_2\hspace{0.1cm}(2)= H_{\rm bin}(p) + 1-p \hspace{0.05cm}.$$
- Für $p = 0.5$ ⇒ $H_{\rm bin}(p) = 1$ ergibt sich $\underline{H = 1.5\hspace{0.05cm}\rm bit}$.
(4) Die maximale Entropie einer gedächtnislosen Quelle mit dem Symbolumfang $M$ ergibt sich, wenn alle $M$ Symbole gleichwahrscheinlich sind.
- Für den Sonderfall $M=3$ folgt daraus:
- $$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {p = 1/3 \approx 0.333}\hspace{0.05cm}.$$
- Damit erhält man mit dem Ergebnis der Teilaufgabe (3) die folgende Entropie:
- $$H = H_{\rm bin}(1/3) + 1-1/3 = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 $$
- $$\Rightarrow \hspace{0.3cm}H = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = {\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} \hspace{0.05cm}.$$
(5) Das System $\text{Roulette 1}$ ist informationstheoretisch gleich der Konfiguration $\rm Q_2$ mit $p = 1/37$:
- $$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$
- Damit erhält man mit dem Ergebnis der Teilaufgabe (3):
- $$H = H_{\rm bin}(1/37) + \frac{36}{37} = \frac{1}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) - \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}36 + \frac{36}{37} = {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot ( 1- {\rm log}_2\hspace{0.1cm}(36)) = 5.209 - 4.057 \hspace{0.15cm} \underline { = 1.152 \, {\rm bit}} \hspace{0.05cm}.$$
(6) Setzt man bei Roulette auf einzelne Zahlen ⇒ Konfiguration $\text{Roulette 2}$, so sind alle Zahlen von $0$ bis $36$ gleichwahrscheinlich und man erhält:
- $$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} \hspace{0.05cm}.$$