Aufgaben:Aufgabe 2.4: Zum LZW-Algorithmus

• Zurück zum Buch

LZW–Wörterbuch für Codierung/Decodierung

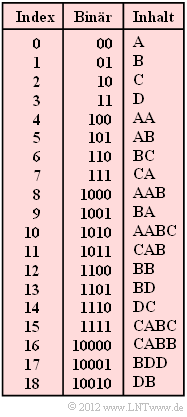
Der Komprimierungsalgorithmus „LZW ” – benannt nach den Erfindern  Abraham Lempel,  Jacob Ziv  und  Terry Welch  – arbeitet ebenso wie „LZ78 ” mit einem globalen Wörterbuch.  Dieses ist hier zu Beginn mit allen möglichen Zeichen – im Beispiel  A,  B,  C,  D  – vorbelegt und wird während der Codierung sukzessive erweitert.

Bei der Decodierung entsteht genau das gleiche Wörterbuch, nur erfolgt der gleiche Eintrag mit dem Index  $I$  einen Schritt später als während der Codierung.  Zur Bezeichnung der Decodierschritte verwenden wir hier die Laufvariable  $i$.

Hier noch einige Hinweise zur LZW–Codierung und –Decodierung:

• Bei der Codierung wird zu jedem Zeitpunkt  $i$  im Wörterbuch nach einer möglichst langen Zeichenkette gesucht, die mit dem aktuell anliegenden Eingabe–String übereinstimmt.
• Der gefundene Wörterbuchindex  $I_i$  wird stets in Binärform übertragen.  Gleichzeitig wird ins Wörterbuch unter dem nächsten freien Index  $W(I_i) + Z$  eingetragen.
• Hierbei bezeichner  $W(I_i)$  ein Zeichen oder eine Zeichenfolge, und  $Z$  ist das erste Zeichen des anstehenden Eingabe–Strings  (also ebenfalls ein Character), das in  $W(I_i)$  nicht mehr berücksichtigt ist.
• Bei  $M = 4$  möglichen Zeichen wird der erste Index  $I_1$  mit zwei Bit übertragen, die Indizes  $I_2$, ... , $I_5$  mit drei Bit, die nächsten acht Indizes mit vier Bit, danach 16 Indizes mit fünf Bit usw.  Die Begründung für diese bitsparende Maßnahme finden Sie in der Musterlösung zu dieser Aufgabe.

Nach der Codierung in der hier beschriebenen Weise über  $16$  Codierschritte ergibt sich die folgende Binärfolge der Länge  $N_{\rm Bit} = 61$:

$$\boldsymbol{\rm 00 \ 000 \ 001 \ 010 \ 100 \ 0001 \ 1000 \ 0111 \ 0001 \ 0001 \ 0011 \ 1011 \ 1011 \ 01101 \ 00011 \ 01001}\hspace{0.05cm}.$$

Aufgabe des Decoders  (genauer gesagt:  Ihre Aufgabe)  ist es nun,

• aus dieser Binärsequenz die Indizes  $I_1$, ... , $I_{16}$  zu rekonstruieren, wobei die unterschiedliche Bitanzahl zu berücksichtigen ist  (Beschreibung der 16 Decodierergebnisse durch Dezimalzahlen),
• anschließend aus dem Wörterbuch entsprechend den Indizes die zugehörigen Zeichen bzw. Zeichenfolgen auszulesen und schließlich – mit einem Schritt Verzögerung – den neuen Wörterbucheintrag zu generieren.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Komprimierung nach Lempel, Ziv und Welch.
• Insbesondere wird Bezug genommen auf die Seiten 

LZ77 – die Grundform der Lempel-Ziv-Algorithmen,

Lempel-Ziv-Codierung mit variabler Indexbitlänge,

Decodierung des LZW-Agorithmus.

• Die  Aufgabe 2.3  sowie die  Aufgabe 2.3Z  behandeln andere LZ-Verfahren in ähnlicher Weise.

Fragebogen

1

Welche Indizes stehen zu den ersten vier Schritten  $i=1$, ... , $i=4$  zur Decodierung an?  Geben Sie alle  $I_i = I(i)$  als Dezimalzahlen ein.

$I_1 \ = \ $

$I_2 \ = \ $

$I_3 \ = \ $

$I_4 \ = \ $

2

Setzen Sie die Unterteilung des Decoder–Eingabestrings bis zum Ende fort.  Welche Indizes ergeben sich bei den Decodierschritten  $i=5$, ... , $i=8$?

$I_5 \ = \ $

$I_6 \ = \ $

$I_7 \ = \ $

$I_8 \ = \ $

3

Wie lautet der Ausgabe–String nach  $i = 16$  Decodierschritten?

	AABCAABAABCAABCABBDBBDCDBA,
	AABCAABAABCABBDCABCABBDDBA,
	AABCAABAABCABDBBABCCDBAABDCDBA.

4

Der nächste Index lautet:   $I_{17} = 10010$ (binär) $= 18$ (dezimal).  Welche der folgenden Aussagen treffen zu?

	Die Decoderausgabe zum Schritt  $i = 17$  lautet  DB.
	Die Decoderausgabe zum Schritt  $i = 17$  lautet  BAD.
	Neuer Wörterbucheintrag  DB  in die Zeile  $I = 19$.
	Neuer Wörterbucheintrag  BAD  in die Zeile  $I = 19$.

5

Der Decoder–Eingabestring bestehe aus  $N_{\rm Bit} = 300$  Binärzeichen (Bit).  Welche der folgenden Aussagen sind dann sicher zutreffend?

	Übertragen wurden  $58$  LZW–Phrasen mit variabler Bitlänge.
	Mit einheitlicher Indexbitlänge wären weniger Bit erforderlich.
	Übertragen wurde eine Datei mit  $N =150$  Quaternärzeichen.

Musterlösung

Musterlösung

(1)  Bei der LZW–Codierung des ersten Zeichens  $(i = 1)$  sind nur die vier Indizes  $I = 0$, ... , $I = 3$  möglich, für die bereits zum Schritt  $i = 0$  (Vorbelegung) ein Wörterbucheintrag vorgenommen wurde. Deshalb genügt es hier, den Index mit zwei Bit zu übertragen.

• Bereits zum Schritt  $i = 2$  werden dagegen drei Bit benötigt. Hätte die Eingangsfolge mit  AAA  begonnen, so hätte die LZW–Codierung  $I_2 = I(i = 2)$  den Dezimalwert  $4$  ergeben. Dieser ist nicht mehr mit zwei Bit darstellbar und muss mit drei Bit codiert werden, ebenso wie  $I_3$,  $I_4$  und  $I_5$.

• Der vorgegebene Eingabestring

$$\boldsymbol{\rm 00 000 001 010 100 0001}\hspace{0.05cm}...$$

ist deshalb vom Decoder wie folgt aufzuteilen:

$$\boldsymbol{\rm 00 | 000 |001 |010 |100 |0001|}\hspace{0.05cm}...$$

• Die Decoderergebnisse der ersten vier Schritte lauten somit:

• $I_1 =$ 00 (binär)      = 0 (dezimal)   ⇒   A,
• $I_2 =$ 000 (binär)    = 0 (dezimal)   ⇒   A,
• $I_3 =$ 001 (binär)    = 1 (dezimal)   ⇒   B,
• $I_4 =$ 010 (binär)    = 2 (dezimal)   ⇒   C.

(2)  Berücksichtigt man, dass

• für  $i = 1$  zwei Bit verwendet werden,
• für  $2 ≤ i ≤ 5$  drei Bit,
• für  $6 ≤ i ≤ 19$  vier Bit,
• für  $14 ≤ i ≤ 29$  fünf Bit,

so kommt man vom „kontinuierlichen Decoder–Eingangsstring”

$$\boldsymbol{\rm 00 000 001 010 100 0001 1000 0111 0001 0001 0011 1011 1011 01101 00011 01001}$$

zum „eingeteilten Decoder–Eingabestring” $($bezeichnet mit  $I_1$, ... ,  $I_{16})$:

$$\boldsymbol{\rm 00 |000 |001 |010 |100 |0001 |1000 |0111 | 0001 |0001 |0011 |1011 |1011 |01101 |00011 |01001} \hspace{0.1cm}.$$

Damit lauten die gesuchten Ergebnisse für die Decodierschritte  $i = 5$, ... ,  $i = 8$:

• $I_5 =$ 100 (binär)      = 4 (dezimal)   ⇒   AA,
• $I_6 =$ 0001 (binär)    = 1 (dezimal)   ⇒   B,
• $I_7 =$ 1000 (binär)    = 8 (dezimal)   ⇒   AAB,
• $I_8 =$ 0111 (binär)    = 7 (dezimal)   ⇒   CA.

(3)  Richtig is tdie Aussage 2.

• Man erhält folgende Decodierergebnisse (in verkürzter Form):

  $I_{9} = 1$   ⇒   B, $\hspace{0.5cm}I_{10} = 1$   ⇒  B,$\hspace{0.5cm}I_{11} = 3$   ⇒   D,$\hspace{0.5cm}I_{12} = 11$   ⇒   CAB,

  $I_{13} = 11$   ⇒   CAB,$\hspace{0.5cm}I_{14} = 13$   ⇒   BD,$\hspace{0.5cm}I_{15} = 3$   ⇒   D,$\hspace{0.5cm}I_{16} = 9$   ⇒   BA.

(4)  Richtig sind die Aussagen 1 und 4. Begründung:

• Der neu ankommende Index ist  $18$  (dezimal) und im Wörterbuch wird unter dem Index  $I = 18$  der Eintrag  DB  gefunden.
• Zum Decodierschritt  $i = 17$  wird in das Wörterbuch die Zeile  $I = 19$  eingetragen.
• Der Eintrag  BAD  setzt sich zusammen aus dem Decodierergebnis aus Schritt  $i = 16$  $($BA$)$  und dem ersten Zeichen  $($D$)$  des neuen Ergebnisses  DB.

(5)  Richtig ist hier nur die Aussage 1:

• Für die erste Phrase genügen zwei Bit.
• Für die Phrasen  $I_2$, ... , $I_5$  benötigt man drei Bit.
• Für die Phrasen  $I_6$, ... , $I_{13}$  benötigt man vier Bit.
• Für die Phrasen  $I_{14}$, ... , $I_{29}$  benötigt man fünf Bit.
• Für die Phrasen  $I_{30}$, ... , $I_{58}$  benötigt man sechs Bit.

• Damit erhält man für die gesamte Bitanzahl:

$$N_{\rm Bit} = 1 \cdot 2 + 4 \cdot 3 + 8 \cdot 4 + 16 \cdot 5 + 29 \cdot 6 = 300 \hspace{0.05cm}.$$

• Mit einheitlicher Bitlänge (sechs Bit für jeden Index) wären  $58 · 6 = 348$  Bit (also mehr) erforderlich   ⇒   die Aussage 2 ist prinzipiell falsch.

Nun zur dritten Aussage, die ebenfalls nicht zutrifft:

• Bei der uncodierten Übertragung von  $N = 150$  Zeichen aus der Symbolmenge  $\{$ A, \ B, \ C, \ D $\}$  würde man genau  $300$  Bit benötigen. Mit LZW benötigt man sicher mehr Bit, wenn die Quelle redundanzfrei ist  (Zeichen gleichwahrscheinlich und statistisch unabhängig).
• Bei redundanter Quelle mit (beispielsweise)  $H = 1.6$ bit/Quellensymbol kann man die Bitanzahl auf  $N_{\rm Bit} = N \cdot H$  begrenzen, vorausgesetzt, es handelt sich um eine sehr große Datei  $(N \to \infty)$.
• Bei einer eher kleinen Datei – wie hier lediglich mit  $N = 150$  Bit – ist keine Aussage möglich, ob die Bitanzahl  $N_{\rm Bit}$  kleiner, gleich oder größer als  $150 · 1.6 = 240$  sein wird.
• Auch  $N_{\rm Bit} > 300$  ist durchaus möglich.  Dann sollte man auf die „Lempel–Ziv–Komprimierung” besser verzichten.