Aufgaben:Aufgabe 2.6: Zur Huffman-Codierung: Unterschied zwischen den Versionen
Markus (Diskussion | Beiträge) |
|||
| (22 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Informationstheorie | + | {{quiz-Header|Buchseite=Informationstheorie/Entropiecodierung nach Huffman |
}} | }} | ||
| − | [[Datei:P_ID2451__Inf_A_2_6.png|right|]] | + | [[Datei:P_ID2451__Inf_A_2_6.png|right|frame|Huffman–Baumdiagramm]] |
| − | Wir betrachten hier eine Quellensymbolfolge & | + | Wir betrachten hier eine Quellensymbolfolge $\langle q_\nu \rangle$ mit dem Symbolumfang $M = 8$: |
| − | :$$q_{\nu} | + | :$$q_{\nu} \in \{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm B}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm C}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm D}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm E}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm F}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm G}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm H}\hspace{0.05cm} |
\}\hspace{0.05cm}.$$ | \}\hspace{0.05cm}.$$ | ||
| − | Sind die Symbole gleichwahrscheinlich, also | + | Sind die Symbole gleichwahrscheinlich, gilt also $p_{\rm A} = p_{\rm B} =$ ... $ = p_{\rm H} = 1/M$, so macht Quellencodierung keinen Sinn. Bereits mit dem Dualcode $\rm A$ → <b>000</b>, $\rm B$ → <b>001</b>, ... , $\rm H$ → <b>111</b>, erreicht nämlich dann die mittlere Codewortlänge $L_{\rm M}$ ihre untere Schranke $H$ gemäß dem Quellencodierungstheorem $(H$ bezeichnet hierbei die Quellenentropie$)$: |
| − | |||
| − | so macht Quellencodierung keinen Sinn. Bereits mit dem Dualcode | ||
:$$L_{\rm M,\hspace{0.08cm}min} = H = 3 \hspace{0.15cm}{\rm bit/Quellensymbol} \hspace{0.05cm}.$$ | :$$L_{\rm M,\hspace{0.08cm}min} = H = 3 \hspace{0.15cm}{\rm bit/Quellensymbol} \hspace{0.05cm}.$$ | ||
| − | |||
Die Symbolwahrscheinlichkeiten seien aber in dieser Aufgabe wie folgt gegeben: | Die Symbolwahrscheinlichkeiten seien aber in dieser Aufgabe wie folgt gegeben: | ||
:$$p_{\rm A} \hspace{-0.05cm}= \hspace{-0.05cm} 0.04 \hspace{0.05cm},\hspace{0.1cm}p_{\rm B} \hspace{-0.05cm}= \hspace{-0.05cm} 0.08 \hspace{0.05cm},\hspace{0.1cm}p_{\rm C} \hspace{-0.05cm}= \hspace{-0.05cm} 0.14 \hspace{0.05cm},\hspace{0.1cm} | :$$p_{\rm A} \hspace{-0.05cm}= \hspace{-0.05cm} 0.04 \hspace{0.05cm},\hspace{0.1cm}p_{\rm B} \hspace{-0.05cm}= \hspace{-0.05cm} 0.08 \hspace{0.05cm},\hspace{0.1cm}p_{\rm C} \hspace{-0.05cm}= \hspace{-0.05cm} 0.14 \hspace{0.05cm},\hspace{0.1cm} | ||
| − | p_{\rm D} \hspace{-0.05cm}= \hspace{-0.05cm} 0.25 \hspace{0.05cm}, | + | p_{\rm D} \hspace{-0.05cm}= \hspace{-0.05cm} 0.25 \hspace{0.05cm},\hspace{0.1cm} p_{\rm E} \hspace{-0.05cm}= \hspace{-0.05cm} 0.24 \hspace{0.05cm},\hspace{0.1cm}p_{\rm F} \hspace{-0.05cm}= \hspace{-0.05cm} 0.12 \hspace{0.05cm},\hspace{0.1cm}p_{\rm G} \hspace{-0.05cm}= \hspace{-0.05cm} 0.10 \hspace{0.05cm},\hspace{0.1cm} |
| − | |||
p_{\rm H} \hspace{-0.05cm}= \hspace{-0.05cm} 0.03 \hspace{0.05cm}.$$ | p_{\rm H} \hspace{-0.05cm}= \hspace{-0.05cm} 0.03 \hspace{0.05cm}.$$ | ||
| − | Es liegt hier also eine redundante Nachrichtenquelle vor, die man durch Huffman–Codierung komprimieren kann. | + | *Es liegt hier also eine redundante Nachrichtenquelle vor, die man durch Huffman–Codierung komprimieren kann. |
| + | *Dieser Algorithmus wurde 1952 – also kurz nach Shannons bahnbrechenden Arbeiten zur Informationstheorie – von [https://de.wikipedia.org/wiki/David_A._Huffman David Albert Huffman] veröffentlicht und erlaubt die Konstruktion von optimalen präfixfreien Codes. | ||
| − | |||
| − | : | + | Der Algorithmus soll hier ohne Herleitung und Beweis angegeben werden, wobei wir uns auf Binärcodes beschränken ⇒ die Codesymbolfolge besteht nur aus Nullen und Einsen: |
| − | : | + | :'''(1)''' Man ordne die Symbole nach fallenden Auftrittswahrscheinlichkeiten. |
| − | : | + | :'''(2)''' Man fasse die zwei unwahrscheinlichsten Symbole zu einem neuen Symbol zusammen. |
| − | : | + | :'''(3)''' Man wiederhole Schritt '''(1)''' und '''(2)''', bis nur zwei (zusammengefasste) Symbole übrig bleiben. |
| − | : | + | :'''(4)''' Die wahrscheinlichere Symbolmenge wird mit <b>1</b> binär codiert, die andere Menge mit <b>0</b>. |
| − | + | :'''(5)''' Man ergänze schrittweise (von unten nach oben) die aufgespaltenen Teilcodes mit <b>1</b> bzw. <b>0</b>. | |
| − | |||
| − | + | Oft wird dieser Algorithmus durch ein Baumdiagramm veranschaulicht. Die Grafik zeigt dieses für den vorliegenden Fall. | |
| − | : | + | Sie haben folgende Aufgaben: |
| + | |||
| + | :'''(a)''' Zuordnung der Symbole $\rm A$, ... , $\rm H$ zu den mit '''[1]''', ... , '''[8]''' bezeichneten Eingängen. | ||
| + | |||
| + | :'''(b)''' Bestimmung der Summenwahrscheinlichkeiten $U$, ... , $Z$ sowie $R$ („Root”). | ||
| + | |||
| + | :'''(c)''' Zuordnung der Symbole $\rm A$, ... , $\rm H$ zu den entsprechenden Huffman–Binärfolgen. Eine rote Verbindung entspricht einer <b>1</b>, eine blaue Verbindung einer <b>0</b>. | ||
Sie werden feststellen, dass die mittlere Codewortlänge | Sie werden feststellen, dass die mittlere Codewortlänge | ||
:$$L_{\rm M} = \sum_{\mu = 1}^{M}\hspace{0.05cm} p_{\mu} \cdot L_{\mu} $$ | :$$L_{\rm M} = \sum_{\mu = 1}^{M}\hspace{0.05cm} p_{\mu} \cdot L_{\mu} $$ | ||
| − | bei Huffman–Codierung nur unwesentlich größer ist als die Quellenentropie | + | bei Huffman–Codierung nur unwesentlich größer ist als die Quellenentropie $H$. In dieser Gleichung gelten für den vorliegenden Fall folgende Werte: |
| + | *$M = 8$, $p_1 = p_{\rm A}$, ... , $p_8 = p_{\rm H}$. | ||
| + | *Die jeweilige Bitanzahl der Codesymbole für $\rm A$, ... , $\rm H$ ist mit $L_1$, ... , $L_8$ bezeichnet. | ||
| − | |||
| − | |||
| − | : | + | |
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Entropiecodierung_nach_Huffman|Entropiecodierung nach Huffman]]. | ||
| + | *Insbesondere wird Bezug genommen auf die Seiten | ||
| + | ** [[Informationstheorie/Entropiecodierung_nach_Huffman#Der_Huffman.E2.80.93Algorithmus|Der Huffman-Algorithmus]], | ||
| + | **[[Informationstheorie/Entropiecodierung_nach_Huffman#Darstellung_des_Huffman.E2.80.93Codes_als_Baumdiagramm|Darstellung des Huffman-Codes als Baumdiagramm]]. | ||
| + | *Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das folgende Interaktionsmodul: [[Applets:Huffman_Shannon_Fano|Huffman- und Shannon-Fano-Codierung ⇒ $\text{SWF}$–Version]]. | ||
| + | |||
| Zeile 56: | Zeile 67: | ||
{Welche Eingänge im Baumdiagramm stehen für | {Welche Eingänge im Baumdiagramm stehen für | ||
|type="{}"} | |type="{}"} | ||
| − | + | Eingangsnummer $ \ = \ $ { 7 } ⇒ Symbol $\rm A$ | |
| − | + | Eingangsnummer $ \ = \ $ { 6 } ⇒ Symbol $\rm B$ | |
| − | + | Eingangsnummer $ \ = \ $ { 3 } ⇒ Symbol $\rm C$ | |
| − | + | Eingangsnummer $ \ = \ $ { 1 } ⇒ Symbol $\rm D$ | |
| − | {Welche Zahlenwerte sollten bei den Knoten im Baumdiagramm stehen? | + | {Welche Zahlenwerte (Wahrscheinlichkeiten) sollten bei den Knoten im Baumdiagramm stehen? |
|type="{}"} | |type="{}"} | ||
| − | Knoten U = { 0. | + | Wahrscheinlichkeit $ \ = \ $ { 0.07 1% } bei Knoten $\rm U$ |
| − | Knoten V = { 0. | + | Wahrscheinlichkeit $ \ = \ $ { 0.15 1% } bei Knoten $\rm V$ |
| − | Knoten W = { 0. | + | Wahrscheinlichkeit $ \ = \ $ { 0.22 1% } bei Knoten $\rm W$ |
| − | Knoten | + | Wahrscheinlichkeit $ \ = \ $ { 0.29 1% } bei Knoten $\rm X$ |
| − | + | Wahrscheinlichkeit $ \ = \ $ { 0.46 1% } bei Knoten $\rm Y$ | |
| + | Wahrscheinlichkeit $ \ = \ $ { 0.54 1% } bei Knoten $\rm Z$ | ||
| + | Wahrscheinlichkeit $ \ = \ $ { 1 1% } bei $\rm Root$ | ||
| Zeile 74: | Zeile 87: | ||
{Welche Binärcodes (darzustellen mit Nullen und Einsen) ergeben sich für | {Welche Binärcodes (darzustellen mit Nullen und Einsen) ergeben sich für | ||
|type="{}"} | |type="{}"} | ||
| − | + | Binärcode $ \ = \ $ { 11101 } ⇒ Symbol $\rm A$ | |
| − | + | Binärcode $ \ = \ $ { 1111 } ⇒ Symbol $\rm B$ | |
| − | + | Binärcode $ \ = \ $ { 110 } ⇒ Symbol $\rm C$ | |
| − | + | Binärcode $ \ = \ $ { 10 } ⇒ Symbol $\rm D$ | |
{Wie groß ist die mittlere Codewortlänge? | {Wie groß ist die mittlere Codewortlänge? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $L_{\rm M} \ = \ $ { 2.73 3% } $\ \rm bit/Quellensymbol$ |
| − | {Wie groß ist die Quellenentropie | + | {Wie groß ist die Quellenentropie $H$? |
| − | |type=" | + | |type="()"} |
| − | + H = 2.71 bit/Quellensymbol. | + | + $H = 2.71\ \rm bit/Quellensymbol.$ |
| − | - H = 2.75 bit/Quellensymbol. | + | - $H = 2.75\ \rm bit/Quellensymbol.$ |
| − | - H = 3.00 bit/Quellensymbol. | + | - $H = 3.00\ \rm bit/Quellensymbol.$ |
| Zeile 97: | Zeile 110: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Vor dem Huffman–Algorithmus müssen die Symbole nach ihren Auftrittswahrscheinlichkeiten sortiert werden. | |
| + | *Da die zwei unwahrscheinlichsten Symbole schon im ersten Schritt zusammengefasst werden, nehmen die Auftrittswahrscheinlichkeiten von oben nach unten ab <br>(in der Grafik zu dieser Musterlösung von links nach rechts). | ||
| + | *Durch Vergleich mit dem Angabenblatt erhält man: | ||
| + | |||
| + | :Symbol $\rm A$: <u>Eingang 7</u>, Symbol $\rm B$: <u>Eingang 6</u>, Symbol $\rm C$: <u>Eingang 3</u>, Symbol $\rm D$: <u>Eingang 1</u>. | ||
| + | |||
| + | [[Datei:P_ID2452__Inf_A_2_6a.png|right|right|frame|An die Aufgabe angepasstes Baumdiagramm]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Der Knoten $\rm R$ ist die Baumwurzel (<i>Root</i>). Dieser ist stets mit $\underline{R=1}$ belegt, unabhängig von den Auftrittswahrscheinlichkeiten. | ||
| − | : | + | Für die weiteren Werte gilt: |
| − | |||
| − | + | :Schritt 1: $p_{\rm U} = p_{\rm A} + p_{\rm H} = 0.04 + 0.03 \hspace{0.15cm}\underline{ =0.07}$, | |
| − | :Schritt | + | :Schritt 2: $p_{\rm V} = p_{\rm U} + p_{\rm B} = 0.07 + 0.08 \hspace{0.15cm}\underline{ =0.15}$, |
| − | :Schritt | + | :Schritt 3: $p_{\rm W} = p_{\rm F} + p_{\rm G} = 0.12 + 0.10 \hspace{0.15cm}\underline{ =0.22}$, |
| − | :Schritt | + | :Schritt 4: $p_{\rm X} = p_{\rm V} + p_{\rm C} = 0.15 + 0.14 \hspace{0.15cm}\underline{ =0.29}$, |
| − | :Schritt | + | :Schritt 5: $p_{\rm Y} = p_{\rm W} + p_{\rm E} = 0.22 + 0.24 \hspace{0.15cm}\underline{ =0.46}$, |
| − | :Schritt | + | :Schritt 6: $p_{\rm Z} = p_{\rm X} + p_{\rm D} = 0.29 + 0.25 \hspace{0.15cm}\underline{ =0.54}$. |
| + | <br clear=all> | ||
| + | '''(3)''' Den Huffman–Code für das Symbol $\rm A$ erhält man, wenn man den Weg von der $\rm Root$ (gelber Punkt) zum Symbol $\rm A$ zurückverfolgt und jeder roten Verbindungslinie eine <b>1</b> zuordnet, jeder blauen eine <b>0</b>. | ||
| − | + | * Symbol $\rm A$: rot–rot–rot–blau–rot → <b><u>11101</u></b>, | |
| − | + | * Symbol $\rm B$: rot–rot–rot–rot → <b><u>1111</u></b>, | |
| − | |||
| − | + | * Symbol $\rm C$: rot–rot–blau → <b><u>110</u></b>, | |
| − | + | * Symbol $\rm D$: rot–blau– → <b><u>10</u></b>, | |
| − | + | * Symbol $\rm E$: blau–rot → <b>01</b>, | |
| − | + | * Symbol $\rm F$: blau–blau–rot → <b>001</b>, | |
| − | + | * Symbol $\rm G$: blau–blau–blau → <b>000</b>, | |
| − | + | * Symbol $\rm H$: rot–rot–rot–blau–blau → <b>11100</b>. | |
| − | |||
| − | + | '''(4)''' Die Codierung unter Punkt '''(3)''' hat ergeben, dass | |
| − | + | * die Symbole $\rm D$ und $\rm E$ mit zwei Bit, | |
| − | + | * die Symbole $\rm C$, $\rm F$ und $\rm G$ mit drei Bit, | |
| − | + | * das Symbol $\rm B$ mit vier Bit, und | |
| − | + | * die Symbole $\rm A$ und $\rm H$ jeweils mit fünf Bit | |
| − | |||
| − | : | + | dargestellt werden. Damit erhält man für die mittlere Codewortlänge (in „bit/Quellensymbol”): |
| + | :$$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (p_{\rm D} + p_{\rm E}) \cdot 2 + (p_{\rm C} + p_{\rm F} + p_{\rm G}) \cdot 3 + p_{\rm B} \cdot 4 +(p_{\rm A} + p_{\rm H}) \cdot 5 = 0.49 \cdot 2 + 0.36 \cdot 3 +0.08 \cdot 4 +0.07 \cdot 5 | ||
| + | \hspace{0.15cm}\underline{= 2.73}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Man erkennt, dass | + | '''(5)''' Richtig ist allein die <u>Antwort 1</u>: |
| + | *Die mittlere Codewortlänge $L_{\rm M}$ kann nicht kleiner sein als die Quellenentropie $H$. Damit scheiden die Antworten 2 und 3 aus. | ||
| + | *Aus den vorgegebenen Auftrittswahrscheinlichkeiten kann die Quellenentropie tatsächlich zu $H = 2.71$ bit/Quellensymbol berechnet werden. | ||
| + | *Man erkennt, dass diese Huffman–Codierung die vorgegebene Grenze (Quellencodierungstheorem) $L_{\rm M, \ min } \ge H = 2.71$ bit/Quellensymbol nahezu erreicht. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 10. August 2021, 15:11 Uhr
Wir betrachten hier eine Quellensymbolfolge $\langle q_\nu \rangle$ mit dem Symbolumfang $M = 8$:
- $$q_{\nu} \in \{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm B}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm C}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm D}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm E}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm F}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm G}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm H}\hspace{0.05cm} \}\hspace{0.05cm}.$$
Sind die Symbole gleichwahrscheinlich, gilt also $p_{\rm A} = p_{\rm B} =$ ... $ = p_{\rm H} = 1/M$, so macht Quellencodierung keinen Sinn. Bereits mit dem Dualcode $\rm A$ → 000, $\rm B$ → 001, ... , $\rm H$ → 111, erreicht nämlich dann die mittlere Codewortlänge $L_{\rm M}$ ihre untere Schranke $H$ gemäß dem Quellencodierungstheorem $(H$ bezeichnet hierbei die Quellenentropie$)$:
- $$L_{\rm M,\hspace{0.08cm}min} = H = 3 \hspace{0.15cm}{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Die Symbolwahrscheinlichkeiten seien aber in dieser Aufgabe wie folgt gegeben:
- $$p_{\rm A} \hspace{-0.05cm}= \hspace{-0.05cm} 0.04 \hspace{0.05cm},\hspace{0.1cm}p_{\rm B} \hspace{-0.05cm}= \hspace{-0.05cm} 0.08 \hspace{0.05cm},\hspace{0.1cm}p_{\rm C} \hspace{-0.05cm}= \hspace{-0.05cm} 0.14 \hspace{0.05cm},\hspace{0.1cm} p_{\rm D} \hspace{-0.05cm}= \hspace{-0.05cm} 0.25 \hspace{0.05cm},\hspace{0.1cm} p_{\rm E} \hspace{-0.05cm}= \hspace{-0.05cm} 0.24 \hspace{0.05cm},\hspace{0.1cm}p_{\rm F} \hspace{-0.05cm}= \hspace{-0.05cm} 0.12 \hspace{0.05cm},\hspace{0.1cm}p_{\rm G} \hspace{-0.05cm}= \hspace{-0.05cm} 0.10 \hspace{0.05cm},\hspace{0.1cm} p_{\rm H} \hspace{-0.05cm}= \hspace{-0.05cm} 0.03 \hspace{0.05cm}.$$
- Es liegt hier also eine redundante Nachrichtenquelle vor, die man durch Huffman–Codierung komprimieren kann.
- Dieser Algorithmus wurde 1952 – also kurz nach Shannons bahnbrechenden Arbeiten zur Informationstheorie – von David Albert Huffman veröffentlicht und erlaubt die Konstruktion von optimalen präfixfreien Codes.
Der Algorithmus soll hier ohne Herleitung und Beweis angegeben werden, wobei wir uns auf Binärcodes beschränken ⇒ die Codesymbolfolge besteht nur aus Nullen und Einsen:
- (1) Man ordne die Symbole nach fallenden Auftrittswahrscheinlichkeiten.
- (2) Man fasse die zwei unwahrscheinlichsten Symbole zu einem neuen Symbol zusammen.
- (3) Man wiederhole Schritt (1) und (2), bis nur zwei (zusammengefasste) Symbole übrig bleiben.
- (4) Die wahrscheinlichere Symbolmenge wird mit 1 binär codiert, die andere Menge mit 0.
- (5) Man ergänze schrittweise (von unten nach oben) die aufgespaltenen Teilcodes mit 1 bzw. 0.
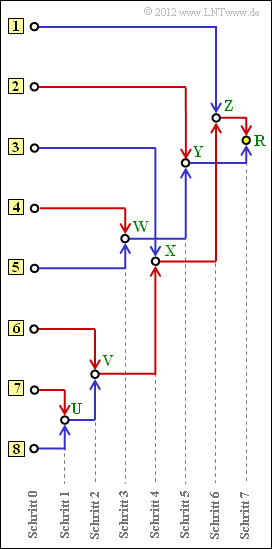
Oft wird dieser Algorithmus durch ein Baumdiagramm veranschaulicht. Die Grafik zeigt dieses für den vorliegenden Fall.
Sie haben folgende Aufgaben:
- (a) Zuordnung der Symbole $\rm A$, ... , $\rm H$ zu den mit [1], ... , [8] bezeichneten Eingängen.
- (b) Bestimmung der Summenwahrscheinlichkeiten $U$, ... , $Z$ sowie $R$ („Root”).
- (c) Zuordnung der Symbole $\rm A$, ... , $\rm H$ zu den entsprechenden Huffman–Binärfolgen. Eine rote Verbindung entspricht einer 1, eine blaue Verbindung einer 0.
Sie werden feststellen, dass die mittlere Codewortlänge
- $$L_{\rm M} = \sum_{\mu = 1}^{M}\hspace{0.05cm} p_{\mu} \cdot L_{\mu} $$
bei Huffman–Codierung nur unwesentlich größer ist als die Quellenentropie $H$. In dieser Gleichung gelten für den vorliegenden Fall folgende Werte:
- $M = 8$, $p_1 = p_{\rm A}$, ... , $p_8 = p_{\rm H}$.
- Die jeweilige Bitanzahl der Codesymbole für $\rm A$, ... , $\rm H$ ist mit $L_1$, ... , $L_8$ bezeichnet.
Hinweise:
- Die Aufgabe gehört zum Kapitel Entropiecodierung nach Huffman.
- Insbesondere wird Bezug genommen auf die Seiten
- Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das folgende Interaktionsmodul: Huffman- und Shannon-Fano-Codierung ⇒ $\text{SWF}$–Version.
Fragebogen
Musterlösung
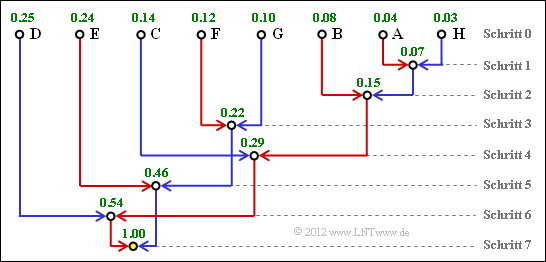
- Da die zwei unwahrscheinlichsten Symbole schon im ersten Schritt zusammengefasst werden, nehmen die Auftrittswahrscheinlichkeiten von oben nach unten ab
(in der Grafik zu dieser Musterlösung von links nach rechts). - Durch Vergleich mit dem Angabenblatt erhält man:
- Symbol $\rm A$: Eingang 7, Symbol $\rm B$: Eingang 6, Symbol $\rm C$: Eingang 3, Symbol $\rm D$: Eingang 1.
(2) Der Knoten $\rm R$ ist die Baumwurzel (Root). Dieser ist stets mit $\underline{R=1}$ belegt, unabhängig von den Auftrittswahrscheinlichkeiten.
Für die weiteren Werte gilt:
- Schritt 1: $p_{\rm U} = p_{\rm A} + p_{\rm H} = 0.04 + 0.03 \hspace{0.15cm}\underline{ =0.07}$,
- Schritt 2: $p_{\rm V} = p_{\rm U} + p_{\rm B} = 0.07 + 0.08 \hspace{0.15cm}\underline{ =0.15}$,
- Schritt 3: $p_{\rm W} = p_{\rm F} + p_{\rm G} = 0.12 + 0.10 \hspace{0.15cm}\underline{ =0.22}$,
- Schritt 4: $p_{\rm X} = p_{\rm V} + p_{\rm C} = 0.15 + 0.14 \hspace{0.15cm}\underline{ =0.29}$,
- Schritt 5: $p_{\rm Y} = p_{\rm W} + p_{\rm E} = 0.22 + 0.24 \hspace{0.15cm}\underline{ =0.46}$,
- Schritt 6: $p_{\rm Z} = p_{\rm X} + p_{\rm D} = 0.29 + 0.25 \hspace{0.15cm}\underline{ =0.54}$.
(3) Den Huffman–Code für das Symbol $\rm A$ erhält man, wenn man den Weg von der $\rm Root$ (gelber Punkt) zum Symbol $\rm A$ zurückverfolgt und jeder roten Verbindungslinie eine 1 zuordnet, jeder blauen eine 0.
- Symbol $\rm A$: rot–rot–rot–blau–rot → 11101,
- Symbol $\rm B$: rot–rot–rot–rot → 1111,
- Symbol $\rm C$: rot–rot–blau → 110,
- Symbol $\rm D$: rot–blau– → 10,
- Symbol $\rm E$: blau–rot → 01,
- Symbol $\rm F$: blau–blau–rot → 001,
- Symbol $\rm G$: blau–blau–blau → 000,
- Symbol $\rm H$: rot–rot–rot–blau–blau → 11100.
(4) Die Codierung unter Punkt (3) hat ergeben, dass
- die Symbole $\rm D$ und $\rm E$ mit zwei Bit,
- die Symbole $\rm C$, $\rm F$ und $\rm G$ mit drei Bit,
- das Symbol $\rm B$ mit vier Bit, und
- die Symbole $\rm A$ und $\rm H$ jeweils mit fünf Bit
dargestellt werden. Damit erhält man für die mittlere Codewortlänge (in „bit/Quellensymbol”):
- $$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (p_{\rm D} + p_{\rm E}) \cdot 2 + (p_{\rm C} + p_{\rm F} + p_{\rm G}) \cdot 3 + p_{\rm B} \cdot 4 +(p_{\rm A} + p_{\rm H}) \cdot 5 = 0.49 \cdot 2 + 0.36 \cdot 3 +0.08 \cdot 4 +0.07 \cdot 5 \hspace{0.15cm}\underline{= 2.73}\hspace{0.05cm}.$$
(5) Richtig ist allein die Antwort 1:
- Die mittlere Codewortlänge $L_{\rm M}$ kann nicht kleiner sein als die Quellenentropie $H$. Damit scheiden die Antworten 2 und 3 aus.
- Aus den vorgegebenen Auftrittswahrscheinlichkeiten kann die Quellenentropie tatsächlich zu $H = 2.71$ bit/Quellensymbol berechnet werden.
- Man erkennt, dass diese Huffman–Codierung die vorgegebene Grenze (Quellencodierungstheorem) $L_{\rm M, \ min } \ge H = 2.71$ bit/Quellensymbol nahezu erreicht.