Aufgaben:Aufgabe 2.6Z: Nochmals zum Huffman–Code: Unterschied zwischen den Versionen
Nabil (Diskussion | Beiträge) |
|||
| (19 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Informationstheorie | + | {{quiz-Header|Buchseite=Informationstheorie/Entropiecodierung nach Huffman |
}} | }} | ||
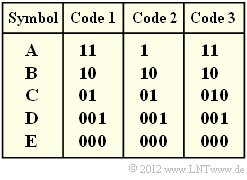
| − | [[Datei:P_ID2453__Inf_Z_2_6.png|right|]] | + | [[Datei:P_ID2453__Inf_Z_2_6.png|right|frame|Drei Binärcodes zur Auswahl ]] |
| − | Der Algorithmus von David | + | Der Algorithmus von [https://de.wikipedia.org/wiki/David_A._Huffman David Albert Huffman] realisiert eine Entropiecodierung mit folgenden Eigenschaften: |
| − | + | * Der entstehende Binärcode ist präfixfrei und somit in einfacher Weise (und sofort) decodierbar. | |
| − | + | * Der Code führt bei gedächtnisloser Quelle zur kleinstmöglichen mittleren Codewortlänge $L_{\rm M}$. | |
| − | + | * $L_{\rm M}$ ist aber nie kleiner als die Quellenentropie $H$. | |
| + | *Diese beiden Größen sind allein aus den $M$ Symbolwahrscheinlichkeiten berechenbar. | ||
| − | |||
| − | < | + | Vorausgesetzt wird für diese Aufgabe eine gedächtnislose Quelle mit dem Symbolumfang $M = 5$ und dem Alphabet |
| + | :$$\{ {\rm A},\ {\rm B},\ {\rm C},\ {\rm D},\ {\rm E} \}.$$ | ||
| + | |||
| + | In obiger Grafik sind drei Codes vorgegeben. Sie sollen entscheiden, welche dieser Codes durch Anwendung des Huffman–Algorithmus entstanden sind (oder sein könnten). | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <u>Hinweise:</u> | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Entropiecodierung_nach_Huffman|Entropiecodierung nach Huffman]]. | ||
| + | *Weitere Informationen zum Huffman–Algorithmus finden Sie auch im Angabenblatt zur [[Aufgaben:2.6_Zur_Huffman-Codierung|Aufgabe 2.6]]. | ||
| + | *Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das Interaktionsmodul: [[Applets:Huffman_Shannon_Fano|Huffman- und Shannon-Fano-Codierung ⇒ $\text{SWF}$–Version]]. | ||
| + | |||
| Zeile 20: | Zeile 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Codes | + | {Welche Codes könnten entsprechend Huffman für $p_{\rm A} = p_{\rm B} = p_{\rm C} = 0.3$ und $p_{\rm D} = p_{\rm E} = 0.05$ entstanden sein? |
|type="[]"} | |type="[]"} | ||
| − | + Code 1, | + | + $\text{Code 1}$, |
| − | - Code 2, | + | - $\text{Code 2}$, |
| − | - Code 3. | + | - $\text{Code 3}$. |
| − | {Wie stehen mittlere Codewortlänge | + | {Wie stehen die mittlere Codewortlänge $L_{\rm M}$ und die Entropie $H$ bei den gegebenen Wahrscheinlichkeiten in Relation? |
| − | |type=" | + | |type="()"} |
| − | - | + | - $L_{\rm M} < H$, |
| − | - | + | - $L_{\rm M} \ge H$, |
| − | + | + | + $L_{\rm M} > H$. |
| − | {Mit welchen Symbolwahrscheinlichkeiten würde | + | {Betrachten Sie den $\text{Code 1}$. Mit welchen Symbolwahrscheinlichkeiten würde $L_{\rm M} = H$ gelten? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\ p_{\rm A} \ = \ $ { 0.25 3% } |
| − | $ | + | $\ p_{\rm B} \ = \ $ { 0.25 3% } |
| − | $ | + | $\ p_{\rm C} \ = \ $ { 0.25 3% } |
| − | $ | + | $\ p_{\rm D} \ = \ $ { 0.125 3% } |
| − | $ | + | $\ p_{\rm E} \ = \ $ { 0.125 3% } |
| − | {Die | + | {Die in der Teilaufgabe '''(3)''' berechneten Wahrscheinlichkeiten gelten weiter. <br>Die mittlere Codewortlänge wird aber nun für eine Folge der Länge $N = 40$ ermittelt ⇒ $L_{\rm M}\hspace{0.03cm}'$. Was ist möglich? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $L_{\rm M}\hspace{0.01cm}' < L_{\rm M}$, |
| − | + | + | + $L_{\rm M}\hspace{0.01cm}' = L_{\rm M}$, |
| − | + | + | + $L_{\rm M}\hspace{0.01cm}' > L_{\rm M}$. |
{Welcher Code könnte überhaupt ein Huffman–Code sein? | {Welcher Code könnte überhaupt ein Huffman–Code sein? | ||
|type="[]"} | |type="[]"} | ||
| − | + Code 1, | + | + $\text{Code 1}$, |
| − | - Code 2, | + | - $\text{Code 2}$, |
| − | - Code 3. | + | - $\text{Code 3}$. |
| Zeile 62: | Zeile 77: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
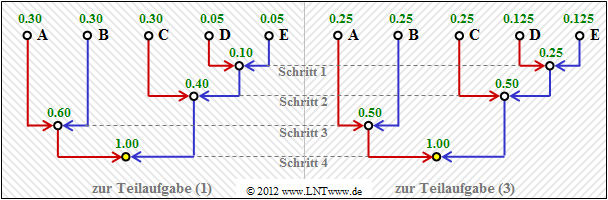
| − | + | [[Datei:Inf_Z_2_6a_version2.png|right|frame|Huffman–Baumdiagramme zu den Teilaufgaben '''(1)''' und '''(3)''']] | |
| − | + | '''(1)''' Richtig ist der <u>Lösungsvorschlag 1</u>. | |
| − | Die linke Grafik gilt für die Wahrscheinlichkeiten gemäß Teilaufgabe ( | + | *Die Grafik zeigt die Konstruktion des Huffman–Codes mittels Baumdiagramm. |
| + | *Mit der Zuordnung rot → <b>1</b> und blau → <b>0</b> erhält man: <br>$\rm A$ → <b>11</b>, $\rm B$ → <b>10</b>, $\rm C$ → <b>01</b>, $\rm D$ → <b>001</b>, $\rm E$ → <b>000</b>. | ||
| + | *Die linke Grafik gilt für die Wahrscheinlichkeiten gemäß Teilaufgabe '''(1)'''. | ||
| + | *Das rechte Diagramm gehört zur Teilaufgabe '''(3)''' mit etwas anderen Wahrscheinlichkeiten. | ||
| + | *Es liefert aber genau den gleichen Code. | ||
| + | <br clear=all> | ||
| + | '''(2)''' Richtig ist der <u>Lösungsvorschlag 3</u>, wie auch die folgende Rechnung zeigt: | ||
| + | :$$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (0.3 + 0.3 + 0.3) \cdot 2 + (0.05 + 0.05) \cdot 3 = 2.1\,{\rm bit/Quellensymbol}\hspace{0.05cm},$$ | ||
| + | :$$H \hspace{0.2cm} = \hspace{0.2cm} 3 \cdot 0.3 \cdot {\rm log_2}\hspace{0.15cm}(1/0.3) + 2 \cdot 0.05 \cdot {\rm log_2}\hspace{0.15cm}(1/0.05) | ||
| + | \approx 2.0\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Nach dem Quellencodierungstheorem gilt stets $L_{\rm M} \ge H$. | ||
| + | *Voraussetzung für $L_{\rm M} = H$ ist allerdings, dass alle Symbolwahrscheinlichkeiten in der Form $2^{-k} \ (k = 1, \ 2, \ 3,\ \text{ ...})$ dargestellt werden können. | ||
| + | *Dies trifft hier nicht zu. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(3)''' $\rm A$, $\rm B$ und $\rm C$ werden beim $\text{Code 1}$ durch zwei Bit dargestellt, $\rm E$ und $\rm F$ durch drei Bit. Damit erhält man für | |
| − | + | * die mittlere Codewortlänge | |
:$$L_{\rm M} = p_{\rm A}\cdot 2 + p_{\rm B}\cdot 2 + p_{\rm C}\cdot 2 + p_{\rm D}\cdot 3 + p_{\rm E}\cdot 3 | :$$L_{\rm M} = p_{\rm A}\cdot 2 + p_{\rm B}\cdot 2 + p_{\rm C}\cdot 2 + p_{\rm D}\cdot 3 + p_{\rm E}\cdot 3 | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | + | * für die Quellenentropie: | |
| − | :$$H = p_{\rm A}\cdot {\rm | + | :$$H = p_{\rm A}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm A}} + p_{\rm B}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm B}} + p_{\rm C}\cdot |
| − | {\rm | + | {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm C}} + p_{\rm D}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm D}} + p_{\rm E}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm E}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Durch Vergleich aller Terme kommt man zum Ergebnis: | Durch Vergleich aller Terme kommt man zum Ergebnis: | ||
| − | :$$p_{\rm A}= p_{\rm B}= p_{\rm C}\hspace{0.15cm}\underline{= 0.25} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm D}= p_{\rm E}\hspace{0.15cm}\underline{= 0.125} | + | :$$p_{\rm A}= p_{\rm B}= p_{\rm C}\hspace{0.15cm}\underline{= 0.25} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm D}= p_{\rm E}\hspace{0.15cm}\underline{= 0.125}\hspace{0.3cm} |
| − | + | \Rightarrow\hspace{0.3cm} L_{\rm M} = H = 2.25\,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$ | |
| − | Man erkennt: Mit diesen „günstigeren” Wahrscheinlichkeiten ergibt sich sogar eine größere mittlere Codewortlänge. Die Gleichheit ( | + | Man erkennt: |
| + | *Mit diesen „günstigeren” Wahrscheinlichkeiten ergibt sich sogar eine größere mittlere Codewortlänge als mit den „ungünstigeren”. | ||
| + | *Die Gleichheit $(L_{\rm M} = H)$ ist demzufolge allein auf die nun größere Quellenentropie zurückzuführen. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Beispielsweise liefert eine (von vielen) Simulationen mit den Wahrscheinlichkeiten gemäß der Teilaufgabe '''(3)''' die Folge mit $N = 40$ Zeichen: | ||
| + | :$$\rm EBDCCBDABEBABCCCCCBCAABECAACCBAABBBCDCAB.$$ | ||
| + | |||
| + | *Es ergibt sich $L_{\rm M}\hspace{0.01cm}' = ( 34 \cdot 2 + 6 \cdot 3)/50 = 2.15$ bit/Quellensymbol, also ein kleinerer Wert als für die unbegrenzte Folge $(L_{\rm M} = 2.25$ bit/Quellensymbol$)$. | ||
| + | *Bei anderem Startwert des Zufallsgenerators ist aber auch $(L_{\rm M}\hspace{0.03cm}' \ge L_{\rm M})$ möglich. | ||
| + | *Das heißt: <u>Alle Aussagen</u> sind zutreffend. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | :* Code 1 ist ein Huffman–Code, wie schon in den vorherigen Teilaufgaben gezeigt wurde. Dies gilt zwar nicht für alle Symbolwahrscheinlichkeiten, aber zumindest für die Parametersätze gemäß den Teilaufgaben ( | + | '''(5)''' Richtig ist nur der <u>Lösungsvorschlag 1</u>: |
| + | * Der $\text{Code 1}$ ist ein Huffman–Code, wie schon in den vorherigen Teilaufgaben gezeigt wurde. <br>Dies gilt zwar nicht für alle Symbolwahrscheinlichkeiten, aber zumindest für die Parametersätze gemäß den Teilaufgaben '''(1)''' und '''(3)'''. | ||
| − | + | * Der $\text{Code 2}$ ist kein Huffman–Code, da ein solcher stets präfixfrei sein müsste. <br>Die Präfixfreiheit ist hier aber nicht gegeben, da <b>1</b> der Beginn des Codewortes <b>10</b> ist. | |
| − | + | * Der $\text{Code 3}$ ist ebenfalls kein Huffman–Code, da er eine um $p_{\rm C}$ größere mittlere Codewortlänge aufweist als erforderlich $($siehe $\text{Code 1})$. Er ist nicht optimal. <br>Es gibt keine Symbolwahrscheinlichkeiten $p_{\rm A}$, ... , $p_{\rm E}$, die es rechtfertigen würden, das Symbol $\rm C$ mit <b>010</b> anstelle von <b>01</b> zu codieren. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Informationstheorie | + | [[Category:Aufgaben zu Informationstheorie|^2.3 Entropiecodierung nach Huffman^]] |
Aktuelle Version vom 10. August 2021, 15:48 Uhr
Der Algorithmus von David Albert Huffman realisiert eine Entropiecodierung mit folgenden Eigenschaften:
- Der entstehende Binärcode ist präfixfrei und somit in einfacher Weise (und sofort) decodierbar.
- Der Code führt bei gedächtnisloser Quelle zur kleinstmöglichen mittleren Codewortlänge $L_{\rm M}$.
- $L_{\rm M}$ ist aber nie kleiner als die Quellenentropie $H$.
- Diese beiden Größen sind allein aus den $M$ Symbolwahrscheinlichkeiten berechenbar.
Vorausgesetzt wird für diese Aufgabe eine gedächtnislose Quelle mit dem Symbolumfang $M = 5$ und dem Alphabet
- $$\{ {\rm A},\ {\rm B},\ {\rm C},\ {\rm D},\ {\rm E} \}.$$
In obiger Grafik sind drei Codes vorgegeben. Sie sollen entscheiden, welche dieser Codes durch Anwendung des Huffman–Algorithmus entstanden sind (oder sein könnten).
Hinweise:
- Die Aufgabe gehört zum Kapitel Entropiecodierung nach Huffman.
- Weitere Informationen zum Huffman–Algorithmus finden Sie auch im Angabenblatt zur Aufgabe 2.6.
- Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das Interaktionsmodul: Huffman- und Shannon-Fano-Codierung ⇒ $\text{SWF}$–Version.
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 1.
- Die Grafik zeigt die Konstruktion des Huffman–Codes mittels Baumdiagramm.
- Mit der Zuordnung rot → 1 und blau → 0 erhält man:
$\rm A$ → 11, $\rm B$ → 10, $\rm C$ → 01, $\rm D$ → 001, $\rm E$ → 000. - Die linke Grafik gilt für die Wahrscheinlichkeiten gemäß Teilaufgabe (1).
- Das rechte Diagramm gehört zur Teilaufgabe (3) mit etwas anderen Wahrscheinlichkeiten.
- Es liefert aber genau den gleichen Code.
(2) Richtig ist der Lösungsvorschlag 3, wie auch die folgende Rechnung zeigt:
- $$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (0.3 + 0.3 + 0.3) \cdot 2 + (0.05 + 0.05) \cdot 3 = 2.1\,{\rm bit/Quellensymbol}\hspace{0.05cm},$$
- $$H \hspace{0.2cm} = \hspace{0.2cm} 3 \cdot 0.3 \cdot {\rm log_2}\hspace{0.15cm}(1/0.3) + 2 \cdot 0.05 \cdot {\rm log_2}\hspace{0.15cm}(1/0.05) \approx 2.0\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
- Nach dem Quellencodierungstheorem gilt stets $L_{\rm M} \ge H$.
- Voraussetzung für $L_{\rm M} = H$ ist allerdings, dass alle Symbolwahrscheinlichkeiten in der Form $2^{-k} \ (k = 1, \ 2, \ 3,\ \text{ ...})$ dargestellt werden können.
- Dies trifft hier nicht zu.
(3) $\rm A$, $\rm B$ und $\rm C$ werden beim $\text{Code 1}$ durch zwei Bit dargestellt, $\rm E$ und $\rm F$ durch drei Bit. Damit erhält man für
- die mittlere Codewortlänge
- $$L_{\rm M} = p_{\rm A}\cdot 2 + p_{\rm B}\cdot 2 + p_{\rm C}\cdot 2 + p_{\rm D}\cdot 3 + p_{\rm E}\cdot 3 \hspace{0.05cm},$$
- für die Quellenentropie:
- $$H = p_{\rm A}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm A}} + p_{\rm B}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm B}} + p_{\rm C}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm C}} + p_{\rm D}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm D}} + p_{\rm E}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm E}} \hspace{0.05cm}.$$
Durch Vergleich aller Terme kommt man zum Ergebnis:
- $$p_{\rm A}= p_{\rm B}= p_{\rm C}\hspace{0.15cm}\underline{= 0.25} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm D}= p_{\rm E}\hspace{0.15cm}\underline{= 0.125}\hspace{0.3cm} \Rightarrow\hspace{0.3cm} L_{\rm M} = H = 2.25\,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Man erkennt:
- Mit diesen „günstigeren” Wahrscheinlichkeiten ergibt sich sogar eine größere mittlere Codewortlänge als mit den „ungünstigeren”.
- Die Gleichheit $(L_{\rm M} = H)$ ist demzufolge allein auf die nun größere Quellenentropie zurückzuführen.
(4) Beispielsweise liefert eine (von vielen) Simulationen mit den Wahrscheinlichkeiten gemäß der Teilaufgabe (3) die Folge mit $N = 40$ Zeichen:
- $$\rm EBDCCBDABEBABCCCCCBCAABECAACCBAABBBCDCAB.$$
- Es ergibt sich $L_{\rm M}\hspace{0.01cm}' = ( 34 \cdot 2 + 6 \cdot 3)/50 = 2.15$ bit/Quellensymbol, also ein kleinerer Wert als für die unbegrenzte Folge $(L_{\rm M} = 2.25$ bit/Quellensymbol$)$.
- Bei anderem Startwert des Zufallsgenerators ist aber auch $(L_{\rm M}\hspace{0.03cm}' \ge L_{\rm M})$ möglich.
- Das heißt: Alle Aussagen sind zutreffend.
(5) Richtig ist nur der Lösungsvorschlag 1:
- Der $\text{Code 1}$ ist ein Huffman–Code, wie schon in den vorherigen Teilaufgaben gezeigt wurde.
Dies gilt zwar nicht für alle Symbolwahrscheinlichkeiten, aber zumindest für die Parametersätze gemäß den Teilaufgaben (1) und (3).
- Der $\text{Code 2}$ ist kein Huffman–Code, da ein solcher stets präfixfrei sein müsste.
Die Präfixfreiheit ist hier aber nicht gegeben, da 1 der Beginn des Codewortes 10 ist.
- Der $\text{Code 3}$ ist ebenfalls kein Huffman–Code, da er eine um $p_{\rm C}$ größere mittlere Codewortlänge aufweist als erforderlich $($siehe $\text{Code 1})$. Er ist nicht optimal.
Es gibt keine Symbolwahrscheinlichkeiten $p_{\rm A}$, ... , $p_{\rm E}$, die es rechtfertigen würden, das Symbol $\rm C$ mit 010 anstelle von 01 zu codieren.