Aufgaben:Aufgabe 4.1: WDF, VTF und Wahrscheinlichkeit: Unterschied zwischen den Versionen
Khalil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Differentielle Entropie }} right| Zur Wiederholung einiger wichtiger Grundl…“) |
|||
| (19 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2862__Inf_A_4_1_neu.png|right|]] | + | [[Datei:P_ID2862__Inf_A_4_1_neu.png|right|frame|VTF (oben) und WDF (unten)]] |
| − | Zur Wiederholung einiger wichtiger Grundlagen aus dem Buch | + | Zur Wiederholung einiger wichtiger Grundlagen aus dem Buch „Stochastische Signaltheorie” |
beschäftigen wir uns mit | beschäftigen wir uns mit | ||
| − | + | * der [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsdichtefunktion]] (WDF), | |
| − | + | * der [[Stochastische_Signaltheorie/Verteilungsfunktion|Verteilungsfunktion]] (VTF). | |
| − | |||
| − | |||
| − | |||
| − | stellt zwei Möglichkeiten dar, um die Wahrscheinlichkeit für das Ereignis „Die Zufallsgröße | + | |
| + | Die obere Darstellung zeigt die Verteilungsfunktion $F_X(x)$ einer wertdiskreten Zufallsgröße $X$. Die zugehörige WDF $f_X(x)$ ist in der Teilaufgabe '''(1)''' zu bestimmen. | ||
| + | |||
| + | Die Gleichung | ||
| + | :$$ {\rm Pr}(A < X \le B) = F_X(B) - F_X(A) = \lim_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} \int_{A+\varepsilon}^{B+\varepsilon} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x $$ | ||
| + | |||
| + | stellt zwei Möglichkeiten dar, um aus der VTF bzw. der WDF die Wahrscheinlichkeit für das Ereignis „Die Zufallsgröße $X$ liegt in einem vorgegebenem Intervall” zu berechnen. | ||
Die untere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion | Die untere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion | ||
| − | $$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ | + | :$$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ |
y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$ | y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$ | ||
| − | einer wertkontinuierlichen Zufallsgröße Y, die auf den Bereich |'' | + | einer wertkontinuierlichen Zufallsgröße $Y$, die auf den Bereich $|Y| \le 2$ begrenzt ist. |
| + | |||
| + | Prinzipiell besteht bei der kontinuierlichen Zufallsgröße $Y$ der gleiche Zusammenhang zwischen WDF, VTF und den Wahrscheinlichkeiten wie bei einer diskreten Zufallsgröße. Sie werden trotzdem einige Detailunterschiede feststellen. | ||
| + | |||
| + | Beispielsweise kann bei der kontinuierlichen Zufallsgröße $Y$ in obiger Gleichung auf den Grenzübergang verzichtet werden, und man erhält vereinfacht: | ||
| + | :$${\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A) =\int_{A}^{B} \hspace{-0.01cm} f_Y(y) | ||
| + | \hspace{0.1cm}{\rm d}y\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Differentielle_Entropie|Differentielle Entropie]]. | ||
| + | *Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im dritten Kapitel „Kontinuierliche Zufallsgrößen” des Buches [[Stochastische Signaltheorie]]. | ||
| + | |||
| + | *Gegeben ist zudem das folgende unbstimmte Integral: | ||
| + | :$$\int \hspace{0.1cm} \cos^2(A \eta) \hspace{0.1cm}{\rm d}\eta = \frac{\eta}{2} + \frac{1}{4A} \cdot \sin(2A \eta).$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Bestimmen Sie die WDF | + | {Bestimmen Sie die WDF $f_X(x)$ der wertdiskreten Zufallsgröße $X$. Welche der folgenden Aussagen sind zutreffend? |
|type="[]"} | |type="[]"} | ||
+ Die WDF setzt sich aus fünf Diracfunktionen zusammen. | + Die WDF setzt sich aus fünf Diracfunktionen zusammen. | ||
| − | + Es gilt Pr( | + | + Es gilt ${\rm Pr}(X= 0) = 0.4$ und ${\rm Pr}(X= 1) = 0.2$. |
| − | - Es gilt Pr( | + | - Es gilt ${\rm Pr}(X= 2) = 0.4$. |
{Berechnen Sie die folgenden Wahrscheinlichkeiten: | {Berechnen Sie die folgenden Wahrscheinlichkeiten: | ||
|type="{}"} | |type="{}"} | ||
| − | $Pr(X > 0)$ | + | ${\rm Pr}(X > 0) \ = \ $ { 0.3 3% } |
| − | $Pr(|X| ≤ 1)$ | + | ${\rm Pr}(|X| ≤ 1) \ = \ $ { 0.8 3% } |
| − | {Welche Werte ergeben sich für die Verteilungsfunktion | + | {Welche Werte ergeben sich für die Verteilungsfunktion $F_Y(y) ={\rm Pr}(Y \le y)$ der wertkontinuierlichen Zufallsgröße $Y$, insbesondere: |
|type="{}"} | |type="{}"} | ||
| − | $F_Y(y = 0)$ | + | $F_Y(y = 0) \ = \ $ { 0.5 3% } |
| − | $F_Y(y = 1)$ | + | $F_Y(y = 1) \ = \ $ { 0.909 3% } |
| − | $F_Y(y = 2)$ | + | $F_Y(y = 2) \ = \ $ { 1 3% } |
| − | {Wie groß ist die Wahrscheinlichkeit, dass | + | {Wie groß ist die Wahrscheinlichkeit, dass $Y = 0$ ist? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(Y = 0)$ | + | ${\rm Pr}(Y = 0) \ = \ $ { 0. } |
{Welche der folgenden Aussagen sind richtig? | {Welche der folgenden Aussagen sind richtig? | ||
|type="[]"} | |type="[]"} | ||
| − | - Das Ergebnis | + | - Das Ergebnis $Y = 0$ ist unmöglich. |
| − | + Das Ergebnis | + | + Das Ergebnis $Y = 3$ ist unmöglich. |
{Wie groß sind die folgenden Wahrscheinlichkeiten? | {Wie groß sind die folgenden Wahrscheinlichkeiten? | ||
|type="{}"} | |type="{}"} | ||
| − | $Pr(Y > 0)$ | + | ${\rm Pr}(Y > 0) \ = \ $ { 0.5 3% } |
| − | $Pr(|Y| ≤ 1)$ | + | ${\rm Pr}(|Y| ≤ 1) \ = \ $ { 0.818 3% } |
</quiz> | </quiz> | ||
| Zeile 66: | Zeile 84: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[Datei:P_ID2857__Inf_A_4_1a_neu.png|right|]] | + | [[Datei:P_ID2857__Inf_A_4_1a_neu.png|right|frame|WDF und VTF der <br>diskreten Zufallsgröße $X$]] |
| − | < | + | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 2</u>: |
| − | Die vorgegebene VTF beinhaltet fünf Unstetigkeitsstellen, die nach der Differentiation zu fünf Diracfunktionen führen: | + | *Die Verteilungsfunktion (VTF) $F_X(x)$ ergibt sich aus der Wahrscheinlichkeitsdichtefunktion $f_X(x)$ durch Integration über die (umbenannte) Zufallsgröße im Bereich von $- \infty$ bis $x$. |
| − | $$f_X(x) | + | *Die Umkehrung lautet: Ist die VTF gegeben, so erhält man die WDF durch Differentiation. |
| − | + 0.2 \cdot {\rm \delta}( x+1) | + | *Die vorgegebene VTF beinhaltet fünf Unstetigkeitsstellen, die nach der Differentiation zu fünf Diracfunktionen führen: |
| − | + | + | :$$f_X(x) = 0.1 \cdot {\rm \delta}( x+2) |
| − | + | + | + 0.2 \cdot {\rm \delta}( x+1) |
| − | Die Diracgewichte geben die Auftrittswahrscheinlichkeiten der Zufallsgröße | + | + 0.4 \cdot {\rm \delta}( x) + 0.2 \cdot {\rm \delta}( x-1) |
| − | $${\rm Pr}(X = 0) | + | + 0.1 \cdot {\rm \delta}( x-2)\hspace{0.05cm}.$$ |
| − | + | *Die Diracgewichte geben die Auftrittswahrscheinlichkeiten der Zufallsgröße $X = \{-2,\ -1,\ 0,\ +1,\ +2\}$ an, <br>zum Beispiel: | |
| − | Dementsprechend lauten die weiteren Wahrscheinlichkeiten: | + | :$${\rm Pr}(X = 0) = F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-}) = |
| − | $${\rm Pr}(X = +1) = {\rm Pr}(X = -1) = 0.2\hspace{0.05cm},\hspace{0.3cm} | + | 0.7 - 0.3 = 0.4\hspace{0.05cm}.$$ |
| + | *Dementsprechend lauten die weiteren Wahrscheinlichkeiten: | ||
| + | :$${\rm Pr}(X = +1) = {\rm Pr}(X = -1) = 0.2\hspace{0.05cm},\hspace{0.3cm} | ||
{\rm Pr}(X = +2) = {\rm Pr}(X = -2) = 0.1\hspace{0.05cm}.$$ | {\rm Pr}(X = +2) = {\rm Pr}(X = -2) = 0.1\hspace{0.05cm}.$$ | ||
| − | |||
| − | + | ||
| − | $${\rm Pr}(X >0) | + | |
| − | \hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$ $$ | + | '''(2)''' Aus der eben berechneten WDF erhält man: |
| − | {\rm Pr}(|X| \le 1) | + | :$${\rm Pr}(X >0) = {\rm Pr}(X = +1) + {\rm Pr}(X = +2) |
| − | {\rm Pr}(X = -1) + {\rm Pr}(X = 0) + {\rm Pr}(X = +1) = 0.2 + 0.4 +0.2 | + | \hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$ |
| + | :$${\rm Pr}(|X| \le 1) ={\rm Pr}(X = -1) + {\rm Pr}(X = 0) + {\rm Pr}(X = +1) = 0.2 + 0.4 +0.2 | ||
\hspace{0.15cm}\underline {= 0.8}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline {= 0.8}\hspace{0.05cm}.$$ | ||
| − | Zum gleichen Ergebnis kommt man über die Verteilungsfunktion. Hier lautet die allgemeine Gleichung, die für wertdiskrete und wertkontinuierliche Zufallsgrößen gleichermaßen gilt: | + | Zum gleichen Ergebnis kommt man über die Verteilungsfunktion. Hier lautet die allgemeine Gleichung, die für wertdiskrete und wertkontinuierliche Zufallsgrößen gleichermaßen gilt: |
| − | $${\rm Pr}(A < X \le B) =F_X(B) - F_X(A) \hspace{0.05cm}.$$ | + | :$${\rm Pr}(A < X \le B) =F_X(B) - F_X(A) \hspace{0.05cm}.$$ |
| + | |||
| + | * Mit $A= 0$ und $B = +2$ erhält man somit: | ||
| + | :$${\rm Pr}(0 < X \le +2) = {\rm Pr}(X >0)= F_X(+2) - F_X(0) = 1 - 0.7 \hspace{0.15cm}\underline {= 0.3} \hspace{0.05cm}.$$ | ||
| + | *Setzt man $A=-2$ und $B = +1$, so ergibt sich: | ||
| + | :$${\rm Pr}(-2 < X \le +1) = {\rm Pr}(|X| \le 1)= F_X(+1) - F_X(-2) = 0.9 - 0.1 \hspace{0.15cm}\underline {= 0.8} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Datei:P_ID2858__Inf_A_4_1c_neu.png|right|frame|WDF und VTF der kontinuierlichen Zufallsgröße $Y$]] | |
| − | $${\rm | + | '''(3)''' Die Verteilungsfunktion $F_Y(y)$ ergibt sich aus der (umbenannten) WDF $f_Y(\eta)$ durch Integration von $- \infty$ bis $x$. Aufgrund der Symmetrie kann hierfür im Bereich $0 \le y \le +2$ geschrieben werden: |
| + | :$$F_Y(y) = \int_{-\infty}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta ={1}/{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}F_Y(y) = \frac{1}{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{0.1cm}\frac{1}{2} \cdot \cos^2({\pi}/{4} \cdot \eta) \hspace{0.1cm}{\rm d}\eta = \frac{1}{2}+\frac{y}{4} + \frac{1}{2\pi} \cdot \sin({\pi}/{2} \cdot y).$$ | ||
| + | Die Gleichung gilt im gesamten Bereich $0 \le y \le +2$. Die gesuchten VTF–Werte sind damit: | ||
| + | *$F_Y(y=0)\hspace{0.15cm}\underline{= 0.5}$ (Integral über die halbe WDF), | ||
| + | *$F_Y(y=1)= 3/4 + 1/(2 \pi)\hspace{0.15cm}\underline{= 0.909}$ (rot hinterlegte Fläche in der WDF), | ||
| + | *$F_Y(y=2)\hspace{0.15cm}\underline{= 1}$ (Integral über die gesamte WDF). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' Die Wahrscheinlichkeit, dass die wertkontinuierliche Zufallsgröße $Y$ im Bereich von $-\varepsilon$ bis $+\varepsilon$ liegt, kann mit der angegebenen Gleichung wie folgt berechnet werden: | |
| + | :$${\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = F_Y(+\varepsilon) - F_Y(-\varepsilon) \hspace{0.05cm}.$$ | ||
| − | + | *Berücksichtigt wurde, dass man bei der kontinuierlichen Zufallsgröße $Y$ das „<”–Zeichen ohne Verfälschung durch das „≤”–Zeichen ersetzen kann. | |
| − | + | *Mit dem Grenzübergang $\varepsilon \to 0$ ergibt sich die gesuchte Wahrscheinlichkeit: | |
| + | :$${\rm Pr}(Y = 0) =\lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm}{\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = | ||
| + | \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(+\varepsilon) - \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(-\varepsilon) = | ||
| + | F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-})\hspace{0.05cm}.$$ | ||
| − | + | *Da bei einer kontinuierlichen Zufallsgröße die beiden Grenzwerte gleich sind, gilt $\underline{{\rm Pr}(Y = 0) = 0}$. | |
| − | $${\rm Pr}( Y > 0) = {\rm Pr}(0 \le Y \le \infty) | + | |
| + | |||
| + | '''Allgemein gilt''': Die Wahrscheinlichkeit ${\rm Pr}(Y = y_0)$, dass eine wertkontinuierliche Zufallsgröße $Y$ einen festen Wert $y_0$ annimmt, ist stets Null. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | ||
| + | *Aufgrund der vorliegenden WDF kann das Ergebnis $Y=3$ ausgeschlossen werden. | ||
| + | *Das Ergebnis $Y=0$ ist dagegen durchaus möglich, obwohl ${\rm Pr}(Y = 0) = 0$ ist. | ||
| + | *Führt man zum Beispiel ein Zufallsexperiment $N \to \infty$ mal durch und erhält dabei $N_0$ mal das Ergebnis $Y= 0$, so gilt bei endlichem $N_0$ nach der klassischen Definition der Wahrscheinlichkeit: | ||
| + | :$${\rm Pr}(Y = 0) = \lim_{N\hspace{0.05cm}\rightarrow\hspace{0.05cm}\infty}\hspace{0.1cm}{N_0}/{N} = 0\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Wir gehen wieder von der von der für die kontinuierliche Zufallsgröße $Y$ gültigen Gleichung $ {\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A)$ aus: | ||
| + | *Mit $A = 0$ und $B \to \infty$ $($bzw. $B = 2)$ erhält man: | ||
| + | :$${\rm Pr}( Y > 0) = {\rm Pr}(0 \le Y \le \infty) | ||
= {\rm Pr}(0 \le Y \le 2) = F_Y(2) - F_Y(0) | = {\rm Pr}(0 \le Y \le 2) = F_Y(2) - F_Y(0) | ||
\hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}.$$ | ||
| − | + | *Bei der symmetrischen kontinuierlichen Zufallsgröße $Y$ ist also tatsächlich erwartungsgemäß ${\rm Pr}( Y > 0) = 1/2$. | |
| − | Bei der symmetrischen kontinuierlichen Zufallsgröße | + | *Obwohl auch die wertdiskrete Zufallsgröße $X$ symmetrisch um $x= 0$ ist, wurde in der Teilaufgabe '''(3)''' dagegen ${\rm Pr}( X > 0) = 0.3$ ermittelt. |
| − | + | *Weiter erhält man mit $A = -1$ und $B = +1$ wegen $F_Y(-1) = 1- F_Y(+1)$: | |
| − | + | :$${\rm Pr}( |Y| \le 1) = {\rm Pr}(-1 \le Y \le +1) | |
| − | $${\rm Pr}( |Y| \le 1) = {\rm Pr}(-1 \le Y \le +1) | + | = F_Y(+1) - F_Y(-1) = 2 \cdot F_Y(+1) -1 = 2 \cdot 0.909 -1 \hspace{0.15cm}\underline {= 0.818}. $$ |
| − | = F_Y(+1) - F_Y(-1) | ||
| − | = 2 \cdot F_Y(+1) -1 = 2 \cdot 0.909 -1 \hspace{0.15cm}\underline {= 0.818}. $$ | ||
Aktuelle Version vom 24. September 2021, 13:40 Uhr
Zur Wiederholung einiger wichtiger Grundlagen aus dem Buch „Stochastische Signaltheorie” beschäftigen wir uns mit
- der Wahrscheinlichkeitsdichtefunktion (WDF),
- der Verteilungsfunktion (VTF).
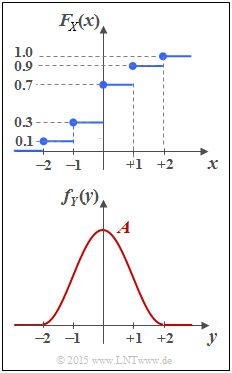
Die obere Darstellung zeigt die Verteilungsfunktion $F_X(x)$ einer wertdiskreten Zufallsgröße $X$. Die zugehörige WDF $f_X(x)$ ist in der Teilaufgabe (1) zu bestimmen.
Die Gleichung
- $$ {\rm Pr}(A < X \le B) = F_X(B) - F_X(A) = \lim_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} \int_{A+\varepsilon}^{B+\varepsilon} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x $$
stellt zwei Möglichkeiten dar, um aus der VTF bzw. der WDF die Wahrscheinlichkeit für das Ereignis „Die Zufallsgröße $X$ liegt in einem vorgegebenem Intervall” zu berechnen.
Die untere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion
- $$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$
einer wertkontinuierlichen Zufallsgröße $Y$, die auf den Bereich $|Y| \le 2$ begrenzt ist.
Prinzipiell besteht bei der kontinuierlichen Zufallsgröße $Y$ der gleiche Zusammenhang zwischen WDF, VTF und den Wahrscheinlichkeiten wie bei einer diskreten Zufallsgröße. Sie werden trotzdem einige Detailunterschiede feststellen.
Beispielsweise kann bei der kontinuierlichen Zufallsgröße $Y$ in obiger Gleichung auf den Grenzübergang verzichtet werden, und man erhält vereinfacht:
- $${\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A) =\int_{A}^{B} \hspace{-0.01cm} f_Y(y) \hspace{0.1cm}{\rm d}y\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Differentielle Entropie.
- Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im dritten Kapitel „Kontinuierliche Zufallsgrößen” des Buches Stochastische Signaltheorie.
- Gegeben ist zudem das folgende unbstimmte Integral:
- $$\int \hspace{0.1cm} \cos^2(A \eta) \hspace{0.1cm}{\rm d}\eta = \frac{\eta}{2} + \frac{1}{4A} \cdot \sin(2A \eta).$$
Fragebogen
Musterlösung
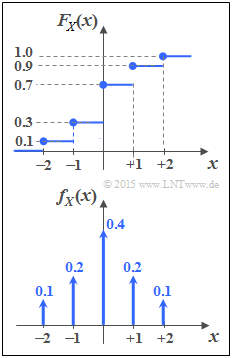
(1) Richtig sind die Lösungsvorschläge 1 und 2:
- Die Verteilungsfunktion (VTF) $F_X(x)$ ergibt sich aus der Wahrscheinlichkeitsdichtefunktion $f_X(x)$ durch Integration über die (umbenannte) Zufallsgröße im Bereich von $- \infty$ bis $x$.
- Die Umkehrung lautet: Ist die VTF gegeben, so erhält man die WDF durch Differentiation.
- Die vorgegebene VTF beinhaltet fünf Unstetigkeitsstellen, die nach der Differentiation zu fünf Diracfunktionen führen:
- $$f_X(x) = 0.1 \cdot {\rm \delta}( x+2) + 0.2 \cdot {\rm \delta}( x+1) + 0.4 \cdot {\rm \delta}( x) + 0.2 \cdot {\rm \delta}( x-1) + 0.1 \cdot {\rm \delta}( x-2)\hspace{0.05cm}.$$
- Die Diracgewichte geben die Auftrittswahrscheinlichkeiten der Zufallsgröße $X = \{-2,\ -1,\ 0,\ +1,\ +2\}$ an,
zum Beispiel:
- $${\rm Pr}(X = 0) = F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-}) = 0.7 - 0.3 = 0.4\hspace{0.05cm}.$$
- Dementsprechend lauten die weiteren Wahrscheinlichkeiten:
- $${\rm Pr}(X = +1) = {\rm Pr}(X = -1) = 0.2\hspace{0.05cm},\hspace{0.3cm} {\rm Pr}(X = +2) = {\rm Pr}(X = -2) = 0.1\hspace{0.05cm}.$$
(2) Aus der eben berechneten WDF erhält man:
- $${\rm Pr}(X >0) = {\rm Pr}(X = +1) + {\rm Pr}(X = +2) \hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$
- $${\rm Pr}(|X| \le 1) ={\rm Pr}(X = -1) + {\rm Pr}(X = 0) + {\rm Pr}(X = +1) = 0.2 + 0.4 +0.2 \hspace{0.15cm}\underline {= 0.8}\hspace{0.05cm}.$$
Zum gleichen Ergebnis kommt man über die Verteilungsfunktion. Hier lautet die allgemeine Gleichung, die für wertdiskrete und wertkontinuierliche Zufallsgrößen gleichermaßen gilt:
- $${\rm Pr}(A < X \le B) =F_X(B) - F_X(A) \hspace{0.05cm}.$$
- Mit $A= 0$ und $B = +2$ erhält man somit:
- $${\rm Pr}(0 < X \le +2) = {\rm Pr}(X >0)= F_X(+2) - F_X(0) = 1 - 0.7 \hspace{0.15cm}\underline {= 0.3} \hspace{0.05cm}.$$
- Setzt man $A=-2$ und $B = +1$, so ergibt sich:
- $${\rm Pr}(-2 < X \le +1) = {\rm Pr}(|X| \le 1)= F_X(+1) - F_X(-2) = 0.9 - 0.1 \hspace{0.15cm}\underline {= 0.8} \hspace{0.05cm}.$$
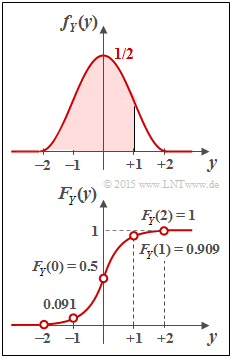
(3) Die Verteilungsfunktion $F_Y(y)$ ergibt sich aus der (umbenannten) WDF $f_Y(\eta)$ durch Integration von $- \infty$ bis $x$. Aufgrund der Symmetrie kann hierfür im Bereich $0 \le y \le +2$ geschrieben werden:
- $$F_Y(y) = \int_{-\infty}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta ={1}/{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta$$
- $$\Rightarrow \hspace{0.3cm}F_Y(y) = \frac{1}{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{0.1cm}\frac{1}{2} \cdot \cos^2({\pi}/{4} \cdot \eta) \hspace{0.1cm}{\rm d}\eta = \frac{1}{2}+\frac{y}{4} + \frac{1}{2\pi} \cdot \sin({\pi}/{2} \cdot y).$$
Die Gleichung gilt im gesamten Bereich $0 \le y \le +2$. Die gesuchten VTF–Werte sind damit:
- $F_Y(y=0)\hspace{0.15cm}\underline{= 0.5}$ (Integral über die halbe WDF),
- $F_Y(y=1)= 3/4 + 1/(2 \pi)\hspace{0.15cm}\underline{= 0.909}$ (rot hinterlegte Fläche in der WDF),
- $F_Y(y=2)\hspace{0.15cm}\underline{= 1}$ (Integral über die gesamte WDF).
(4) Die Wahrscheinlichkeit, dass die wertkontinuierliche Zufallsgröße $Y$ im Bereich von $-\varepsilon$ bis $+\varepsilon$ liegt, kann mit der angegebenen Gleichung wie folgt berechnet werden:
- $${\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = F_Y(+\varepsilon) - F_Y(-\varepsilon) \hspace{0.05cm}.$$
- Berücksichtigt wurde, dass man bei der kontinuierlichen Zufallsgröße $Y$ das „<”–Zeichen ohne Verfälschung durch das „≤”–Zeichen ersetzen kann.
- Mit dem Grenzübergang $\varepsilon \to 0$ ergibt sich die gesuchte Wahrscheinlichkeit:
- $${\rm Pr}(Y = 0) =\lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm}{\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(+\varepsilon) - \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(-\varepsilon) = F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-})\hspace{0.05cm}.$$
- Da bei einer kontinuierlichen Zufallsgröße die beiden Grenzwerte gleich sind, gilt $\underline{{\rm Pr}(Y = 0) = 0}$.
Allgemein gilt: Die Wahrscheinlichkeit ${\rm Pr}(Y = y_0)$, dass eine wertkontinuierliche Zufallsgröße $Y$ einen festen Wert $y_0$ annimmt, ist stets Null.
(5) Richtig ist der Lösungsvorschlag 2:
- Aufgrund der vorliegenden WDF kann das Ergebnis $Y=3$ ausgeschlossen werden.
- Das Ergebnis $Y=0$ ist dagegen durchaus möglich, obwohl ${\rm Pr}(Y = 0) = 0$ ist.
- Führt man zum Beispiel ein Zufallsexperiment $N \to \infty$ mal durch und erhält dabei $N_0$ mal das Ergebnis $Y= 0$, so gilt bei endlichem $N_0$ nach der klassischen Definition der Wahrscheinlichkeit:
- $${\rm Pr}(Y = 0) = \lim_{N\hspace{0.05cm}\rightarrow\hspace{0.05cm}\infty}\hspace{0.1cm}{N_0}/{N} = 0\hspace{0.05cm}.$$
(6) Wir gehen wieder von der von der für die kontinuierliche Zufallsgröße $Y$ gültigen Gleichung $ {\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A)$ aus:
- Mit $A = 0$ und $B \to \infty$ $($bzw. $B = 2)$ erhält man:
- $${\rm Pr}( Y > 0) = {\rm Pr}(0 \le Y \le \infty) = {\rm Pr}(0 \le Y \le 2) = F_Y(2) - F_Y(0) \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}.$$
- Bei der symmetrischen kontinuierlichen Zufallsgröße $Y$ ist also tatsächlich erwartungsgemäß ${\rm Pr}( Y > 0) = 1/2$.
- Obwohl auch die wertdiskrete Zufallsgröße $X$ symmetrisch um $x= 0$ ist, wurde in der Teilaufgabe (3) dagegen ${\rm Pr}( X > 0) = 0.3$ ermittelt.
- Weiter erhält man mit $A = -1$ und $B = +1$ wegen $F_Y(-1) = 1- F_Y(+1)$:
- $${\rm Pr}( |Y| \le 1) = {\rm Pr}(-1 \le Y \le +1) = F_Y(+1) - F_Y(-1) = 2 \cdot F_Y(+1) -1 = 2 \cdot 0.909 -1 \hspace{0.15cm}\underline {= 0.818}. $$