Aufgaben:Aufgabe 4.9: Höherstufige Modulation: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 6: | Zeile 6: | ||
Die Grafik zeigt AWGN–Kanalkapazitätskurven über der Abszisse $10 \cdot \lg (E_{\rm S}/{N_0})$: | Die Grafik zeigt AWGN–Kanalkapazitätskurven über der Abszisse $10 \cdot \lg (E_{\rm S}/{N_0})$: | ||
* $C_\text{Gauß}$: Shannonsche Grenzkurve, | * $C_\text{Gauß}$: Shannonsche Grenzkurve, | ||
| − | * $C_\text{BPSK}$: gültig für | + | * $C_\text{BPSK}$: gültig für "Binary Phase Shift Keying" $\rm (BPSK)$. |
| Zeile 15: | Zeile 15: | ||
| − | + | Hinweise: | |
| − | |||
| − | |||
*Die Aufgabe gehört zum Kapitel [[Informationstheorie/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang|AWGN–Kanalkapazität bei wertdiskretem Eingang]]. | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang|AWGN–Kanalkapazität bei wertdiskretem Eingang]]. | ||
| − | *Bezug genommen wird insbesondere auf die Seite [[Informationstheorie/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#Die_Kanalkapazit.C3.A4t_.7F.27.22.60UNIQ-MathJax82-QINU.60.22.27.7F_als_Funktion_von_.7F.27.22.60UNIQ-MathJax83-QINU.60.22.27.7F| | + | *Bezug genommen wird insbesondere auf die Seite [[Informationstheorie/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#Die_Kanalkapazit.C3.A4t_.7F.27.22.60UNIQ-MathJax82-QINU.60.22.27.7F_als_Funktion_von_.7F.27.22.60UNIQ-MathJax83-QINU.60.22.27.7F|Kanalkapazität $C$ als Funktion von $E_{\rm S}/{N_0}$]]. |
| − | *Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log” ⇒ „log<sub>2</sub>” verwendet. | + | *Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log” ⇒ „log<sub>2</sub>” verwendet. |
| − | *Die im Fragebogen genannten Modulationsverfahren werden anhand ihrer Signalraumkonstellation beschrieben | + | *Die im Fragebogen genannten Modulationsverfahren werden anhand ihrer Signalraumkonstellation beschrieben. |
| Zeile 27: | Zeile 25: | ||
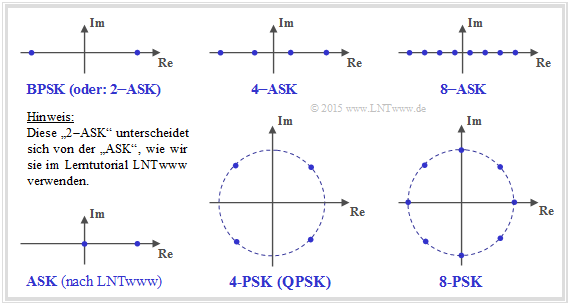
[[Datei:P_ID2953__Inf_A_4_9_Zusatz.png|right|frame|Vorgeschlagene Signalraumkonstellationen]] | [[Datei:P_ID2953__Inf_A_4_9_Zusatz.png|right|frame|Vorgeschlagene Signalraumkonstellationen]] | ||
| − | ''Anmerkungen zur Nomenklatur'': | + | '''Anmerkungen zur Nomenklatur''': |
| − | *In der Literatur wird manchmal die „BPSK” auch mit „2–ASK” bezeichnet | + | *In der Literatur wird manchmal die „BPSK” auch mit „2–ASK” bezeichnet: |
:$$x ∈ X = \{+1,\ -1\}.$$ | :$$x ∈ X = \{+1,\ -1\}.$$ | ||
| − | *Dagegen verstehen wir | + | *Dagegen verstehen wir hier als „ASK” den unipolaren Fall: |
:$$x ∈ X = \{0,\ 1 \}.$$ | :$$x ∈ X = \{0,\ 1 \}.$$ | ||
*Nach unserer Nomenklatur gilt deshalb: | *Nach unserer Nomenklatur gilt deshalb: | ||
| − | :$$C_\text{ | + | :$$C_\text{ASK} < C_\text{BPSK}.$$ |
| − | Dieser Sachverhalt ist unerheblich für die Lösung der vorliegenden Aufgabe. | + | :Dieser Sachverhalt ist allerdings unerheblich für die Lösung der vorliegenden Aufgabe. |
| Zeile 43: | Zeile 41: | ||
{Welche Gleichung liegt der Shannon–Grenzkurve $C_{\rm Gauß}$ zugrunde? | {Welche Gleichung liegt der Shannon–Grenzkurve $C_{\rm Gauß}$ zugrunde? | ||
|type="[]"} | |type="[]"} | ||
| − | - Es gilt $C_{\rm Gauß} = C_1= {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + E_{\rm S}/{N_0})$ , | + | - Es gilt $C_{\rm Gauß} = C_1= {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + E_{\rm S}/{N_0})$, |
| − | + Es gilt $C_{\rm Gauß} = C_2= {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot E_{\rm S}/{N_0})$ , | + | + Es gilt $C_{\rm Gauß} = C_2= {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot E_{\rm S}/{N_0})$, |
| − | - Es gilt $C_{\rm Gauß} = C_3= {\rm log}_2 \hspace{0.1cm} ( 1 + E_{\rm S}/{N_0})$ . | + | - Es gilt $C_{\rm Gauß} = C_3= {\rm log}_2 \hspace{0.1cm} ( 1 + E_{\rm S}/{N_0})$. |
| − | {Welche Aussagen treffen für die grüne | + | {Welche Aussagen treffen für die grüne $C_{\rm BPSK}$–Kurve zu? |
|type="[]"} | |type="[]"} | ||
+ $C_{\rm BPSK}$ kann nicht in geschlossener Form angegeben werden. | + $C_{\rm BPSK}$ kann nicht in geschlossener Form angegeben werden. | ||
| − | + $C_{\rm BPSK}$ ist größer als Null, wenn $E_{\rm S}/{N_0} > 0$ vorausgesetzt wird. | + | + $C_{\rm BPSK}$ ist größer als Null, wenn $E_{\rm S}/{N_0} > 0$ vorausgesetzt wird. |
- Für $E_{\rm S}/{N_0} < \ln (2)$ ist $C_{\rm BPSK} ≡ 0$. | - Für $E_{\rm S}/{N_0} < \ln (2)$ ist $C_{\rm BPSK} ≡ 0$. | ||
+ Im gesamten Bereich gilt $C_{\rm BPSK} < C_{\rm Gauß} $. | + Im gesamten Bereich gilt $C_{\rm BPSK} < C_{\rm Gauß} $. | ||
| Zeile 64: | Zeile 62: | ||
| − | {Welche Aussagen treffen für die braune Kurve $C_{\rm braun}$ zu? | + | {Welche Aussagen treffen für die braune Kurve $C_{\rm braun}$ zu? <br>Hinweis: $p_{\rm B}$ bezeichnet hierbei die Bitfehlerwahrscheinlichkeit. |
|type="[]"} | |type="[]"} | ||
+ Für die zugehörige Zufallsgröße $X$ gilt $M_X = |X| = 8$. | + Für die zugehörige Zufallsgröße $X$ gilt $M_X = |X| = 8$. | ||
Version vom 4. November 2021, 12:37 Uhr
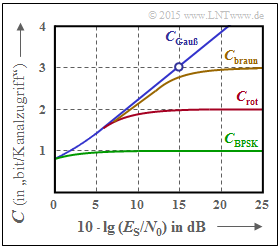
Die Grafik zeigt AWGN–Kanalkapazitätskurven über der Abszisse $10 \cdot \lg (E_{\rm S}/{N_0})$:
- $C_\text{Gauß}$: Shannonsche Grenzkurve,
- $C_\text{BPSK}$: gültig für "Binary Phase Shift Keying" $\rm (BPSK)$.
Die beiden weiteren Kurvenverläufe $C_\text{rot}$ und $C_\text{braun}$ sollen in den Teilaufgaben (3) und (4) analysiert und möglichen Modulationsverfahren zugeordnet werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertdiskretem Eingang.
- Bezug genommen wird insbesondere auf die Seite Kanalkapazität $C$ als Funktion von $E_{\rm S}/{N_0}$.
- Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log” ⇒ „log2” verwendet.
- Die im Fragebogen genannten Modulationsverfahren werden anhand ihrer Signalraumkonstellation beschrieben.
Anmerkungen zur Nomenklatur:
- In der Literatur wird manchmal die „BPSK” auch mit „2–ASK” bezeichnet:
- $$x ∈ X = \{+1,\ -1\}.$$
- Dagegen verstehen wir hier als „ASK” den unipolaren Fall:
- $$x ∈ X = \{0,\ 1 \}.$$
- Nach unserer Nomenklatur gilt deshalb:
- $$C_\text{ASK} < C_\text{BPSK}.$$
- Dieser Sachverhalt ist allerdings unerheblich für die Lösung der vorliegenden Aufgabe.
Fragebogen
Musterlösung
(1) Richtig ist der Vorschlag 2, wie die Rechnung für $10 \cdot \lg (E_{\rm S}/{N_0}) = 15 \ \rm dB$ ⇒ $E_{\rm S}/{N_0} = 31.62$ zeigt:
- $$C_2(15\hspace{0.1cm}{\rm dB}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot 31.62 ) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 64.25 ) \approx 3\,{\rm bit/Kanalzugriff}\hspace{0.05cm}. $$
- Die beiden anderen Lösungsvorschläge liefern folgende Zahlenwerte:
- $$C_3(15\hspace{0.1cm}{\rm dB}) \ = \ {\rm log}_2 \hspace{0.1cm} ( 1 + 31.62 ) \approx 5.03\,{\rm bit/Kanalzugriff}\hspace{0.05cm},$$
- $$ C_1(15\hspace{0.1cm}{\rm dB}) \ = \ C_3/2 \approx 2.51\,{\rm bit/Kanalzugriff}\hspace{0.05cm}.$$
- Der Lösungsvorschlag 3 entspricht dabei dem Fall Zweier unabhängiger Gaußkanäle mit jeweils halber Sendeleistung pro Kanal.
(2) Richtig sind die Lösungsvorschläge 1, 2 und 4:
- Würde man $E_{\rm S}$ durch $E_{\rm B}$ ersetzen, so wäre auch die Aussage 3 richtig.
- Für $E_{\rm B}/{N_0} < \ln (2)$ gilt nämlich $C_{\rm Gauß} ≡ 0$ und damit auch $C_{\rm BPSK} ≡ 0$ .
(3) Richtig sind die Aussagen 2, 3 und 5:
- Der rote Kurvenzug $C_{\rm rot}$ liegt stets oberhalb von $C_{\rm BPSK}$ , aber unterhalb von $C_{\rm braun}$ und der Shannon–Grenzkurve $C_{\rm Gauß}$.
- Die Aussagen gelten auch, wenn für gewisse $E_{\rm S}/{N_0}$–Werte Kurven innerhalb der Zeichengenauigkeit nicht zu unterscheiden sind.
- Aus dem Grenzwert $C_{\rm rot}= 2 \ \rm bit/Kanalzugriff$ für $E_{\rm S}/{N_0} → ∞$ ergibt sich der Symbolumfang $M_X = |X| = 4$.
- Die rote Kurve beschreibt also die 4–ASK. $M_X = |X| = 2$ würde für die BPSK gelten.
- Die 4–QAM führt genau zum gleichen Endwert „2 bit/Kanalzugriff”. Für kleine $E_{\rm S}/{N_0}$–Werte liegt aber die Kanalkapazität $C_{\rm 4–QAM}$ oberhalb der roten Kurve, da $C_{\rm rot}$ von der Gauß–Grenzkurve $C_2$ begrenzt wird, $C_{\rm 4–QAM}$ aber von $C_3$.
Die Bezeichnungen $C_2$ und $C_3$ beziehen sich hierbei auf die Teilaufgabe (1).
(4) Richtig sind die Lösungsvorschläge 1, 2 und 5:
- Aus dem braunen Kurvenverlauf erkennt man die Richtigkeit der beiden ersten Aussagen.
- Die 8–PSK mit I– und Q–Komponente – also mit $K = 2$ Dimensionen – liegt für kleine $E_{\rm S}/{N_0}$–Werte etwas oberhalb der braunen Kurve ⇒ die Antwort 3 ist falsch.
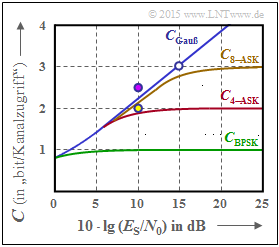
In der Grafik sind auch die beiden 8–ASK–Systeme gemäß den Vorschlägen 4 und 5 als Punkte eingezeichnet.
- Der violette Punkt liegt über der Kurve $C_{\rm 8–ASK}$ ⇒ $R = 2.5$ und $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ reichen nicht aus, um die 8–ASK fehlerfrei decodieren zu können ⇒ $R > C$ ⇒ das Kanalcodierungstheorem wird nicht erfüllt ⇒ Antwort 4 ist falsch.
- Reduziert man aber die Coderate gemäß dem gelben Punkt bei gleichem $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ auf $R = 2 < C_{\rm 8–ASK}$, so wird das Kanalcodierungstheorem erfüllt ⇒ Antwort 5 ist richtig.