Aufgaben:Aufgabe 4.1: Dämpfungsmaß: Unterschied zwischen den Versionen
K (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
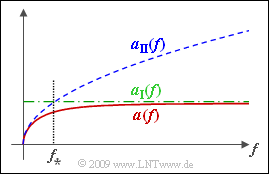
| − | [[Datei:P_ID1797__LZI_A_4_1.png|right|frame|Dämpfungsmaß und Schranken]] | + | [[Datei:P_ID1797__LZI_A_4_1.png|right|frame|Dämpfungsmaß $\alpha(f)$ und zwei Schranken für verschiedene Bereiche]] |
| − | Das Dämpfungsmaß $\alpha(f)$ – sprich „alpha” – einer Leitung gibt die auf die Leitungslänge bezogene Dämpfung an. Diese Größe ist durch die Leitungsbeläge $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0. | + | Das Dämpfungsmaß $\alpha(f)$ – sprich „alpha” – einer Leitung gibt die auf die Leitungslänge bezogene Dämpfung an. Diese Größe ist durch die Leitungsbeläge $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ und $C\hspace{0.08cm}'$ festgelegt, wobei die exakte Gleichung etwas kompliziert ist. Daher wurden zwei leichter handhabbare Näherungen entwickelt: |
| − | :$$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R\hspace{0.05cm}' \cdot \sqrt{{C\hspace{0. | + | :$$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R\hspace{0.05cm}' \cdot \sqrt{{C\hspace{0.08cm}'}/{ L\hspace{0.05cm}'} } + G\hspace{0.08cm}' \cdot \sqrt{{L\hspace{0.05cm}'}/{ C\hspace{0.08cm}'} }\hspace{0.05cm}\right ] |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | :$$\frac{\alpha_{_{\rm II}}(f)}{\rm Np} = \sqrt{1/2 \cdot \omega \cdot {R\hspace{0.05cm}' \cdot C\hspace{0. | + | :$$\frac{\alpha_{_{\rm II}}(f)}{\rm Np} = \sqrt{1/2 \cdot \omega \cdot {R\hspace{0.05cm}' \cdot C\hspace{0.08cm}'} }\hspace{0.1cm} |
\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$ | \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$ | ||
| − | Diese beiden Näherungen sind zusammen mit dem tatsächlichen Verlauf $\alpha(f)$ in der Grafik dargestellt. Der Schnittpunkt von $\alpha_{\rm I}(f)$ und $\alpha_{\rm II}(f)$ ergibt die charakteristische Frequenz $f_∗$ mit folgender Bedeutung: | + | Diese beiden Näherungen sind zusammen mit dem tatsächlichen Verlauf $\alpha(f)$ in der Grafik dargestellt. Der Schnittpunkt von $\alpha_{\rm I}(f)$ und $\alpha_{\rm II}(f)$ ergibt die charakteristische Frequenz $f_∗$ mit folgender Bedeutung: |
| − | *Für $f \gg f_∗$ gilt $α(f) ≈ α_{\rm I}(f)$. | + | *Für $f \gg f_∗$ gilt $α(f) ≈ α_{\rm I}(f)$. |
| − | *Für $f \ll f_∗$ gilt $α(f) ≈ α_{\rm II}(f)$. | + | *Für $f \ll f_∗$ gilt $α(f) ≈ α_{\rm II}(f)$. |
| − | Mit diesen Näherungen soll das Dämpfungsmaß $\alpha(f)$ für ein Nachrichtensignal der Frequenz $f_0 = 2 \ \rm kHz$ ermittelt werden, wobei folgende Übertragungsmedien zu betrachten sind: | + | Mit diesen Näherungen soll das Dämpfungsmaß $\alpha(f)$ für ein Nachrichtensignal der Frequenz $f_0 = 2 \ \rm kHz$ ermittelt werden, wobei folgende Übertragungsmedien zu betrachten sind: |
| − | * ein Kupferkabel mit $0.6 \ \rm mm$ Durchmesser: | + | * ein Kupferkabel mit $0.6 \ \rm mm$ Durchmesser: |
| − | :$$R\hspace{0. | + | :$$R\hspace{0.05cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} |
| − | L\hspace{0. | + | L\hspace{0.03cm}' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} |
| − | G\hspace{0. | + | G\hspace{0.08cm}' = 1\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} |
| − | C\hspace{0. | + | C\hspace{0.08cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm},$$ |
| − | * eine Bronzefreileitung mit $5 \ \rm mm$ Durchmesser: | + | * eine Bronzefreileitung mit $5 \ \rm mm$ Durchmesser: |
| − | :$$R\hspace{0. | + | :$$R\hspace{0.05cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} |
| − | L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | + | L\hspace{0.03cm}' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} |
| − | G\hspace{0. | + | G\hspace{0.08cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} |
| − | C\hspace{0. | + | C\hspace{0.08cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 33: | Zeile 33: | ||
| − | + | Hinweise: | |
| − | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_Ergebnisse_der_Leitungstheorie|Einige Ergebnisse der Leitungstheorie]]. | |
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_Ergebnisse_der_Leitungstheorie|Einige Ergebnisse der Leitungstheorie]]. | ||
| − | *Die Hinweiseinheit „Neper” (Np) in obigen Gleichungen für $α_{\rm I}(f)$ und $α_{\rm II}(f)$ und damit auch für das gesamte Dämpfungsmaß $α(f)$ ergibt sich aus der Tatsache, dass der Betragsfrequenzgang als $|H(f)| = {\rm e}^{-a}$ definiert ist. | + | *Die Hinweiseinheit „Neper” (Np) in obigen Gleichungen für $α_{\rm I}(f)$ und $α_{\rm II}(f)$ und damit auch für das gesamte Dämpfungsmaß $α(f)$ ergibt sich aus der Tatsache, dass der Betragsfrequenzgang als $|H(f)| = {\rm e}^{-a}$ definiert ist. |
| − | *Daraus folgt für die Dämpfung $ a = - {\rm ln} \; |H(f)|$, wobei der Zusammenhang über den natürlichen Logarithmus durch „Neper” (Np) gekennzeichnet wird. | + | *Daraus folgt für die Dämpfung $ a = - {\rm ln} \; |H(f)|$, wobei der Zusammenhang über den natürlichen Logarithmus durch „Neper” (Np) gekennzeichnet wird. |
| − | *Die Einheit des Dämpfungsmaßes $α = a/l$ ist somit „Np/km”. | + | *Die Einheit des Dämpfungsmaßes $α = a/l$ ist somit „Np/km”. |
| Zeile 45: | Zeile 44: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie für das Kupferkabel und das Bronzekabel die angegebene Näherung $\alpha_{\rm I}$ . | + | {Berechnen Sie für das Kupferkabel und das Bronzekabel die angegebene Näherung $\alpha_{\rm I}$ . |
|type="{}"} | |type="{}"} | ||
${\rm Kupfer}\hspace{-0.1cm}:\hspace{0.2cm} \alpha_{\rm I} \ = \ $ { 0.496 3% } $\ \rm Np/km$ | ${\rm Kupfer}\hspace{-0.1cm}:\hspace{0.2cm} \alpha_{\rm I} \ = \ $ { 0.496 3% } $\ \rm Np/km$ | ||
| Zeile 51: | Zeile 50: | ||
| − | {Geben Sie die jeweilige charakteristische Frequenz $f_*$ an, die die Gültigkeitsbereiche der beiden Näherungen begrenzt. | + | {Geben Sie die jeweilige charakteristische Frequenz $f_*$ an, die die Gültigkeitsbereiche der beiden Näherungen begrenzt. |
|type="{}"} | |type="{}"} | ||
${\rm Kupfer}\hspace{-0.1cm}:\hspace{0.2cm} f_* \ = \ $ { 17.2 3% } $\ \rm kHz$ | ${\rm Kupfer}\hspace{-0.1cm}:\hspace{0.2cm} f_* \ = \ $ { 17.2 3% } $\ \rm kHz$ | ||
| Zeile 57: | Zeile 56: | ||
| − | {Geben Sie unter Zuhilfenahme der beiden Näherungen das Dämpfungsmaß für die Frequenz $f_0 = 2 \ \rm kHz$ an. | + | {Geben Sie unter Zuhilfenahme der beiden Näherungen das Dämpfungsmaß für die Frequenz $f_0 = 2 \ \rm kHz$ an. |
|type="{}"} | |type="{}"} | ||
${\rm Kupfer}\hspace{-0.1cm}: \hspace{0.2cm} \alpha (f = f_0) \ = \ $ { 0.17 3% } $\ \rm Np/km$ | ${\rm Kupfer}\hspace{-0.1cm}: \hspace{0.2cm} \alpha (f = f_0) \ = \ $ { 0.17 3% } $\ \rm Np/km$ | ||
| Zeile 68: | Zeile 67: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Für das Kupferkabel gilt mit $R\hspace{0.03cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} | + | '''(1)''' Für das Kupferkabel gilt mit $R\hspace{0.03cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} |
L' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | L' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
G\hspace{0.03cm}' = 1\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | G\hspace{0.03cm}' = 1\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
| Zeile 79: | Zeile 78: | ||
\left [130 \cdot 7.638 \cdot 10^{-3}+ 10^{-6} \cdot 0.131 \cdot 10^{3}\right | \left [130 \cdot 7.638 \cdot 10^{-3}+ 10^{-6} \cdot 0.131 \cdot 10^{3}\right | ||
] {\rm Np/km} \hspace{0.15cm}\underline{= 0.496\,{\rm Np/km}}\hspace{0.05cm}.$$ | ] {\rm Np/km} \hspace{0.15cm}\underline{= 0.496\,{\rm Np/km}}\hspace{0.05cm}.$$ | ||
| − | Für die Bronzeleitung ergibt sich mit $R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} | + | Für die Bronzeleitung ergibt sich mit $R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} |
L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
G\hspace{0.03cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | G\hspace{0.03cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} | C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} | ||
| − | \hspace{0.05cm}: | + | \hspace{0.05cm}$: |
:$$\alpha_{\rm I}(f) = 1/2 \cdot | :$$\alpha_{\rm I}(f) = 1/2 \cdot | ||
\left [2.2 \cdot \sqrt{\frac{6.7 \cdot 10^{-9}}{ 1.8 \cdot 10^{-3}} } | \left [2.2 \cdot \sqrt{\frac{6.7 \cdot 10^{-9}}{ 1.8 \cdot 10^{-3}} } | ||
| Zeile 89: | Zeile 88: | ||
] $$ | ] $$ | ||
:$$ \Rightarrow \; \alpha_{\rm I}(f) = \frac{1 \,\rm Np/km}{2} \cdot | :$$ \Rightarrow \; \alpha_{\rm I}(f) = \frac{1 \,\rm Np/km}{2} \cdot | ||
| − | \ | + | \big [4.244 \cdot 10^{-3}+ 0.259 \cdot 10^{-3}\big |
] {\rm Np/km} | ] {\rm Np/km} | ||
\hspace{0.15cm}\underline{= 0.0023\,{\rm Np}/{ {\rm km} }}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= 0.0023\,{\rm Np}/{ {\rm km} }}\hspace{0.05cm}.$$ | ||
| − | '''(2)''' Die in der Teilaufgabe (1) berechnete Schranke $α_{\rm I}(f)$ gilt nur für $f \gg f_∗$, während die Schranke $α_{\rm II}(f)$ für $f \ll f_∗$ gültig ist. Die charakteristische Frequenz ergibt sich als der Schnittpunkt der beiden Näherungen: | + | '''(2)''' Die in der Teilaufgabe '''(1)''' berechnete Schranke $α_{\rm I}(f)$ gilt nur für $f \gg f_∗$, während die Schranke $α_{\rm II}(f)$ für $f \ll f_∗$ gültig ist. |
| + | *Die charakteristische Frequenz ergibt sich als der Schnittpunkt der beiden Näherungen: | ||
:$$\alpha_{\rm II}(f = f_{\star}) = \sqrt{1/2 \cdot \omega_{\star} \cdot R' \cdot C' }\hspace{0.1cm} | :$$\alpha_{\rm II}(f = f_{\star}) = \sqrt{1/2 \cdot \omega_{\star} \cdot R' \cdot C' }\hspace{0.1cm} | ||
\bigg |_{\omega_{\star} \hspace{0.05cm}= \hspace{0.05cm}2\pi f_{\star}} = \alpha_{\rm I}(f = f_{\star})$$ | \bigg |_{\omega_{\star} \hspace{0.05cm}= \hspace{0.05cm}2\pi f_{\star}} = \alpha_{\rm I}(f = f_{\star})$$ | ||
| − | Für das Kupferkabel mit 0.6 mm Durchmesser gilt folgende Bestimmungsgleichung: | + | *Für das Kupferkabel mit $\text{0.6 mm}$ Durchmesser gilt folgende Bestimmungsgleichung: |
:$$f_{\star} = \frac {{\alpha^2_{_{\rm I}}(f = f_{\star})}}{\pi \cdot R' \cdot C'}= | :$$f_{\star} = \frac {{\alpha^2_{_{\rm I}}(f = f_{\star})}}{\pi \cdot R' \cdot C'}= | ||
\frac {0.496^2 \, {\rm 1/km^2}}{\pi \cdot 130\,{\rm \Omega/km} \cdot 35 \cdot 10^{-9}\,{\rm s/(\Omega \cdot km)}} | \frac {0.496^2 \, {\rm 1/km^2}}{\pi \cdot 130\,{\rm \Omega/km} \cdot 35 \cdot 10^{-9}\,{\rm s/(\Omega \cdot km)}} | ||
\hspace{0.15cm}\underline{= 17.2\,{\rm kHz}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= 17.2\,{\rm kHz}}\hspace{0.05cm}.$$ | ||
| − | Dagegen erhält man für die Bronzeleitung mit 5 mm Durchmesser: | + | *Dagegen erhält man für die Bronzeleitung mit $\text{5 mm}$ Durchmesser: |
:$$f_{\star} = | :$$f_{\star} = | ||
\frac {(2.25 \cdot 10^{-3})^2 }{\pi \cdot 2.2 \cdot 6.7 \cdot 10^{-9}}\,{\rm kHz} | \frac {(2.25 \cdot 10^{-3})^2 }{\pi \cdot 2.2 \cdot 6.7 \cdot 10^{-9}}\,{\rm kHz} | ||
| Zeile 107: | Zeile 107: | ||
| − | '''(3)''' Für das Kupferkabel gilt $f_0 \ll f_∗$. Deshalb ist hier die Näherung $α_{\rm II}(f)$ | + | |
| + | '''(3)''' Für das Kupferkabel gilt $f_0 \ll f_∗$. | ||
| + | *Deshalb ist hier die Näherung $α_{\rm II}(f)$ ⇒ „starke Dämpfung” zu verwenden: | ||
:$$\alpha(f = f_0) \approx \sqrt{\pi \cdot f_0 \cdot R' \cdot C'}= \sqrt{\pi \cdot 2 \cdot 10^{3} \cdot 130 \cdot 35 \cdot 10^{-9}} | :$$\alpha(f = f_0) \approx \sqrt{\pi \cdot f_0 \cdot R' \cdot C'}= \sqrt{\pi \cdot 2 \cdot 10^{3} \cdot 130 \cdot 35 \cdot 10^{-9}} | ||
\hspace{0.1cm}{\rm Np}/{ {\rm km} } | \hspace{0.1cm}{\rm Np}/{ {\rm km} } | ||
\hspace{0.15cm}\underline{ = 0.17 \hspace{0.1cm}{\rm Np}/{ {\rm km} }} | \hspace{0.15cm}\underline{ = 0.17 \hspace{0.1cm}{\rm Np}/{ {\rm km} }} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Für die Bronzeleitung ist wegen $f_0 \gg f_∗$ die Näherung $α_{\rm I}(f)$ ⇒ „schwache Dämpfung” besser geeignet, siehe Teilaufgabe '''(1)''': | |
:$$\alpha(f = f_0) | :$$\alpha(f = f_0) | ||
\hspace{0.15cm}\underline{= 0.0023\hspace{0.1cm}{\rm Np}/{ {\rm km} }} | \hspace{0.15cm}\underline{= 0.0023\hspace{0.1cm}{\rm Np}/{ {\rm km} }} | ||
Aktuelle Version vom 6. November 2021, 16:48 Uhr
Das Dämpfungsmaß $\alpha(f)$ – sprich „alpha” – einer Leitung gibt die auf die Leitungslänge bezogene Dämpfung an. Diese Größe ist durch die Leitungsbeläge $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ und $C\hspace{0.08cm}'$ festgelegt, wobei die exakte Gleichung etwas kompliziert ist. Daher wurden zwei leichter handhabbare Näherungen entwickelt:
- $$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R\hspace{0.05cm}' \cdot \sqrt{{C\hspace{0.08cm}'}/{ L\hspace{0.05cm}'} } + G\hspace{0.08cm}' \cdot \sqrt{{L\hspace{0.05cm}'}/{ C\hspace{0.08cm}'} }\hspace{0.05cm}\right ] \hspace{0.05cm},$$
- $$\frac{\alpha_{_{\rm II}}(f)}{\rm Np} = \sqrt{1/2 \cdot \omega \cdot {R\hspace{0.05cm}' \cdot C\hspace{0.08cm}'} }\hspace{0.1cm} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$
Diese beiden Näherungen sind zusammen mit dem tatsächlichen Verlauf $\alpha(f)$ in der Grafik dargestellt. Der Schnittpunkt von $\alpha_{\rm I}(f)$ und $\alpha_{\rm II}(f)$ ergibt die charakteristische Frequenz $f_∗$ mit folgender Bedeutung:
- Für $f \gg f_∗$ gilt $α(f) ≈ α_{\rm I}(f)$.
- Für $f \ll f_∗$ gilt $α(f) ≈ α_{\rm II}(f)$.
Mit diesen Näherungen soll das Dämpfungsmaß $\alpha(f)$ für ein Nachrichtensignal der Frequenz $f_0 = 2 \ \rm kHz$ ermittelt werden, wobei folgende Übertragungsmedien zu betrachten sind:
- ein Kupferkabel mit $0.6 \ \rm mm$ Durchmesser:
- $$R\hspace{0.05cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L\hspace{0.03cm}' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.08cm}' = 1\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.08cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm},$$
- eine Bronzefreileitung mit $5 \ \rm mm$ Durchmesser:
- $$R\hspace{0.05cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L\hspace{0.03cm}' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.08cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.08cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Ergebnisse der Leitungstheorie.
- Die Hinweiseinheit „Neper” (Np) in obigen Gleichungen für $α_{\rm I}(f)$ und $α_{\rm II}(f)$ und damit auch für das gesamte Dämpfungsmaß $α(f)$ ergibt sich aus der Tatsache, dass der Betragsfrequenzgang als $|H(f)| = {\rm e}^{-a}$ definiert ist.
- Daraus folgt für die Dämpfung $ a = - {\rm ln} \; |H(f)|$, wobei der Zusammenhang über den natürlichen Logarithmus durch „Neper” (Np) gekennzeichnet wird.
- Die Einheit des Dämpfungsmaßes $α = a/l$ ist somit „Np/km”.
Fragebogen
Musterlösung
- $${\alpha_{_{\rm I}}(f)} = \frac{1 \,\rm Np/km}{2} \cdot \left [130\,{\rm \Omega} \cdot \sqrt{\frac{35 \cdot 10^{-9}\,{\rm s/\Omega}}{ 0.6 \cdot 10^{-3}\,{\rm \Omega \,s}} } + 10^{-6}\,{\rm \Omega^{-1}} \cdot \sqrt{\frac{0.6 \cdot 10^{-3}\,{\rm \Omega \,s}}{ 35 \cdot 10^{-9}\,{\rm s/\Omega}} }\hspace{0.1cm}\right ] $$
- $$ \Rightarrow \; \alpha_{\rm I}(f) = 1/2 \cdot \left [130 \cdot 7.638 \cdot 10^{-3}+ 10^{-6} \cdot 0.131 \cdot 10^{3}\right ] {\rm Np/km} \hspace{0.15cm}\underline{= 0.496\,{\rm Np/km}}\hspace{0.05cm}.$$
Für die Bronzeleitung ergibt sich mit $R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}$:
- $$\alpha_{\rm I}(f) = 1/2 \cdot \left [2.2 \cdot \sqrt{\frac{6.7 \cdot 10^{-9}}{ 1.8 \cdot 10^{-3}} } + 0.5 \cdot 10^{-6} \cdot \sqrt{\frac{ 1.8 \cdot 10^{-3}} {6.7 \cdot 10^{-9}}}\hspace{0.1cm}\right ] $$
- $$ \Rightarrow \; \alpha_{\rm I}(f) = \frac{1 \,\rm Np/km}{2} \cdot \big [4.244 \cdot 10^{-3}+ 0.259 \cdot 10^{-3}\big ] {\rm Np/km} \hspace{0.15cm}\underline{= 0.0023\,{\rm Np}/{ {\rm km} }}\hspace{0.05cm}.$$
(2) Die in der Teilaufgabe (1) berechnete Schranke $α_{\rm I}(f)$ gilt nur für $f \gg f_∗$, während die Schranke $α_{\rm II}(f)$ für $f \ll f_∗$ gültig ist.
- Die charakteristische Frequenz ergibt sich als der Schnittpunkt der beiden Näherungen:
- $$\alpha_{\rm II}(f = f_{\star}) = \sqrt{1/2 \cdot \omega_{\star} \cdot R' \cdot C' }\hspace{0.1cm} \bigg |_{\omega_{\star} \hspace{0.05cm}= \hspace{0.05cm}2\pi f_{\star}} = \alpha_{\rm I}(f = f_{\star})$$
- Für das Kupferkabel mit $\text{0.6 mm}$ Durchmesser gilt folgende Bestimmungsgleichung:
- $$f_{\star} = \frac {{\alpha^2_{_{\rm I}}(f = f_{\star})}}{\pi \cdot R' \cdot C'}= \frac {0.496^2 \, {\rm 1/km^2}}{\pi \cdot 130\,{\rm \Omega/km} \cdot 35 \cdot 10^{-9}\,{\rm s/(\Omega \cdot km)}} \hspace{0.15cm}\underline{= 17.2\,{\rm kHz}}\hspace{0.05cm}.$$
- Dagegen erhält man für die Bronzeleitung mit $\text{5 mm}$ Durchmesser:
- $$f_{\star} = \frac {(2.25 \cdot 10^{-3})^2 }{\pi \cdot 2.2 \cdot 6.7 \cdot 10^{-9}}\,{\rm kHz} \hspace{0.15cm}\underline{= 0.109\,{\rm kHz}}\hspace{0.05cm}.$$
(3) Für das Kupferkabel gilt $f_0 \ll f_∗$.
- Deshalb ist hier die Näherung $α_{\rm II}(f)$ ⇒ „starke Dämpfung” zu verwenden:
- $$\alpha(f = f_0) \approx \sqrt{\pi \cdot f_0 \cdot R' \cdot C'}= \sqrt{\pi \cdot 2 \cdot 10^{3} \cdot 130 \cdot 35 \cdot 10^{-9}} \hspace{0.1cm}{\rm Np}/{ {\rm km} } \hspace{0.15cm}\underline{ = 0.17 \hspace{0.1cm}{\rm Np}/{ {\rm km} }} \hspace{0.05cm}.$$
- Für die Bronzeleitung ist wegen $f_0 \gg f_∗$ die Näherung $α_{\rm I}(f)$ ⇒ „schwache Dämpfung” besser geeignet, siehe Teilaufgabe (1):
- $$\alpha(f = f_0) \hspace{0.15cm}\underline{= 0.0023\hspace{0.1cm}{\rm Np}/{ {\rm km} }} \hspace{0.05cm}.$$