Aufgaben:Aufgabe 3.5Z: Anwendung des Residuensatzes: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1781__LZI_Z_3_5.png|right|Sechs | + | [[Datei:P_ID1781__LZI_Z_3_5.png|right|frame|Sechs Pol–Nullstellen–Diagramme]] |
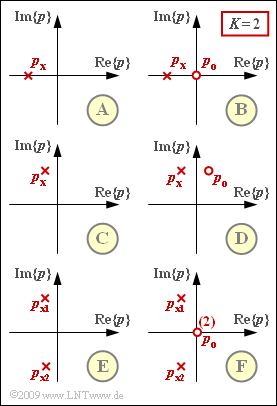
| − | Die Spektralfunktion $Y_{\rm L}(p)$ sei in Pol–Nullstellen–Form gegeben, gekennzeichnet durch | + | Die Spektralfunktion $Y_{\rm L}(p)$ sei in Pol–Nullstellen–Form gegeben, gekennzeichnet durch |
| − | *$Z$ Nullstellen $p_{{\rm o}i}$, | + | *$Z$ Nullstellen $p_{{\rm o}i}$, |
| − | *$N$ | + | *$N$ Pole $p_{{\rm x}i}$, sowie |
| − | *die Konstante $K$. | + | *die Konstante $K$. |
| − | |||
| − | Für den Fall, dass die Anzahl $Z$ der Nullstellen kleiner als die Anzahl $N$ der Pole ist, kann das zugehörige Zeitsignal $y(t)$ durch Anwendung des [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation#Formulierung_des_Residuensatzes|Residuensatzes]] direkt ermittelt werden. In diesem Fall gilt | + | Betrachtet werden im Folgenden die in der Grafik dargestellten Konfigurationen. Es gelte stets $K= 2$. |
| − | $$y(t) = \sum_{i=1}^{I} \left \{ | + | |
| + | Für den Fall, dass die Anzahl $Z$ der Nullstellen kleiner als die Anzahl $N$ der Pole ist, kann das zugehörige Zeitsignal $y(t)$ durch Anwendung des [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation#Formulierung_des_Residuensatzes|Residuensatzes]] direkt ermittelt werden. | ||
| + | |||
| + | In diesem Fall gilt | ||
| + | :$$y(t) = \sum_{i=1}^{I} \left \{ | ||
Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p | Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p | ||
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \right | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \right | ||
| − | \} \hspace{0.05cm} | + | \} \hspace{0.05cm}.$$ |
| − | + | $I$ gibt die Anzahl der unterscheidbaren Pole an; bei allen vorgegebenen Konstellationen ist $I = N$. | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation|Laplace–Rücktransformation]]. | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation|Laplace–Rücktransformation]]. |
| − | + | ||
| − | *Ist das Zeitsignal $y(t)$ komplex, so kann $Y_{\rm L}(p)$ nicht als Schaltung realisiert werden. Die Anwendung des Residuensatzes ist aber | + | *Ist das Zeitsignal $y(t)$ komplex, so kann $Y_{\rm L}(p)$ nicht als Schaltung realisiert werden. Die Anwendung des Residuensatzes ist aber trotzdem möglich. |
| − | *Die komplexe Frequenz $p$, die Nullstellen $p_{{\rm o}i}$ sowie die Pole $p_{{\rm | + | *Die komplexe Frequenz $p$, die Nullstellen $p_{{\rm o}i}$ sowie die Pole $p_{{\rm x}i}$ beschreiben in dieser Aufgabe jeweils normierte Größen ohne Einheit. |
| + | *Damit ist auch die Zeit $t$ dimensionslos. | ||
| Zeile 29: | Zeile 38: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Bei welchen Konfigurationen lässt sich der Residuensatz nicht direkt anwenden? | + | {Bei welchen Konfigurationen lässt sich der Residuensatz <u>nicht direkt</u> anwenden? |
|type="[]"} | |type="[]"} | ||
| − | - Konfiguration A, | + | - Konfiguration $\rm A$, |
| − | + Konfiguration B, | + | + Konfiguration $\rm B$, |
| − | - Konfiguration C, | + | - Konfiguration $\rm C$, |
| − | + Konfiguration D, | + | + Konfiguration $\rm D$, |
| − | - Konfiguration E, | + | - Konfiguration $\rm E$, |
| − | + Konfiguration F | + | + Konfiguration $\rm F$. |
| − | {Berechnen Sie $y(t)$ für die Konfiguration | + | {Berechnen Sie $y(t)$ für die Konfiguration $\rm A$ mit $K= 2$ und $p_{\rm x} = -1$. Welcher Zahlenwert ergibt sich für den Zeitpunkt $t = 1$? |
|type="{}"} | |type="{}"} | ||
| − | + | $\ {\rm Re}\{y(t = 1)\} \ = \ $ { 0.736 3% } | |
| − | $\ {\rm Im}\{y(t = 1)\} \ =$ { 0. } | + | $\ {\rm Im}\{y(t = 1)\} \ = \ $ { 0. } |
| − | {Berechnen Sie $y(t)$ für die Konfiguration | + | {Berechnen Sie $y(t)$ für die Konfiguration $\rm C$ mit $K= 2$ und $p_{\rm x} = -0.2 + {\rm j} \cdot 1.5\pi$. Welcher Zahlenwert ergibt sich für den Zeitpunkt $t = 1$? |
|type="{}"} | |type="{}"} | ||
| − | + | $\ {\rm Re}\{y(t = 1)\} \ = \ $ { 0. } | |
| − | $\ {\rm Im}\{y(t = 1)\} \ =$ { -1.643--1.633 } | + | $\ {\rm Im}\{y(t = 1)\} \ = \ $ { -1.643--1.633 } |
| − | {Welcher Signalwert $y(t = 1)$ ergibt sich bei der Konstellation | + | {Welcher Signalwert $y(t = 1)$ ergibt sich bei der Konstellation $\rm E$ mit $K= 2$ und zwei Polstellen bei $p_{\rm x} = -0.2 \pm {\rm j} \cdot 1.5\pi$? |
|type="{}"} | |type="{}"} | ||
| − | + | $\ {\rm Re}\{y(t = 1)\} \ = \ $ { -0.357--0.337 } | |
| − | $\ {\rm Im}\{y(t = 1)\} \ =$ { 0. } | + | $\ {\rm Im}\{y(t = 1)\} \ = \ $ { 0. } |
| Zeile 62: | Zeile 71: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Voraussetzung für die Anwendung des Residuensatzes ist, dass es weniger Nullstellen als Pole gibt, das heißt, es muss $Z < N$ gelten. Diese Voraussetzung ist | + | '''(1)''' Richtig sind die <u>Lösungsvorschläge 2, 4 und 6</u>: |
| − | $$Y_{\rm L}(p)= \frac {p} {p +1}= 1-\frac {1} {p +1} | + | *Voraussetzung für die Anwendung des Residuensatzes ist, dass es weniger Nullstellen als Pole gibt, das heißt, es muss $Z < N$ gelten. |
| + | *Diese Voraussetzung ist bei den Konfigurationen $\rm B$, $\rm D$ und $\rm F$ nicht gegeben. | ||
| + | *Hier muss zunächst eine Partialbruchzerlegung vorgenommen werden, zum Beispiel für die Konfiguration $\rm B$ mit $p_x = -1$: | ||
| + | :$$Y_{\rm L}(p)= \frac {p} {p +1}= 1-\frac {1} {p +1} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | '''(2)''' Mit $Y_{\rm L}(p) = 2/(p+1)$ ergibt sich aus dem Residuensatz mit $I=1$: | + | |
| − | $$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} | + | '''(2)''' Mit $Y_{\rm L}(p) = 2/(p+1)$ ergibt sich aus dem Residuensatz mit $I=1$: |
| + | :$$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= 2 \cdot {\rm | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= 2 \cdot {\rm | ||
e}^{- \hspace{0.05cm}t}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y(t=1) | e}^{- \hspace{0.05cm}t}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y(t=1) | ||
| Zeile 75: | Zeile 88: | ||
| − | '''(3)''' Bei gleicher Vorgehensweise wie in | + | |
| − | $$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}-(0.2 \hspace{0.05cm}+ | + | [[Datei:P_ID1782__LZI_Z_3_5_c.png|right|frame|Komplexe Signale bei einem einzigen komplexen Pol]] |
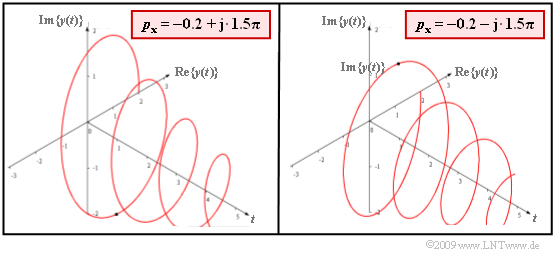
| + | '''(3)''' Bei gleicher Vorgehensweise wie in Teilaufgabe '''(2)''' erhält man nun: | ||
| + | :$$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}-(0.2 \hspace{0.05cm}+ | ||
\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}1.5 \pi) \hspace{0.05cm} \cdot \hspace{0.05cm}t} | \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}1.5 \pi) \hspace{0.05cm} \cdot \hspace{0.05cm}t} | ||
= 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot | = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot | ||
| Zeile 83: | Zeile 98: | ||
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | Aufgrund des zweiten Terms handelt es sich um ein komplexes Signal, dessen Phase in mathematisch positiver Richtung (entgegen dem Uhrzeigersinn) dreht. Für $t=1$ gilt: | + | |
| − | $$y(t = 1) = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2} \cdot \ | + | *Aufgrund des zweiten Terms handelt es sich um ein komplexes Signal, dessen Phase in mathematisch positiver Richtung (entgegen dem Uhrzeigersinn) dreht. Für den Zeitpunkt $t=1$ gilt: |
| + | :$$y(t = 1) = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2} \cdot \big [ | ||
\cos(1.5 \pi) + {\rm j} \cdot \sin(1.5 \pi) | \cos(1.5 \pi) + {\rm j} \cdot \sin(1.5 \pi) | ||
| − | \ | + | \big ]= - {\rm j} \cdot 1.638$$ |
| − | $$\Rightarrow | + | :$$\Rightarrow |
\hspace{0.3cm}{\rm Re}\{y(t = 1)\} \hspace{0.15cm}\underline{ = 0},\hspace{0.2cm} {\rm Im}\{y(t = 1)\} \hspace{0.15cm}\underline{=- 1.638} | \hspace{0.3cm}{\rm Re}\{y(t = 1)\} \hspace{0.15cm}\underline{ = 0},\hspace{0.2cm} {\rm Im}\{y(t = 1)\} \hspace{0.15cm}\underline{=- 1.638} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | Die linke Grafik zeigt das komplexe Signal für einen Pol bei $p_x = -2 + {\rm j} \cdot 1.5 \pi$ . Rechts | + | *Die linke Grafik zeigt das komplexe Signal für einen Pol bei $p_x = -2 + {\rm j} \cdot 1.5 \pi$. Rechts sieht man das dazu konjugiert–komplexe Signal für $p_x = -2 - {\rm j} \cdot 1.5 \pi$. |
| − | |||
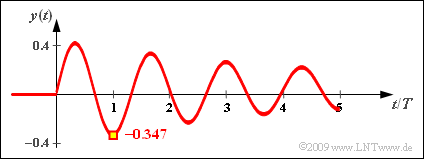
| − | '''(4)''' Nun gilt $I=2$. Die Residien von $p_{x1}$ bzw. $p_{x2}$ liefern: | + | |
| − | $$y_1(t) = | + | [[Datei:P_ID1783__LZI_Z_3_5_d.png|right|frame|Signalverlauf der Konfiguration $\rm E$]] |
| − | \frac {K \cdot (p-p_{{\rm x}1})} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p | + | '''(4)''' Nun gilt $I=2$. Die Residien von $p_{x1}$ bzw. $p_{x2}$ liefern: |
| + | :$$y_1(t) = | ||
| + | \frac {K \cdot (p-p_{{\rm x}1})} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot | ||
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}= | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}= | ||
| − | \frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}1} | + | \frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}1}\hspace{0.05cm}\cdot |
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
\hspace{0.05cm} ,$$ | \hspace{0.05cm} ,$$ | ||
| − | $$ y_2(t) = | + | :$$ y_2(t) = |
| − | \frac {K } { p_{{\rm x}2}-p_{{\rm x}1}} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}2} | + | \frac {K } { p_{{\rm x}2}-p_{{\rm x}1}} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}2}\hspace{0.05cm}\cdot |
\hspace{0.05cm}t}= | \hspace{0.05cm}t}= | ||
| − | -\frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{-p_{{\rm x}1} | + | -\frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{-p_{{\rm x}1}\hspace{0.05cm}\cdot |
\hspace{0.05cm}t}$$ | \hspace{0.05cm}t}$$ | ||
| − | $$ | + | :$$y(t)= y_1(t)+y_2(t) = |
| − | |||
\frac {2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 | \frac {2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 | ||
\hspace{0.08cm}\cdot | \hspace{0.08cm}\cdot | ||
| − | \hspace{0.05cm}t}}{{\rm j} \cdot 3 \pi} \cdot \ | + | \hspace{0.05cm}t}}{{\rm j} \cdot 3 \pi} \cdot \big [ \cos(.) + {\rm j} \cdot \sin(.) |
| − | - \cos(.) + {\rm j} \cdot \sin(.)\ | + | - \cos(.) + {\rm j} \cdot \sin(.)\big ]$$ |
| + | :$$\Rightarrow | ||
| + | \hspace{0.3cm}y(t)= | ||
\frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 | \frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 | ||
\hspace{0.08cm}\cdot | \hspace{0.08cm}\cdot | ||
\hspace{0.05cm}t}\cdot \sin(1.5\pi \cdot t)$$ | \hspace{0.05cm}t}\cdot \sin(1.5\pi \cdot t)$$ | ||
| − | + | :$$\Rightarrow | |
| − | |||
| − | $$\Rightarrow | ||
\hspace{0.3cm}y(t=1)= -\frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 | \hspace{0.3cm}y(t=1)= -\frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 | ||
\hspace{0.08cm}\cdot | \hspace{0.08cm}\cdot | ||
| Zeile 125: | Zeile 141: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | Die Grafik zeigt den (rein reellen) Signalverlauf $y(t)$ für | + | Die Grafik zeigt den (rein reellen) Signalverlauf $y(t)$ für diese Konfiguration. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 10. November 2021, 10:52 Uhr
Die Spektralfunktion $Y_{\rm L}(p)$ sei in Pol–Nullstellen–Form gegeben, gekennzeichnet durch
- $Z$ Nullstellen $p_{{\rm o}i}$,
- $N$ Pole $p_{{\rm x}i}$, sowie
- die Konstante $K$.
Betrachtet werden im Folgenden die in der Grafik dargestellten Konfigurationen. Es gelte stets $K= 2$.
Für den Fall, dass die Anzahl $Z$ der Nullstellen kleiner als die Anzahl $N$ der Pole ist, kann das zugehörige Zeitsignal $y(t)$ durch Anwendung des Residuensatzes direkt ermittelt werden.
In diesem Fall gilt
- $$y(t) = \sum_{i=1}^{I} \left \{ Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \right \} \hspace{0.05cm}.$$
$I$ gibt die Anzahl der unterscheidbaren Pole an; bei allen vorgegebenen Konstellationen ist $I = N$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Laplace–Rücktransformation.
- Ist das Zeitsignal $y(t)$ komplex, so kann $Y_{\rm L}(p)$ nicht als Schaltung realisiert werden. Die Anwendung des Residuensatzes ist aber trotzdem möglich.
- Die komplexe Frequenz $p$, die Nullstellen $p_{{\rm o}i}$ sowie die Pole $p_{{\rm x}i}$ beschreiben in dieser Aufgabe jeweils normierte Größen ohne Einheit.
- Damit ist auch die Zeit $t$ dimensionslos.
Fragebogen
Musterlösung
- Voraussetzung für die Anwendung des Residuensatzes ist, dass es weniger Nullstellen als Pole gibt, das heißt, es muss $Z < N$ gelten.
- Diese Voraussetzung ist bei den Konfigurationen $\rm B$, $\rm D$ und $\rm F$ nicht gegeben.
- Hier muss zunächst eine Partialbruchzerlegung vorgenommen werden, zum Beispiel für die Konfiguration $\rm B$ mit $p_x = -1$:
- $$Y_{\rm L}(p)= \frac {p} {p +1}= 1-\frac {1} {p +1} \hspace{0.05cm} .$$
(2) Mit $Y_{\rm L}(p) = 2/(p+1)$ ergibt sich aus dem Residuensatz mit $I=1$:
- $$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= 2 \cdot {\rm e}^{- \hspace{0.05cm}t}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y(t=1) =\frac{2}{\rm e} \hspace{0.15cm}\underline{ \approx 0.736 \hspace{0.15cm}{\rm (rein\hspace{0.15cm}reell)}} \hspace{0.05cm} .$$
(3) Bei gleicher Vorgehensweise wie in Teilaufgabe (2) erhält man nun:
- $$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}-(0.2 \hspace{0.05cm}+ \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}1.5 \pi) \hspace{0.05cm} \cdot \hspace{0.05cm}t} = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot \hspace{0.05cm}t}\cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.08cm}\cdot \hspace{0.05cm}1.5 \pi\hspace{0.05cm}\cdot \hspace{0.05cm}t} \hspace{0.05cm} .$$
- Aufgrund des zweiten Terms handelt es sich um ein komplexes Signal, dessen Phase in mathematisch positiver Richtung (entgegen dem Uhrzeigersinn) dreht. Für den Zeitpunkt $t=1$ gilt:
- $$y(t = 1) = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2} \cdot \big [ \cos(1.5 \pi) + {\rm j} \cdot \sin(1.5 \pi) \big ]= - {\rm j} \cdot 1.638$$
- $$\Rightarrow \hspace{0.3cm}{\rm Re}\{y(t = 1)\} \hspace{0.15cm}\underline{ = 0},\hspace{0.2cm} {\rm Im}\{y(t = 1)\} \hspace{0.15cm}\underline{=- 1.638} \hspace{0.05cm} .$$
- Die linke Grafik zeigt das komplexe Signal für einen Pol bei $p_x = -2 + {\rm j} \cdot 1.5 \pi$. Rechts sieht man das dazu konjugiert–komplexe Signal für $p_x = -2 - {\rm j} \cdot 1.5 \pi$.
(4) Nun gilt $I=2$. Die Residien von $p_{x1}$ bzw. $p_{x2}$ liefern:
- $$y_1(t) = \frac {K \cdot (p-p_{{\rm x}1})} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}= \frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}1}\hspace{0.05cm}\cdot \hspace{0.05cm}t} \hspace{0.05cm} ,$$
- $$ y_2(t) = \frac {K } { p_{{\rm x}2}-p_{{\rm x}1}} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}2}\hspace{0.05cm}\cdot \hspace{0.05cm}t}= -\frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{-p_{{\rm x}1}\hspace{0.05cm}\cdot \hspace{0.05cm}t}$$
- $$y(t)= y_1(t)+y_2(t) = \frac {2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot \hspace{0.05cm}t}}{{\rm j} \cdot 3 \pi} \cdot \big [ \cos(.) + {\rm j} \cdot \sin(.) - \cos(.) + {\rm j} \cdot \sin(.)\big ]$$
- $$\Rightarrow \hspace{0.3cm}y(t)= \frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot \hspace{0.05cm}t}\cdot \sin(1.5\pi \cdot t)$$
- $$\Rightarrow \hspace{0.3cm}y(t=1)= -\frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot \hspace{0.05cm}t} \hspace{0.15cm}\underline{= -0.347} \hspace{0.05cm} .$$
Die Grafik zeigt den (rein reellen) Signalverlauf $y(t)$ für diese Konfiguration.