Aufgaben:Aufgabe 4.6Z: ISDN-Versorgungsleitungen: Unterschied zwischen den Versionen
Aus LNTwww
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1816__LZI_Z_4_6.png|right|Hauptbündel, Grundbündel und Sternvierer]] | + | [[Datei:P_ID1816__LZI_Z_4_6.png|right|frame|Hauptbündel, Grundbündel und Sternvierer]] |
| − | Bei [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN|ISDN]] ( | + | Bei [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN|$\rm ISDN$]] ("Integrated Services Digital Networks") ist der Endverzweiger (in der Nähe des Teilnehmers) mit einer Ortsvermittlungsstelle (OVSt) durch eine Kupfer–Doppelader verbunden, wobei jeweils zwei Doppeladern zu einem so genannten Sternvierer verdrillt sind. |
| + | *Mehrere solcher Sternvierer sind zu einem Grundbündel, | ||
| + | *mehrere Grundbündel zu einem Hauptbündel zusammengefasst (siehe Grafik). | ||
| − | Im Netz der Deutschen Telekom (ehemals: Deutsche Bundespost) findet man meist Kupferleitungen mit 0.4 mm Aderdurchmesser, für deren Dämpfungs– und Phasenfunktion in [PW95] | + | |
| − | $${{ | + | Im Netz der Deutschen Telekom (ehemals: Deutsche Bundespost) findet man meist Kupferleitungen mit $\text{0.4 mm}$ Aderdurchmesser, für deren Dämpfungs– und Phasenfunktion in [PW95] folgende Gleichungen angegeben werden: |
| + | :$${{a}_{\rm K}(f)}/{\rm dB} = \left [ 5.1 + 14.3 \cdot \left ({f}/{\rm MHz}\right )^{0.59}\right ]\cdot{l}/{\rm km} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | $${b_{\rm K}(f)}/{\rm rad} = \left [ 32.9 \cdot ({f}/{\rm MHz}) + 2.26 \cdot \left ({f}/{\rm MHz}\right )^{0.5}\right ]\cdot {l}/{\rm km} | + | :$${b_{\rm K}(f)}/{\rm rad} = \left [ 32.9 \cdot ({f}/{\rm MHz}) + 2.26 \cdot \left ({f}/{\rm MHz}\right )^{0.5}\right ]\cdot {l}/{\rm km} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Hierbei bezeichnet $l$ die Leitungslänge. | + | Hierbei bezeichnet $l$ die Leitungslänge. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Eigenschaften_von_Kupfer–Doppeladern|Eigenschaften von Kupfer–Doppeladern]]. | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Eigenschaften_von_Kupfer–Doppeladern|Eigenschaften von Kupfer–Doppeladern]]. |
| − | *Weitere Informationen zum Dämpfungsverhalten von Kupferleitungen finden Sie auf der Seite [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN#Vierdraht.E2.80.93_und_Zweidraht.C3.BCbertragung|Vierdraht-und Zweidraht-Übertragung]] im Buch „Beispiele von Nachrichtensystemen”. | + | *Weitere Informationen zum Dämpfungsverhalten von Kupferleitungen finden Sie auf der Seite [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN#Vierdraht.E2.80.93_und_Zweidraht.C3.BCbertragung|Vierdraht- und Zweidraht-Übertragung]] im Buch „Beispiele von Nachrichtensystemen”. |
| − | * | + | |
| − | *[PW95] kennzeichnet folgenden Literaturhinweis: | + | *Sie können zur Überprüfung Ihrer Ergebnisse das interaktive HTML5/JS–Applet [[Applets:Dämpfung_von_Kupferkabeln|Dämpfung von Kupferkabeln]] benutzen. |
| − | + | *[PW95] kennzeichnet folgenden Literaturhinweis: Pollakowski, P.; Wellhausen, H.-W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995. | |
| Zeile 26: | Zeile 36: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wieviele Teilnehmer ( | + | {Wieviele Teilnehmer $(N)$ können über das vorne dargestellte Hauptkabel an eine ISDN–Ortsvermittlungsstelle angeschlossen werden? |
|type="{}"} | |type="{}"} | ||
| − | $N \ =$ { 50 3% } | + | $N \ = \ $ { 50 3% } |
| Zeile 38: | Zeile 48: | ||
| − | {Ein Gleichsignal wird um den Faktor $4$ gedämpft. Wie groß ist die Kabellänge $l$? | + | {Ein Gleichsignal wird um den Faktor $4$ gedämpft. Wie groß ist die Kabellänge $l$? |
|type="{}"} | |type="{}"} | ||
| − | $l \ =$ { 2.36 3% } $\ \rm km$ | + | $l \ = \ $ { 2.36 3% } $\ \rm km$ |
| − | {Welche Dämpfung und Phase ergeben sich so für die Frequenz $f = 120 \ \rm kHz$? | + | {Welche Dämpfung und Phase ergeben sich so für die Frequenz $f = 120 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm | + | $a_{\rm K}(f = 120\ \rm kHz)\ = \ $ { 21.7 3% } $\ \rm dB$ |
| − | $b_{\rm K}(f = 120\ \rm kHz)\ =$ { 11.2 3% } $\ \rm rad$ | + | $b_{\rm K}(f = 120\ \rm kHz)\ = \ $ { 11.2 3% } $\ \rm rad$ |
| Zeile 54: | Zeile 64: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Im Anschlussbereich wird eine Zweidrahtübertragung verwendet. Die möglichen Anschlüsse sind somit gleich der Anzahl der Doppeladern im Hauptkabel: | |
| + | :$$N = 5 \cdot 5 \cdot 2 \hspace{0.15cm}\underline{= 50}.$$ | ||
| − | |||
| − | + | '''(2)''' Richtig sind die <u>Lösungsvorschläge 1 und 2</u>: | |
| + | *Bei Zweidrahtübertragung ist ein Richtungstrennungsverfahren erforderlich, nämlich die so genannte "Gabelschaltung". Diese hat die Aufgabe, dass beim Empfänger $\rm A$ nur das Sendesignal von Teilnehmer $\rm B$ ankommt, nicht jedoch das eigene Sendesignal. Dies gelingt bei schmalbandigen Signalen – zum Beispiel Sprache – im allgemeinen recht gut, jedoch nicht vollständig ⇒ Lösungsvorschlag 1 ist richtig. | ||
| + | *Der Lösungsvorschlag 2 ist ebenfalls zutreffend. Aufgrund von induktiven und kapazitiven Kopplungen kann es zu Übersprechen von der im gleichen Sternvierer befindlichen Doppelader kommen, wobei Nahnebensprechen (das heißt: der störende Sender und der gestörte Empfänger liegen örtlich zusammen) zu größeren Beeinträchtigungen führt als Fernnebensprechen. | ||
| + | *Nicht zutreffend ist dagegen der letzte Lösungsvorschlag. Impulsinterferenzen ⇒ die gegenseitige störende Beeinflussung benachbarter Symbole können zwar durchaus auftreten, hängen aber nicht mit der Zweidrahtübertragung zusammen. Der Grund für solche Impulsinterferenzen sind vielmehr lineare Verzerrungen, bedingt durch einen nichtidealen Dämpfungs– oder Phasenverlauf. | ||
| − | |||
| − | + | ||
| + | '''(3)''' Die Gleichsignal–Dämpfung um den Faktor $4$ kann wie folgt ausgedrückt werden: | ||
:$$a_{\rm K}(f = 0) = 20 \cdot {\rm lg}\,\,(4) = 12.04\,{\rm dB}\hspace{0.05cm}.$$ | :$$a_{\rm K}(f = 0) = 20 \cdot {\rm lg}\,\,(4) = 12.04\,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | + | *Mit dem angegebenen Koeffizienten $\alpha_0 =5.1 \ \rm dB/km$ ergibt sich somit die Leitungslänge $l = 12.04/5.1\; \underline{= 2.36 \ \rm km}$. | |
| + | |||
| + | |||
| − | + | '''(4)''' Mit den angegebenen Gleichungen und $l = 2.36 \ \rm km$ erhält man: | |
| − | :$$a_{\rm K}(f = 120\,{\rm kHz}) = (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB}\hspace{0.15cm}\underline{ \approx 21.7\,{\rm dB}}\hspace{0.05cm}, | + | :$$a_{\rm K}(f = 120\,{\rm kHz}) = (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB}\hspace{0.15cm}\underline{ \approx 21.7\,{\rm dB}}\hspace{0.05cm},$$ |
| − | b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$ | + | :$$b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 23. November 2021, 18:10 Uhr
Hauptbündel, Grundbündel und Sternvierer
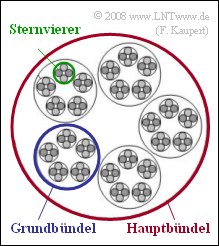
Bei $\rm ISDN$ ("Integrated Services Digital Networks") ist der Endverzweiger (in der Nähe des Teilnehmers) mit einer Ortsvermittlungsstelle (OVSt) durch eine Kupfer–Doppelader verbunden, wobei jeweils zwei Doppeladern zu einem so genannten Sternvierer verdrillt sind.
- Mehrere solcher Sternvierer sind zu einem Grundbündel,
- mehrere Grundbündel zu einem Hauptbündel zusammengefasst (siehe Grafik).
Im Netz der Deutschen Telekom (ehemals: Deutsche Bundespost) findet man meist Kupferleitungen mit $\text{0.4 mm}$ Aderdurchmesser, für deren Dämpfungs– und Phasenfunktion in [PW95] folgende Gleichungen angegeben werden:
- $${{a}_{\rm K}(f)}/{\rm dB} = \left [ 5.1 + 14.3 \cdot \left ({f}/{\rm MHz}\right )^{0.59}\right ]\cdot{l}/{\rm km} \hspace{0.05cm},$$
- $${b_{\rm K}(f)}/{\rm rad} = \left [ 32.9 \cdot ({f}/{\rm MHz}) + 2.26 \cdot \left ({f}/{\rm MHz}\right )^{0.5}\right ]\cdot {l}/{\rm km} \hspace{0.05cm}.$$
Hierbei bezeichnet $l$ die Leitungslänge.
Hinweise:
- Die Aufgabe gehört zum Kapitel Eigenschaften von Kupfer–Doppeladern.
- Weitere Informationen zum Dämpfungsverhalten von Kupferleitungen finden Sie auf der Seite Vierdraht- und Zweidraht-Übertragung im Buch „Beispiele von Nachrichtensystemen”.
- Sie können zur Überprüfung Ihrer Ergebnisse das interaktive HTML5/JS–Applet Dämpfung von Kupferkabeln benutzen.
- [PW95] kennzeichnet folgenden Literaturhinweis: Pollakowski, P.; Wellhausen, H.-W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995.
Fragebogen
Musterlösung
(1) Im Anschlussbereich wird eine Zweidrahtübertragung verwendet. Die möglichen Anschlüsse sind somit gleich der Anzahl der Doppeladern im Hauptkabel:
- $$N = 5 \cdot 5 \cdot 2 \hspace{0.15cm}\underline{= 50}.$$
(2) Richtig sind die Lösungsvorschläge 1 und 2:
- Bei Zweidrahtübertragung ist ein Richtungstrennungsverfahren erforderlich, nämlich die so genannte "Gabelschaltung". Diese hat die Aufgabe, dass beim Empfänger $\rm A$ nur das Sendesignal von Teilnehmer $\rm B$ ankommt, nicht jedoch das eigene Sendesignal. Dies gelingt bei schmalbandigen Signalen – zum Beispiel Sprache – im allgemeinen recht gut, jedoch nicht vollständig ⇒ Lösungsvorschlag 1 ist richtig.
- Der Lösungsvorschlag 2 ist ebenfalls zutreffend. Aufgrund von induktiven und kapazitiven Kopplungen kann es zu Übersprechen von der im gleichen Sternvierer befindlichen Doppelader kommen, wobei Nahnebensprechen (das heißt: der störende Sender und der gestörte Empfänger liegen örtlich zusammen) zu größeren Beeinträchtigungen führt als Fernnebensprechen.
- Nicht zutreffend ist dagegen der letzte Lösungsvorschlag. Impulsinterferenzen ⇒ die gegenseitige störende Beeinflussung benachbarter Symbole können zwar durchaus auftreten, hängen aber nicht mit der Zweidrahtübertragung zusammen. Der Grund für solche Impulsinterferenzen sind vielmehr lineare Verzerrungen, bedingt durch einen nichtidealen Dämpfungs– oder Phasenverlauf.
(3) Die Gleichsignal–Dämpfung um den Faktor $4$ kann wie folgt ausgedrückt werden:
- $$a_{\rm K}(f = 0) = 20 \cdot {\rm lg}\,\,(4) = 12.04\,{\rm dB}\hspace{0.05cm}.$$
- Mit dem angegebenen Koeffizienten $\alpha_0 =5.1 \ \rm dB/km$ ergibt sich somit die Leitungslänge $l = 12.04/5.1\; \underline{= 2.36 \ \rm km}$.
(4) Mit den angegebenen Gleichungen und $l = 2.36 \ \rm km$ erhält man:
- $$a_{\rm K}(f = 120\,{\rm kHz}) = (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB}\hspace{0.15cm}\underline{ \approx 21.7\,{\rm dB}}\hspace{0.05cm},$$
- $$b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$
