Aufgaben:Aufgabe 2.4: Frequenz– und Phasenversatz: Unterschied zwischen den Versionen
K (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID1008__Mod_A_2_4.png|right|frame|Modell des Synchrondemodulators]] | [[Datei:P_ID1008__Mod_A_2_4.png|right|frame|Modell des Synchrondemodulators]] | ||
| − | Betrachtet wird das Quellensignal $q(t) = A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) +A_{\rm 2} \cdot \sin(2 \pi f_{\rm 2} t )$ mit den Signalparametern | + | Betrachtet wird das Quellensignal $q(t) = A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) +A_{\rm 2} \cdot \sin(2 \pi f_{\rm 2} t )$ mit den Signalparametern |
:$$ A_1 = 2\,{\rm V}, \hspace{0.15cm}f_1 = 2\,{\rm kHz} \hspace{0.05cm},$$ | :$$ A_1 = 2\,{\rm V}, \hspace{0.15cm}f_1 = 2\,{\rm kHz} \hspace{0.05cm},$$ | ||
:$$A_2 = 1\,{\rm V}, \hspace{0.15cm}f_2 = 5\,{\rm kHz}\hspace{0.05cm}.$$ | :$$A_2 = 1\,{\rm V}, \hspace{0.15cm}f_2 = 5\,{\rm kHz}\hspace{0.05cm}.$$ | ||
Dieses Signal wird ZSB–amplitudenmoduliert. | Dieses Signal wird ZSB–amplitudenmoduliert. | ||
| − | Das modulierte Signal $s(t)$ besitzt somit Spektralanteile bei $±45$ kHz, $±48$ kHz, $±52$ kHz und $±55$ kHz. Bekannt ist weiter, dass das sendeseitige Trägersignal sinusförmig ist ( | + | Das modulierte Signal $s(t)$ besitzt somit Spektralanteile bei $±45$ kHz, $±48$ kHz, $±52$ kHz und $±55$ kHz. Bekannt ist weiter, dass das sendeseitige Trägersignal sinusförmig ist $(ϕ_{\rm T} = -90^\circ)$. |
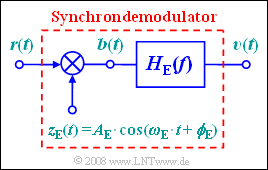
Die Demodulation soll mit der skizzierter Schaltung erfolgen, die durch folgende Parameter bestimmt ist: | Die Demodulation soll mit der skizzierter Schaltung erfolgen, die durch folgende Parameter bestimmt ist: | ||
| − | * Amplitude $A_{\rm E}$ (ohne Einheit), | + | * Amplitude $A_{\rm E}$ (ohne Einheit), |
| − | * Frequenz $f_{\rm E}$, | + | * Frequenz $f_{\rm E}$, |
| − | * Phase $ϕ_{\rm E}$. | + | * Phase $ϕ_{\rm E}$. |
| + | |||
| + | |||
| + | Der Block $H_{\rm E}(f)$ beschreibt einen idealen, rechteckförmigen Tiefpass, der geeignet dimensioniert ist. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Synchrondemodulation|Synchrondemodulation]]. | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Synchrondemodulation|Synchrondemodulation]]. |
| − | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Synchrondemodulation#Einfluss_eines_Frequenzversatzes|Einfluss eines Frequenzversatzes]] und [[Modulationsverfahren/Synchrondemodulation#Einfluss_eines_Phasenversatzes|Einfluss eines Phasenversatzes]]. | + | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Synchrondemodulation#Einfluss_eines_Frequenzversatzes|Einfluss eines Frequenzversatzes]] und [[Modulationsverfahren/Synchrondemodulation#Einfluss_eines_Phasenversatzes|Einfluss eines Phasenversatzes]]. |
*Berücksichtigen Sie die folgenden trigonometrischen Umformungen: | *Berücksichtigen Sie die folgenden trigonometrischen Umformungen: | ||
| Zeile 37: | Zeile 43: | ||
- Der Demodulator würde bei ZSB–AM mit Träger besser arbeiten. | - Der Demodulator würde bei ZSB–AM mit Träger besser arbeiten. | ||
+ Der Träger würde die Sendeleistung unnötigerweise vergrößern. | + Der Träger würde die Sendeleistung unnötigerweise vergrößern. | ||
| − | + Die richtige Dimensionierung des Tiefpasses $H_{\rm E}(f)$ ist essentiell. | + | + Die richtige Dimensionierung des Tiefpasses $H_{\rm E}(f)$ ist essentiell. |
- Man könnte auch einen Hüllkurvendemodulator verwenden. | - Man könnte auch einen Hüllkurvendemodulator verwenden. | ||
| − | + Hüllkurvendemodulation ist nur für $m | + | + Hüllkurvendemodulation ist nur für $m \le 1$ anwendbar. |
| − | {Wie sind die Signalparameter | + | {Wie sind die Signalparameter des empfangsseitigen Trägers $z_{\rm E}(t)$ zu wählen, damit $v(t) = q(t)$ gilt? |
|type="{}"} | |type="{}"} | ||
$A_{\rm E} \ = \ $ { 2 3% } | $A_{\rm E} \ = \ $ { 2 3% } | ||
| Zeile 49: | Zeile 55: | ||
$\phi_{\rm E} \ = \ $ { -94--86 } $\ \text{Grad}$ | $\phi_{\rm E} \ = \ $ { -94--86 } $\ \text{Grad}$ | ||
| − | {Es gelte $f_{\rm E} = f_{\rm T}$ (kein Frequenzversatz). Welches Sinkensignal $v(t)$ ergibt sich mit $ϕ_{\rm E} = - 120^\circ$? Geben Sie dessen Signalwert bei $t = 0$ ein. | + | {Es gelte $f_{\rm E} = f_{\rm T}$ (kein Frequenzversatz). Welches Sinkensignal $v(t)$ ergibt sich mit $ϕ_{\rm E} = - 120^\circ$? <br>Geben Sie dessen Signalwert bei $t = 0$ ein. |
|type="{}"} | |type="{}"} | ||
$v(t = 0)\ = \ $ { 1.732 3% } $\ \text{V}$ | $v(t = 0)\ = \ $ { 1.732 3% } $\ \text{V}$ | ||
| − | {Es gelte weiter $f_{\rm E} = f_{\rm T}$. Welches Sinkensignal $ | + | {Es gelte weiter $f_{\rm E} = f_{\rm T}$. Welches Sinkensignal $v(t)$ ergibt sich mit $ϕ_{\rm E} = 0^\circ$? <br>Geben Sie den Signalwert bei $t = 0$ ein. |
|type="{}"} | |type="{}"} | ||
$v(t = 0)\ = \ $ { 0. } $\ \text{V}$ | $v(t = 0)\ = \ $ { 0. } $\ \text{V}$ | ||
| − | {Es gelte $ϕ_{\rm E} = ϕ_{\rm T}$ (kein Phasenversatz). Welches Sinkensignal erhält man mit $Δ\hspace{-0.05cm}f_{\rm T} = f_{\rm E} | + | {Es gelte $ϕ_{\rm E} = ϕ_{\rm T}$ (kein Phasenversatz). Welches Sinkensignal erhält man mit $Δ\hspace{-0.05cm}f_{\rm T} = f_{\rm E} - f_{\rm T} = 1\text{ kHz}$? |
<br>Welche der folgenden Aussagen sind richtig? | <br>Welche der folgenden Aussagen sind richtig? | ||
|type="[]"} | |type="[]"} | ||
| − | + Es gilt $v(t) = q(t) · \cos(2π · Δ\hspace{-0.05cm}f_{\rm T} · t).$ | + | + Es gilt $v(t) = q(t) · \cos(2π · Δ\hspace{-0.05cm}f_{\rm T} · t).$ |
| − | - $v(t)$ beinhaltet einen Spektralanteil bei $2$ kHz. | + | - $v(t)$ beinhaltet einen Spektralanteil bei $2$ kHz. |
| − | + $v(t)$ beinhaltet einen Spektralanteil bei $4$ kHz. | + | + $v(t)$ beinhaltet einen Spektralanteil bei $4$ kHz. |
| − | + $v(t)$ beinhaltet einen Spektralanteil bei $6$ kHz. | + | + $v(t)$ beinhaltet einen Spektralanteil bei $6$ kHz. |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig sind die <u>Aussagen 2, 3 und 5</u>: | + | '''(1)''' Richtig sind die <u>Aussagen 2, 3 und 5</u>: |
| − | *Bei ZSB–AM ohne Träger bzw. mit einem Modulationsgrad $m > 1$ ist Hüllkurvendemodulation nicht anwendbar. | + | *Bei ZSB–AM ohne Träger bzw. mit einem Modulationsgrad $m > 1$ ist Hüllkurvendemodulation nicht anwendbar. |
| − | *Die Leistungsfähigkeit des Synchrondemodulators wird durch den zusätzlichen Trägeranteil nicht gesteigert, sondern führt lediglich zu einer unnötigen Vergrößerung der aufzubringenden Sendeleistung. | + | *Die Leistungsfähigkeit des Synchrondemodulators wird durch den zusätzlichen Trägeranteil nicht gesteigert, sondern führt lediglich zu einer unnötigen Vergrößerung der aufzubringenden Sendeleistung. |
| − | *Auch die dritte Aussage ist richtig. In der Musterlösung zur Aufgabe 2.4Z wird gezeigt, welche Auswirkungen ein Verzicht bzw. eine falsche Dimensionierung von $H_{\rm E} (f)$ hat. | + | *Auch die dritte Aussage ist richtig. In der Musterlösung zur [[Aufgaben:Aufgabe_2.4Z:_Tiefpass-Einfluss_bei_Synchrondemodulation|Aufgabe 2.4Z]] wird gezeigt, welche Auswirkungen ein Verzicht bzw. eine falsche Dimensionierung von $H_{\rm E} (f)$ hat. |
| − | '''(2)''' Wie der Name „Synchrondemodulator” bereits impliziert, müssen die Signale $z(t)$ und $z_{\rm E} (t)$ frequenz– und phasensynchron sein: | + | |
| + | '''(2)''' Wie der Name „Synchrondemodulator” bereits impliziert, müssen die Signale $z(t)$ und $z_{\rm E} (t)$ frequenz– und phasensynchron sein: | ||
:$$f_{\rm E} = f_{\rm T} \hspace{0.15cm}\underline {= 50\,{\rm kHz}}, \hspace{0.15cm}\phi_{\rm E} = \phi_{\rm T} \hspace{0.15cm}\underline {= - 90^{\circ}} \hspace{0.05cm}.$$ | :$$f_{\rm E} = f_{\rm T} \hspace{0.15cm}\underline {= 50\,{\rm kHz}}, \hspace{0.15cm}\phi_{\rm E} = \phi_{\rm T} \hspace{0.15cm}\underline {= - 90^{\circ}} \hspace{0.05cm}.$$ | ||
| − | Die Trägerfrequenz $f_{\rm T} $ am Sender kann aus den Angaben über das Sendespektrum $S(f)$ ermittelt werden. Bei vollständiger Synchronität gilt: | + | *Die Trägerfrequenz $f_{\rm T} $ am Sender kann aus den Angaben über das Sendespektrum $S(f)$ ermittelt werden. Bei vollständiger Synchronität gilt: |
:$$v(t) = {A_{\rm E}}/{2} \cdot q(t) + {A_{\rm E}}/{2} \cdot q(t)\cdot \cos(2 \cdot \omega_{\rm T} \cdot t ) \hspace{0.05cm}.$$ | :$$v(t) = {A_{\rm E}}/{2} \cdot q(t) + {A_{\rm E}}/{2} \cdot q(t)\cdot \cos(2 \cdot \omega_{\rm T} \cdot t ) \hspace{0.05cm}.$$ | ||
| − | Der zweite Term wird durch den Tiefpass entfernt. Mit $A_{\rm E}\hspace{0.15cm}\underline{ = 2}$ gilt somit $v(t) = q(t)$. | + | *Der zweite Term wird durch den Tiefpass entfernt. Mit $A_{\rm E}\hspace{0.15cm}\underline{ = 2}$ gilt somit $v(t) = q(t)$. |
| − | '''(3)''' Im Theorieteil wurde gezeigt, dass bei ZSB–AM und Synchrondemodulation allgemein gilt: | + | |
| + | '''(3)''' Im Theorieteil wurde gezeigt, dass bei ZSB–AM und Synchrondemodulation allgemein gilt: | ||
:$$v(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t) \hspace{0.05cm}.$$ | :$$v(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t) \hspace{0.05cm}.$$ | ||
| − | Auch bei ungenügender Phasensynchronisation kommt es nicht zu Verzerrungen, sondern nur zu einer frequenzunabhängigen Dämpfung. Mit $ϕ_{\rm T} =-90^\circ$ und $ϕ_{\rm | + | *Auch bei ungenügender Phasensynchronisation kommt es nicht zu Verzerrungen, sondern nur zu einer frequenzunabhängigen Dämpfung. |
| + | *Mit $ϕ_{\rm T} =-90^\circ$ und $ϕ_{\rm E} = -120^\circ$ ist $Δϕ_{\rm T} = -30^\circ$ und man erhält: | ||
:$$ v(t) = \cos(30^{\circ}) \cdot q(t)= 0.866 \cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t= 0) = 0.866 \cdot A_1 \hspace{0.15cm}\underline {= 1.732\,{\rm V}}\hspace{0.05cm}.$$ | :$$ v(t) = \cos(30^{\circ}) \cdot q(t)= 0.866 \cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t= 0) = 0.866 \cdot A_1 \hspace{0.15cm}\underline {= 1.732\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | |||
| − | Das Ergebnis $ | + | '''(4)''' Nun beträgt die Phasendifferenz $Δϕ_{\rm T} = 90^\circ$ und man erhält $v(t) \equiv 0$. |
| + | *Es ist müßig darüber zu diskutieren, ob es sich hierbei noch immer um ein verzerrungsfreies System handelt. | ||
| + | |||
| + | *Das Ergebnis $v(t) \equiv 0$ ist darauf zurückzuführen, dass Cosinus und Sinus orthogonale Funktionen sind. | ||
| + | *Dieses Prinzip wird zum Beispiel bei der so genannten [[Modulationsverfahren/Quadratur–Amplitudenmodulation|Quadratur–Amplitudenmodulation]] ausgenutzt. | ||
| + | |||
'''(5)''' Hier lautet nun die Gleichung für das Signal nach der Multiplikation: | '''(5)''' Hier lautet nun die Gleichung für das Signal nach der Multiplikation: | ||
:$$b(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t - 90^{\circ}) \cdot 2 \cdot \cos(\omega_{\rm E} \cdot t - 90^{\circ})= 2 \cdot q(t) \cdot \sin(\omega_{\rm T} \cdot t ) \cdot \sin(\omega_{\rm E} \cdot t )\hspace{0.05cm}.$$ | :$$b(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t - 90^{\circ}) \cdot 2 \cdot \cos(\omega_{\rm E} \cdot t - 90^{\circ})= 2 \cdot q(t) \cdot \sin(\omega_{\rm T} \cdot t ) \cdot \sin(\omega_{\rm E} \cdot t )\hspace{0.05cm}.$$ | ||
| − | Dieses Ergebnis kann mit der trigonometrischen Umformung | + | *Dieses Ergebnis kann mit der trigonometrischen Umformung |
:$$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right]$$ | :$$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right]$$ | ||
| − | auch wie folgt geschrieben werden: | + | :auch wie folgt geschrieben werden: |
:$$ b(t) = q(t) \cdot \cos((\omega_{\rm T} - \omega_{\rm E}) \cdot t ) + q(t) \cdot \cos((\omega_{\rm T} + \omega_{\rm E}) \cdot t ) \hspace{0.05cm}.$$ | :$$ b(t) = q(t) \cdot \cos((\omega_{\rm T} - \omega_{\rm E}) \cdot t ) + q(t) \cdot \cos((\omega_{\rm T} + \omega_{\rm E}) \cdot t ) \hspace{0.05cm}.$$ | ||
| − | Der zweite Term liegt für $f_{\rm E} | + | *Der zweite Term liegt für $f_{\rm E} = f_{\rm T}$ in der Umgebung von $2f_{\rm T}$ und wird durch den Tiefpass entfernt. |
| + | *Somit bleibt mit der Frequenzdifferenz $Δ\hspace{-0.05cm}f_{\rm T} = f_{\rm E} - f_{\rm T}= 1$ kHz: | ||
:$$ v(t) = q(t) \cdot \cos(2 \pi \cdot \Delta \hspace{-0.05cm}f_{\rm T} \cdot t) \hspace{0.05cm}.$$ | :$$ v(t) = q(t) \cdot \cos(2 \pi \cdot \Delta \hspace{-0.05cm}f_{\rm T} \cdot t) \hspace{0.05cm}.$$ | ||
| − | *Die erste Aussage ist | + | *Die erste Aussage ist richtig. Diese besagt, dass nun das Signal $v(t)$ nach der Demodulation gemäß einer Cosinusfunktion leiser und wieder lauter wird („Schwebung”). |
| − | *Aus dem Cosinusanteil von $q(t)$ mit der Frequenz $f_1 = 2$ | + | *Aus dem Cosinusanteil von $q(t)$ mit der Frequenz $f_1 = 2\text{ kHz}$ werden nun zwei Anteile (jeweils halber Amplitude) bei $1\text{ kHz}$ und $3\text{ kHz}$. |
| − | * Ebenso ist im Sinkensignal kein Anteil bei $f_2 = 5$ | + | * Ebenso ist im Sinkensignal kein Anteil bei $f_2 = 5\text{ kHz}$ enthalten, sondern lediglich Anteile bei $4\text{ kHz}$ und bei $6\text{ kHz}$: |
:$$1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\cdot \cos(2 \pi \cdot 1\,{\rm kHz} \cdot t) = | :$$1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\cdot \cos(2 \pi \cdot 1\,{\rm kHz} \cdot t) = | ||
0.5\,{\rm V} \cdot \sin(2 \pi \cdot 4\,{\rm kHz} \cdot t) | 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 4\,{\rm kHz} \cdot t) | ||
+ 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 6\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ | + 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 6\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ | ||
| − | Richtig sind somit die <u>Aussagen 1, 3 und 4</u>. | + | Richtig sind somit die <u>Aussagen 1, 3 und 4</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 5. Dezember 2021, 14:38 Uhr
Betrachtet wird das Quellensignal $q(t) = A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) +A_{\rm 2} \cdot \sin(2 \pi f_{\rm 2} t )$ mit den Signalparametern
- $$ A_1 = 2\,{\rm V}, \hspace{0.15cm}f_1 = 2\,{\rm kHz} \hspace{0.05cm},$$
- $$A_2 = 1\,{\rm V}, \hspace{0.15cm}f_2 = 5\,{\rm kHz}\hspace{0.05cm}.$$
Dieses Signal wird ZSB–amplitudenmoduliert.
Das modulierte Signal $s(t)$ besitzt somit Spektralanteile bei $±45$ kHz, $±48$ kHz, $±52$ kHz und $±55$ kHz. Bekannt ist weiter, dass das sendeseitige Trägersignal sinusförmig ist $(ϕ_{\rm T} = -90^\circ)$.
Die Demodulation soll mit der skizzierter Schaltung erfolgen, die durch folgende Parameter bestimmt ist:
- Amplitude $A_{\rm E}$ (ohne Einheit),
- Frequenz $f_{\rm E}$,
- Phase $ϕ_{\rm E}$.
Der Block $H_{\rm E}(f)$ beschreibt einen idealen, rechteckförmigen Tiefpass, der geeignet dimensioniert ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Synchrondemodulation.
- Bezug genommen wird insbesondere auf die Seiten Einfluss eines Frequenzversatzes und Einfluss eines Phasenversatzes.
- Berücksichtigen Sie die folgenden trigonometrischen Umformungen:
- $$\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\right] \hspace{0.05cm},$$
- $$\sin(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \sin(\alpha-\beta) + \sin(\alpha+\beta)\right] \hspace{0.05cm},$$
- $$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right] \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- Bei ZSB–AM ohne Träger bzw. mit einem Modulationsgrad $m > 1$ ist Hüllkurvendemodulation nicht anwendbar.
- Die Leistungsfähigkeit des Synchrondemodulators wird durch den zusätzlichen Trägeranteil nicht gesteigert, sondern führt lediglich zu einer unnötigen Vergrößerung der aufzubringenden Sendeleistung.
- Auch die dritte Aussage ist richtig. In der Musterlösung zur Aufgabe 2.4Z wird gezeigt, welche Auswirkungen ein Verzicht bzw. eine falsche Dimensionierung von $H_{\rm E} (f)$ hat.
(2) Wie der Name „Synchrondemodulator” bereits impliziert, müssen die Signale $z(t)$ und $z_{\rm E} (t)$ frequenz– und phasensynchron sein:
- $$f_{\rm E} = f_{\rm T} \hspace{0.15cm}\underline {= 50\,{\rm kHz}}, \hspace{0.15cm}\phi_{\rm E} = \phi_{\rm T} \hspace{0.15cm}\underline {= - 90^{\circ}} \hspace{0.05cm}.$$
- Die Trägerfrequenz $f_{\rm T} $ am Sender kann aus den Angaben über das Sendespektrum $S(f)$ ermittelt werden. Bei vollständiger Synchronität gilt:
- $$v(t) = {A_{\rm E}}/{2} \cdot q(t) + {A_{\rm E}}/{2} \cdot q(t)\cdot \cos(2 \cdot \omega_{\rm T} \cdot t ) \hspace{0.05cm}.$$
- Der zweite Term wird durch den Tiefpass entfernt. Mit $A_{\rm E}\hspace{0.15cm}\underline{ = 2}$ gilt somit $v(t) = q(t)$.
(3) Im Theorieteil wurde gezeigt, dass bei ZSB–AM und Synchrondemodulation allgemein gilt:
- $$v(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t) \hspace{0.05cm}.$$
- Auch bei ungenügender Phasensynchronisation kommt es nicht zu Verzerrungen, sondern nur zu einer frequenzunabhängigen Dämpfung.
- Mit $ϕ_{\rm T} =-90^\circ$ und $ϕ_{\rm E} = -120^\circ$ ist $Δϕ_{\rm T} = -30^\circ$ und man erhält:
- $$ v(t) = \cos(30^{\circ}) \cdot q(t)= 0.866 \cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t= 0) = 0.866 \cdot A_1 \hspace{0.15cm}\underline {= 1.732\,{\rm V}}\hspace{0.05cm}.$$
(4) Nun beträgt die Phasendifferenz $Δϕ_{\rm T} = 90^\circ$ und man erhält $v(t) \equiv 0$.
- Es ist müßig darüber zu diskutieren, ob es sich hierbei noch immer um ein verzerrungsfreies System handelt.
- Das Ergebnis $v(t) \equiv 0$ ist darauf zurückzuführen, dass Cosinus und Sinus orthogonale Funktionen sind.
- Dieses Prinzip wird zum Beispiel bei der so genannten Quadratur–Amplitudenmodulation ausgenutzt.
(5) Hier lautet nun die Gleichung für das Signal nach der Multiplikation:
- $$b(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t - 90^{\circ}) \cdot 2 \cdot \cos(\omega_{\rm E} \cdot t - 90^{\circ})= 2 \cdot q(t) \cdot \sin(\omega_{\rm T} \cdot t ) \cdot \sin(\omega_{\rm E} \cdot t )\hspace{0.05cm}.$$
- Dieses Ergebnis kann mit der trigonometrischen Umformung
- $$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right]$$
- auch wie folgt geschrieben werden:
- $$ b(t) = q(t) \cdot \cos((\omega_{\rm T} - \omega_{\rm E}) \cdot t ) + q(t) \cdot \cos((\omega_{\rm T} + \omega_{\rm E}) \cdot t ) \hspace{0.05cm}.$$
- Der zweite Term liegt für $f_{\rm E} = f_{\rm T}$ in der Umgebung von $2f_{\rm T}$ und wird durch den Tiefpass entfernt.
- Somit bleibt mit der Frequenzdifferenz $Δ\hspace{-0.05cm}f_{\rm T} = f_{\rm E} - f_{\rm T}= 1$ kHz:
- $$ v(t) = q(t) \cdot \cos(2 \pi \cdot \Delta \hspace{-0.05cm}f_{\rm T} \cdot t) \hspace{0.05cm}.$$
- Die erste Aussage ist richtig. Diese besagt, dass nun das Signal $v(t)$ nach der Demodulation gemäß einer Cosinusfunktion leiser und wieder lauter wird („Schwebung”).
- Aus dem Cosinusanteil von $q(t)$ mit der Frequenz $f_1 = 2\text{ kHz}$ werden nun zwei Anteile (jeweils halber Amplitude) bei $1\text{ kHz}$ und $3\text{ kHz}$.
- Ebenso ist im Sinkensignal kein Anteil bei $f_2 = 5\text{ kHz}$ enthalten, sondern lediglich Anteile bei $4\text{ kHz}$ und bei $6\text{ kHz}$:
- $$1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\cdot \cos(2 \pi \cdot 1\,{\rm kHz} \cdot t) = 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 4\,{\rm kHz} \cdot t) + 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 6\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
Richtig sind somit die Aussagen 1, 3 und 4.