Aufgaben:Aufgabe 2.5: ZSB–AM über einen Gaußkanal: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
|||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Modulationsverfahren/Synchrondemodulation}} | {{quiz-Header|Buchseite=Modulationsverfahren/Synchrondemodulation}} | ||
| − | [[Datei:P_ID1010__Mod_A_2_5.png|right|]] | + | [[Datei:P_ID1010__Mod_A_2_5.png|right|frame|ZSB-AM über einen verzerrenden Kanal]] |
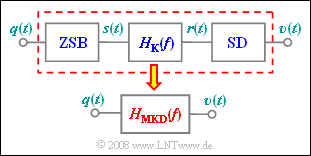
Das hier betrachtete Übertragungssystem setzt sich aus folgenden Blöcken zusammen: | Das hier betrachtete Übertragungssystem setzt sich aus folgenden Blöcken zusammen: | ||
| − | + | *ZSB–AM ohne Träger mit $f_{\rm T} = 50 \ \rm kHz$ bzw. $f_{\rm T} = 55 \ \rm kHz$: | |
| − | $$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$ | + | :$$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$ |
| − | + | * Gaußförmiger Bandpass–Kanal; der Betrag $|f|$ im Exponenten bewirkt, dass $H_K(–f) = H_K(f)$ gilt: | |
| − | $$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left ( | + | :$$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (({|f| - f_{\rm M}})/{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$ |
| − | + | * Synchrondemodulator mit optimalen Kenngrößen, so dass das Sinkensignal $v(t)$ vollständig mit dem Quellensignal $q(t)$ übereinstimmt, wenn $H_{\rm K}(f) = 1$ ist (idealer Kanal). | |
| − | + | ||
| − | Auf der Seite [ | + | |
| − | $$H_{\rm MKD}(f) = | + | Auf der Seite [[Modulationsverfahren/Synchrondemodulation#Einfluss_linearer_Kanalverzerrungen| Einfluss linearer Kanalverzerrungen]] wurde gezeigt, dass das gesamte System durch den resultierenden Frequenzgang |
| − | ausreichend genau charakterisiert ist. Der Index steht hierbei für | + | :$$H_{\rm MKD}(f) = {1}/{2} \cdot \big[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\big]$$ |
| + | ausreichend genau charakterisiert ist. Der Index steht hierbei für $\rm M$odulator – $\rm K$anal – $\rm D$emodulator. | ||
| + | |||
| + | Das Quellensignal $q(t)$ setzt sich aus zwei Cosinus-Schwingungen zusammen: | ||
| + | :$$q(t) = 2\,{\rm V}\cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t)+ 3\,{\rm V}\cdot \cos (2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Synchrondemodulation|Synchrondemodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Synchrondemodulation#Einfluss_linearer_Kanalverzerrungen|Einfluss linearer Kanalverzerrungen]]. | ||
| + | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Zeile 22: | Zeile 36: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie den resultierenden Frequenzgang $H_{MKD}(f)$ für $ | + | {Berechnen Sie den resultierenden Frequenzgang $H_{\rm MKD}(f)$ für $f_{\rm T} = 50 \ \rm kHz$. |
| + | Welche Werte ergeben sich für $f = 1 \ \rm kHz$ und $f = 5 \ \rm kHz$? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $|H_{\rm MKD} (f = 1\ \rm kHz)| \ = \ $ { 0.969 3% } |
| − | $ | + | $|H_{\rm MKD} (f = 5\ \rm kHz)| \ = \ $ { 0.456 3% } |
| − | {Berechnen Sie das Sinkensignal $ | + | {Berechnen Sie das Sinkensignal $v(t)$. Geben Sie die Amplituden $A_1$ und $A_5$ des $1\ \rm kHz$– bzw. $5\ \rm kHz$–Anteils an. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_1 \ = \ $ { 1.938 3% } $\ \text{ V }$ |
| − | $ | + | $A_5 \ = \ $ { 1.368 3% } $\ \text{ V }$ |
| − | {Berechnen Sie den resultierenden Frequenzgang $H_{MKD}(f)$ für $ | + | {Berechnen Sie den resultierenden Frequenzgang $H_{\rm MKD}(f)$ für $f_{\rm T} = 55 \ \rm kHz$. Welche Werte ergeben sich nun für $f = 1 \ \rm kHz$ und $f = 5 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $|H_{\rm MKD} (f = 1\ \rm kHz)| \ = \ $ { 0.463 3% } |
| − | $ | + | $|H_{\rm MKD} (f = 5\ \rm kHz)| \ = \ $ { 0.521 3% } |
| − | {Berechnen Sie das Sinkensignal $ | + | {Berechnen Sie das Sinkensignal $v(t)$. Geben Sie hierfür die Amplituden $A_1$ und $A_5$ der beiden Anteile an. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_1 \ = \ $ { 0.926 3% } $\ \text{ V }$ |
| − | $ | + | $A_5 \ = \ $ { 1.563 3% } $\ \text{ V }$ |
| − | {Gibt es eine Trägerfrequenz $ | + | {Gibt es eine Trägerfrequenz $f_{\rm T}$, die bei dem gegebenen Quellensignal und dem gegebenen Kanal zu keinen Verzerrungen führt? Begründen Sie Ihre Antwort. |
| − | |type=" | + | |type="()"} |
| − | + | + | + Ja, |
| − | - | + | - Nein. |
| Zeile 53: | Zeile 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | [[Datei:P_ID1011__Mod_A_2_5_a.png|right|frame|Resulierender Basisbandfrequenzgang für $f_{\rm T} = f_{\rm M}$]] |
| + | '''(1)''' Die angegebene Gleichung besagt, dass der BP–Frequenzgang $H_{\rm K}(f)$ jeweils um die Trägerfrequenz $f_{\rm T}$ nach links und rechts verschoben und die beiden Anteile aufaddiert werden müssen. | ||
| + | *Es ist noch der Faktor $1/2$ zu berücksichtigen (siehe Skizze). | ||
| + | |||
| + | *Bei niedrigen Frequenzen ergibt sich dann eine Gaußfunktion um die Mittenfrequenz „0”: | ||
| + | :$$H_{\rm MKD}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left ({f}/{\Delta f_{\rm K}}\right)^2} \hspace{0.05cm}.$$ | ||
| + | *Die beiden Anteile bei $±2f_{\rm T}$ müssen nicht weiter betrachtet werden. Für die zwei gesuchten Frequenzen $f_1 = 1\ \rm kHz$ und $f_5 = 5 \ \rm kHz$ erhält man: | ||
| + | :$$ H_{\rm MKD}(f = f_1) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{1\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/100}\hspace{0.15cm}\underline {\approx 0.969} \hspace{0.05cm},$$ | ||
| + | :$$H_{\rm MKD}(f = f_5) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/4} \hspace{0.3cm}\hspace{0.15cm}\underline {\approx 0.456} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(2)''' Mit $ω_1 = 2π · 1\ \rm kHz$ und $ω_5 = 2π · 5 \ \rm kHz$ gilt: | ||
| + | :$$ v(t) = 0.969 \cdot 2\,{\rm V}\cdot \cos (\omega_1 \cdot t)+ 0.456 \cdot 3\,{\rm V}\cdot \cos (\omega_5 \cdot t) = \underline { 1.938\,{\rm V}}\cdot \cos (\omega_1 \cdot t) + \hspace{0.15cm}\underline {1.368\,{\rm V}}\cdot \cos (\omega_5 \cdot t) \hspace{0.05cm}.$$ | ||
| + | *Man erkennt, dass nun – im Gegensatz zum Quellensignal $q(t)$ – der Anteil bei $1 \ \rm kHz$ ⇒ $A_1 = 1.938 \ \rm V$ größer ist als der $5 \ \rm kHz$–Anteil ⇒ $A_5 = 1.368 \ \rm V$, da der Kanal die Frequenzen $49 \ \rm kHz$ und $51 \ \rm kHz$ weniger dämpft als die Spektralanteile bei $45 \ \rm kHz$ und $55 \ \rm kHz$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(3)''' Die beiden um $±f_{\rm T}$ verschobenen Spektralfunktionen kommen nun nicht mehr direkt übereinander zu liegen, sondern sind um $10 \ \rm kHz$ gegeneinander versetzt. | ||
| + | *Der resultierende Frequenzgang $H_{\rm MKD}(f)$ ist somit nicht mehr gaußförmig, sondern es gilt entsprechend der unteren Skizze: | ||
| + | :$$H_{\rm MKD}(f ) = {1}/{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f - 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f + 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right]\hspace{0.05cm}.$$ | ||
| − | + | *Für die Frequenzen $f_1$ und $f_5$ erhält man: | |
| − | |||
| − | + | :$$H_{\rm MKD}(f = 1\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 56\,{\rm kHz}) + H_{\rm K}(f = -54\,{\rm kHz})\right]=$$ | |
| − | [ | + | :$$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{56\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-54\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.161 + 0.302 \hspace{0.15cm}\underline {= 0.463}\hspace{0.05cm},$$ |
| − | $$H_{\rm MKD}(f = | + | :$$H_{\rm MKD}(f = 5\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 60\,{\rm kHz}) + H_{\rm K}(f = -50\,{\rm kHz})\right]= \hspace{0.75cm}$$ |
| − | $$= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{ | + | :$$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{60\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-50\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.022 + 0.500 \hspace{0.15cm}\underline {= 0.521}\hspace{0.05cm}.$$ |
| + | [[Datei:P_ID1012__Mod_A_2_5_c.png|right|frame|Resulierender Basisbandfrequenzgang für $f_{\rm T} \ne f_{\rm M}$]] | ||
| + | *Während bei $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$ der Synchrondemodulator die Information über das Nachrichtensignal aus beiden Seitenbändern in gleicher Weise gewinnt, liefert mit $f_{\rm T} = 55\ \rm kHz$ das untere Seitenband (USB) den größeren Beitrag. | ||
| − | $ | + | |
| − | + | *Zum Beispiel liegt das USB des $5 \ \rm kHz$–Anteils nun genau bei $f_{\rm M} = 50 \ \rm kHz$ und wird ungedämpft übertragen, während das OSB bei $60 \ \rm kHz$ starken Dämpfungen unterliegt. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(4)''' Mit dem Ergebnis der letzten Teilaufgabe erhält man: | ||
| + | :$$ A_1 = 0.463 \cdot 2\,{\rm V}\hspace{0.15cm}\underline { = 0.926\,{\rm V}}\hspace{0.05cm},$$ | ||
| + | :$$A_5 = 0.521 \cdot 3\,{\rm V} \hspace{0.15cm}\underline {= 1.563\,{\rm V}}\hspace{0.05cm}.$$ | ||
| + | *In diesem Fall sind die linearen Verzerrungen sogar weniger stark, da nun auch der $1 \ \rm kHz$–Anteil stärker gedämpft wird. | ||
| − | |||
| − | Dieses Ergebnis gilt allerdings nur für das betrachtete Quellensignal. Ein anderes $q(t)$ mit ebenfalls zwei Spektralanteilen würde eine andere „optimale Trägerfrequenz” erfordern. Bei einem Nachrichtensignal mit drei oder mehr Spektrallinien würde es stets zu linearen Verzerrungen kommen. | + | '''(5)''' Richtig ist JA: |
| + | *Mit der Trägerfrequenz $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$ wird der $5 \ \rm kHz$–Anteil stärker gedämpft als der $1 \ \rm kHz$–Anteil, während mit $f_{\rm T} = 55 \ {\rm kHz} \ne f_{\rm M}$ der $1 \ \rm kHz$–Anteil etwas mehr gedämpft wird. | ||
| + | *Wählt man nun zum Beispiel $f_{\rm T} \approx 54.5 \ \rm kHz$, so werden beide Anteile gleich gedämpft $($etwa um den Faktor $0.53)$ und es gibt keine / weniger Verzerrungen. | ||
| + | *Dieses Ergebnis gilt allerdings nur für das betrachtete Quellensignal. Ein anderes $q(t)$ mit ebenfalls zwei Spektralanteilen würde eine andere „optimale Trägerfrequenz” erfordern. Bei einem Nachrichtensignal mit drei oder mehr Spektrallinien würde es stets zu linearen Verzerrungen kommen. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 6. Dezember 2021, 13:42 Uhr
Das hier betrachtete Übertragungssystem setzt sich aus folgenden Blöcken zusammen:
- ZSB–AM ohne Träger mit $f_{\rm T} = 50 \ \rm kHz$ bzw. $f_{\rm T} = 55 \ \rm kHz$:
- $$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$
- Gaußförmiger Bandpass–Kanal; der Betrag $|f|$ im Exponenten bewirkt, dass $H_K(–f) = H_K(f)$ gilt:
- $$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (({|f| - f_{\rm M}})/{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$
- Synchrondemodulator mit optimalen Kenngrößen, so dass das Sinkensignal $v(t)$ vollständig mit dem Quellensignal $q(t)$ übereinstimmt, wenn $H_{\rm K}(f) = 1$ ist (idealer Kanal).
Auf der Seite Einfluss linearer Kanalverzerrungen wurde gezeigt, dass das gesamte System durch den resultierenden Frequenzgang
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \big[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\big]$$
ausreichend genau charakterisiert ist. Der Index steht hierbei für $\rm M$odulator – $\rm K$anal – $\rm D$emodulator.
Das Quellensignal $q(t)$ setzt sich aus zwei Cosinus-Schwingungen zusammen:
- $$q(t) = 2\,{\rm V}\cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t)+ 3\,{\rm V}\cdot \cos (2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Synchrondemodulation.
- Bezug genommen wird insbesondere auf die Seite Einfluss linearer Kanalverzerrungen.
Fragebogen
Musterlösung
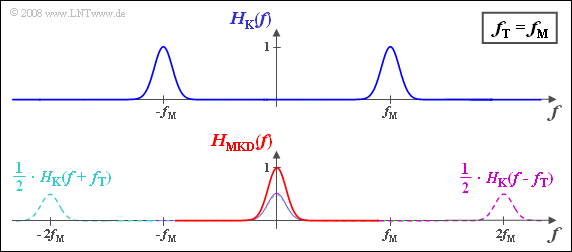
(1) Die angegebene Gleichung besagt, dass der BP–Frequenzgang $H_{\rm K}(f)$ jeweils um die Trägerfrequenz $f_{\rm T}$ nach links und rechts verschoben und die beiden Anteile aufaddiert werden müssen.
- Es ist noch der Faktor $1/2$ zu berücksichtigen (siehe Skizze).
- Bei niedrigen Frequenzen ergibt sich dann eine Gaußfunktion um die Mittenfrequenz „0”:
- $$H_{\rm MKD}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left ({f}/{\Delta f_{\rm K}}\right)^2} \hspace{0.05cm}.$$
- Die beiden Anteile bei $±2f_{\rm T}$ müssen nicht weiter betrachtet werden. Für die zwei gesuchten Frequenzen $f_1 = 1\ \rm kHz$ und $f_5 = 5 \ \rm kHz$ erhält man:
- $$ H_{\rm MKD}(f = f_1) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{1\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/100}\hspace{0.15cm}\underline {\approx 0.969} \hspace{0.05cm},$$
- $$H_{\rm MKD}(f = f_5) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/4} \hspace{0.3cm}\hspace{0.15cm}\underline {\approx 0.456} \hspace{0.05cm}.$$
(2) Mit $ω_1 = 2π · 1\ \rm kHz$ und $ω_5 = 2π · 5 \ \rm kHz$ gilt:
- $$ v(t) = 0.969 \cdot 2\,{\rm V}\cdot \cos (\omega_1 \cdot t)+ 0.456 \cdot 3\,{\rm V}\cdot \cos (\omega_5 \cdot t) = \underline { 1.938\,{\rm V}}\cdot \cos (\omega_1 \cdot t) + \hspace{0.15cm}\underline {1.368\,{\rm V}}\cdot \cos (\omega_5 \cdot t) \hspace{0.05cm}.$$
- Man erkennt, dass nun – im Gegensatz zum Quellensignal $q(t)$ – der Anteil bei $1 \ \rm kHz$ ⇒ $A_1 = 1.938 \ \rm V$ größer ist als der $5 \ \rm kHz$–Anteil ⇒ $A_5 = 1.368 \ \rm V$, da der Kanal die Frequenzen $49 \ \rm kHz$ und $51 \ \rm kHz$ weniger dämpft als die Spektralanteile bei $45 \ \rm kHz$ und $55 \ \rm kHz$.
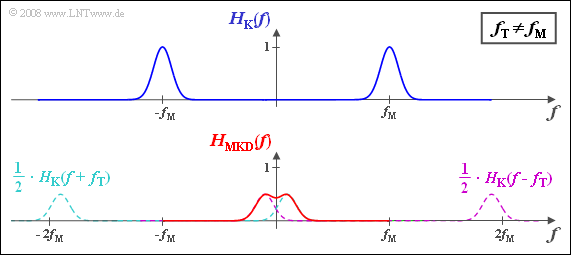
(3) Die beiden um $±f_{\rm T}$ verschobenen Spektralfunktionen kommen nun nicht mehr direkt übereinander zu liegen, sondern sind um $10 \ \rm kHz$ gegeneinander versetzt.
- Der resultierende Frequenzgang $H_{\rm MKD}(f)$ ist somit nicht mehr gaußförmig, sondern es gilt entsprechend der unteren Skizze:
- $$H_{\rm MKD}(f ) = {1}/{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f - 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f + 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right]\hspace{0.05cm}.$$
- Für die Frequenzen $f_1$ und $f_5$ erhält man:
- $$H_{\rm MKD}(f = 1\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 56\,{\rm kHz}) + H_{\rm K}(f = -54\,{\rm kHz})\right]=$$
- $$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{56\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-54\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.161 + 0.302 \hspace{0.15cm}\underline {= 0.463}\hspace{0.05cm},$$
- $$H_{\rm MKD}(f = 5\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 60\,{\rm kHz}) + H_{\rm K}(f = -50\,{\rm kHz})\right]= \hspace{0.75cm}$$
- $$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{60\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-50\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.022 + 0.500 \hspace{0.15cm}\underline {= 0.521}\hspace{0.05cm}.$$
- Während bei $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$ der Synchrondemodulator die Information über das Nachrichtensignal aus beiden Seitenbändern in gleicher Weise gewinnt, liefert mit $f_{\rm T} = 55\ \rm kHz$ das untere Seitenband (USB) den größeren Beitrag.
- Zum Beispiel liegt das USB des $5 \ \rm kHz$–Anteils nun genau bei $f_{\rm M} = 50 \ \rm kHz$ und wird ungedämpft übertragen, während das OSB bei $60 \ \rm kHz$ starken Dämpfungen unterliegt.
(4) Mit dem Ergebnis der letzten Teilaufgabe erhält man:
- $$ A_1 = 0.463 \cdot 2\,{\rm V}\hspace{0.15cm}\underline { = 0.926\,{\rm V}}\hspace{0.05cm},$$
- $$A_5 = 0.521 \cdot 3\,{\rm V} \hspace{0.15cm}\underline {= 1.563\,{\rm V}}\hspace{0.05cm}.$$
- In diesem Fall sind die linearen Verzerrungen sogar weniger stark, da nun auch der $1 \ \rm kHz$–Anteil stärker gedämpft wird.
(5) Richtig ist JA:
- Mit der Trägerfrequenz $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$ wird der $5 \ \rm kHz$–Anteil stärker gedämpft als der $1 \ \rm kHz$–Anteil, während mit $f_{\rm T} = 55 \ {\rm kHz} \ne f_{\rm M}$ der $1 \ \rm kHz$–Anteil etwas mehr gedämpft wird.
- Wählt man nun zum Beispiel $f_{\rm T} \approx 54.5 \ \rm kHz$, so werden beide Anteile gleich gedämpft $($etwa um den Faktor $0.53)$ und es gibt keine / weniger Verzerrungen.
- Dieses Ergebnis gilt allerdings nur für das betrachtete Quellensignal. Ein anderes $q(t)$ mit ebenfalls zwei Spektralanteilen würde eine andere „optimale Trägerfrequenz” erfordern. Bei einem Nachrichtensignal mit drei oder mehr Spektrallinien würde es stets zu linearen Verzerrungen kommen.