Aufgaben:Aufgabe 5.2: Bandspreizung und Schmalbandstörer: Unterschied zwischen den Versionen
Aus LNTwww
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modualtionsverfahren/PN–Modulation }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="[]"…“) |
|||
| (14 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulationsverfahren/PN–Modulation |
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1868__Mod_A_5_2.png|right|frame|Betrachtetes Modell <br>der Bandspreizung]] |
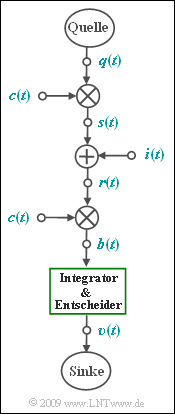
| + | Betrachtet wird ein "Spread Spectrum System" gemäß der vorliegenden Grafik im äquivalenten Tiefpassbereich: | ||
| + | *Das Digitalsignal $q(t)$ besitze das Leistungsdichtespektrum $\rm (LDS)$ ${\it \Phi}_q(f)$, das als rechteckförmig mit der Bandbreite $B = 1/T = 100\ \rm kHz$ angenähert werden soll (eine eher unrealistische Annahme): | ||
| + | :$${\it \Phi}_{q}(f) = | ||
| + | \left\{ \begin{array}{c} {\it \Phi}_{0} \\ | ||
| + | 0 \\ \end{array} \right. | ||
| + | \begin{array}{*{10}c} {\rm{f\ddot{u}r}} | ||
| + | \\ {\rm{sonst}} \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} | ||
| + | |f| <B/2 \hspace{0.05cm}, \\ | ||
| + | \\ | ||
| + | \end{array}$$ | ||
| + | *Im Tiefpassbereich ist somit die Bandbreite (nur die Anteile bei positiven Frequenzen) gleich $B/2$ und die Bandbreite im Bandpassbereich ist $B$. | ||
| + | *Die Bandspreizung erfolgt durch Multiplikation mit der PN–Sequenz $c(t)$ der Chipdauer $T_c = T/100$ <br>(„PN” steht dabei für „Pseudo-Noise”). | ||
| + | *Für die Autokorrelationsfunktion gelte vereinfachend: | ||
| + | :$$ {\it \varphi}_{c}(\tau) = \left\{ \begin{array}{c}1 - |\tau|/T_c \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{sonst}} \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} -T_c \le \tau \le T_c \hspace{0.05cm}, \\ \\ \end{array}$$ | ||
| + | *Beim Empfänger wird wieder die gleiche Spreizfolge $c(t)$ phasensynchron zugesetzt. | ||
| + | *Das Interferenzsignal $i(t)$ soll zunächst vernachlässigt werden. | ||
| + | *In der Teilaufgabe '''(4)''' bezeichnet $i(t)$ einen schmalbandigen Störer bei der Trägerfrequenz $f_{\rm T} = 30 \ \rm MHz = f_{\rm I}$ mit der Leistung $P_{\rm I}$. | ||
| + | *Der Einfluss des (stets vorhandenen) AWGN–Rauschens $n(t)$ wird in dieser Aufgabe nicht betrachtet. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweis:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/PN–Modulation|PN–Modulation]]. | ||
| + | |||
| Zeile 9: | Zeile 38: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie lautet das Leistungsdichtespektrum ${\it \Phi}_c(f )$ des Spreizsignals $c(t)$? Welcher Wert ergibt sich bei der Frequenz $f = 0$? |
| − | |type=" | + | |type="{}"} |
| − | - | + | ${\it \Phi}_c(f = 0) \ = \ $ { 0.1 3% } $\ \cdot 10^{-6} \ \rm 1/Hz$ |
| − | |||
| − | + | {Berechnen Sie die äquivalente Bandbreite $B_c$ des Spreizsignals als Breite des flächengleichen $\rm LDS$–Rechtecks. | |
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $B_c \ = \ $ { 10 3% } $\ \rm MHz$ |
| − | |||
| + | {Welche Aussagen sind für die Bandbreiten der Signale $s(t)$ ⇒ $B_s$ und $b(t)$ ⇒ $B_b$ zutreffend? Die (zweiseitige) Bandbreite von $q(t)$ ist $B$. | ||
| + | |type="[]"} | ||
| + | - $B_s$ ist exakt gleich $B_c$. | ||
| + | + $B_s$ ist näherungsweise gleich $B_c + B$. | ||
| + | - $B_b$ ist exakt gleich $B_s$. | ||
| + | - $B_b$ ist gleich $B_s + B_c = 2B_c + B$. | ||
| + | + $B_b$ ist exakt gleich $B$. | ||
| + | {Welchen Einfluss hat eine Bandspreizung auf einen schmalbandigen Störer bei der Trägerfrequenz? Es gelte also $f_{\rm I} = f_{\rm T}$. | ||
| + | |type="[]"} | ||
| + | + Der störende Einfluss wird durch Bandspreizung abgeschwächt. | ||
| + | - Die Störleistung ist nur mehr halb so groß. | ||
| + | - Die Störleistung wird durch die Bandspreizung nicht verändert. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Das Leistungsdichtesprektrum ${\it \Phi}_c(f)$ ist die Fouriertransformierte der dreieckförmigen AKF, die mit Rechtecken der Breite $T_c$ wie folgt dargestellt werden kann: |
| − | '''2 | + | :$${\it \varphi}_{c}(\tau) = \frac{1}{T_c} \cdot {\rm rect} \big(\frac{\tau}{T_c} \big ) \star {\rm rect} \big(\frac{\tau}{T_c} \big ) \hspace{0.05cm}.$$ |
| − | '''3 | + | *Daraus folgt ${\it \Phi}_{c}(f) = {1}/{T_c} \cdot \big[ T_c \cdot {\rm si} \left(\pi f T_c \right ) \big ] \cdot \big[ T_c \cdot {\rm si} \left(\pi f T_c \right ) \big ] = T_c \cdot {\rm si}^2 \left(\pi f T_c \right ) \hspace{0.05cm}$ mit dem Maximalwert |
| − | '''4 | + | :$${\it \Phi}_{c}(f = 0) = T_c = \frac{T}{100}= \frac{1}{100 \cdot B} = \frac{1}{100 \cdot 10^5\,{\rm 1/s}} = 10^{-7}\,{\rm 1/Hz} \hspace{0.15cm}\underline {= 0.1 \cdot 10^{-6}\,{\rm 1/Hz}}\hspace{0.05cm}.$$ |
| − | + | ||
| − | + | ||
| − | + | ||
| + | '''(2)''' Gemäß Definition gilt mit $T_c = T/100 = 0.1\ \rm µ s$: | ||
| + | [[Datei:P_ID1869__Mod_A_5_2b.png|right|frame|Leistungsdichtespektrum des PN–Spreizsignals]] | ||
| + | |||
| + | :$$B_c= \frac{1}{T_c} \cdot \hspace{-0.03cm} \int_{-\infty }^{+\infty} \hspace{-0.03cm} {\it \Phi}_{c}(f)\hspace{0.1cm} {\rm d}f = \hspace{-0.03cm} \int_{-\infty }^{+\infty} \hspace{-0.03cm} {\rm si}^2 \left(\pi f T_c \right )\hspace{0.1cm} {\rm d}f $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} B_c= \frac{1}{T_c}\hspace{0.15cm}\underline {= 10\,{\rm MHz}} \hspace{0.05cm}$$ | ||
| + | Die Grafik verdeutlicht, | ||
| + | *dass $B_c$ durch die erste Nullstelle der $\rm si^2$–Funktion im äquivalenten Tiefpassbereich vorgegeben wird, | ||
| + | * aber auch gleichzeitig die äquivalente (flächengleiche) Bandbreite im Bandpassbereich angibt. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Richtig sind die <u>Lösungsvorschläge 2 und 5</u>: | ||
| + | *Das LDS ${\it \Phi}_s(f)$ ergibt sich aus der Faltung von ${\it \Phi}_q(f)$ und ${\it \Phi}_c(f)$. Damit erhält man für die Bandbreite des Sendesignals tatsächlich $B_s = B_c + B$. | ||
| + | *Da das Spreizsignal $c(t) ∈ \{+1, –1\}$ mit sich selbst multipliziert immer den Wert $1$ ergibt, ist natürlich $b(t) ≡ q(t)$ und demzufolge $B_b = B$. | ||
| + | *Offensichtlich ist, dass die Bandbreite $B_b$ des bandgestauchten Signals ungleich $2B_c + B$ ist, obwohl die Faltung ${\it \Phi}_s(f) ∗ {\it \Phi}_c(f)$ dies suggeriert. | ||
| + | *Dies hängt damit zusammen, dass nicht die Leistungsdichtespektren gefaltet werden dürfen, sondern von den Spektralfunktionen (Amplitudenspektren) $S(f)$ und $C(f)$ unter Berücksichtigung der Phasenbeziehungen auszugehen ist. | ||
| + | *Erst danach kann aus $B(f)$ das LDS ${\it \Phi}_b(f)$ bestimmt werden. Es gilt offensichtlich auch: $C(f) ∗ C(f) = δ(f)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Richtig ist nur der <u>erste Lösungsvorschlag</u>. Die Lösung soll anhand der Skizze am Seitenende verdeutlicht werden: | ||
| + | *Im oberen Diagramm ist das LDS ${\it \Phi}_i(f)$ des Schmalbandstörers durch zwei Diracfunktionen bei $±f_{\rm T}$ mit Gewichten $P_{\rm I}/2$ angenähert. Eingezeichnet ist auch die Bandbreite $B = 0.1 \ \rm MHz$ (nicht ganz maßstäblich). | ||
| + | |||
| + | *Die empfängerseitige Multiplikation mit $c(t)$ – eigentlich mit der Funktion der Bandstauchung, zumindest bezüglich des Nutzanteils von $r(t)$ – bewirkt hinsichtlich des Störsignals $i(t)$ eine Bandspreizung. Ohne Berücksichtigung des Nutzsignals ist $b(t) = n(t) = i(t) · c(t)$. Daraus folgt: | ||
| + | :$${\it \Phi}_{n}(f) = {\it \Phi}_{i}(f) \star {\it \Phi}_{c}(f) = \frac{P_{\rm I}\cdot T_c}{2}\cdot {\rm si}^2 \left( \pi \cdot (f - f_{\rm T}) \cdot T_c \right )+ \frac{P_{\rm I}\cdot T_c}{2}\cdot {\rm si}^2 \left( \pi \cdot (f + f_{\rm T}) \cdot T_c \right ) \hspace{0.05cm}.$$ | ||
| + | [[Datei:P_ID1870__Mod_A_5_2c.png|right|frame|Leistungsdichtespektren vor und nach der Bandspreizung]] | ||
| + | |||
| + | *Anzumerken ist, dass $n(t)$ hier nur als Abkürzung verwendet wird und nicht AWGN–Rauschen bezeichnet. | ||
| + | *In einem engen Bereich um die Trägerfrequenz $f_{\rm T} = 30 \ \rm MHz$ ist das LDS ${\it \Phi}_n(f)$ nahezu konstant. Damit gilt für die Störleistung nach der Bandspreizung: | ||
| + | :$$ P_{n} = P_{\rm I} \cdot T_c \cdot B = P_{\rm I}\cdot \frac{B}{B_c} = \frac{P_{\rm I}}{J}\hspace{0.05cm}. $$ | ||
| + | *Das bedeutet: Die Störleistung wird durch Bandspreizung um den Faktor $J = T/T_c$ herabgesetzt, weshalb $J$ häufig auch als Spreizgewinn bezeichnet wird. | ||
| + | *Ein solcher Spreizgewinn ist allerdings nur bei einem Schmalbandstörer gegeben. | ||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu | + | [[Category:Aufgaben zu Modulationsverfahren|^5.2 PN–Modulation^]] |
Aktuelle Version vom 8. Dezember 2021, 14:53 Uhr
Betrachtet wird ein "Spread Spectrum System" gemäß der vorliegenden Grafik im äquivalenten Tiefpassbereich:
- Das Digitalsignal $q(t)$ besitze das Leistungsdichtespektrum $\rm (LDS)$ ${\it \Phi}_q(f)$, das als rechteckförmig mit der Bandbreite $B = 1/T = 100\ \rm kHz$ angenähert werden soll (eine eher unrealistische Annahme):
- $${\it \Phi}_{q}(f) = \left\{ \begin{array}{c} {\it \Phi}_{0} \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{sonst}} \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} |f| <B/2 \hspace{0.05cm}, \\ \\ \end{array}$$
- Im Tiefpassbereich ist somit die Bandbreite (nur die Anteile bei positiven Frequenzen) gleich $B/2$ und die Bandbreite im Bandpassbereich ist $B$.
- Die Bandspreizung erfolgt durch Multiplikation mit der PN–Sequenz $c(t)$ der Chipdauer $T_c = T/100$
(„PN” steht dabei für „Pseudo-Noise”). - Für die Autokorrelationsfunktion gelte vereinfachend:
- $$ {\it \varphi}_{c}(\tau) = \left\{ \begin{array}{c}1 - |\tau|/T_c \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{sonst}} \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} -T_c \le \tau \le T_c \hspace{0.05cm}, \\ \\ \end{array}$$
- Beim Empfänger wird wieder die gleiche Spreizfolge $c(t)$ phasensynchron zugesetzt.
- Das Interferenzsignal $i(t)$ soll zunächst vernachlässigt werden.
- In der Teilaufgabe (4) bezeichnet $i(t)$ einen schmalbandigen Störer bei der Trägerfrequenz $f_{\rm T} = 30 \ \rm MHz = f_{\rm I}$ mit der Leistung $P_{\rm I}$.
- Der Einfluss des (stets vorhandenen) AWGN–Rauschens $n(t)$ wird in dieser Aufgabe nicht betrachtet.
Hinweis:
- Die Aufgabe gehört zum Kapitel PN–Modulation.
Fragebogen
Musterlösung
(1) Das Leistungsdichtesprektrum ${\it \Phi}_c(f)$ ist die Fouriertransformierte der dreieckförmigen AKF, die mit Rechtecken der Breite $T_c$ wie folgt dargestellt werden kann:
- $${\it \varphi}_{c}(\tau) = \frac{1}{T_c} \cdot {\rm rect} \big(\frac{\tau}{T_c} \big ) \star {\rm rect} \big(\frac{\tau}{T_c} \big ) \hspace{0.05cm}.$$
- Daraus folgt ${\it \Phi}_{c}(f) = {1}/{T_c} \cdot \big[ T_c \cdot {\rm si} \left(\pi f T_c \right ) \big ] \cdot \big[ T_c \cdot {\rm si} \left(\pi f T_c \right ) \big ] = T_c \cdot {\rm si}^2 \left(\pi f T_c \right ) \hspace{0.05cm}$ mit dem Maximalwert
- $${\it \Phi}_{c}(f = 0) = T_c = \frac{T}{100}= \frac{1}{100 \cdot B} = \frac{1}{100 \cdot 10^5\,{\rm 1/s}} = 10^{-7}\,{\rm 1/Hz} \hspace{0.15cm}\underline {= 0.1 \cdot 10^{-6}\,{\rm 1/Hz}}\hspace{0.05cm}.$$
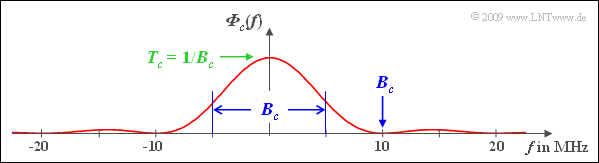
(2) Gemäß Definition gilt mit $T_c = T/100 = 0.1\ \rm µ s$:
- $$B_c= \frac{1}{T_c} \cdot \hspace{-0.03cm} \int_{-\infty }^{+\infty} \hspace{-0.03cm} {\it \Phi}_{c}(f)\hspace{0.1cm} {\rm d}f = \hspace{-0.03cm} \int_{-\infty }^{+\infty} \hspace{-0.03cm} {\rm si}^2 \left(\pi f T_c \right )\hspace{0.1cm} {\rm d}f $$
- $$\Rightarrow \hspace{0.3cm} B_c= \frac{1}{T_c}\hspace{0.15cm}\underline {= 10\,{\rm MHz}} \hspace{0.05cm}$$
Die Grafik verdeutlicht,
- dass $B_c$ durch die erste Nullstelle der $\rm si^2$–Funktion im äquivalenten Tiefpassbereich vorgegeben wird,
- aber auch gleichzeitig die äquivalente (flächengleiche) Bandbreite im Bandpassbereich angibt.
(3) Richtig sind die Lösungsvorschläge 2 und 5:
- Das LDS ${\it \Phi}_s(f)$ ergibt sich aus der Faltung von ${\it \Phi}_q(f)$ und ${\it \Phi}_c(f)$. Damit erhält man für die Bandbreite des Sendesignals tatsächlich $B_s = B_c + B$.
- Da das Spreizsignal $c(t) ∈ \{+1, –1\}$ mit sich selbst multipliziert immer den Wert $1$ ergibt, ist natürlich $b(t) ≡ q(t)$ und demzufolge $B_b = B$.
- Offensichtlich ist, dass die Bandbreite $B_b$ des bandgestauchten Signals ungleich $2B_c + B$ ist, obwohl die Faltung ${\it \Phi}_s(f) ∗ {\it \Phi}_c(f)$ dies suggeriert.
- Dies hängt damit zusammen, dass nicht die Leistungsdichtespektren gefaltet werden dürfen, sondern von den Spektralfunktionen (Amplitudenspektren) $S(f)$ und $C(f)$ unter Berücksichtigung der Phasenbeziehungen auszugehen ist.
- Erst danach kann aus $B(f)$ das LDS ${\it \Phi}_b(f)$ bestimmt werden. Es gilt offensichtlich auch: $C(f) ∗ C(f) = δ(f)$.
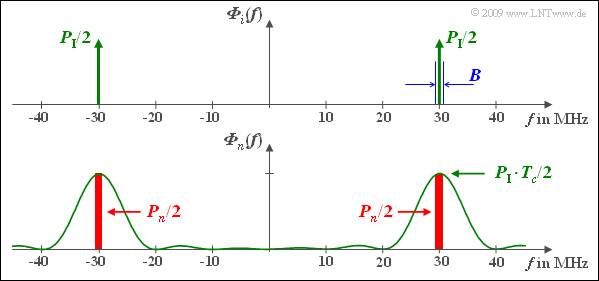
(4) Richtig ist nur der erste Lösungsvorschlag. Die Lösung soll anhand der Skizze am Seitenende verdeutlicht werden:
- Im oberen Diagramm ist das LDS ${\it \Phi}_i(f)$ des Schmalbandstörers durch zwei Diracfunktionen bei $±f_{\rm T}$ mit Gewichten $P_{\rm I}/2$ angenähert. Eingezeichnet ist auch die Bandbreite $B = 0.1 \ \rm MHz$ (nicht ganz maßstäblich).
- Die empfängerseitige Multiplikation mit $c(t)$ – eigentlich mit der Funktion der Bandstauchung, zumindest bezüglich des Nutzanteils von $r(t)$ – bewirkt hinsichtlich des Störsignals $i(t)$ eine Bandspreizung. Ohne Berücksichtigung des Nutzsignals ist $b(t) = n(t) = i(t) · c(t)$. Daraus folgt:
- $${\it \Phi}_{n}(f) = {\it \Phi}_{i}(f) \star {\it \Phi}_{c}(f) = \frac{P_{\rm I}\cdot T_c}{2}\cdot {\rm si}^2 \left( \pi \cdot (f - f_{\rm T}) \cdot T_c \right )+ \frac{P_{\rm I}\cdot T_c}{2}\cdot {\rm si}^2 \left( \pi \cdot (f + f_{\rm T}) \cdot T_c \right ) \hspace{0.05cm}.$$
- Anzumerken ist, dass $n(t)$ hier nur als Abkürzung verwendet wird und nicht AWGN–Rauschen bezeichnet.
- In einem engen Bereich um die Trägerfrequenz $f_{\rm T} = 30 \ \rm MHz$ ist das LDS ${\it \Phi}_n(f)$ nahezu konstant. Damit gilt für die Störleistung nach der Bandspreizung:
- $$ P_{n} = P_{\rm I} \cdot T_c \cdot B = P_{\rm I}\cdot \frac{B}{B_c} = \frac{P_{\rm I}}{J}\hspace{0.05cm}. $$
- Das bedeutet: Die Störleistung wird durch Bandspreizung um den Faktor $J = T/T_c$ herabgesetzt, weshalb $J$ häufig auch als Spreizgewinn bezeichnet wird.
- Ein solcher Spreizgewinn ist allerdings nur bei einem Schmalbandstörer gegeben.