Modulationsverfahren/Spreizfolgen für CDMA: Unterschied zwischen den Versionen
| (25 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Eigenschaften der Korrelationsfunktionen== | ==Eigenschaften der Korrelationsfunktionen== | ||
| − | Wichtige Beurteilungskriterien für Spreizfolgen sind die Korrelationsfunktionen. | + | <br> |
| − | + | Wichtige Beurteilungskriterien für Spreizfolgen sind die Korrelationsfunktionen. | |
| − | |||
| − | $ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ Betrachtet man zwei ergodische Prozesse mit den Musterfunktionen $x(t)$ und $y(t)$, so gilt für die [[Stochastische_Signaltheorie/Kreuzkorrelationsfunktion_und_Kreuzleistungsdichte#Definition_der_Kreuzkorrelationsfunktion|'''Kreuzkorrelationsfunktion''']] $\rm (KKF)$ der Prozesse: | |
| − | + | :$$\varphi_{xy}(\tau)=\overline{x(t)\cdot y(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot y(t+\tau)\,\,\rm d \it t.$$ | |
| − | + | Die überstreichende Linie kennzeichnet hierbei eine Zeitmittelung.}} | |
| − | Setzt man in obiger Gleichung $y(t) = x(t)$, so kommt man zur [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion]] (AKF) | + | $φ_{xy}(τ)$ ist ein quantitatives Maß für die lineare statistische Abhängigkeit der Augenblickswerte von Musterfunktionen $x(t)$ und $y(t + τ)$ der beiden Zufallsprozesse und dient somit der Beschreibung der statistischen Verwandtschaft zwischen diesen. Es gilt: |
| − | :$$ \varphi_{xx}(\tau)=\overline{x(t)\cdot x(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot x(t+\tau)\,\,\rm d \it t$$ | + | *Sind $x(t)$ und $y(t)$ unkorreliert, so ist $φ_{xy}(τ) \equiv 0$ $($also für alle beliebigen Werte von $τ)$. |
| + | *Im allgemeinen ist $φ_{xy}(τ)$ nicht symmetrisch, sondern das KKF–Maximum kann auch durchaus bei $τ_{\rm max} ≠ 0$ auftreten. | ||
| + | *Dann ergibt sich die maximale Korrelation durch eine gegenseitige Verschiebung der beiden betrachteten Signale um die Zeit $τ_{\rm max}$. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
| + | Setzt man in obiger Gleichung $y(t) = x(t)$, so kommt man zur [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|'''Autokorrelationsfunktion''']] $\rm (AKF)$ | ||
| + | :$$ \varphi_{xx}(\tau)=\overline{x(t)\cdot x(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot x(t+\tau)\,\,\rm d \it t$$ | ||
mit folgenden Eigenschaften: | mit folgenden Eigenschaften: | ||
| − | *Die AKF ist ein Maß für die inneren statistischen Bindungen eines durch die Musterfunktion $x(t)$ festgelegten stationären und ergodischen Prozesses. | + | *Die AKF ist ein Maß für die inneren statistischen Bindungen eines durch die Musterfunktion $x(t)$ festgelegten stationären und ergodischen Prozesses. |
| − | *Ist $x(t)$ reell, so ist $φ_{xx}(τ)$ eine reelle gerade Funktion: $φ_{xx}(–τ) = φ_{xx}(τ)$. Phasenbeziehungen gehen in der AKF verloren. | + | *Ist $x(t)$ reell, so ist $φ_{xx}(τ)$ eine reelle gerade Funktion: $φ_{xx}(–τ) = φ_{xx}(τ)$. Phasenbeziehungen gehen also in der AKF verloren. |
| − | *Beschreibt $x(t)$ einen komplexen Prozesse, so ist auch die AKF komplex. | + | *Beschreibt $x(t)$ einen komplexen Prozesse, so ist auch die AKF komplex. |
| − | *Der Maximalwert der AKF liegt bei $τ =0$. Es gilt stets $ | + | *Der Maximalwert der AKF liegt bei $τ =0$. Es gilt stets $\vert φ_{xx}(τ)\vert ≤ φ_{xx}(τ = 0)$, wobei $φ_{xx}(τ =0)$ die Signalleistung $P_x = {\rm E}\big[x^2(t)\big]$ angibt. |
| − | *Der Gleichanteil von $x(t)$ kann aus dem Grenzwert für $ | + | *Der Gleichanteil von $x(t)$ kann aus dem Grenzwert für $τ → ∞$ ermittelt werden, so lange $x(t)$ keine periodischen Anteile beinhaltet: |
| − | :$$\overline{ x(t)} = {\rm E}[x(t)] = \sqrt{\lim_{\tau\to\infty}\,\varphi_{xx} (\tau)} \hspace{0.05cm}.$$ | + | :$$\overline{ x(t)} = {\rm E}\big[x(t)\big] = \sqrt{\lim_{\tau\to\infty}\,\varphi_{xx} (\tau)} \hspace{0.05cm}.$$}} |
| − | + | Autokorrelationsfunktion und Kreuzkorrelationsfunktion beschreiben die inneren Bindungen bzw. die gegenseitigen statistischen Abhängigkeiten im Zeitbereich. Die entsprechenden Beschreibungsfunktionen im Frequenzbereich sind | |
| − | *das [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum]] ${\it Φ}_{xx}(f)$, sowie | + | *das [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum]] ${\it Φ}_{xx}(f)$, sowie |
| − | *das [[Stochastische_Signaltheorie/Kreuzkorrelationsfunktion_und_Kreuzleistungsdichte#Kreuzleistungsdichtespektrum|Kreuzleistungsdichtespektrum]] ${\it Φ}_{xy}(f)$. | + | *das [[Stochastische_Signaltheorie/Kreuzkorrelationsfunktion_und_Kreuzleistungsdichte#Kreuzleistungsdichtespektrum|Kreuzleistungsdichtespektrum]] ${\it Φ}_{xy}(f)$. |
| − | Bei ergodischen Prozessen ergeben sich diese als die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Fouriertransformation|Fouriertransformierten]] von AKF und KKF: | + | Bei ergodischen Prozessen ergeben sich diese als die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Fouriertransformation|Fouriertransformierten]] von AKF und KKF: |
:$${\it \Phi}_{xx}(f) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm}\varphi_{xx}(\tau)\hspace{0.05cm} ,\hspace{0.3cm} {\it \Phi}_{xy}(f) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm}\varphi_{xy}(\tau)\hspace{0.05cm}.$$ | :$${\it \Phi}_{xx}(f) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm}\varphi_{xx}(\tau)\hspace{0.05cm} ,\hspace{0.3cm} {\it \Phi}_{xy}(f) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm}\varphi_{xy}(\tau)\hspace{0.05cm}.$$ | ||
| − | + | ||
| + | Hinweis: Im Folgenden schreiben wir wie im Buch [[Stochastische Signaltheorie]] vereinfachend | ||
| + | *für die AKF $φ_x(τ)$ anstelle von $φ_{xx}(τ)$, | ||
| + | *für das LDS ${\it Φ}_x(f)$ statt ${\it Φ}_{xx}(f)$. | ||
==Periodische AKF und KKF== | ==Periodische AKF und KKF== | ||
| − | Bei periodischen Signalen kann auf den Grenzübergang bei der AKF– und der KKF–Berechnung verzichtet werden, und man erhält mit der Periodendauer $T_0$ (diese muss für beide Signale gleich sein): | + | <br> |
| + | Bei periodischen Signalen kann auf den Grenzübergang bei der AKF– und der KKF–Berechnung verzichtet werden, und man erhält mit der Periodendauer $T_0$ (diese muss für beide Signale gleich sein): | ||
:$$\begin{align*}\varphi_{x}(\tau) & = \frac{1}{T_{\rm 0}}\cdot\int^{T_0}_{0}x(t)\cdot x(t+\tau)\,\,\rm d \it t\hspace{0.05cm} ,\\ | :$$\begin{align*}\varphi_{x}(\tau) & = \frac{1}{T_{\rm 0}}\cdot\int^{T_0}_{0}x(t)\cdot x(t+\tau)\,\,\rm d \it t\hspace{0.05cm} ,\\ | ||
\varphi_{xy}(\tau) & = \frac{1}{T_{\rm 0}}\cdot\int^{T_0}_{0}x(t)\cdot y(t+\tau)\,\,\rm d \it t\hspace{0.05cm}.\end{align*}$$ | \varphi_{xy}(\tau) & = \frac{1}{T_{\rm 0}}\cdot\int^{T_0}_{0}x(t)\cdot y(t+\tau)\,\,\rm d \it t\hspace{0.05cm}.\end{align*}$$ | ||
| − | In diesem Fall ist die AKF ebenfalls eine periodische Funktion, und man spricht von der | + | In diesem Fall ist die AKF ebenfalls eine periodische Funktion, und man spricht von der "periodischen Autokorrelationsfunktion" $\rm (PAKF)$. Diese zeigt folgende Einenschaft: |
:$$\varphi_{x}(\pm T_0) = \varphi_{x}(\pm 2T_0) =\text{ ...} = \varphi_{x}(0) | :$$\varphi_{x}(\pm T_0) = \varphi_{x}(\pm 2T_0) =\text{ ...} = \varphi_{x}(0) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Wir wenden nun obige Berechnungsvorschrift auf das Spreizsignal | Wir wenden nun obige Berechnungsvorschrift auf das Spreizsignal | ||
:$$ c(t) = \sum\limits^{+\infty}_{\nu = -\infty}c_\nu\cdot g_c(t - \nu \cdot T_c)$$ | :$$ c(t) = \sum\limits^{+\infty}_{\nu = -\infty}c_\nu\cdot g_c(t - \nu \cdot T_c)$$ | ||
| − | an, wobei ein Rechteckimpuls $g_c(t)$ der Breite $T_c$ vorausgesetzt wird; $T_c$ nennt man die | + | an, wobei ein Rechteckimpuls $g_c(t)$ der Breite $T_c$ vorausgesetzt wird; $T_c$ nennt man die „Chipdauer”. |
| + | |||
| + | Berücksichtigt man die Periodizität $(T_0 = P · T_c)$ der Koeffizienten $c_ν ∈ \{±1\}$, so ergeben sich die diskreten AKF–Werte bei Vielfachen $($Parameter $λ)$ von $T_c$: | ||
:$$\varphi_{c}(\lambda \cdot T_c) = \frac{1}{P}\cdot\sum\limits^{P-1}_{\nu = 0} c_\nu \cdot c_{\nu+ {\it \lambda} }\hspace{0.05cm}.$$ | :$$\varphi_{c}(\lambda \cdot T_c) = \frac{1}{P}\cdot\sum\limits^{P-1}_{\nu = 0} c_\nu \cdot c_{\nu+ {\it \lambda} }\hspace{0.05cm}.$$ | ||
| − | *Der maximale PAKF–Wert ergibt sich für $λ = 0$ und für Vielfache der Periodenlänge $P$. | + | *Der maximale PAKF–Wert ergibt sich für $λ = 0$ und für Vielfache der Periodenlänge $P$. |
| − | *Aufgrund des rechteckförmigen Impulses $g_c(t)$ ist der PAKF–Verlauf zwischen zwei Abtastwerten $λ · T_c$ und $(λ + 1) · T_c$ stets linear. | + | *Aufgrund des rechteckförmigen Impulses $g_c(t)$ ist der PAKF–Verlauf zwischen zwei Abtastwerten $λ · T_c$ und $(λ + 1) · T_c$ stets linear. |
| − | + | ||
| − | |||
| + | Entsprechend ist die "periodische Kreuzkorrelationsfunktion" $\rm (PKKF)$ zwischen den zwei Spreizfolgen $〈c_ν〉$ und $〈c\hspace{0.04cm}'_ν〉$ gleicher Periodenlänge $P$ wie folgt gegeben: | ||
| + | :$$\varphi_{cc\hspace{0.04cm}'}(\lambda \cdot T_c) = \frac{1}{P}\cdot\sum\limits^{P-1}_{\nu = 0} c_\nu \cdot c\hspace{0.04cm}'_{\nu+ \lambda }\hspace{0.05cm}.$$ | ||
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im | Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im | ||
| − | *Kapitel 9: | + | *Kapitel 9: Stochastische Prozesse, Programm „stp” |
| − | des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf | + | des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf |
| − | *dem Lehrsoftwarepaket [http://www.lntwww.de/downloads/Sonstiges/Programme/LNTsim.zip LNTsim] ⇒ Link verweist auf die ZIP-Version des Programms und | + | *dem Lehrsoftwarepaket [http://www.lntwww.de/downloads/Sonstiges/Programme/LNTsim.zip LNTsim] ⇒ Link verweist auf die ZIP-Version des Programms und |
| − | * | + | *der [http://www.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_B.pdf Praktikumsanleitung] ⇒ Link verweist auf die PDF-Version; Kapitel 9: Seite 207-228. |
==Beurteilungskriterien für PN–Spreizfolgen== | ==Beurteilungskriterien für PN–Spreizfolgen== | ||
| − | Die Qualität eines auf PN–Modulation basierenden CDMA–Systems hängt signifikant von den PAKF– und PKKF–Eigenschaften der verwendeten Spreizfolgen ab. Zusammenfassend kann man sagen: | + | <br> |
| − | *Die PAKF der verwendeten Spreizcodeklasse sollte möglichst durch einen ausgeprägten Peak bei $λ =$ | + | Die Qualität eines auf PN–Modulation basierenden CDMA–Systems hängt signifikant von den PAKF– und PKKF–Eigenschaften der verwendeten Spreizfolgen ab. Zusammenfassend kann man sagen: |
| − | *Der störende Einfluss interferierender CDMA–Teilnehmer lässt sich durch den PKKF–Wert $φ_{cc'} (λ = | + | *Die PAKF der verwendeten Spreizcodeklasse sollte möglichst durch einen ausgeprägten Peak bei ${\it λ} = 0$ gekennzeichnet sein, um die Synchronisation beim Empfänger einfach gestalten zu können. Bei Mehrwegeempfang mit einem Echo der Laufzeitdifferenz $λ · T_c$ ist zudem die Degradation aufgrund von Impulsinterferenzen um so geringer, je kleiner $|φ_c(λ · T_c)|$ ist. |
| − | *Diese letzte Aussage ist in synchronen Systemen mit verzerrungsfreiem Kanal ( | + | *Der störende Einfluss interferierender CDMA–Teilnehmer lässt sich durch den PKKF–Wert $φ_{cc\hspace{0.04cm}'} (λ = 0)$ abschätzen. Ist dieser gleich Null, so spricht man von '''orthogonalen Funktionen'''. Die Fehlerwahrscheinlichkeit wird in diesem Fall nicht erhöht. Sind alle Spreizfolgen orthogonal, so ergibt sich auch bei $J$ Teilnehmern die gleiche Fehlerwahrscheinlichkeit wie bei nur einem einzigen Nutzer. |
| − | + | *Diese letzte Aussage ist in synchronen Systemen mit verzerrungsfreiem Kanal (zum Beispiel bei AWGN) von besonderer Bedeutung. Bei asynchronem Betrieb oder Mehrwegeempfang kommt es dagegen zu einer "De–Orthogonalisierung" und der strengeren Forderung, dass die PKKF zwischen den einzelnen Folgen zu allen Zeitpunkten (betragsmäßig) möglichst kleine Werte annehmen soll. | |
| + | |||
| − | + | Bei der Auswahl von Codefamilien für ein CDMA–System ist weiter darauf zu achten, dass man bei gegebenem Spreizgrad $J = P$ möglichst viele Codefolgen mit günstigen Eigenschaften hinsichtlich dieser drei Kriterien finden kann, um somit auch möglichst viele Teilnehmer gleichzeitig im gleichen Frequenzband versorgen zu können. | |
| − | |||
| + | ==Pseudo–Noise–Folgen maximaler Länge== | ||
| − | [[Datei:P_ID1876__Mod_T_5_3_S4a_neu.png | PN–Generator (Realisierung mit Schieberegister)]] | + | <br> |
| + | Mit einem rückgekoppelten Schieberegister lässt sich eine Folge mit günstigen AKF–Eigenschaften erzeugen, wenn man die Rückführungskoeffizienten $g_i$ mit Index $i = 1, \text{...} \ , G-1$ geeignet wählt. | ||
| + | [[Datei:P_ID1876__Mod_T_5_3_S4a_neu.png|right|frame|PN–Generator (Realisierung mit Schieberegister)]] | ||
| + | |||
| + | [[Datei:P_ID1877__Mod_T_5_3_S4b.png |right|frame| Polynome von M–Sequenzen mit Grad $G$]] | ||
| + | *Die Folge $〈c_ν〉$ ist im strengen Sinne nicht zufällig, sondern periodisch. | ||
| + | *Aufgrund der großen Periodenlänge $P$ erscheint sie aber für einen unbedarften Betrachter als stochastisch. | ||
| + | *Man spricht von einer '''Pseudo–Noise–Folge''' oder kurz "PN–Folge". | ||
| + | |||
| + | |||
| + | $\text{PN–Generatoren}$ haben folgende Eigenschaften, siehe Kapitel [[Stochastische_Signaltheorie/Erzeugung_von_diskreten_Zufallsgrößen|Erzeugung von diskreten Zufallsgrößen]] im Buch „Stochastische Signaltheorie”: | ||
| + | |||
| + | *Die zu früheren Zeitpunkten generierten Binärwerte $c_{ν-1}, \text{...} \ , c_{ν-G}$ sind in den $G$ Speicherzellen des Schieberegisters abgelegt. Man bezeichnet $G$ als den Grad des Schieberegisters. | ||
| + | |||
| + | *Die Koeffizienten $g_1, \ \text{...} \ , g_{G-1}$ sind Binärwerte. Eine „1” kennzeichnet eine Rückführung an der entsprechenden Stelle des Schieberegisters und eine „0” keine Rückführung. | ||
| + | |||
| + | *Für das aktuell erzeugte Symbol gilt mit $g_i ∈ \{0, 1\}$ und $i = 1,\ \text{...}\ , G-1$: | ||
| + | :$$c_\nu = (g_1\cdot c_{\nu-1}+g_2\cdot c_{\nu-2}+\ \text{...}\ +g_i\cdot c_{\nu-i}+\ \text{...}\ +g_{G-1}\cdot c_{\nu-G+1}+ c_{\nu-G})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$ | ||
| + | *Die Modulo–2–Addition kann zum Beispiel durch eine $\rm XOR$–Verknüpfung realisiert werden: | ||
| + | :$$(x + y)\hspace{0.2cm} \rm mod\hspace{0.2cm}2 = {\it x}\hspace{0.2cm}\rm XOR\hspace{0.2cm} {\it y} = \left\{ \begin{array}{*{2}{c}} 0 & \rm falls\hspace{0.1cm} {\it x}= {\it y},\\ 1 & \rm falls\hspace{0.1cm} {\it x}\neq {\it y}. \\ \end{array} \right.$$ | ||
| + | *Sind nicht alle $G$ Speicherzellen mit Nullen vorbelegt, so entsteht eine periodische Zufallsfolge $〈c_ν〉$. Die Periodenlänge $P$ dieser Folge hängt stark von den Rückkopplungskoeffizienten $g_i$ ab. | ||
| + | *Für jeden Grad $G$ gibt es zumindest zwei Konfigurationen mit der hierfür maximalen Periode $P_{\rm max} = 2^G – 1$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In der Tabelle sind für einige Werte von $G$ das Generatorpolynom $G(D)$ einer solchen M–Sequenz und die zugehörige (maximale) Periodenlänge $P$ angegeben, wobei das „M” für „Maximal” steht. Nachfolgend werden die hier gemachten Aussagen am Beispiel $G = 4$ verdeutlicht. | ||
| − | |||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Die Grafik zeigt zwei mögliche Anordnungen zur Erzeugung einer PN–Folge maximaler Länge für $G = 4$ ⇒ $P = 15$. | ||
| + | [[Datei:P_ID1878__Mod_T_5_3_S4c_ganz_neu.png|right|frame| PN–Generatoren vom Grad $G = 4$]] | ||
| + | |||
| + | *Als Kurzbezeichnung wird meist die Oktaldarstellung der Binärzahl $(g_G, \ \text{...} \ ,g_2, g_1, g_0)$ gewählt. Grundsätzlich ist $g_0 = g_G = 1$ zu setzen. | ||
| − | + | *Die linke Konfiguration wird mit $\rm (11001)_{binär} = (31)_{oktal}$ bezeichnet, das dazugehörige Generatorpolynom lautet: | |
| + | :$$G_1(D) = D^4 + D^3 +1\hspace{0.05cm}.$$ | ||
| + | *Die rechte Anordnung mit $\rm (10011)_{binär} = (23)_{oktal}$ ist dagegen durch folgendes Polynom beschreibbar: | ||
| + | :$$G_{\rm 2}(D) =D^4 + D +1 \hspace{0.05cm}.$$ | ||
| + | *Das Polynom $G_2(D)$ ist reziprok zu $G_{\rm 1}(D)$: | ||
| + | :$$G_{\rm 2}(D) = D^4 \cdot (D^{-4} + D^{-3} +1) =D^4 + D +1 \hspace{0.05cm}.$$ | ||
| − | + | Da sowohl $G_1(D)$ als auch $G_{\rm 2}(D)$ [[Kanalcodierung/Erweiterungskörper#Bin.C3.A4re_Erweiterungsk.C3.B6rper_.E2.80.93_Primitive_Polynome|primitive Generatorpolynome]] darstellen (der Nachweis hierfür ist nicht einfach), haben beide Ausgangsfolgen die für $G = 4$ maximale Periodenlänge $P = 15$. Wie in der [[Aufgaben:5.3_PAKF_von_PN–Sequenzen|Aufgabe 5.3]] gezeigt wird, ergibt sich die PAKF in der unipolaren Darstellung ⇒ $c_ν ∈ \{0, 1\}$ zu | |
| − | + | [[Datei: P_ID1879__Mod_T_5_3_S4d_ganz_neu.png|right|frame|PAKF einer PN–Sequenz maximaler Länge $P = 2^G – 1$]] | |
| − | |||
| − | |||
| − | $ | ||
| + | :$${\it \varphi}_{c{\rm ,\hspace{0.05cm}unipolar} }(\lambda \cdot T_c) = \left\{ \begin{array}{c}(P+1)/(2P) \\ (P+1)/(4P) \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r} } \\ {\rm{sonst} } \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} \lambda = 0, \pm P, \pm 2P, \text{...} \hspace{0.05cm} \\ \\ \end{array}$$ | ||
| + | Nach Umsetzung in bipolare Koeffizienten $($das heißt: $0 \ ⇒ +1$, $1 \ ⇒ -1)$ erhält man: | ||
| + | :$${\it \varphi}_{c{\rm ,\hspace{0.05cm}bipolar} }(\lambda \cdot T_c) = \left\{ \begin{array}{c}1 \\ | ||
| + | -P \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r} } \\ {\rm{sonst.} } \hspace{0.05cm} \\ \end{array}\begin{array}{*{20}c} \lambda = 0, \pm P, \pm 2P, \text{...} \hspace{0.05cm} \\ \\ \end{array}$$ | ||
| + | *Man erkennt aus der unteren Skizze die gewünschten ausgeprägten PAKF–Peaks in Abständen der Periode $P$. | ||
| + | *Weniger gut sind die PAKF–Eigenschaften der PN–Sequenzen, wie im Kapitel [[Modulationsverfahren/Fehlerwahrscheinlichkeit_der_PN–Modulation|Fehlerwahrscheinlichkeit der PN–Modulation]] gezeigt werden wird.}} | ||
| − | + | Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im | |
| + | *Kapitel 2: Pseudonoise–Generatoren, Programm „png” | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf | ||
| + | *dem Lehrsoftwarepaket [http://www.lntwww.de/downloads/Sonstiges/Programme/LNTsim.zip LNTsim] ⇒ Link verweist auf die ZIP-Version des Programms und | ||
| + | *der [http://www.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_A.pdf Praktikumsanleitung] ⇒ Link verweist auf die PDF-Version; Kapitel 2: Seite 23-32. | ||
| − | |||
==Codefamilien mit M–Sequenzen== | ==Codefamilien mit M–Sequenzen== | ||
| − | Bei CDMA wird für jeden Teilnehmer eine spezifische Spreizfolge gleicher Periodenlänge | + | <br> |
| + | Bei CDMA wird für jeden Teilnehmer eine spezifische Spreizfolge gleicher Periodenlänge benötigt. Als '''Codefamilie''' bezeichnet man eine (möglichst große) Menge an Spreizsequenzen gleicher Periodenlänge $P$, gültig jeweils für einen Registergrad $G$. | ||
| − | Die Tabelle zeigt, dass die Anzahl von PN–Sequenzen maximaler Länge sehr gering ist. | + | Die Tabelle zeigt, dass die Anzahl von PN–Sequenzen maximaler Länge sehr gering ist. Für den Grad $G = 5$ ⇒ $P = 31$ gibt es zum Beispiel gerade einmal sechs M–Sequenzen, nämlich die PN–Generatoren mit den Oktalkennungen $(45),\ (51),\ (57),\ (67),\ (73)$ und $(75)$. |
| + | Des Weiteren ist in der Literatur auch der Begriff '''Mächtigkeit''' der Codefamilie zu finden. | ||
| + | [[Datei:P_ID1880__Mod_T_5_3_S5_neu.png |right|frame| Mächtigkeit von M–Sequenz–Codefamilien]] | ||
| − | [ | + | *Diese Größe gibt an, wie viele M–Sequenzen und damit gleichzeitige CDMA–Teilnehmer möglich sind, wenn man fordert, dass alle Codepaare „günstige PKKF–Eigenschaften” aufweisen. |
| + | *Aus Platzgründen kann hier nicht explizit ausgeführt werden, was man unter „günstig” genau zu verstehen hat. Hierzu sei auf die Originalliteratur verwiesen, zum Beispiel [ZP85]<ref>Ziemer, R.; Peterson, R. L.: Digital Communication and Spread Spectrum Systems. New York: McMillon, 1985.</ref>. | ||
| − | + | Die letzte Zeile in obiger Tabelle macht deutlich, dass die Mächtigkeit von M–Sequenz–Codefamilien äußerst beschränkt ist, auch bei großem $G$ und damit großer Periodenlänge $P$. | |
| − | + | Ist $G$ ein Vielfaches von $4$ ⇒ $P = 15$, $P = 255$, $P = 4095$ usw., so gibt es grundsätzlich keine günstigen Paare. | |
==Gold–Codes== | ==Gold–Codes== | ||
| − | Um größere Codefamilien zu erhalten | + | <br> |
| + | Um größere Codefamilien zu erhalten als mit M–Sequenzen, müssen die Anforderungen an die periodische Kreuzkorrelationsfunktion $\rm (PKKF)$ abgeschwächt werden. Mit dieser Einschränkung erhält man Codefamilien mit einer weitaus größeren Mächtigkeit, so dass auch mehr CDMA–Teilnehmer versorgt werden können. | ||
| + | [[Datei:P_ID1881__Mod_T_5_3_S6_neu.png|right|frame|Gold–Codegenerator $(51, 75)$ vom Grad $G = 5$]] | ||
| − | + | Gold–Codes verwenden dieses Prinzip. Die Vorschrift zur Erzeugung einer '''Gold–Code–Familie''' $\rm (GCF)$ lautet, wobei ein „+” eine Modulo–2–Addition bezeichnet: | |
| − | + | :$${\rm GCF}(C_1, C_2) = \{ C_1, C_2, C_1 + C_2, C_1 + D \cdot C_2, C_1 + D^2 \cdot C_2, \ \text{...} \ , | |
| − | |||
| − | Gold–Codes verwenden dieses Prinzip. Die Vorschrift zur Erzeugung einer Gold–Code–Familie (GCF) lautet, wobei ein „+” eine Modulo–2–Addition bezeichnet: | ||
| − | $$GCF(C_1, C_2) = \{ C_1, C_2, C_1 + C_2, C_1 + D \cdot C_2, C_1 + D^2 \cdot C_2, ... , | ||
C_1 + D^{P-1} \cdot C_2 \} \hspace{0.05cm}.$$ | C_1 + D^{P-1} \cdot C_2 \} \hspace{0.05cm}.$$ | ||
| − | Das Prinzip ist in der | + | Das Prinzip ist in der Grafik an einem Beispiel dargestellt: |
| − | *Die Folgen $C_1$ und $C_2$ sind ein günstiges Paar von | + | *Die Folgen $C_1$ und $C_2$ sind ein günstiges Paar von M–Sequenzen gleicher Periodenlänge, zum Beispiel die PN–Generatoren mit den Oktalkennungen $(51)$ und $(75)$ vom Grad $G = 5$ und damit der Periodenlänge $P = 31$. |
| − | *Die | + | *Die Gold–Code–Familie besteht zum einen aus den M–Sequenzen $C_1$ und $C_2$ sowie aus einigen Modulo–2–Additionen dieser Folgen. Dabei wird $C_1$ mit fester Phase (gekennzeichnet durch die Vorbelegung aller Speicherzellen mit Einsen) verwendet, während für die Folge $C_2$ alle $P$ möglichen Anfangsphasen zulässig sind (alle Vorbelegungen außer der Nullbelegung). |
| − | *Verwendet man eine solche Codefamilie für CDMA, so stehen insgesamt $K_{\rm GCF} = P + 2 = 2^G + 1$ Folgen zur Verfügung. Die PAKF dieser Folgen ist nun aber nicht mehr zweiwertig wie die beiden PN–Sequenzen (+1 bzw. | + | *Verwendet man eine solche Codefamilie für CDMA, so stehen insgesamt $K_{\rm GCF} = P + 2 = 2^G + 1$ Folgen zur Verfügung. Die PAKF dieser Folgen ist nun aber nicht mehr zweiwertig wie die beiden PN–Sequenzen $(+1$ bzw. $-1/31)$, sondern vierwertig $(+1$, $+7/31$, $-1/31$, $-9/31)$. Durch die Phase von $C_2$ ändert sich zwar der spezifische Verlauf, aber nicht die möglichen PAKF–Werte. |
| − | Gold–Codes werden zum Beispiel bei UMTS zur Verwürfelung herangezogen, wie im Kapitel | + | Gold–Codes werden zum Beispiel bei UMTS zur Verwürfelung herangezogen, wie im Kapitel [[Beispiele_von_Nachrichtensystemen/Nachrichtentechnische_Aspekte_von_UMTS#Spreizcodes_und_Verw.C3.BCrfelung_bei_UMTS|Spreizcodes und Verwürfelung in UMTS]] des Buches „Beispiele von Nachrichtensystemen” ausgeführt ist. |
| + | *Die beiden Muttercode–Schieberegister sind dabei jeweils mit $G = 18$ Speicherzellen aufgebaut. | ||
| + | *Damit ergibt sich die Periodenlänge $P = 262\hspace{0.05cm} 143$. | ||
==Walsh–Funktionen== | ==Walsh–Funktionen== | ||
| − | Spreizfolgen mit sehr günstigen PKKF–Eigenschaften sind die so genannten Walsh–Funktionen, deren Konstruktion auf der Hadamard–Matrix basiert und durch Rekursion in einfacher Weise durchführbar ist. Ausgehend von der Matrix $\mathbf H_2$ können weitere Hadamard–Matrizen $\mathbf H_{2J}$ wie folgt generiert werden: | + | <br> |
| − | $${\mathbf{H}_{2}} = \left[ \begin{array}{ccc} +1 & +1 \\ +1 & -1 \end{array} \right] \hspace{0. | + | Spreizfolgen mit sehr günstigen PKKF–Eigenschaften sind die so genannten '''Walsh–Funktionen''', deren Konstruktion auf der '''Hadamard–Matrix''' basiert und durch Rekursion in einfacher Weise durchführbar ist. Ausgehend von der Matrix $\mathbf H_2$ können weitere Hadamard–Matrizen $\mathbf H_{2J}$ wie folgt generiert werden: |
| + | [[Datei:P_ID1882__Mod_T_5_3_S7_neu.png|right|frame| Walsh–Spreizfolgen $(J = 8)$ und Hadamard–Matrix $\mathbf H_8$ ]] | ||
| + | :$${\mathbf{H}_{2}} = \left[ \begin{array}{ccc} +1 & +1 \\ +1 & -1 \end{array} \right] \hspace{0.5cm} \Rightarrow \hspace{0.5cm}{\mathbf{H}_{2J}} = \left[ \begin{array}{ccc} \mathbf{H}_J & \mathbf{H}_J \\ \mathbf{H}_J & -\mathbf{H}_J \end{array} \right] $$ | ||
| + | :$$\hspace{0.5cm} \Rightarrow \hspace{0.5cm} | ||
{\mathbf{H}_{4}} = \left[ \begin{array}{cccc} +1 & +1 & +1 & +1 \\ +1 & -1 & +1 & -1 \\ | {\mathbf{H}_{4}} = \left[ \begin{array}{cccc} +1 & +1 & +1 & +1 \\ +1 & -1 & +1 & -1 \\ | ||
+1 & +1 & -1 & -1 \\+1 & -1 & -1 & +1 \end{array} \right] .$$ | +1 & +1 & -1 & -1 \\+1 & -1 & -1 & +1 \end{array} \right] .$$ | ||
| − | Die $J$ Zeilen einer solchen Matrix beschreiben die $J$ möglichen Spreizfolgen (jeweils der Länge $J$ | + | Die $J$ Zeilen einer solchen Matrix beschreiben die $J$ möglichen Spreizfolgen $($jeweils der Länge $J)$, die mit $w_0(t)$ bis $w_{J–1}(t)$ durchnummeriert werden. |
| + | |||
| + | Die Grafik zeigt die Hadamard–Matrix $\mathbf H_8$ (rechts) und die damit $J -1$ konstruierbaren Spreizfolgen. | ||
| + | *$J - 1$ deshalb, da die ungespreizte Folge $w_0(t)$ meist nicht verwendet wird. | ||
| + | *Beachten Sie bitte in der Grafik die farbliche Zuordnung zwischen den Zeilen der Hadamard–Matrix und den Spreizfolgen $w_j(t)$. Die Matrix $\mathbf H_4$ ist gelb hinterlegt. | ||
| + | *Die Animation [[Applets:Zur_Erzeugung_von_Walsh-Funktionen_(neues_Applet)|Zur Erzeugung von Walsh–Funktionen]] zeigt den Konstruktionsalgorithmus solcher Folgen. | ||
| + | |||
| + | Weiter gilt: | ||
| + | # Nimmt man zwei beliebige Zeilen und bildet die Korrelation (Mittelung über die Produkte), so ergibt sich stets der PKKF–Wert Null. Somit sind Walsh–Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA–System aufgrund ihrer Orthogonalität optimale Spreizfolgen. | ||
| + | # Bei asynchronem Betrieb (Beispiel: Uplink eines Mobilfunksystems) oder De–Orthogonalisierung aufgrund von Mehrwegeausbreitung sind dagegen Walsh–Funktionen allein zur Bandspreizung nicht unbedingt geeignet – siehe [[Aufgaben:5.4_Walsh–Funktionen_(PKKF,_PAKF)|Aufgabe 5.4]]. | ||
| + | # Hinsichtlich PAKF (periodische AKF) sind diese Folgen weniger gut: Jede einzelne Walsh–Funktion hat eine andere PAKF und jede einzelne PAKF ist ungünstiger als bei einer vergleichbaren PN–Sequenz. Das bedeutet: Die Synchronisierung ist bei Walsh–Funktionen schwieriger als mit PN–Sequenzen. | ||
| − | [[ | + | ==Codes mit variablem Spreizfaktor (OVSF–Code)== |
| + | <br> | ||
| + | Das 3G–Mobilfunksystem [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_UMTS|UMTS]] stellt verschiedene Datenraten zur Verfügung. Hierzu werden | ||
| + | *Spreizfolgen mit unterschiedlichen Spreizfaktoren $J = 4$ bis $J = 512$ benötigt, | ||
| + | *die alle zueinander orthogonal sein müssen. | ||
| + | [[Datei:P_ID1883__Mod_T_5_3_S8_neu.png|right|frame | Baumdiagramm zur Erzeugung eines OVSF–Codes]] | ||
| + | <br>Die so genannten '''OVSF–Codes''' ("Orthogonal Variable Spreading Factor") können mit Hilfe eines Codebaumes erstellt werden. Dabei entstehen bei jeder Verzweigung aus einem Code $C$ zwei neue Codes $(+C \ +\hspace{-0.05cm}C)$ und $(+C \ -\hspace{-0.05cm}C)$, wie in der Grafik oben rechts angedeutet ist. | ||
| − | + | Anzumerken ist, dass kein Vorgänger und Nachfolger eines Codes von anderen Teilnehmern benutzt werden darf. Im Beispiel könnte demnach unter Anderem folgende Auswahl getroffen werden: | |
| − | * | + | *acht Codes mit dem Spreizfaktor $J = 8$, oder |
| − | * | + | *die vier hinterlegten Codes – einmal mit $J = 2$, einmal mit $J = 4$ und zweimal mit $J = 8$. |
| − | |||
| − | + | ||
| − | + | Im zweiten Fall können die weiteren sechs Codes mit $J = 8$ nicht verwendet werden, da sie entweder mit „$+1 \ +\hspace{-0.05cm}1$” oder mit „$+1 \ -\hspace{-0.05cm}1 \ +\hspace{-0.05cm}1 \ -\hspace{-0.05cm}1$” beginnen. | |
| − | + | <br clear=all> | |
| − | * | + | Aus den vier zugehörigen Spreizfolgen in der Grafik rechts unten erkennt man, dass bei konstanter Chipdauer $T_c$ der Nutzer mit dem Spreizfaktor $J = 2$ mit höherer Datenrate übertragen kann als die Teilnehmer mit $J = 4$ bzw. $J = 8$, da seine Bitdauer $T_{\rm B}$ kleiner ist. |
| + | |||
| + | Aus der Grafik erkennt man weiter, dass die periodische KKF an der Stelle $τ = 0$ stets Null ist. | ||
| + | *Das heißt: Bildet man das Produkt von zwei beliebigen dieser Folgen und integriert man über den dargestellten Zeitbereich, so ergibt sich stets der Wert $0$. | ||
| + | *Das bedeutet auch: Ein OVSF–Code ist orthogonal zu allen anderen OVSF–Codes der gleichen Familie, solange es nicht zu Verschiebungen kommt. | ||
| − | + | Hinweis: Das SWF–Applet [[Applets:OVSF-Codes_(Applet)|OVSF–Codes]] zeigt den Konstruktionsalgorithmus dieser Codes und die zulässige Auswahl der Spreizfolgen. | |
| − | + | ==Aufgaben zum Kapitel== | |
| + | <br> | ||
| + | [[Aufgaben: 5.3 PAKF von PN–Sequenzen|Aufgabe 5.3: PAKF von PN–Sequenzen]] | ||
| − | + | [[Aufgaben:5.3Z Realisierung einer PN–Sequenz|Aufgabe 5.3Z: Realisierung einer PN–Sequenz]] | |
| − | |||
| − | |||
| + | [[Aufgaben: 5.4 Walsh–Funktionen (PKKF, PAKF)|Aufgabe 5.4: Walsh–Funktionen (PKKF, PAKF)]] | ||
| − | + | [[Aufgaben:5.4Z OVSF–Codes|Aufgabe 5.4Z: OVSF–Codes]] | |
| − | |||
| − | |||
==Quellenverzeichnis== | ==Quellenverzeichnis== | ||
Aktuelle Version vom 13. Dezember 2021, 12:12 Uhr
Inhaltsverzeichnis
- 1 Eigenschaften der Korrelationsfunktionen
- 2 Periodische AKF und KKF
- 3 Beurteilungskriterien für PN–Spreizfolgen
- 4 Pseudo–Noise–Folgen maximaler Länge
- 5 Codefamilien mit M–Sequenzen
- 6 Gold–Codes
- 7 Walsh–Funktionen
- 8 Codes mit variablem Spreizfaktor (OVSF–Code)
- 9 Aufgaben zum Kapitel
- 10 Quellenverzeichnis
Eigenschaften der Korrelationsfunktionen
Wichtige Beurteilungskriterien für Spreizfolgen sind die Korrelationsfunktionen.
$\text{Definition:}$ Betrachtet man zwei ergodische Prozesse mit den Musterfunktionen $x(t)$ und $y(t)$, so gilt für die Kreuzkorrelationsfunktion $\rm (KKF)$ der Prozesse:
- $$\varphi_{xy}(\tau)=\overline{x(t)\cdot y(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot y(t+\tau)\,\,\rm d \it t.$$
Die überstreichende Linie kennzeichnet hierbei eine Zeitmittelung.
$φ_{xy}(τ)$ ist ein quantitatives Maß für die lineare statistische Abhängigkeit der Augenblickswerte von Musterfunktionen $x(t)$ und $y(t + τ)$ der beiden Zufallsprozesse und dient somit der Beschreibung der statistischen Verwandtschaft zwischen diesen. Es gilt:
- Sind $x(t)$ und $y(t)$ unkorreliert, so ist $φ_{xy}(τ) \equiv 0$ $($also für alle beliebigen Werte von $τ)$.
- Im allgemeinen ist $φ_{xy}(τ)$ nicht symmetrisch, sondern das KKF–Maximum kann auch durchaus bei $τ_{\rm max} ≠ 0$ auftreten.
- Dann ergibt sich die maximale Korrelation durch eine gegenseitige Verschiebung der beiden betrachteten Signale um die Zeit $τ_{\rm max}$.
$\text{Definition:}$ Setzt man in obiger Gleichung $y(t) = x(t)$, so kommt man zur Autokorrelationsfunktion $\rm (AKF)$
- $$ \varphi_{xx}(\tau)=\overline{x(t)\cdot x(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot x(t+\tau)\,\,\rm d \it t$$
mit folgenden Eigenschaften:
- Die AKF ist ein Maß für die inneren statistischen Bindungen eines durch die Musterfunktion $x(t)$ festgelegten stationären und ergodischen Prozesses.
- Ist $x(t)$ reell, so ist $φ_{xx}(τ)$ eine reelle gerade Funktion: $φ_{xx}(–τ) = φ_{xx}(τ)$. Phasenbeziehungen gehen also in der AKF verloren.
- Beschreibt $x(t)$ einen komplexen Prozesse, so ist auch die AKF komplex.
- Der Maximalwert der AKF liegt bei $τ =0$. Es gilt stets $\vert φ_{xx}(τ)\vert ≤ φ_{xx}(τ = 0)$, wobei $φ_{xx}(τ =0)$ die Signalleistung $P_x = {\rm E}\big[x^2(t)\big]$ angibt.
- Der Gleichanteil von $x(t)$ kann aus dem Grenzwert für $τ → ∞$ ermittelt werden, so lange $x(t)$ keine periodischen Anteile beinhaltet:
- $$\overline{ x(t)} = {\rm E}\big[x(t)\big] = \sqrt{\lim_{\tau\to\infty}\,\varphi_{xx} (\tau)} \hspace{0.05cm}.$$
Autokorrelationsfunktion und Kreuzkorrelationsfunktion beschreiben die inneren Bindungen bzw. die gegenseitigen statistischen Abhängigkeiten im Zeitbereich. Die entsprechenden Beschreibungsfunktionen im Frequenzbereich sind
- das Leistungsdichtespektrum ${\it Φ}_{xx}(f)$, sowie
- das Kreuzleistungsdichtespektrum ${\it Φ}_{xy}(f)$.
Bei ergodischen Prozessen ergeben sich diese als die Fouriertransformierten von AKF und KKF:
- $${\it \Phi}_{xx}(f) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm}\varphi_{xx}(\tau)\hspace{0.05cm} ,\hspace{0.3cm} {\it \Phi}_{xy}(f) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm}\varphi_{xy}(\tau)\hspace{0.05cm}.$$
Hinweis: Im Folgenden schreiben wir wie im Buch Stochastische Signaltheorie vereinfachend
- für die AKF $φ_x(τ)$ anstelle von $φ_{xx}(τ)$,
- für das LDS ${\it Φ}_x(f)$ statt ${\it Φ}_{xx}(f)$.
Periodische AKF und KKF
Bei periodischen Signalen kann auf den Grenzübergang bei der AKF– und der KKF–Berechnung verzichtet werden, und man erhält mit der Periodendauer $T_0$ (diese muss für beide Signale gleich sein):
- $$\begin{align*}\varphi_{x}(\tau) & = \frac{1}{T_{\rm 0}}\cdot\int^{T_0}_{0}x(t)\cdot x(t+\tau)\,\,\rm d \it t\hspace{0.05cm} ,\\ \varphi_{xy}(\tau) & = \frac{1}{T_{\rm 0}}\cdot\int^{T_0}_{0}x(t)\cdot y(t+\tau)\,\,\rm d \it t\hspace{0.05cm}.\end{align*}$$
In diesem Fall ist die AKF ebenfalls eine periodische Funktion, und man spricht von der "periodischen Autokorrelationsfunktion" $\rm (PAKF)$. Diese zeigt folgende Einenschaft:
- $$\varphi_{x}(\pm T_0) = \varphi_{x}(\pm 2T_0) =\text{ ...} = \varphi_{x}(0) \hspace{0.05cm}.$$
Wir wenden nun obige Berechnungsvorschrift auf das Spreizsignal
- $$ c(t) = \sum\limits^{+\infty}_{\nu = -\infty}c_\nu\cdot g_c(t - \nu \cdot T_c)$$
an, wobei ein Rechteckimpuls $g_c(t)$ der Breite $T_c$ vorausgesetzt wird; $T_c$ nennt man die „Chipdauer”.
Berücksichtigt man die Periodizität $(T_0 = P · T_c)$ der Koeffizienten $c_ν ∈ \{±1\}$, so ergeben sich die diskreten AKF–Werte bei Vielfachen $($Parameter $λ)$ von $T_c$:
- $$\varphi_{c}(\lambda \cdot T_c) = \frac{1}{P}\cdot\sum\limits^{P-1}_{\nu = 0} c_\nu \cdot c_{\nu+ {\it \lambda} }\hspace{0.05cm}.$$
- Der maximale PAKF–Wert ergibt sich für $λ = 0$ und für Vielfache der Periodenlänge $P$.
- Aufgrund des rechteckförmigen Impulses $g_c(t)$ ist der PAKF–Verlauf zwischen zwei Abtastwerten $λ · T_c$ und $(λ + 1) · T_c$ stets linear.
Entsprechend ist die "periodische Kreuzkorrelationsfunktion" $\rm (PKKF)$ zwischen den zwei Spreizfolgen $〈c_ν〉$ und $〈c\hspace{0.04cm}'_ν〉$ gleicher Periodenlänge $P$ wie folgt gegeben:
- $$\varphi_{cc\hspace{0.04cm}'}(\lambda \cdot T_c) = \frac{1}{P}\cdot\sum\limits^{P-1}_{\nu = 0} c_\nu \cdot c\hspace{0.04cm}'_{\nu+ \lambda }\hspace{0.05cm}.$$
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 9: Stochastische Prozesse, Programm „stp”
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms und
- der Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; Kapitel 9: Seite 207-228.
Beurteilungskriterien für PN–Spreizfolgen
Die Qualität eines auf PN–Modulation basierenden CDMA–Systems hängt signifikant von den PAKF– und PKKF–Eigenschaften der verwendeten Spreizfolgen ab. Zusammenfassend kann man sagen:
- Die PAKF der verwendeten Spreizcodeklasse sollte möglichst durch einen ausgeprägten Peak bei ${\it λ} = 0$ gekennzeichnet sein, um die Synchronisation beim Empfänger einfach gestalten zu können. Bei Mehrwegeempfang mit einem Echo der Laufzeitdifferenz $λ · T_c$ ist zudem die Degradation aufgrund von Impulsinterferenzen um so geringer, je kleiner $|φ_c(λ · T_c)|$ ist.
- Der störende Einfluss interferierender CDMA–Teilnehmer lässt sich durch den PKKF–Wert $φ_{cc\hspace{0.04cm}'} (λ = 0)$ abschätzen. Ist dieser gleich Null, so spricht man von orthogonalen Funktionen. Die Fehlerwahrscheinlichkeit wird in diesem Fall nicht erhöht. Sind alle Spreizfolgen orthogonal, so ergibt sich auch bei $J$ Teilnehmern die gleiche Fehlerwahrscheinlichkeit wie bei nur einem einzigen Nutzer.
- Diese letzte Aussage ist in synchronen Systemen mit verzerrungsfreiem Kanal (zum Beispiel bei AWGN) von besonderer Bedeutung. Bei asynchronem Betrieb oder Mehrwegeempfang kommt es dagegen zu einer "De–Orthogonalisierung" und der strengeren Forderung, dass die PKKF zwischen den einzelnen Folgen zu allen Zeitpunkten (betragsmäßig) möglichst kleine Werte annehmen soll.
Bei der Auswahl von Codefamilien für ein CDMA–System ist weiter darauf zu achten, dass man bei gegebenem Spreizgrad $J = P$ möglichst viele Codefolgen mit günstigen Eigenschaften hinsichtlich dieser drei Kriterien finden kann, um somit auch möglichst viele Teilnehmer gleichzeitig im gleichen Frequenzband versorgen zu können.
Pseudo–Noise–Folgen maximaler Länge
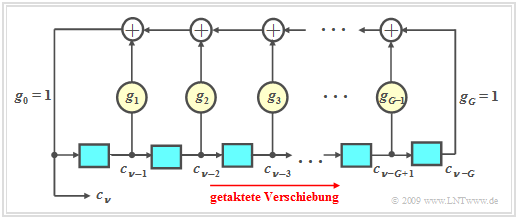
Mit einem rückgekoppelten Schieberegister lässt sich eine Folge mit günstigen AKF–Eigenschaften erzeugen, wenn man die Rückführungskoeffizienten $g_i$ mit Index $i = 1, \text{...} \ , G-1$ geeignet wählt.
- Die Folge $〈c_ν〉$ ist im strengen Sinne nicht zufällig, sondern periodisch.
- Aufgrund der großen Periodenlänge $P$ erscheint sie aber für einen unbedarften Betrachter als stochastisch.
- Man spricht von einer Pseudo–Noise–Folge oder kurz "PN–Folge".
$\text{PN–Generatoren}$ haben folgende Eigenschaften, siehe Kapitel Erzeugung von diskreten Zufallsgrößen im Buch „Stochastische Signaltheorie”:
- Die zu früheren Zeitpunkten generierten Binärwerte $c_{ν-1}, \text{...} \ , c_{ν-G}$ sind in den $G$ Speicherzellen des Schieberegisters abgelegt. Man bezeichnet $G$ als den Grad des Schieberegisters.
- Die Koeffizienten $g_1, \ \text{...} \ , g_{G-1}$ sind Binärwerte. Eine „1” kennzeichnet eine Rückführung an der entsprechenden Stelle des Schieberegisters und eine „0” keine Rückführung.
- Für das aktuell erzeugte Symbol gilt mit $g_i ∈ \{0, 1\}$ und $i = 1,\ \text{...}\ , G-1$:
- $$c_\nu = (g_1\cdot c_{\nu-1}+g_2\cdot c_{\nu-2}+\ \text{...}\ +g_i\cdot c_{\nu-i}+\ \text{...}\ +g_{G-1}\cdot c_{\nu-G+1}+ c_{\nu-G})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$
- Die Modulo–2–Addition kann zum Beispiel durch eine $\rm XOR$–Verknüpfung realisiert werden:
- $$(x + y)\hspace{0.2cm} \rm mod\hspace{0.2cm}2 = {\it x}\hspace{0.2cm}\rm XOR\hspace{0.2cm} {\it y} = \left\{ \begin{array}{*{2}{c}} 0 & \rm falls\hspace{0.1cm} {\it x}= {\it y},\\ 1 & \rm falls\hspace{0.1cm} {\it x}\neq {\it y}. \\ \end{array} \right.$$
- Sind nicht alle $G$ Speicherzellen mit Nullen vorbelegt, so entsteht eine periodische Zufallsfolge $〈c_ν〉$. Die Periodenlänge $P$ dieser Folge hängt stark von den Rückkopplungskoeffizienten $g_i$ ab.
- Für jeden Grad $G$ gibt es zumindest zwei Konfigurationen mit der hierfür maximalen Periode $P_{\rm max} = 2^G – 1$.
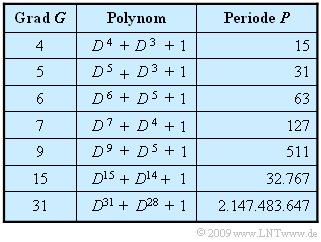
In der Tabelle sind für einige Werte von $G$ das Generatorpolynom $G(D)$ einer solchen M–Sequenz und die zugehörige (maximale) Periodenlänge $P$ angegeben, wobei das „M” für „Maximal” steht. Nachfolgend werden die hier gemachten Aussagen am Beispiel $G = 4$ verdeutlicht.
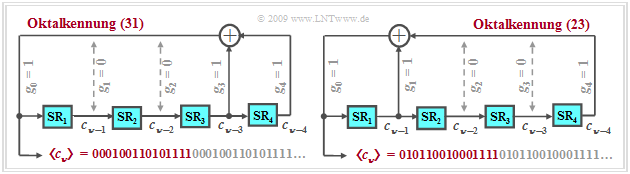
$\text{Beispiel 1:}$ Die Grafik zeigt zwei mögliche Anordnungen zur Erzeugung einer PN–Folge maximaler Länge für $G = 4$ ⇒ $P = 15$.
- Als Kurzbezeichnung wird meist die Oktaldarstellung der Binärzahl $(g_G, \ \text{...} \ ,g_2, g_1, g_0)$ gewählt. Grundsätzlich ist $g_0 = g_G = 1$ zu setzen.
- Die linke Konfiguration wird mit $\rm (11001)_{binär} = (31)_{oktal}$ bezeichnet, das dazugehörige Generatorpolynom lautet:
- $$G_1(D) = D^4 + D^3 +1\hspace{0.05cm}.$$
- Die rechte Anordnung mit $\rm (10011)_{binär} = (23)_{oktal}$ ist dagegen durch folgendes Polynom beschreibbar:
- $$G_{\rm 2}(D) =D^4 + D +1 \hspace{0.05cm}.$$
- Das Polynom $G_2(D)$ ist reziprok zu $G_{\rm 1}(D)$:
- $$G_{\rm 2}(D) = D^4 \cdot (D^{-4} + D^{-3} +1) =D^4 + D +1 \hspace{0.05cm}.$$
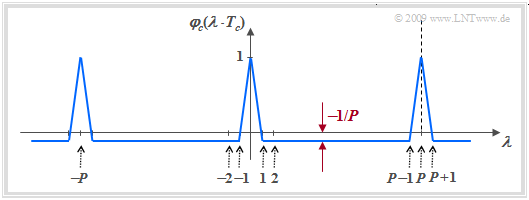
Da sowohl $G_1(D)$ als auch $G_{\rm 2}(D)$ primitive Generatorpolynome darstellen (der Nachweis hierfür ist nicht einfach), haben beide Ausgangsfolgen die für $G = 4$ maximale Periodenlänge $P = 15$. Wie in der Aufgabe 5.3 gezeigt wird, ergibt sich die PAKF in der unipolaren Darstellung ⇒ $c_ν ∈ \{0, 1\}$ zu
- $${\it \varphi}_{c{\rm ,\hspace{0.05cm}unipolar} }(\lambda \cdot T_c) = \left\{ \begin{array}{c}(P+1)/(2P) \\ (P+1)/(4P) \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r} } \\ {\rm{sonst} } \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} \lambda = 0, \pm P, \pm 2P, \text{...} \hspace{0.05cm} \\ \\ \end{array}$$
Nach Umsetzung in bipolare Koeffizienten $($das heißt: $0 \ ⇒ +1$, $1 \ ⇒ -1)$ erhält man:
- $${\it \varphi}_{c{\rm ,\hspace{0.05cm}bipolar} }(\lambda \cdot T_c) = \left\{ \begin{array}{c}1 \\ -P \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r} } \\ {\rm{sonst.} } \hspace{0.05cm} \\ \end{array}\begin{array}{*{20}c} \lambda = 0, \pm P, \pm 2P, \text{...} \hspace{0.05cm} \\ \\ \end{array}$$
- Man erkennt aus der unteren Skizze die gewünschten ausgeprägten PAKF–Peaks in Abständen der Periode $P$.
- Weniger gut sind die PAKF–Eigenschaften der PN–Sequenzen, wie im Kapitel Fehlerwahrscheinlichkeit der PN–Modulation gezeigt werden wird.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 2: Pseudonoise–Generatoren, Programm „png”
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms und
- der Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; Kapitel 2: Seite 23-32.
Codefamilien mit M–Sequenzen
Bei CDMA wird für jeden Teilnehmer eine spezifische Spreizfolge gleicher Periodenlänge benötigt. Als Codefamilie bezeichnet man eine (möglichst große) Menge an Spreizsequenzen gleicher Periodenlänge $P$, gültig jeweils für einen Registergrad $G$.
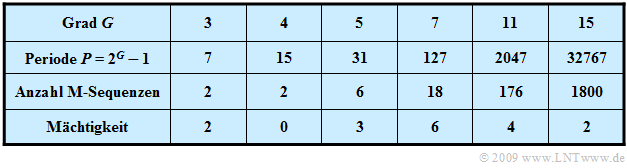
Die Tabelle zeigt, dass die Anzahl von PN–Sequenzen maximaler Länge sehr gering ist. Für den Grad $G = 5$ ⇒ $P = 31$ gibt es zum Beispiel gerade einmal sechs M–Sequenzen, nämlich die PN–Generatoren mit den Oktalkennungen $(45),\ (51),\ (57),\ (67),\ (73)$ und $(75)$.
Des Weiteren ist in der Literatur auch der Begriff Mächtigkeit der Codefamilie zu finden.
- Diese Größe gibt an, wie viele M–Sequenzen und damit gleichzeitige CDMA–Teilnehmer möglich sind, wenn man fordert, dass alle Codepaare „günstige PKKF–Eigenschaften” aufweisen.
- Aus Platzgründen kann hier nicht explizit ausgeführt werden, was man unter „günstig” genau zu verstehen hat. Hierzu sei auf die Originalliteratur verwiesen, zum Beispiel [ZP85][1].
Die letzte Zeile in obiger Tabelle macht deutlich, dass die Mächtigkeit von M–Sequenz–Codefamilien äußerst beschränkt ist, auch bei großem $G$ und damit großer Periodenlänge $P$.
Ist $G$ ein Vielfaches von $4$ ⇒ $P = 15$, $P = 255$, $P = 4095$ usw., so gibt es grundsätzlich keine günstigen Paare.
Gold–Codes
Um größere Codefamilien zu erhalten als mit M–Sequenzen, müssen die Anforderungen an die periodische Kreuzkorrelationsfunktion $\rm (PKKF)$ abgeschwächt werden. Mit dieser Einschränkung erhält man Codefamilien mit einer weitaus größeren Mächtigkeit, so dass auch mehr CDMA–Teilnehmer versorgt werden können.
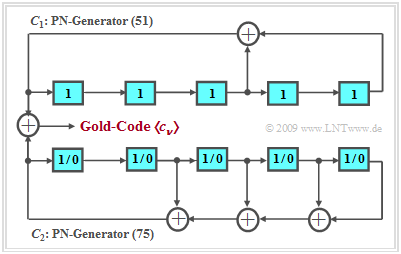
Gold–Codes verwenden dieses Prinzip. Die Vorschrift zur Erzeugung einer Gold–Code–Familie $\rm (GCF)$ lautet, wobei ein „+” eine Modulo–2–Addition bezeichnet:
- $${\rm GCF}(C_1, C_2) = \{ C_1, C_2, C_1 + C_2, C_1 + D \cdot C_2, C_1 + D^2 \cdot C_2, \ \text{...} \ , C_1 + D^{P-1} \cdot C_2 \} \hspace{0.05cm}.$$
Das Prinzip ist in der Grafik an einem Beispiel dargestellt:
- Die Folgen $C_1$ und $C_2$ sind ein günstiges Paar von M–Sequenzen gleicher Periodenlänge, zum Beispiel die PN–Generatoren mit den Oktalkennungen $(51)$ und $(75)$ vom Grad $G = 5$ und damit der Periodenlänge $P = 31$.
- Die Gold–Code–Familie besteht zum einen aus den M–Sequenzen $C_1$ und $C_2$ sowie aus einigen Modulo–2–Additionen dieser Folgen. Dabei wird $C_1$ mit fester Phase (gekennzeichnet durch die Vorbelegung aller Speicherzellen mit Einsen) verwendet, während für die Folge $C_2$ alle $P$ möglichen Anfangsphasen zulässig sind (alle Vorbelegungen außer der Nullbelegung).
- Verwendet man eine solche Codefamilie für CDMA, so stehen insgesamt $K_{\rm GCF} = P + 2 = 2^G + 1$ Folgen zur Verfügung. Die PAKF dieser Folgen ist nun aber nicht mehr zweiwertig wie die beiden PN–Sequenzen $(+1$ bzw. $-1/31)$, sondern vierwertig $(+1$, $+7/31$, $-1/31$, $-9/31)$. Durch die Phase von $C_2$ ändert sich zwar der spezifische Verlauf, aber nicht die möglichen PAKF–Werte.
Gold–Codes werden zum Beispiel bei UMTS zur Verwürfelung herangezogen, wie im Kapitel Spreizcodes und Verwürfelung in UMTS des Buches „Beispiele von Nachrichtensystemen” ausgeführt ist.
- Die beiden Muttercode–Schieberegister sind dabei jeweils mit $G = 18$ Speicherzellen aufgebaut.
- Damit ergibt sich die Periodenlänge $P = 262\hspace{0.05cm} 143$.
Walsh–Funktionen
Spreizfolgen mit sehr günstigen PKKF–Eigenschaften sind die so genannten Walsh–Funktionen, deren Konstruktion auf der Hadamard–Matrix basiert und durch Rekursion in einfacher Weise durchführbar ist. Ausgehend von der Matrix $\mathbf H_2$ können weitere Hadamard–Matrizen $\mathbf H_{2J}$ wie folgt generiert werden:
- $${\mathbf{H}_{2}} = \left[ \begin{array}{ccc} +1 & +1 \\ +1 & -1 \end{array} \right] \hspace{0.5cm} \Rightarrow \hspace{0.5cm}{\mathbf{H}_{2J}} = \left[ \begin{array}{ccc} \mathbf{H}_J & \mathbf{H}_J \\ \mathbf{H}_J & -\mathbf{H}_J \end{array} \right] $$
- $$\hspace{0.5cm} \Rightarrow \hspace{0.5cm} {\mathbf{H}_{4}} = \left[ \begin{array}{cccc} +1 & +1 & +1 & +1 \\ +1 & -1 & +1 & -1 \\ +1 & +1 & -1 & -1 \\+1 & -1 & -1 & +1 \end{array} \right] .$$
Die $J$ Zeilen einer solchen Matrix beschreiben die $J$ möglichen Spreizfolgen $($jeweils der Länge $J)$, die mit $w_0(t)$ bis $w_{J–1}(t)$ durchnummeriert werden.
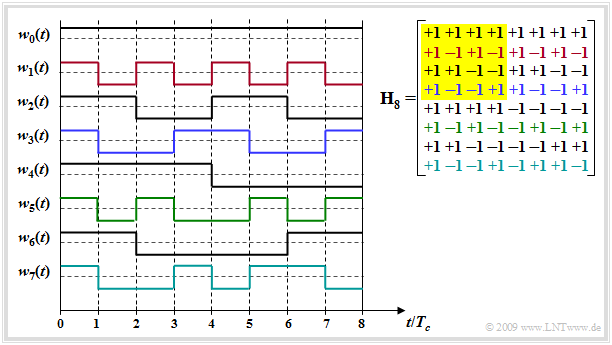
Die Grafik zeigt die Hadamard–Matrix $\mathbf H_8$ (rechts) und die damit $J -1$ konstruierbaren Spreizfolgen.
- $J - 1$ deshalb, da die ungespreizte Folge $w_0(t)$ meist nicht verwendet wird.
- Beachten Sie bitte in der Grafik die farbliche Zuordnung zwischen den Zeilen der Hadamard–Matrix und den Spreizfolgen $w_j(t)$. Die Matrix $\mathbf H_4$ ist gelb hinterlegt.
- Die Animation Zur Erzeugung von Walsh–Funktionen zeigt den Konstruktionsalgorithmus solcher Folgen.
Weiter gilt:
- Nimmt man zwei beliebige Zeilen und bildet die Korrelation (Mittelung über die Produkte), so ergibt sich stets der PKKF–Wert Null. Somit sind Walsh–Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA–System aufgrund ihrer Orthogonalität optimale Spreizfolgen.
- Bei asynchronem Betrieb (Beispiel: Uplink eines Mobilfunksystems) oder De–Orthogonalisierung aufgrund von Mehrwegeausbreitung sind dagegen Walsh–Funktionen allein zur Bandspreizung nicht unbedingt geeignet – siehe Aufgabe 5.4.
- Hinsichtlich PAKF (periodische AKF) sind diese Folgen weniger gut: Jede einzelne Walsh–Funktion hat eine andere PAKF und jede einzelne PAKF ist ungünstiger als bei einer vergleichbaren PN–Sequenz. Das bedeutet: Die Synchronisierung ist bei Walsh–Funktionen schwieriger als mit PN–Sequenzen.
Codes mit variablem Spreizfaktor (OVSF–Code)
Das 3G–Mobilfunksystem UMTS stellt verschiedene Datenraten zur Verfügung. Hierzu werden
- Spreizfolgen mit unterschiedlichen Spreizfaktoren $J = 4$ bis $J = 512$ benötigt,
- die alle zueinander orthogonal sein müssen.
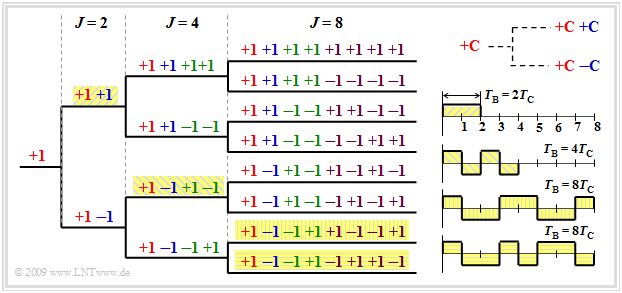
Die so genannten OVSF–Codes ("Orthogonal Variable Spreading Factor") können mit Hilfe eines Codebaumes erstellt werden. Dabei entstehen bei jeder Verzweigung aus einem Code $C$ zwei neue Codes $(+C \ +\hspace{-0.05cm}C)$ und $(+C \ -\hspace{-0.05cm}C)$, wie in der Grafik oben rechts angedeutet ist.
Anzumerken ist, dass kein Vorgänger und Nachfolger eines Codes von anderen Teilnehmern benutzt werden darf. Im Beispiel könnte demnach unter Anderem folgende Auswahl getroffen werden:
- acht Codes mit dem Spreizfaktor $J = 8$, oder
- die vier hinterlegten Codes – einmal mit $J = 2$, einmal mit $J = 4$ und zweimal mit $J = 8$.
Im zweiten Fall können die weiteren sechs Codes mit $J = 8$ nicht verwendet werden, da sie entweder mit „$+1 \ +\hspace{-0.05cm}1$” oder mit „$+1 \ -\hspace{-0.05cm}1 \ +\hspace{-0.05cm}1 \ -\hspace{-0.05cm}1$” beginnen.
Aus den vier zugehörigen Spreizfolgen in der Grafik rechts unten erkennt man, dass bei konstanter Chipdauer $T_c$ der Nutzer mit dem Spreizfaktor $J = 2$ mit höherer Datenrate übertragen kann als die Teilnehmer mit $J = 4$ bzw. $J = 8$, da seine Bitdauer $T_{\rm B}$ kleiner ist.
Aus der Grafik erkennt man weiter, dass die periodische KKF an der Stelle $τ = 0$ stets Null ist.
- Das heißt: Bildet man das Produkt von zwei beliebigen dieser Folgen und integriert man über den dargestellten Zeitbereich, so ergibt sich stets der Wert $0$.
- Das bedeutet auch: Ein OVSF–Code ist orthogonal zu allen anderen OVSF–Codes der gleichen Familie, solange es nicht zu Verschiebungen kommt.
Hinweis: Das SWF–Applet OVSF–Codes zeigt den Konstruktionsalgorithmus dieser Codes und die zulässige Auswahl der Spreizfolgen.
Aufgaben zum Kapitel
Aufgabe 5.3: PAKF von PN–Sequenzen
Aufgabe 5.3Z: Realisierung einer PN–Sequenz
Aufgabe 5.4: Walsh–Funktionen (PKKF, PAKF)
Quellenverzeichnis
- ↑ Ziemer, R.; Peterson, R. L.: Digital Communication and Spread Spectrum Systems. New York: McMillon, 1985.