Stochastische Signaltheorie/Verteilungsfunktion: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
==Zusammenhang zwischen WDF und VTF== | ==Zusammenhang zwischen WDF und VTF== | ||
<br> | <br> | ||
| − | Zur Beschreibung von Zufallsgrößen wird neben der [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion_(WDF)|Wahrscheinlichkeitsdichtefunktion]] (WDF) auch | + | Zur Beschreibung von Zufallsgrößen wird neben der [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion_(WDF)|Wahrscheinlichkeitsdichtefunktion]] $\rm (WDF)$ auch die Verteilungsfunktion $\rm (VTF)$ mit folgender Definition verwendet: |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Die '''Verteilungsfunktion''' $F_{x}(r)$ entspricht der Wahrscheinlichkeit, dass die Zufallsgröße $x$ kleiner oder gleich einem reellen Zahlenwert $r$ ist: |
| − | Die '''Verteilungsfunktion''' $F_{x}(r)$ entspricht der Wahrscheinlichkeit, dass die Zufallsgröße $x$ kleiner oder gleich einem reellen Zahlenwert $r$ ist: | ||
:$$F_{x}(r) = {\rm Pr}( x \le r).$$ | :$$F_{x}(r) = {\rm Pr}( x \le r).$$ | ||
| − | Die englische Bezeichnung für die Verteilungsfunktion (VTF) ist | + | Die englische Bezeichnung für die Verteilungsfunktion (VTF) ist "Cumulative Distribution Function" $\rm (CDF)$. }} |
Bei einer kontinuierlichen Zufallsgröße sind bezüglich der Verteilungsfunktion folgende Aussagen möglich: | Bei einer kontinuierlichen Zufallsgröße sind bezüglich der Verteilungsfunktion folgende Aussagen möglich: | ||
| − | *Die Verteilungsfunktion ist aus der Wahrscheinlichkeitsdichtefunktion $f_{x}(x)$ durch Integration berechenbar. Es gilt: | + | *Die Verteilungsfunktion ist aus der Wahrscheinlichkeitsdichtefunktion $f_{x}(x)$ durch Integration berechenbar. Es gilt: |
:$$F_{x}(r) = \int_{-\infty}^{r}f_x(x)\,{\rm d}x.$$ | :$$F_{x}(r) = \int_{-\infty}^{r}f_x(x)\,{\rm d}x.$$ | ||
| − | *Da die WDF nie negativ ist, steigt $F_{x}(r)$ zumindest schwach monoton an, und liegt stets zwischen den folgenden Grenzwerten | + | *Da die WDF nie negativ ist, steigt $F_{x}(r)$ zumindest schwach monoton an, und liegt stets zwischen den folgenden Grenzwerten: |
:$$F_{x}(r → \hspace{0.05cm} – \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{x}(r → +∞) = 1.$$ | :$$F_{x}(r → \hspace{0.05cm} – \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{x}(r → +∞) = 1.$$ | ||
*Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch Differentiation bestimmen: | *Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch Differentiation bestimmen: | ||
:$$f_{x}(x)=\frac{{\rm d} F_{x}(r)}{{\rm d} r}\Bigg |_{\hspace{0.1cm}r=x}.$$ | :$$f_{x}(x)=\frac{{\rm d} F_{x}(r)}{{\rm d} r}\Bigg |_{\hspace{0.1cm}r=x}.$$ | ||
| − | :Der Zusatz $ | + | :Der Zusatz „$r = x$” macht deutlich, dass bei unserer Nomenklatur das Argument der Wahrscheinlichkeitsdichtefunktion die Zufallsgröße selbst ist, während das VTF–Argument eine beliebige reelle Variable $r$ angibt. |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Hinweise zur Nomenklatur:}$ | ||
| + | |||
| + | Hätten wir bei den Definitionen von $\rm WDF$ und $\rm VTF$ | ||
| + | *zwischen der Zufallsgröße $X$ | ||
| + | *und den Realisierungen $x ∈ X$ unterschieden ⇒ $f_{X}(x), F_{X}(x)$, | ||
| − | + | so ergäbe sich folgende Nomenklatur: | |
| − | |||
| − | |||
:$$F_{X}(x) = {\rm Pr}(X \le x) = \int_{-\infty}^{x}f_{x}(\xi)\,{\rm d}\xi.$$ | :$$F_{X}(x) = {\rm Pr}(X \le x) = \int_{-\infty}^{x}f_{x}(\xi)\,{\rm d}\xi.$$ | ||
| − | Leider haben wir uns zu Beginn unseres | + | Leider haben wir uns zu Beginn unseres $\rm LNTwww$–Projektes (2001) aus durchaus berechtigten Gründen für unsere Nomenklatur entschieden, was nun (2017) nicht mehr zu ändern ist, auch im Hinblick auf die realisierten Lernvideos. |
| − | Wir bleiben also bei $f_{x}(x)$ anstelle von $f_{X}(x)$ sowie $F_{x}(r)$ anstelle von $F_{X}(x).$ | + | '''Wir bleiben also bei $f_{x}(x)$ anstelle von $f_{X}(x)$ sowie $F_{x}(r)$ anstelle von $F_{X}(x).$'''}} |
==Verteilungsfunktion bei kontinuierlichen Zufallsgrößen== | ==Verteilungsfunktion bei kontinuierlichen Zufallsgrößen== | ||
<br> | <br> | ||
| − | Die im letzten Abschnitt angegebenen Gleichungen gelten nur für wertkontinuierliche Zufallsgrößen und sollen hier durch ein Beispiel verdeutlicht werden. Im nächsten Abschnitt wird gezeigt, dass für [[Stochastische_Signaltheorie/Verteilungsfunktion#Verteilungsfunktion_bei_diskreten_Zufallsgr.C3.B6.C3.9Fen|diskrete Zufallsgrößen]] die Gleichungen etwas modifiziert werden müssen. | + | Die im letzten Abschnitt angegebenen Gleichungen gelten nur für wertkontinuierliche Zufallsgrößen und sollen hier durch ein Beispiel verdeutlicht werden. Im nächsten Abschnitt wird gezeigt, dass für [[Stochastische_Signaltheorie/Verteilungsfunktion#Verteilungsfunktion_bei_diskreten_Zufallsgr.C3.B6.C3.9Fen|diskrete Zufallsgrößen]] die Gleichungen etwas modifiziert werden müssen. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ | + | $\text{Beispiel 1:}$ Das linke Bild zeigt das Foto „Lena”, das häufig als Testvorlage für Bildcodierverfahren dient. |
| − | Das linke Bild zeigt das Foto | + | [[Datei:P_ID617__Sto_T_3_2_S1b_neu.png |right|frame| WDF und VTF eines wertkontinuierlichen Bildes]] |
| − | *Wird dieses Bild in 256 × 256 Bildpunkte (Pixel) unterteilt, und ermittelt man für jedes einzelne Pixel die Helligkeit, so erhält man eine Folge $〈x_ν〉$ von Grauwerten | + | *Wird dieses Bild in $256 × 256$ Bildpunkte (Pixel) unterteilt, und ermittelt man für jedes einzelne Pixel die Helligkeit, so erhält man eine Folge $〈x_ν〉$ von Grauwerten. Deren Länge ist $N = 256^2 = 65536$. |
| − | *Der Grauwert $x$ ist eine wertkontinuierliche Zufallsgröße, wobei die Zuordnung zu Zahlenwerten willkürlich ist. Zum Beispiel sei „Schwarz” durch den Wert $x = 0$ und „Weiß” durch $x = 1$ charakterisiert. Der Zahlenwert $x =0.5$ kennzeichnet dann eine mittlere Graufärbung. | + | *Der Grauwert $x$ ist eine wertkontinuierliche Zufallsgröße, wobei die Zuordnung zu Zahlenwerten willkürlich ist. Zum Beispiel sei „Schwarz” durch den Wert $x = 0$ und „Weiß” durch $x = 1$ charakterisiert. Der Zahlenwert $x =0.5$ kennzeichnet dann eine mittlere Graufärbung. |
| − | |||
| − | Im mittleren Bild ist die WDF $f_{x}(x)$ dargestellt, die in der Literatur auch oft als | + | Im mittleren Bild ist die WDF $f_{x}(x)$ dargestellt, die in der Literatur auch oft als „Grauwertstatistik” bezeichnet wird. |
| − | *Es ist ersichtlich, dass im Originalbild einige Grauwerte bevorzugt sind und die beiden Extremwerte $x =0$ („tiefes Schwarz”) bzw. $x =1$ („reines Weiß”) nur sehr selten auftreten. | + | *Es ist ersichtlich, dass im Originalbild einige Grauwerte bevorzugt sind und die beiden Extremwerte $x =0$ („tiefes Schwarz”) bzw. $x =1$ („reines Weiß”) nur sehr selten auftreten. |
| − | *Die Verteilungsfunktion $F_{ | + | *Die Verteilungsfunktion $F_{x}(r)$ dieser kontinuierlichen Zufallsgröße ist stetig und steigt, wie das rechte Bild zeigt, von $0$ auf $1$ monoton an. Bei $r \approx 0$ und $r \approx 1$ verläuft die VTF aufgrund fehlender WDF–Anteile horizontal. |
| − | + | Anmerkung: Genau genommen ist bei einem am Computer darstellbaren Bild – im Gegensatz zu einem „analogen” Foto – der Grauwert stets eine wertdiskrete Zufallsgröße. Bei großer Auflösung der Farbinformation („Farbtiefe”) kann man diese Zufallsgröße allerdings näherungsweise als wertkontinuierlich betrachten. }} | |
| − | Die in diesem Abschnitt behandelte Thematik ist im Lernvideo [[Zusammenhang_zwischen_WDF_und_VTF_(Lernvideo)|Zusammenhang zwischen WDF und VTF]] zusammengefasst. | + | Die in diesem Abschnitt behandelte Thematik ist im Lernvideo [[Zusammenhang_zwischen_WDF_und_VTF_(Lernvideo)|Zusammenhang zwischen WDF und VTF]] zusammengefasst. |
==Verteilungsfunktion bei diskreten Zufallsgrößen== | ==Verteilungsfunktion bei diskreten Zufallsgrößen== | ||
<br> | <br> | ||
| − | Für die Berechnung der Verteilungsfunktion einer wertdiskreten Zufallsgröße $x$ aus deren WDF muss stets von einer allgemeineren Gleichung ausgegangen werden. Hier gilt mit mit der Hilfsvariablen $\varepsilon > 0$: | + | Für die Berechnung der Verteilungsfunktion einer wertdiskreten Zufallsgröße $x$ aus deren WDF muss stets von einer allgemeineren Gleichung ausgegangen werden. Hier gilt mit mit der Hilfsvariablen $\varepsilon > 0$: |
:$$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm}0}\int_{-\infty}^{r+\varepsilon}f_x(x)\,{\rm d}x.$$ | :$$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm}0}\int_{-\infty}^{r+\varepsilon}f_x(x)\,{\rm d}x.$$ | ||
| − | *Die Berechnung der Verteilungsfunktion durch Grenzwertbildung ist aufgrund des | + | *Die Berechnung der Verteilungsfunktion durch Grenzwertbildung ist aufgrund des „Kleiner/Gleich”–Zeichens in der [[Stochastische_Signaltheorie/Verteilungsfunktion#Zusammenhang_zwischen_WDF_und_VTF|allgemeinen Definition]] erforderlich. |
| − | *Berücksichtigt man zudem, dass bei einer diskreten Zufallsgröße die WDF aus einer Summe gewichteter [[Signaldarstellung/Allgemeine_Beschreibung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals#Diracfunktion_im_Frequenzbereich|Diracfunktionen]] besteht, so erhält man: | + | *Berücksichtigt man zudem, dass bei einer diskreten Zufallsgröße die WDF aus einer Summe gewichteter [[Signaldarstellung/Allgemeine_Beschreibung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals#Diracfunktion_im_Frequenzbereich|Diracfunktionen]] besteht, so erhält man: |
:$$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{r+\varepsilon}\sum\limits_{\mu= 1}^{ M}p_\mu\cdot \delta(x-x_\mu)\,{\rm d}x.$$ | :$$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{r+\varepsilon}\sum\limits_{\mu= 1}^{ M}p_\mu\cdot \delta(x-x_\mu)\,{\rm d}x.$$ | ||
| − | *Vertauscht man in | + | *Vertauscht man in der Gleichung Integration und Summation, und berücksichtigt, dass die Integration über die Diracfunktion die Sprungfunktion ergibt, so erhält man: |
:$$F_{x}(r)=\sum\limits_{\mu= \rm 1}^{\it M}p_\mu\cdot \gamma_0 (r-x_\mu),\hspace{0.4cm}{\rm mit} \hspace{0.4cm}\gamma_0(x)=\lim_{\epsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{x+\varepsilon}\delta (u)\,{\rm d} u = \left\{ \begin{array}{*{2}{c}} 0 \hspace{0.4cm} {\rm falls}\hspace{0.1cm} x< 0,\\ 1 \hspace{0.4cm} {\rm falls}\hspace{0.1cm}x\ge 0. \\ \end{array} \right.$$ | :$$F_{x}(r)=\sum\limits_{\mu= \rm 1}^{\it M}p_\mu\cdot \gamma_0 (r-x_\mu),\hspace{0.4cm}{\rm mit} \hspace{0.4cm}\gamma_0(x)=\lim_{\epsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{x+\varepsilon}\delta (u)\,{\rm d} u = \left\{ \begin{array}{*{2}{c}} 0 \hspace{0.4cm} {\rm falls}\hspace{0.1cm} x< 0,\\ 1 \hspace{0.4cm} {\rm falls}\hspace{0.1cm}x\ge 0. \\ \end{array} \right.$$ | ||
Hierzu ist anzumerken: | Hierzu ist anzumerken: | ||
| − | * $γ_0(x)$ unterscheidet sich von der in der Systemtheorie üblichen [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Zuordnungssatz|Sprungfunktion]] $γ(x)$ dadurch, dass an der Sprungstelle $x = 0$ der rechtsseitige Grenzwert „Eins” gültig ist (anstelle des Mittelwertes „ | + | * Die Funktion $γ_0(x)$ unterscheidet sich von der in der Systemtheorie üblichen [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Zuordnungssatz|Sprungfunktion]] $γ(x)$ dadurch, dass an der Sprungstelle $x = 0$ der rechtsseitige Grenzwert „Eins” gültig ist $($anstelle des Mittelwertes „$0.5$” zwischen links– und rechtsseitigem Grenzwert$)$. |
| − | *Mit obiger VTF-Definition gilt dann für die Wahrscheinlichkeit von kontinuierlichen und diskreten Zufallsgrößen gleichermaßen, und natürlich auch für | + | *Mit obiger VTF-Definition gilt dann für die Wahrscheinlichkeit von kontinuierlichen und diskreten Zufallsgrößen gleichermaßen, und natürlich auch für gemischte Zufallsgrößen mit diskreten und kontinuierlichen Anteilen: |
:$${\rm Pr}(x_{\rm u}<x \le x_{\rm o})=F_x(x_{\rm o})-F_x(x_{\rm u}).$$ | :$${\rm Pr}(x_{\rm u}<x \le x_{\rm o})=F_x(x_{\rm o})-F_x(x_{\rm u}).$$ | ||
*Bei rein kontinuierlichen Zufallsgrößen könnten hier das „Kleiner”–Zeichen und das „Kleiner/Gleich”–Zeichen gegenseitig ersetzt werden. | *Bei rein kontinuierlichen Zufallsgrößen könnten hier das „Kleiner”–Zeichen und das „Kleiner/Gleich”–Zeichen gegenseitig ersetzt werden. | ||
:$${\rm Pr}(x_{\rm u}<x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x < x_{\rm o}) ={\rm Pr}(x_{\rm u}<x < x_{\rm o}).$$ | :$${\rm Pr}(x_{\rm u}<x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x < x_{\rm o}) ={\rm Pr}(x_{\rm u}<x < x_{\rm o}).$$ | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ | + | $\text{Beispiel 2:}$ Wird der Grauwert des [[Stochastische_Signaltheorie/Verteilungsfunktion#Verteilungsfunktion_bei_kontinuierlichen_Zufallsgr.C3.B6.C3.9Fen|ursprünglichen Lena–Fotos]] mit acht Stufen quantisiert, so dass jedes einzelne Pixel durch drei Bit dargestellt und digital übertragen werden kann, so ergibt sich die diskrete Zufallsgröße $q$. Durch die Quantisierung geht allerdings ein Teil der Bildinformation verloren, was sich im quantisierten Bild durch deutlich erkennbare „Konturen” auswirkt. |
| − | Wird | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Datei:P_ID74__Sto_T_3_2_S2b_neu.png |right|frame| WDF und VTF eines wertdiskreten Bildes]] | |
| − | Die rechts skizzierte Verteilungsfunktion $F_{q}(r)$ weist | + | *Die dazugehörige Wahrscheinlichkeitsdichtefunktion $f_{q}(q)$ setzt sich aus $M = 8$ Diracfunktionen zusammen, wobei bei der hier gewählten Quantisierung den möglichen Graustufen die Werte $q_\mu = (\mu – 1)/7$ mit $\mu = 1, 2,$ ... , $8$ zugeordnet sind. |
| + | *Die Gewichte der Diracfunktionen kann man aus der WDF $f_{x}(x)$ des Originalbildes berechnen. Man erhält | ||
| + | :$$p_\mu={\rm Pr}(q = q_\mu ) = {\rm Pr}(\frac{2\mu-\rm 3}{14}< {x} \le\frac{2\it \mu- \rm 1}{14}) $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} p_\mu={\rm Pr}(q = q_\mu ) = \int_{(2\it \mu- \rm 3)/14}^{(2\mu-1)/14}\it f_{x}{\rm (}x{\rm )}\,{\rm d}x.$$ | ||
| + | *Für die undefinierten Randbereiche $(x<0$ bzw. $x>1)$ ist hier jeweils $f_{x}(x) = 0$ zu setzen. | ||
| + | *Da im Originalbild die Graustufen $x ≈0$ („sehr tiefes Schwarz”) bzw. $x ≈1$ („nahezu reines Weiß”) weitgehend fehlen, ergeben sich die Wahrscheinlichkeiten $p_1 ≈ p_8 ≈ 0$. In der WDF–Grafik sind also nur sechs Diracfunktionen sichtbar. Die fehlenden Diracs bei $q = 0$ und $q =1$ sind nur durch Punkte angedeutet. | ||
| + | *Die rechts skizzierte Verteilungsfunktion $F_{q}(r)$ weist somit sechs Unstetigkeitsstellen auf, bei denen jeweils der rechtsseitige Grenzwert gültig ist.}} | ||
| − | Die in diesem Abschnitt behandelte Thematik ist im Lernvideo [[Zusammenhang_zwischen_WDF_und_VTF_(Lernvideo)|Zusammenhang zwischen WDF und VTF]] zusammengefasst. | + | Die in diesem Abschnitt behandelte Thematik ist im Lernvideo [[Zusammenhang_zwischen_WDF_und_VTF_(Lernvideo)|Zusammenhang zwischen WDF und VTF]] zusammengefasst. |
| Zeile 101: | Zeile 100: | ||
[[Aufgaben:3.2 cos²- und Dirac-VTF|Aufgabe 3.2: $\cos^2$– und Dirac–VTF]] | [[Aufgaben:3.2 cos²- und Dirac-VTF|Aufgabe 3.2: $\cos^2$– und Dirac–VTF]] | ||
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.2Z:_Zusammenhang_zwischen_WDF_und_VTF|Aufgabe 3.2Z: Zusammenhang zwischen WDF und VTF]] |
{{Display}} | {{Display}} | ||
Aktuelle Version vom 4. Januar 2022, 11:42 Uhr
Inhaltsverzeichnis
Zusammenhang zwischen WDF und VTF
Zur Beschreibung von Zufallsgrößen wird neben der Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ auch die Verteilungsfunktion $\rm (VTF)$ mit folgender Definition verwendet:
$\text{Definition:}$ Die Verteilungsfunktion $F_{x}(r)$ entspricht der Wahrscheinlichkeit, dass die Zufallsgröße $x$ kleiner oder gleich einem reellen Zahlenwert $r$ ist:
- $$F_{x}(r) = {\rm Pr}( x \le r).$$
Die englische Bezeichnung für die Verteilungsfunktion (VTF) ist "Cumulative Distribution Function" $\rm (CDF)$.
Bei einer kontinuierlichen Zufallsgröße sind bezüglich der Verteilungsfunktion folgende Aussagen möglich:
- Die Verteilungsfunktion ist aus der Wahrscheinlichkeitsdichtefunktion $f_{x}(x)$ durch Integration berechenbar. Es gilt:
- $$F_{x}(r) = \int_{-\infty}^{r}f_x(x)\,{\rm d}x.$$
- Da die WDF nie negativ ist, steigt $F_{x}(r)$ zumindest schwach monoton an, und liegt stets zwischen den folgenden Grenzwerten:
- $$F_{x}(r → \hspace{0.05cm} – \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{x}(r → +∞) = 1.$$
- Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch Differentiation bestimmen:
- $$f_{x}(x)=\frac{{\rm d} F_{x}(r)}{{\rm d} r}\Bigg |_{\hspace{0.1cm}r=x}.$$
- Der Zusatz „$r = x$” macht deutlich, dass bei unserer Nomenklatur das Argument der Wahrscheinlichkeitsdichtefunktion die Zufallsgröße selbst ist, während das VTF–Argument eine beliebige reelle Variable $r$ angibt.
$\text{Hinweise zur Nomenklatur:}$
Hätten wir bei den Definitionen von $\rm WDF$ und $\rm VTF$
- zwischen der Zufallsgröße $X$
- und den Realisierungen $x ∈ X$ unterschieden ⇒ $f_{X}(x), F_{X}(x)$,
so ergäbe sich folgende Nomenklatur:
- $$F_{X}(x) = {\rm Pr}(X \le x) = \int_{-\infty}^{x}f_{x}(\xi)\,{\rm d}\xi.$$
Leider haben wir uns zu Beginn unseres $\rm LNTwww$–Projektes (2001) aus durchaus berechtigten Gründen für unsere Nomenklatur entschieden, was nun (2017) nicht mehr zu ändern ist, auch im Hinblick auf die realisierten Lernvideos.
Wir bleiben also bei $f_{x}(x)$ anstelle von $f_{X}(x)$ sowie $F_{x}(r)$ anstelle von $F_{X}(x).$
Verteilungsfunktion bei kontinuierlichen Zufallsgrößen
Die im letzten Abschnitt angegebenen Gleichungen gelten nur für wertkontinuierliche Zufallsgrößen und sollen hier durch ein Beispiel verdeutlicht werden. Im nächsten Abschnitt wird gezeigt, dass für diskrete Zufallsgrößen die Gleichungen etwas modifiziert werden müssen.
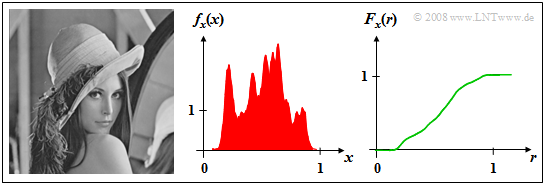
$\text{Beispiel 1:}$ Das linke Bild zeigt das Foto „Lena”, das häufig als Testvorlage für Bildcodierverfahren dient.
- Wird dieses Bild in $256 × 256$ Bildpunkte (Pixel) unterteilt, und ermittelt man für jedes einzelne Pixel die Helligkeit, so erhält man eine Folge $〈x_ν〉$ von Grauwerten. Deren Länge ist $N = 256^2 = 65536$.
- Der Grauwert $x$ ist eine wertkontinuierliche Zufallsgröße, wobei die Zuordnung zu Zahlenwerten willkürlich ist. Zum Beispiel sei „Schwarz” durch den Wert $x = 0$ und „Weiß” durch $x = 1$ charakterisiert. Der Zahlenwert $x =0.5$ kennzeichnet dann eine mittlere Graufärbung.
Im mittleren Bild ist die WDF $f_{x}(x)$ dargestellt, die in der Literatur auch oft als „Grauwertstatistik” bezeichnet wird.
- Es ist ersichtlich, dass im Originalbild einige Grauwerte bevorzugt sind und die beiden Extremwerte $x =0$ („tiefes Schwarz”) bzw. $x =1$ („reines Weiß”) nur sehr selten auftreten.
- Die Verteilungsfunktion $F_{x}(r)$ dieser kontinuierlichen Zufallsgröße ist stetig und steigt, wie das rechte Bild zeigt, von $0$ auf $1$ monoton an. Bei $r \approx 0$ und $r \approx 1$ verläuft die VTF aufgrund fehlender WDF–Anteile horizontal.
Anmerkung: Genau genommen ist bei einem am Computer darstellbaren Bild – im Gegensatz zu einem „analogen” Foto – der Grauwert stets eine wertdiskrete Zufallsgröße. Bei großer Auflösung der Farbinformation („Farbtiefe”) kann man diese Zufallsgröße allerdings näherungsweise als wertkontinuierlich betrachten.
Die in diesem Abschnitt behandelte Thematik ist im Lernvideo Zusammenhang zwischen WDF und VTF zusammengefasst.
Verteilungsfunktion bei diskreten Zufallsgrößen
Für die Berechnung der Verteilungsfunktion einer wertdiskreten Zufallsgröße $x$ aus deren WDF muss stets von einer allgemeineren Gleichung ausgegangen werden. Hier gilt mit mit der Hilfsvariablen $\varepsilon > 0$:
- $$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm}0}\int_{-\infty}^{r+\varepsilon}f_x(x)\,{\rm d}x.$$
- Die Berechnung der Verteilungsfunktion durch Grenzwertbildung ist aufgrund des „Kleiner/Gleich”–Zeichens in der allgemeinen Definition erforderlich.
- Berücksichtigt man zudem, dass bei einer diskreten Zufallsgröße die WDF aus einer Summe gewichteter Diracfunktionen besteht, so erhält man:
- $$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{r+\varepsilon}\sum\limits_{\mu= 1}^{ M}p_\mu\cdot \delta(x-x_\mu)\,{\rm d}x.$$
- Vertauscht man in der Gleichung Integration und Summation, und berücksichtigt, dass die Integration über die Diracfunktion die Sprungfunktion ergibt, so erhält man:
- $$F_{x}(r)=\sum\limits_{\mu= \rm 1}^{\it M}p_\mu\cdot \gamma_0 (r-x_\mu),\hspace{0.4cm}{\rm mit} \hspace{0.4cm}\gamma_0(x)=\lim_{\epsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{x+\varepsilon}\delta (u)\,{\rm d} u = \left\{ \begin{array}{*{2}{c}} 0 \hspace{0.4cm} {\rm falls}\hspace{0.1cm} x< 0,\\ 1 \hspace{0.4cm} {\rm falls}\hspace{0.1cm}x\ge 0. \\ \end{array} \right.$$
Hierzu ist anzumerken:
- Die Funktion $γ_0(x)$ unterscheidet sich von der in der Systemtheorie üblichen Sprungfunktion $γ(x)$ dadurch, dass an der Sprungstelle $x = 0$ der rechtsseitige Grenzwert „Eins” gültig ist $($anstelle des Mittelwertes „$0.5$” zwischen links– und rechtsseitigem Grenzwert$)$.
- Mit obiger VTF-Definition gilt dann für die Wahrscheinlichkeit von kontinuierlichen und diskreten Zufallsgrößen gleichermaßen, und natürlich auch für gemischte Zufallsgrößen mit diskreten und kontinuierlichen Anteilen:
- $${\rm Pr}(x_{\rm u}<x \le x_{\rm o})=F_x(x_{\rm o})-F_x(x_{\rm u}).$$
- Bei rein kontinuierlichen Zufallsgrößen könnten hier das „Kleiner”–Zeichen und das „Kleiner/Gleich”–Zeichen gegenseitig ersetzt werden.
- $${\rm Pr}(x_{\rm u}<x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x < x_{\rm o}) ={\rm Pr}(x_{\rm u}<x < x_{\rm o}).$$
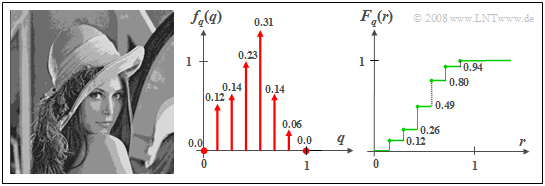
$\text{Beispiel 2:}$ Wird der Grauwert des ursprünglichen Lena–Fotos mit acht Stufen quantisiert, so dass jedes einzelne Pixel durch drei Bit dargestellt und digital übertragen werden kann, so ergibt sich die diskrete Zufallsgröße $q$. Durch die Quantisierung geht allerdings ein Teil der Bildinformation verloren, was sich im quantisierten Bild durch deutlich erkennbare „Konturen” auswirkt.
- Die dazugehörige Wahrscheinlichkeitsdichtefunktion $f_{q}(q)$ setzt sich aus $M = 8$ Diracfunktionen zusammen, wobei bei der hier gewählten Quantisierung den möglichen Graustufen die Werte $q_\mu = (\mu – 1)/7$ mit $\mu = 1, 2,$ ... , $8$ zugeordnet sind.
- Die Gewichte der Diracfunktionen kann man aus der WDF $f_{x}(x)$ des Originalbildes berechnen. Man erhält
- $$p_\mu={\rm Pr}(q = q_\mu ) = {\rm Pr}(\frac{2\mu-\rm 3}{14}< {x} \le\frac{2\it \mu- \rm 1}{14}) $$
- $$\Rightarrow \hspace{0.3cm} p_\mu={\rm Pr}(q = q_\mu ) = \int_{(2\it \mu- \rm 3)/14}^{(2\mu-1)/14}\it f_{x}{\rm (}x{\rm )}\,{\rm d}x.$$
- Für die undefinierten Randbereiche $(x<0$ bzw. $x>1)$ ist hier jeweils $f_{x}(x) = 0$ zu setzen.
- Da im Originalbild die Graustufen $x ≈0$ („sehr tiefes Schwarz”) bzw. $x ≈1$ („nahezu reines Weiß”) weitgehend fehlen, ergeben sich die Wahrscheinlichkeiten $p_1 ≈ p_8 ≈ 0$. In der WDF–Grafik sind also nur sechs Diracfunktionen sichtbar. Die fehlenden Diracs bei $q = 0$ und $q =1$ sind nur durch Punkte angedeutet.
- Die rechts skizzierte Verteilungsfunktion $F_{q}(r)$ weist somit sechs Unstetigkeitsstellen auf, bei denen jeweils der rechtsseitige Grenzwert gültig ist.
Die in diesem Abschnitt behandelte Thematik ist im Lernvideo Zusammenhang zwischen WDF und VTF zusammengefasst.
Aufgaben zum Kapitel
Aufgabe 3.2: $\cos^2$– und Dirac–VTF
Aufgabe 3.2Z: Zusammenhang zwischen WDF und VTF