Modulationsverfahren/Hüllkurvendemodulation: Unterschied zwischen den Versionen
| (27 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Funktionsweise bei idealen Bedingungen== | ==Funktionsweise bei idealen Bedingungen== | ||
| + | <br> | ||
Wir gehen zunächst von folgenden Voraussetzungen aus: | Wir gehen zunächst von folgenden Voraussetzungen aus: | ||
| − | *Das Quellensignal $q(t)$ sei gleichsignalfrei und betragsmäßig auf $q_{\rm max}$ begrenzt. | + | *Das Quellensignal $q(t)$ sei gleichsignalfrei und betragsmäßig auf $q_{\rm max}$ begrenzt. |
| − | *Die Übertragung basiert auf dem Modulationsverfahren „ZSB–AM mit Träger”. Zur einfacheren Darstellung wird die Trägerphase ohne Einschränkung der Allgemeingültigkeit $\mathbf{ϕ_{\rm T} } =$ | + | *Die Übertragung basiert auf dem Modulationsverfahren „ZSB–AM mit Träger”. |
| − | $$s(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$ | + | *Zur einfacheren Darstellung wird die Trägerphase ohne Einschränkung der Allgemeingültigkeit $\mathbf{ϕ_{\rm T} } = 0$ gesetzt: |
| − | *Der Modulationsgrad sei $m | + | :$$s(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$ |
| − | *Der Kanal sei ideal, das heißt, es gibt keine Verzerrungen, keine Dämpfung, keine Laufzeit und keine (Rausch–) Störungen. Mit $H_{\rm K}(f) =$ | + | *Der Modulationsgrad sei $m ≤ 1$. Aus der Definition $m = q_{\rm max}/A_{\rm T}$ folgt somit auch $q(t) + A_{\rm T} ≥ 0$. |
| − | $$r(t) = s(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$ | + | *Der Kanal sei ideal, das heißt, es gibt keine Verzerrungen, keine Dämpfung, keine Laufzeit und keine (Rausch–) Störungen. |
| − | *In dieser Gleichung bezeichnet $a(t)$ die Hüllkurve von $r(t)$. Die Phasenfunktion $\mathbf{ϕ}(t)$ | + | *Mit $H_{\rm K}(f) = 1$ und $n(t) \equiv 0$ erhält man somit für das Empfangssignal: |
| + | :$$r(t) = s(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$ | ||
| + | *In dieser Gleichung bezeichnet $a(t)$ die '''Hüllkurve''' von $r(t)$. Die Phasenfunktion sei $\mathbf{ϕ}(t) = 0$. | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ Ein '''Hüllkurvendemodulator''' detektiert die Hüllkurve $a(t)$ seines Eingangssignals $r(t)$ und gibt diese nach Eliminierung des Gleichanteils $A_{\rm T}$ als Sinkensignal aus: | ||
| + | :$$v(t) = a(t) - A_{\rm T}\hspace{0.05cm}.$$ | ||
| + | Die Entfernung des Gleichanteils $A_{\rm T}$ kann beispielsweise durch einen Hochpass realisiert werden, der alle Frequenzen bis auf $f = 0$ ungehindert passieren lässt.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | *Sind alle obigen Voraussetzungen erfüllt, so gilt $v(t) = q(t)$. | ||
| + | *Das bedeutet, dass mit einem (idealen) Hüllkurvendemodulator durchaus ein ideales Nachrichtenübertragungssystem realisiert werden kann. | ||
| − | |||
| + | [[Datei:P_ID1019__Mod_T_2_3_S1_neu.png|right|frame|Signalverläufe zur Verdeutlichung der Hüllkurvendemodulation]] | ||
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 1:}$ In der Grafik ist unten das Empfangssignal $r(t) = s(t)$ dargestellt, wobei „ZSB–AM mit Träger” zugrunde liegt $($Modulationsgrad $m = 0.5)$. | |
| + | *Die vom Hüllkurvendemodulator auszuwertende Hüllkurve $a(t)$ ist gleich der Summe aus dem Quellensignal $q(t)$ und dem beim Sender zugesetzten Gleichanteil $A_{\rm T}$. | ||
| + | *Für das Demodulatorausgangssignal nach Eliminierung des Gleichanteils $A_{\rm T}$ mit einem Hochpass gilt $v(t) = q(t)$, vorausgesetzt, dass das Quellensignal $q(t)$ keinen Gleichanteil beinhaltet hat. Ein solcher würde (fäschlicherweise) durch den Hochpass ebenfalls entfernt. }} | ||
| − | |||
| + | ==Realisierung eines Hüllkurvendemodulators== | ||
| + | [[Datei: P_ID1020__Mod_T_2_2_S2_v80Ganz_neu.png|frame|Prinzip der Hüllkurvendemodulation im Zeitbereich | rechts]] | ||
| + | Die nebenstehende Grafik zeigt | ||
| + | *oben eine einfache Realisierungsmöglichkeit des Hüllkurvendemodulators, | ||
| + | *unten die Signale $r(t)$ und $w(t)$ zur Verdeutlichung des Prinzips. | ||
| − | |||
| − | |||
| − | = | + | Betrachten Sie zunächst den mit $T = T_{\rm opt}$ bezeichneten mittleren Signalausschnitt. |
| − | |||
| − | |||
| − | + | Der erste Schaltungsteil – bestehend aus einer Diode und der Parallelschaltung eines Widerstandes $R$ und einer Kapazität $C$ – erfüllt folgende Aufgaben: | |
| + | *Ist das (hell)grau gezeichnete Signal $r(t)$ größer als die Spannung $w(t)$ an $R$ und $C$, so leitet die Diode, es gilt $w(t) = r(t)$ und die Kapazität $C$ wird aufgeladen. In diesen Bereichen ist das Signal $w(t)$ grün gezeichnet. | ||
| + | *Gilt $r(t) < w(t)$ wie zu den violett markierten Zeiten, so sperrt die Diode und die Kapazität entlädt sich über den Widerstand $R$. Das Signal $w(t)$ fällt exponentiell mit der Zeitkonstanten $T = R · C$ ab. | ||
| + | *Ab den mit Kreisen markierten Zeitpunkten gilt wieder $r(t) > w(t)$ und die Kapazität wird wieder aufgeladen. Man erkennt aus der Skizze, dass $w(t)$ „in etwa” mit der Hüllkurve $a(t)$ übereinstimmt. | ||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Design-Kriterien:}$ | ||
| + | *Die Abweichungen zwischen der Hüllkurven–Näherung $w(t)$ und dessen Sollfunktion $a(t)$ sind um so geringer, je größer die Trägerfrequenz $f_{\rm T}$ im Vergleich zur Bandbreite $B_{\rm NF}$ des niederfrequenten Nachrichtensignals ist. Als Richtwert wird oft $f_{\rm T} ≥ 100 · B_{\rm NF}$ angegeben. | ||
| + | *Gleichzeitig sollte die Zeitkonstante $T$ des RC–Parallelschwingkreises stets sehr viel größer als $1/f_{\rm T}$ und sehr viel kleiner als $1/B_{\rm NF}$ sein. | ||
| + | :$$1/f_{\rm T}\hspace{0.1cm} \ll \hspace{0.1cm} T \hspace{0.1cm} \ll \hspace{0.1cm} 1/B_{\rm NF} \hspace{0.05cm}, $$ | ||
| + | *Ein guter Kompromiss ist das geometrische Mittel zwischen beiden Grenzen: | ||
| + | :$$ T_{\rm opt} = {1}/{\sqrt{f_{\rm T} \cdot B_{\rm NF} } } \hspace{0.05cm}.$$ | ||
| + | *Ist die Zeitkonstante $T$ zu klein wie im linken Bereich obiger Skizze, so entlädt der Kondensator stets zu schnell und die Abweichung $w(t) \ – \ a(t)$ ist unnötig groß. | ||
| + | *Auch ein zu großer Wert $T > T_{\rm opt}$ führt zu einer Verschlechterung, wie im rechten Signalausschnitt dargestellt. In diesem Fall kann $w(t)$ der Hüllkurve $a(t)$ nicht mehr folgen.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ Bei einer NF–Bandbreite von $5 \ \rm kHz$ sollte die Trägerfrequenz mindestens $500 \ \rm kHz$ gewählt werden. | ||
| + | *Die Zeitkonstante $T$ muss sehr viel größer als $1/f_{\rm T} = 2 \ \rm µ s$ und gleichzeitig sehr viel kleiner als $1/B_{\rm NF} = 200 \ \rm µ s $ sein. | ||
| + | *Der optimale Wert entsprechend der Kompromissformel ist dann: | ||
| + | :$$T_{\rm opt} = 1/\sqrt{ 5 \cdot 10^5 \ {\rm Hz} \cdot 5 \cdot 10^3 \ {\rm Hz} } = 20 \ \rm µ s \hspace{0.05cm}.$$ }} | ||
| − | + | [[Datei:Mod_T_2_3_S2b_version2.png|right|frame|Frequenzbereichsdarstellung des Hüllkurvendemodulators]] | |
| − | + | Die rechte Grafik verdeutlicht die Wirkungsweise des Hüllkurvendemodulators im Frequenzbereich. Das Spektrum $W(f)$ des Signals $w(t)$ an der RC–Parallelschaltung unterscheidet sich vom Spektrum $Q(f)$ des Quellensignals wie folgt: | |
| − | $$ | + | *Aufgrund des beim Sender zugesetzten Trägersignals $z(t)$ beinhaltet die Spektralfunktion $W(f)$ eine Diraclinie bei $f = 0$ mit dem Gewicht $A_{\rm T}$ (Trägeramplitude). |
| − | + | * $W(f)$ weist zudem auch Spektralanteile im Bereich um die Trägerfrequenz $f_{\rm T}$ auf, die sich mit dem gezackten Zeitverlauf $w(t)$ erklären lassen (siehe erste Grafik zu diesem Abschnitt). | |
| + | *Auch im NF–Bereich unterscheidet sich $W(f)$ gegenüber $Q(f)$ geringfügig. Der Fehler wird dabei um so geringer sein, je größer die Trägerfrequenz im Vergleich zur NF-Bandbreite ist. | ||
| + | <br clear=all> | ||
| + | Die zwei erstgenannten Signalverfälschungen werden durch den Hochpass und den Tiefpass eliminiert, die zusammen einen Bandpass ergeben. Es bleibt aber auch eine geringfügige Abweichung zwischen dem Sinkensignal $v(t)$ und dem Quellensignal $q(t)$ im interessanten Bereich $0 < f < B_{\rm NF}$ erhalten, wie aus dem Vergleich des rot eingezeichneten Ausgangsspektrums $V(f)$ und des blau hinterlegten Eingangsspektrums $Q(f)$ hervorgeht. | ||
| − | == | + | ==Warum die Hüllkurvendemodulation bei $m > 1$ versagt== |
| − | Die | + | <br> |
| + | Die Grafik zeigt die ZSB–AM–Signale für $m = 0.5$ und $m = 2$. Aus dieser Darstellung erkennt man folgende Unterschiede: | ||
| + | [[Datei:Mod_T_2_3_S3_version2.png|right|frame|Hüllkurvendemodulation mit $m < 1$ (oben) und $m > 1$ (unten)]] | ||
| + | * Bei einem Modulationsgrad $m ≤ 1$ gilt für die Hüllkurve des Bandpass–Signals: | ||
| + | ::$$a(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$ | ||
| + | :Hier ist mit dem Hüllkurvendemodulator eine ideale Demodulation möglich ⇒ $v(t) = q(t)$, wenn man das unvermeidbare Rauschen außer Betracht lässt. | ||
| − | [[ | + | * Dagegen gilt bei $m > 1$ folgender Zusammenhang: |
| + | ::$$a(t) = | q(t) + A_{\rm T}|\hspace{0.05cm}.$$ | ||
| + | #Hier führt die Hüllkurvendemodulation stets zu [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|nichtlinearen Verzerrungen]]. | ||
| + | #Das Sinkensignal $v(t)$ wird nun auch neue Frequenzen beinhalten, die in $q(t)$ nicht vorhanden waren. | ||
| + | #Für den Gleichanteil (Erwartungswert) der Hüllkurve gilt in diesem Fall: <br> ${\rm E}[a(t)] \ne A_{\rm T}\hspace{0.05cm}.$ | ||
| + | #Da nun anstelle von $A_{\rm T}$ dieser Gleichanteil ${\rm E}[a(t)]$ durch den Hochpass entfernt wird, kommt es zusätzlich zu einer Pegelverschiebung. | ||
| + | ==Beschreibung mit Hilfe des äquivalenten Tiefpass–Signals== | ||
| + | <br> | ||
| + | Insbesondere dann, wenn das Quellensignal $q(t)$ als Summe mehrerer harmonischer Schwingungen dargestellt werden kann, ist eine Signalbeschreibung mit dem äquivalenten Tiefpass–Signal $r_{\rm TP}(t)$ äußerst vorteilhaft. Dieses wurde im Buch [[Signaldarstellung/Äquivalentes_Tiefpass-Signal_und_zugehörige_Spektralfunktion|Signaldarstellung]] ausführlich beschrieben. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Bitte beachten Sie:}$ Lässt man Rauschen/Störungen außer Betracht, so kann für das '''Empfangssignal''' geschrieben werden: | |
| − | + | :$$r(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t + \phi(t))\hspace{0.05cm}.$$}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Diese Gleichung gilt für jede Form der Amplitudenmodulation bei unterschiedlichen Randbedingungen: | Diese Gleichung gilt für jede Form der Amplitudenmodulation bei unterschiedlichen Randbedingungen: | ||
| Zeile 108: | Zeile 110: | ||
| − | Das dazugehörige äquivalente | + | {{BlaueBox|TEXT= |
| − | $$r_{\rm TP}(t) = a(t) \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.05cm} \phi(t)}\hspace{0.05cm}.$$ | + | $\text{Dann gilt:}$ Das dazugehörige '''äquivalente Tiefpass–Signal''' ist im allgemeinen Fall komplex und lautet: |
| + | :$$r_{\rm TP}(t) = a(t) \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi(t)}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Die in den Gleichungen enthaltenen Zeitfunktionen $a(t)$ und $ϕ(t)$ sind bei beiden Darstellungen identisch: | ||
| + | * $a(t)$ beschreibt die '''Hüllkurve''' (zeitabhängige Amplitude) des physikalischen Signals $r(t)$ bzw. den Betrag $\vert r_{\rm TP}(t) \vert $ des äquivalenten TP–Signals. Dieser wird bei Hüllkurvendemodulation detektiert. | ||
| + | * $ϕ(t)$ ist die '''zeitabhängige Phase'''. Diese Funktion beinhaltet alle Informationen über die Lage der Nulldurchgänge von $r(t)$ und gibt an, ob neben der Amplitudenmodulation eine zusätzliche Phasenmodulation wirksam ist.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
Im Fall der Zweiseitenband–Amplitudenmodulation gilt bei idealem Kanal: | Im Fall der Zweiseitenband–Amplitudenmodulation gilt bei idealem Kanal: | ||
| − | *Die Ortskurve – darunter versteht man die zeitabhängige Darstellung des Signals $r_{\rm TP}(t)$ in der komplexen Ebene – ist eine horizontale Gerade auf der reellen Achse. | + | *Die '''Ortskurve''' – darunter versteht man die zeitabhängige Darstellung des Signals $r_{\rm TP}(t)$ in der komplexen Ebene – ist eine horizontale Gerade auf der reellen Achse. |
| − | *Daraus folgt weiter, dass die Phasenfunktion nur die zwei Werte 0 und π ( | + | *Daraus folgt weiter, dass die Phasenfunktion nur die zwei Werte $0$ und $π$ $(180^\circ)$ annehmen kann. |
| − | * | + | :*Bei $m ≤ 1$ ist $ϕ(t) ≡ 0$ und die Hüllkurvendemodulation ist verzerrungsfrei anwendbar. |
| + | :*Bei $m > 1$ liegt ein Teil der Ortskurve in der linken Halbebene ⇒ es kommt es bei Anwendung der Hüllkurvendemodulation zu nichtlinearen Verzerrungen. | ||
| + | |||
| + | [[Datei: P_ID1023__Mod_T_2_3_S4_neu.png|right|frame|Ortskurven zur Beschreibung der Hüllkurvendemodulation]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 3:}$ Wir setzen voraus, dass das Quellensignal $q(t)$ alle Werte zwischen $±1\ \rm V$ annehmen kann. | ||
| + | *Durch Zusetzen eines Gleichanteils von $A_{\rm T} = 2\ \rm V$ ergibt sich eine ZSB–AM mit dem Modulationsgrad $m = 0.5$, deren Ortskurve in der linken Grafik zu sehen ist. | ||
| + | *$r_{\rm TP}(t)$ liegt immer in der rechten Halbebene. Die Zeigerlänge verändert sich entsprechend dem Nachrichtensignal $q(t)$. | ||
| − | + | Die rechte Grafik beschreibt die Ortskurve für $A_{\rm T} = 0.5 \ \rm V$ ⇒ $m = 2$. | |
| − | + | * $r_{\rm TP}(t)$ nimmt nun reelle Werte zwischen $-0.5\ \rm V$ und $1.5\ \rm V$ an. | |
| + | *Der Hüllkurvendemodulator kann nicht zwischen positiven und negativen Werten unterscheiden ⇒ es kommt zu nichtlinearen Verzerrungen. | ||
| − | [[ | + | Die entsprechenden physikalischen Signale $q(t)$, $r(t)$ sowie $v(t)$ zu diesem Beispiel finden Sie in der Grafik auf der [[Modulationsverfahren/Hüllkurvendemodulation#Warum_die_H.C3.BCllkurvendemodulation_bei_.7F.27.22.60UNIQ-MathJax103-QINU.60.22.27.7F_versagt|vorherigen Seite]].}} |
| + | ==Sonderfall eines cosinusförmigen Nachrichtensignals== | ||
| + | <br> | ||
| + | Zur quantitativen Erfassung der nichtlinearen Verzerrungen aufgrund eines Modulationsgrades $m> 1$ gehen wir von folgendem Szenario aus: | ||
| + | *cosinusförmiges Quellensignal: $q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t);$ | ||
| + | *ZSB–AM mit Träger: $s(t) = \left ( q(t) + A_{\rm T} \right ) \hspace{-0.05cm}\cdot \hspace{-0.05cm}\cos(\omega_{\rm N} \hspace{-0.05cm}\cdot \hspace{-0.05cm}t),$ $r(t) = s(t);$ | ||
| + | *Modulationsgrad: $m = A_{\rm N}/A_{\rm T} = 1.25;$ | ||
| + | *ideale Hüllkurvendemodulation: $a(t) = | q(t) + A_{\rm T}|; $ | ||
| + | *Eliminierung des Gleichanteils durch Tiefpass: $r(t) = a(t) - {\rm E}\big[a(t)\big].$ | ||
| − | |||
| − | Die | + | Die nachfolgende Grafik gilt für die Signalparameter $A_{\rm N} = 5 \ \rm V$, $f_{\rm N} = 2 \ \rm kHz$, $A_{\rm T} = 4 \ \rm V$ und $f_{\rm T} = 100\ \rm kHz$. Sie zeigt |
| − | {{ | + | * oben das Sinkensignal $v(t)$ im Vergleich zum Quellensignal $q(t)$, |
| + | * in der Mitte das Empfangssignal $r(t)$ sowie die Hüllkurve $a(t) = |r(t)|$, | ||
| + | *unten das Fehlersignal $ε(t) = v(t) \ – \ q(t)$ aufgrund von nichtlinearen Verzerrungen. | ||
| + | <br clear=all> | ||
| + | Anhand der Grafiken sind folgende Aussagen möglich: | ||
| + | [[Datei: P_ID2960__Mod_T_2_3_S5_neu.png |right|frame| Fehlersignal bei Hüllkurvendemodulation]] | ||
| + | |||
| + | *Ein Vergleich der Signale $q(t)$ und $a(t)$ zeigt, dass im Beispiel zu etwa $80\%$ aller Zeiten die Hüllkurve $a(t)$ das Quellensignal $q(t)$ in der Form richtig wiedergibt. | ||
| + | *Das Maximum von $a(t)$ ist allerdings um den zugesetzten Träger $A_{\rm T}$ deutlich größer als das Maximum von $q(t)$. | ||
| + | *Das Sinkensignal $v(t)$ unterscheidet sich von der Hüllkurve $a(t)$ durch den Erwartungswert ${\rm Ε}\big[a(t)\big]$, der vom Tiefpass des Hüllkurvendemodulators entfernt wird. | ||
| + | *Da ${\rm Ε}\big[a(t)\big] = 4.27 \ \rm V$ nicht mit $A_{\rm T} = 4 \ \rm V$ übereinstimmt, unterscheidet sich $v(t)$ von $q(t)$ auch in den Bereichen, in denen $a(t)$ richtig detektiert wird, und zwar um den konstanten Wert $0.27 \ \rm V$. | ||
| + | *Aus dem cosinusförmigen Quellensignal $q(t)$ wird ein Signal $v(t)$ mit Oberwellen: | ||
| + | :$$v(t) = A_{\rm 1} \cdot \cos(\omega_{\rm N} t ) +A_{\rm 2} \cdot \cos(2\omega_{\rm N} t | ||
| + | )+A_{\rm 3} \cdot \cos(3\omega_{\rm N} t )+ \text{...}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}A_{\rm 1} = 4.48\,{\rm V},\hspace{0.3cm}A_{\rm 2} = 0.46\,{\rm V},\hspace{0.3cm}A_{\rm 3} = -0.37\,{\rm V},\hspace{0.3cm} | ||
| + | A_{\rm 4} = 0.26\,{\rm V},\hspace{0.1cm}\text{...}$$ | ||
| + | *Damit erhält man für die einzelnen Klirrfaktoren sowie den Gesamtklirrfaktor entsprechend den Angaben im Buch [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen#Der_Klirrfaktor|Lineare zeitinvariante Systeme]]: | ||
| + | :$$K_2 ={|A_{\rm 2}|}/{A_{\rm 1}} = 0.102,\hspace{0.3cm}K_3 = | ||
| + | {|A_{\rm 3}|}/{A_{\rm 1}} = 0.082,\hspace{0.3cm}K_4 = | ||
| + | {|A_{\rm 4}|}/{A_{\rm 1}} = 0.058,\hspace{0.1cm}\text{...}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}K = \sqrt{K_2^2 + K_3^2 + K_4^2 +\text{...} } \approx 15 \%.$$ | ||
| − | = | + | Im Kapitel [[Modulationsverfahren/Qualitätskriterien#Untersuchungen_im_Hinblick_auf_Signalverzerrungen|Qualitätskriterien]] wurde gezeigt, dass damit auch das SNR $ρ_v = 1/K^2 ≈ 44$ festliegt. $ρ_v$ $($nicht aber $K)$ kann zudem auch dann als Qualitätskriterium herangezogen werden, wenn $q(t)$ mehr als eine Frequenz beinhaltet ⇒ Herleitung im Buch [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen#Der_Klirrfaktor|Lineare zeitinvariante Systeme]]. |
| − | |||
| − | + | ==Berücksichtigung von Kanalverzerrungen== | |
| − | + | <br> | |
| − | + | Für die folgenden Betrachtungen setzen wir das Modulationsverfahren „ZSB–AM mit Träger” sowie ein cosinusförmiges Quellensignal $q(t)$ voraus. Die Amplituden von Nachrichten– und Trägersignal seien $A_{\rm N} = 4 \ \rm V$ und $A_{\rm T} = 5 \ \rm V $ ⇒ Modulationsgrad $m = 0.8$. | |
| − | + | *Damit ist (ideale) Hüllkurvendemodulation prinzipiell anwendbar. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
| − | |||
| + | [[Datei: P_ID1028__Mod_T_2_3_S7_neu.png |right|frame|Spektren und Signale zur Verdeutlichung der Hüllkurvendemodulation]] | ||
| + | Die Grafik zeigt von oben nach unten | ||
| + | *die Spektren $S_{\rm TP}(f)$ und $R_{\rm TP}(f)$ des äquivalenten Tiefpass–Signals, die als reell angenommen werden, | ||
| + | *die äquivalenten Tiefpass–Signale $s_{\rm TP}(t)$ und $r_{\rm TP}(t)$ in der komplexen Ebene, und schließlich | ||
| + | *die physikalischen Signale $s(t)$ und $r(t)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Die linke Bildhälfte zeigt die Senderseite und gibt gleichzeitig die Verhältnisse am Empfänger bei idealem Kanal an. | |
| − | + | #Wegen des Modulationsgrades $m ≤ 1$ erkennt man in der Hüllkurve $a(t)$ das Quellensignal $q(t)$. | |
| + | #Demzufolge ist Hüllkurvendemodulation bei gewissen Voraussetzungen ohne Verzerrungen anwendbar, wie im $\text{Beispiel 4}$ gezeigt wird. | ||
| − | Die | + | |
| − | + | Die rechte Hälfte berücksichtigt unsymmetrische Verzerrungen durch den Kanal. | |
| − | + | #Der Träger wird hier mit $α_{\rm T} = 0.8$ gedämpft, das obere Seitenband sogar mit $α_{\rm O} = 0.5$. | |
| − | + | #Nun verläuft die Hüllkurve $a(t) ≠ q(t) + A_{\rm T}$ nicht mehr cosinusförmig. | |
| + | #Eine Hüllkurvendemodulation führt hier zu nichtlinearen Verzerrungen wie im $\text{Beispiel 5}$ gezeigt. | ||
| + | <br clear=all> | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 4:}$ Es gelte weiterhin $A_{\rm N} = 4 \ \rm V$ und $A_{\rm T} = 5 \rm V$ ⇒ Modulationsgrad $m = 0.8$. | ||
| + | Die Grafik verdeutlicht den Einsatz eines idealen Hüllkurvendemodulators bei idealem Kanal, wobei folgende Identitäten berücksichtigt sind: | ||
| + | [[Datei:Mod_T_2_3_S7a_version2.png|right|frame| Hüllkurvendemodulation bei idealem Kanal]] | ||
| + | :$$R_{\rm TP}(f) \hspace{-0.05cm}=\hspace{-0.05cm} S_{\rm TP}(f) \hspace{0.02cm}, \hspace{0.15cm} | ||
| + | r_{\rm TP}(t) \hspace{-0.05cm}=\hspace{-0.05cm} s_{\rm TP}(t) \hspace{0.02cm}, \hspace{0.15cm} | ||
| + | r(t) \hspace{-0.05cm}=\hspace{-0.05cm} s(t) \hspace{0.02cm}.$$ | ||
| − | + | Man erkennt aus diesen Darstellungen: | |
| + | #Der den Träger beschreibende rote Zeiger der Länge $A_{\rm T}$ liegt fest. | ||
| + | #Das obere Seitenband (blau) dreht in mathematisch positiver Richtung, das untere Seitenband (grün) entgegengesetzt. | ||
| + | #Da der blaue und der grüne Zeiger beide mit der gleichen Winkelgeschwindigkeit $ω_{\rm N}$ drehen, aber in entgegengesetzte Richtungen, ist die vektorielle Summe aller Zeiger stets reell. | ||
| + | #Ist der Modulationsgrad $m ≤ 1$, so gilt für alle Zeiten $r_{\rm TP}(t) ≥ 0$ und $ϕ(t) = 0$. Das bedeutet, dass die Nulldurchgänge des Empfangssignals $r(t)$ genau mit denen des Trägersignals $z(t)$ übereinstimmen. | ||
| + | #Die Hüllkurve $a(t)$ des Signals $r(t)$ ist gleich der resultierenden Zeigerlänge, also gleich dem Betrag von $r_{\rm TP}(t)$. Wegen $m< 1$ gilt $a(t) = q(t) + A_{\rm T}$. | ||
| + | #Bei den gegebenen Amplitudenwerten liegt die Ortskurve $r_{\rm TP}(t)$ auf der reellen Achse zwischen den Endpunkten $A_{\rm T} \ – \ A_{\rm N} = 1\ \rm V$ und $A_{\rm T} + A_{\rm N} = 9 \ \rm V$. | ||
| + | #Die Ortskurve auf der reellen Achse in rechter Halbebene ist ein Indiz dafür, dass das Nachrichtensignal durch Hüllkurvendemodulation verzerrungsfrei möglich ist.}} | ||
| − | |||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 5:}$ Betrachten wir nun die gleichen Grafiken für den verzerrenden Kanal mit | ||
| + | *$α_{\rm U} = 1$ ⇒ das untere Seitenband (USB) wird nicht verändert, | ||
| + | *$α_{\rm T} = 0.8$ ⇒ der Träger wird etwas gedämpft, | ||
| + | * $α_{\rm U} = 0.5$ ⇒ das obere Seitenband (OSB) wird mehr gedämpft. | ||
| + | [[Datei:Mod_T_2_3_S7b_version2.png|right|frame|Hüllkurvendemodulation bei verzerrendem Kanal]] | ||
| − | Die | + | <br>Die Grafiken lassen sich wie folgt interpretieren: |
| + | #Aufgrund der unterschiedlichen Längen von grünem Zeiger (USB) und blauem Zeiger (OSB) wird die Ortskurve zu einer Ellipse, deren Mittelpunkt durch den (roten) Träger festliegt. | ||
| + | #Der Winkel zwischen dem komplexwertigen $r_{\rm TP}(t)$ und dem Koordinatenursprung ist nun nicht mehr durchgängig $ϕ(t) = 0$, sondern schwankt zwischen $±ϕ_{\rm max}.$ | ||
| + | #Die maximale Phase ist gleich dem Winkel der Tangente an die Ellipse. Im physikalischen Signal führt $ϕ(t) ≠ 0$ zu Verschiebungen der Nulldurchgänge von $r(t)$ gegenüber seinen Solllagen – vorgegeben durch das Trägersignal $z(t)$. | ||
| + | #Der Betrag $a(t) = \vert r_{\rm TP}(t) \vert$ – also die Hüllkurve von $r(t)$ – ist nun nicht mehr cosinusförmig und das Signal nach dem Hüllkurvendemodulator beinhaltet außer der Frequenz $f_{\rm N}$ auch Oberwellen: <br> $v(t) = A_{\rm 1} \cdot \cos(\omega_{\rm N}\cdot t ) +A_{\rm 2} \cdot \cos(2\omega_{\rm N}\cdot t | ||
| + | )+A_{\rm 3} \cdot \cos(3\omega_{\rm N} \cdot t )+ \text{...}$ | ||
| + | #Diese führen zu nichtlinearen Verzerrungen und werden durch den Klirrfaktor $K$ erfasst. Mit $A_{\rm N} = 4 \ \rm V$, $A_{\rm T} = 5 \ \rm V$, $α_{\rm U} = 1$ und $α_{\rm T} = 0.8$ ergeben sich in Abhängigkeit von $α_{\rm O}$ folgende Zahlkenwerte: | ||
| − | + | ::: $α_{\rm O} = 1.00$: $K = 0$ ⇒ lediglich der Träger wird gedämpft, | |
| − | + | ::: $α_{\rm O} = 0.75$: $K ≈ 0.4\%$, | |
| − | $ | + | ::: $α_{\rm O} = 0.50$: $K ≈ 1.5\%$ ⇒ dieser Wert ist der Grafik zugrunde gelegt, |
| − | + | ::: $α_{\rm O} = 0.25$: $K ≈ 4\%$, | |
| − | + | ::: $α_{\rm O} = 0.00$: $K ≈ 10\%$ ⇒ vollständige Unterdrückung des OSB. | |
| − | |||
| + | Die Grafik gilt für $α_{\rm O} = 0.5$. Dann kommt es (allerdings ist beides mit dem bloßen Auge nur schwer zu erkennen) | ||
| + | :*zu Verschiebungen der Nulldurchgänge im Signal $r(t)$ um maximal $25^\circ\hspace{-0.05cm}/360^\circ ≈ 7\%$ der Trägerperiode $T_0$, und | ||
| + | :* zur Abweichung von der idealen Cosinusform ⇒ $K ≈ 1.5\%$ . }} | ||
| − | |||
| + | ==Symmetrische Kanalverzerrungen – Dämpfungsverzerrungen== | ||
| + | <br> | ||
| + | Ein wesentliches Ergebnis des letzten Abschnitts war, dass es bei unsymmetrischen linearen Verzerrungen auf dem Kanal zu nichtlinearen Verzerrungen bezüglich des Nachrichtensignals kommt. | ||
| + | *Wird dagegen das untere Seitenband in gleicher Weise gedämpft wie das obere Seitenband, so ist die Ortskurve wieder eine horizontale Gerade und es entstehen keine nichtlinearen Verzerrungen. | ||
| + | *Vielmehr sind dann die Verzerrungen bezüglich $q(t)$ und $v(t)$ – ebenso wie die Verzerrungen bezüglich $s(t)$ und $r(t)$ – linear und können durch ein geeignet dimensioniertes Filter entzerrt werden. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Wir gehen hier von folgenden Voraussetzungen aus: | |
| − | + | *Quellensignal $q(t)$ – bestehend aus zwei Cosinusanteilen bei den Frequenzen $f_1$ und $f_2$ mit den Amplituden $A_1$ und $A_2$; | |
| + | *ZSB–AM mit Träger ⇒ das Sendesignal $s(t)$ setzt sich aus insgesamt fünf Cosinusschwingungen bei den Frequenzen $f_{\rm T}, f_{\rm T} ± f_1$ und $f_{\rm T} ± f_2$ zusammen; | ||
| + | [[Datei:Mod_T_2_3_S6_version2.png|right|frame|Spektren im äquivalenten Tiefpass-Bereich]] | ||
| + | *Kanal mit Dämpfungsverzerrungen, symmetrisch um die Trägerfrequenz: | ||
| + | :$$H_{\rm K} (f = f_{\rm T})= \alpha_0, \hspace{0.3cm} H_{\rm K} (f | ||
| + | = \pm f_{\rm 1})= \alpha_1, \hspace{0.3cm}H_{\rm K} (f = \pm | ||
| + | f_{\rm 2})= \alpha_2;$$ | ||
| + | *Idealer Hüllkurvendemodulator gemäß der Beschreibung in diesem Abschnitt. | ||
| − | + | Die Grafik zeigt die Spektralfunktionen der äquivalenten Tiefpass–Signale von Sende– und Empfangssignal. Anhand dieses Bildes sind folgende Aussagen möglich: | |
| + | #Das äquivalente Tiefpass–Signal $r_{\rm TP}(t)$ ist reell. Die Ortskurve – also die Spitze des Zeigerverbundes in der komplexen Ebene – liegt auch hier wieder auf der reellen Achse. | ||
| + | #Ist $α_0 · A_{\rm T}$ größer als $α_1 · A_1 + α_2 · A_2$, so ist der „Modulationsgrad des Empfangssignals” kleiner als $1$ und es kommt nicht zu nichtlinearen Verzerrungen. | ||
| + | #Das Sinkensignal nach idealer Hüllkurvendemodulation und Eliminierung des Gleichanteils $α_0 · A_{\rm T}$ durch den folgenden Hochpass lautet: | ||
| + | ::$$v(t) = \alpha_1 \cdot A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) + | ||
| + | \alpha_2 \cdot A_{\rm 2} \cdot \cos(2 \pi f_{\rm 2} t ) \hspace{0.05cm}.$$ | ||
| + | Das bedeutet: | ||
| + | *'''Es kommt zu linearen Verzerrungen (Dämpfungsverzerrungen), falls $α_2 ≠ α_1$ ist'''. | ||
| + | *'''Wäre die Symmetrie bezüglich $f_{\rm T}$ nicht gegeben, so würden nichtlineare Verzerrungen entstehen'''. | ||
| − | + | Wir verweisen hier auf das Lernvideo [[Lineare_und_nichtlineare_Verzerrungen_(Lernvideo)|Lineare und nichtlineare Verzerrungen]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Einfluss von additivem weißen Gaußschen Rauschen== | ||
| + | <br> | ||
| + | Ausgehend von der Systemkonfiguration | ||
| + | *ZSB–Amplitudenmodulation mit Modulationsgrad $m ≤ 1$ sowie | ||
| + | *bestmöglich angepasste Hüllkurvendemodulation | ||
| − | |||
| − | |||
| − | |||
| + | wird nun der Einfluss von additivem Rauschen abgeschätzt. Verzerrungen jeglicher Art – beispielsweise bedingt durch einen ungeeigneten Kanal oder die nichtperfekte Realisierung von Modulator und Demodulator – werden ausgeschlossen. | ||
| − | + | Die Grafik zeigt den Sinkenstörabstand $10 · \lg \, ρ_v$ bei unterschiedlichem Modulationsgrad $m$ in Abhängigkeit der logarithmierten Leistungskenngröße | |
| + | [[Datei: P_ID1031__Mod_T_2_3_S8_neu.png |right|frame| Sinkenstörabstand bei „ZSB-AM mit/ohne Träger” und Hüllkurvendemodulation]] | ||
| + | :$$10 \cdot {\rm lg }\hspace{0.1cm} \xi = 10 \cdot {\rm lg }\hspace{0.1cm} \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \hspace{0.05cm}.$$ | ||
| − | + | Das Ergebnis des Hüllkurvendemodulators ist mit durchgezogenen Linien markiert, während die gestrichelten Geraden den Synchrondemodulator kennzeichnen. | |
| − | |||
| − | + | Wie bereits in Kapitel [[Modulationsverfahren/Qualitätskriterien#Untersuchungen_im_Hinblick_auf_Signalverzerrungen|Untersuchungen im Hinblick auf Signalverzerrungen]] hergeleitet wurde, ergeben sich für den Synchrondemodulator $\rm (SD)$ in dieser doppelt–logarithmischen Darstellung | |
| − | + | *die Winkelhalbierende (für $m → ∞$, ZSB–AM ohne Träger), bzw. | |
| − | + | *hierzu parallel verschobene Gerade mit vertikalem Abstand $10 · \lg \, (1 + 2/m^2$). | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Bei Anwendung von Hüllkurvendemodulation $\rm (HKD)$ sind folgende Unterschiede festzustellen: | ||
| + | *Ein Hüllkurvendemodulator ist für $m > 1$ nicht sinnvoll. Dadurch würden starke nichtlineare Verzerrungen entstehen. | ||
| + | *Die durchgehend gezeichneten $\rm HKD$–Kurven liegen stets unterhalb der gestrichelten $\rm SD$–Geraden, wenn man vom gleichen Modulationsgrad $m$ ausgeht. | ||
| + | *Ab einem gewissen Wert der Leistungskenngröße $ξ$ sind allerdings die $\rm HKD$–Kurven von den $\rm SD$–Geraden innerhalb der Zeichengenauigkeit nicht mehr zu unterscheiden. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Mehr Informationen zu dieser Thematik finden Sie beispielsweise in [Kam 04]<ref>Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.</ref>. | ||
| − | |||
| − | + | ==Argumente für und gegen den Hüllkurvendemodulator== | |
| + | <br> | ||
| + | Der wichtigste Grund für die Verwendung des Hüllkurvendemodulators ist (besser gesagt: war), dass damit die oft aufwändige Frequenz– und Phasensynchronisation vermieden wurde, so dass dieser preisgünstig realisiert werden konnte. Der Hüllkurvendemodulator ist somit ein Beispiel eines "inkohärenten Demodulators". | ||
| + | Für den [[Modulationsverfahren/Synchrondemodulation|Synchrondemodulator]] und gegen den Hüllkurvendemodulator können dagegen mehrere Gründe angeführt werden: | ||
| + | *Bei Hüllkurvendemodulation muss eine Übermodulation $(m > 1)$ unter allen Umständen vermieden werden. Dies erreicht man beispielsweise durch die Amplitudenbegrenzung des Quellensignals, was aber ebenfalls nichtlineare Verzerrungen zur Folge hat. | ||
| + | *Bei sonst gleichen Randbedingungen ist ein Modulationsgrad $m < 1$ nur durch die Erhöhung der Sendeleistung um mindestens den Faktor $3$ zu erreichen. Dies ist auch wegen der berechtigten Diskussionen zum Thema „Elektro-Smog” in großen Teilen unserer Gesellschaft problematisch. | ||
| + | *Lineare Kanalverzerrungen können bei einem Hüllkurvendemodulator zu irreversiblen nichtlinearen Verzerrungen führen, während die bei Synchrondemodulation entstehenden linearen Verzerrungen möglicherweise durch besondere Maßnahmen beim Empfänger kompensiert werden können. | ||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:Aufgabe_2.7:_Ist_der_Modulationsgrad_zu_groß%3F|Aufgabe 2.7: Ist der Modulationsgrad zu groß?]] | ||
| + | [[Aufgaben:Aufgabe_2.7Z:_ZSB-AM_und_Hüllkurvendemodulator|Aufgabe 2.7Z: ZSB-AM und Hüllkurvendemodulator]] | ||
| + | [[Aufgaben:Aufgabe_2.8:_Unsymmetrischer_Kanal|Aufgabe 2.8: Unsymmetrischer Kanal]] | ||
| + | [[Aufgaben:Aufgabe_2.9:_Symmetrische_Verzerrungen|Aufgabe 2.9: Symmetrische Verzerrungen]] | ||
| + | ==Quellenverzeichnis== | ||
| + | <references/> | ||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 9. Januar 2022, 15:54 Uhr
Inhaltsverzeichnis
- 1 Funktionsweise bei idealen Bedingungen
- 2 Realisierung eines Hüllkurvendemodulators
- 3 Warum die Hüllkurvendemodulation bei $m > 1$ versagt
- 4 Beschreibung mit Hilfe des äquivalenten Tiefpass–Signals
- 5 Sonderfall eines cosinusförmigen Nachrichtensignals
- 6 Berücksichtigung von Kanalverzerrungen
- 7 Symmetrische Kanalverzerrungen – Dämpfungsverzerrungen
- 8 Einfluss von additivem weißen Gaußschen Rauschen
- 9 Argumente für und gegen den Hüllkurvendemodulator
- 10 Aufgaben zum Kapitel
- 11 Quellenverzeichnis
Funktionsweise bei idealen Bedingungen
Wir gehen zunächst von folgenden Voraussetzungen aus:
- Das Quellensignal $q(t)$ sei gleichsignalfrei und betragsmäßig auf $q_{\rm max}$ begrenzt.
- Die Übertragung basiert auf dem Modulationsverfahren „ZSB–AM mit Träger”.
- Zur einfacheren Darstellung wird die Trägerphase ohne Einschränkung der Allgemeingültigkeit $\mathbf{ϕ_{\rm T} } = 0$ gesetzt:
- $$s(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$
- Der Modulationsgrad sei $m ≤ 1$. Aus der Definition $m = q_{\rm max}/A_{\rm T}$ folgt somit auch $q(t) + A_{\rm T} ≥ 0$.
- Der Kanal sei ideal, das heißt, es gibt keine Verzerrungen, keine Dämpfung, keine Laufzeit und keine (Rausch–) Störungen.
- Mit $H_{\rm K}(f) = 1$ und $n(t) \equiv 0$ erhält man somit für das Empfangssignal:
- $$r(t) = s(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$
- In dieser Gleichung bezeichnet $a(t)$ die Hüllkurve von $r(t)$. Die Phasenfunktion sei $\mathbf{ϕ}(t) = 0$.
$\text{Definition:}$ Ein Hüllkurvendemodulator detektiert die Hüllkurve $a(t)$ seines Eingangssignals $r(t)$ und gibt diese nach Eliminierung des Gleichanteils $A_{\rm T}$ als Sinkensignal aus:
- $$v(t) = a(t) - A_{\rm T}\hspace{0.05cm}.$$
Die Entfernung des Gleichanteils $A_{\rm T}$ kann beispielsweise durch einen Hochpass realisiert werden, der alle Frequenzen bis auf $f = 0$ ungehindert passieren lässt.
- Sind alle obigen Voraussetzungen erfüllt, so gilt $v(t) = q(t)$.
- Das bedeutet, dass mit einem (idealen) Hüllkurvendemodulator durchaus ein ideales Nachrichtenübertragungssystem realisiert werden kann.
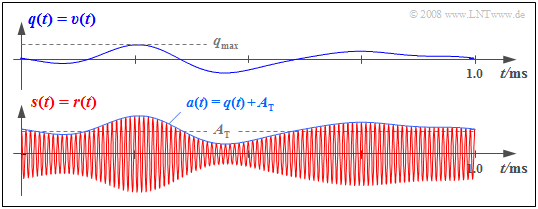
$\text{Beispiel 1:}$ In der Grafik ist unten das Empfangssignal $r(t) = s(t)$ dargestellt, wobei „ZSB–AM mit Träger” zugrunde liegt $($Modulationsgrad $m = 0.5)$.
- Die vom Hüllkurvendemodulator auszuwertende Hüllkurve $a(t)$ ist gleich der Summe aus dem Quellensignal $q(t)$ und dem beim Sender zugesetzten Gleichanteil $A_{\rm T}$.
- Für das Demodulatorausgangssignal nach Eliminierung des Gleichanteils $A_{\rm T}$ mit einem Hochpass gilt $v(t) = q(t)$, vorausgesetzt, dass das Quellensignal $q(t)$ keinen Gleichanteil beinhaltet hat. Ein solcher würde (fäschlicherweise) durch den Hochpass ebenfalls entfernt.
Realisierung eines Hüllkurvendemodulators
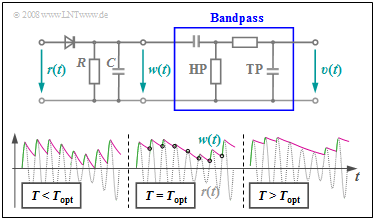
Die nebenstehende Grafik zeigt
- oben eine einfache Realisierungsmöglichkeit des Hüllkurvendemodulators,
- unten die Signale $r(t)$ und $w(t)$ zur Verdeutlichung des Prinzips.
Betrachten Sie zunächst den mit $T = T_{\rm opt}$ bezeichneten mittleren Signalausschnitt.
Der erste Schaltungsteil – bestehend aus einer Diode und der Parallelschaltung eines Widerstandes $R$ und einer Kapazität $C$ – erfüllt folgende Aufgaben:
- Ist das (hell)grau gezeichnete Signal $r(t)$ größer als die Spannung $w(t)$ an $R$ und $C$, so leitet die Diode, es gilt $w(t) = r(t)$ und die Kapazität $C$ wird aufgeladen. In diesen Bereichen ist das Signal $w(t)$ grün gezeichnet.
- Gilt $r(t) < w(t)$ wie zu den violett markierten Zeiten, so sperrt die Diode und die Kapazität entlädt sich über den Widerstand $R$. Das Signal $w(t)$ fällt exponentiell mit der Zeitkonstanten $T = R · C$ ab.
- Ab den mit Kreisen markierten Zeitpunkten gilt wieder $r(t) > w(t)$ und die Kapazität wird wieder aufgeladen. Man erkennt aus der Skizze, dass $w(t)$ „in etwa” mit der Hüllkurve $a(t)$ übereinstimmt.
$\text{Design-Kriterien:}$
- Die Abweichungen zwischen der Hüllkurven–Näherung $w(t)$ und dessen Sollfunktion $a(t)$ sind um so geringer, je größer die Trägerfrequenz $f_{\rm T}$ im Vergleich zur Bandbreite $B_{\rm NF}$ des niederfrequenten Nachrichtensignals ist. Als Richtwert wird oft $f_{\rm T} ≥ 100 · B_{\rm NF}$ angegeben.
- Gleichzeitig sollte die Zeitkonstante $T$ des RC–Parallelschwingkreises stets sehr viel größer als $1/f_{\rm T}$ und sehr viel kleiner als $1/B_{\rm NF}$ sein.
- $$1/f_{\rm T}\hspace{0.1cm} \ll \hspace{0.1cm} T \hspace{0.1cm} \ll \hspace{0.1cm} 1/B_{\rm NF} \hspace{0.05cm}, $$
- Ein guter Kompromiss ist das geometrische Mittel zwischen beiden Grenzen:
- $$ T_{\rm opt} = {1}/{\sqrt{f_{\rm T} \cdot B_{\rm NF} } } \hspace{0.05cm}.$$
- Ist die Zeitkonstante $T$ zu klein wie im linken Bereich obiger Skizze, so entlädt der Kondensator stets zu schnell und die Abweichung $w(t) \ – \ a(t)$ ist unnötig groß.
- Auch ein zu großer Wert $T > T_{\rm opt}$ führt zu einer Verschlechterung, wie im rechten Signalausschnitt dargestellt. In diesem Fall kann $w(t)$ der Hüllkurve $a(t)$ nicht mehr folgen.
$\text{Beispiel 2:}$ Bei einer NF–Bandbreite von $5 \ \rm kHz$ sollte die Trägerfrequenz mindestens $500 \ \rm kHz$ gewählt werden.
- Die Zeitkonstante $T$ muss sehr viel größer als $1/f_{\rm T} = 2 \ \rm µ s$ und gleichzeitig sehr viel kleiner als $1/B_{\rm NF} = 200 \ \rm µ s $ sein.
- Der optimale Wert entsprechend der Kompromissformel ist dann:
- $$T_{\rm opt} = 1/\sqrt{ 5 \cdot 10^5 \ {\rm Hz} \cdot 5 \cdot 10^3 \ {\rm Hz} } = 20 \ \rm µ s \hspace{0.05cm}.$$
Die rechte Grafik verdeutlicht die Wirkungsweise des Hüllkurvendemodulators im Frequenzbereich. Das Spektrum $W(f)$ des Signals $w(t)$ an der RC–Parallelschaltung unterscheidet sich vom Spektrum $Q(f)$ des Quellensignals wie folgt:
- Aufgrund des beim Sender zugesetzten Trägersignals $z(t)$ beinhaltet die Spektralfunktion $W(f)$ eine Diraclinie bei $f = 0$ mit dem Gewicht $A_{\rm T}$ (Trägeramplitude).
- $W(f)$ weist zudem auch Spektralanteile im Bereich um die Trägerfrequenz $f_{\rm T}$ auf, die sich mit dem gezackten Zeitverlauf $w(t)$ erklären lassen (siehe erste Grafik zu diesem Abschnitt).
- Auch im NF–Bereich unterscheidet sich $W(f)$ gegenüber $Q(f)$ geringfügig. Der Fehler wird dabei um so geringer sein, je größer die Trägerfrequenz im Vergleich zur NF-Bandbreite ist.
Die zwei erstgenannten Signalverfälschungen werden durch den Hochpass und den Tiefpass eliminiert, die zusammen einen Bandpass ergeben. Es bleibt aber auch eine geringfügige Abweichung zwischen dem Sinkensignal $v(t)$ und dem Quellensignal $q(t)$ im interessanten Bereich $0 < f < B_{\rm NF}$ erhalten, wie aus dem Vergleich des rot eingezeichneten Ausgangsspektrums $V(f)$ und des blau hinterlegten Eingangsspektrums $Q(f)$ hervorgeht.
Warum die Hüllkurvendemodulation bei $m > 1$ versagt
Die Grafik zeigt die ZSB–AM–Signale für $m = 0.5$ und $m = 2$. Aus dieser Darstellung erkennt man folgende Unterschiede:
- Bei einem Modulationsgrad $m ≤ 1$ gilt für die Hüllkurve des Bandpass–Signals:
- $$a(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$
- Hier ist mit dem Hüllkurvendemodulator eine ideale Demodulation möglich ⇒ $v(t) = q(t)$, wenn man das unvermeidbare Rauschen außer Betracht lässt.
- Dagegen gilt bei $m > 1$ folgender Zusammenhang:
- $$a(t) = | q(t) + A_{\rm T}|\hspace{0.05cm}.$$
- Hier führt die Hüllkurvendemodulation stets zu nichtlinearen Verzerrungen.
- Das Sinkensignal $v(t)$ wird nun auch neue Frequenzen beinhalten, die in $q(t)$ nicht vorhanden waren.
- Für den Gleichanteil (Erwartungswert) der Hüllkurve gilt in diesem Fall:
${\rm E}[a(t)] \ne A_{\rm T}\hspace{0.05cm}.$ - Da nun anstelle von $A_{\rm T}$ dieser Gleichanteil ${\rm E}[a(t)]$ durch den Hochpass entfernt wird, kommt es zusätzlich zu einer Pegelverschiebung.
Beschreibung mit Hilfe des äquivalenten Tiefpass–Signals
Insbesondere dann, wenn das Quellensignal $q(t)$ als Summe mehrerer harmonischer Schwingungen dargestellt werden kann, ist eine Signalbeschreibung mit dem äquivalenten Tiefpass–Signal $r_{\rm TP}(t)$ äußerst vorteilhaft. Dieses wurde im Buch Signaldarstellung ausführlich beschrieben.
$\text{Bitte beachten Sie:}$ Lässt man Rauschen/Störungen außer Betracht, so kann für das Empfangssignal geschrieben werden:
- $$r(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t + \phi(t))\hspace{0.05cm}.$$
Diese Gleichung gilt für jede Form der Amplitudenmodulation bei unterschiedlichen Randbedingungen:
- Zweiseitenband (ZSB) oder Einseitenband (ESB),
- mit oder ohne Träger,
- idealer Kanal oder linear verzerrender Kanal.
$\text{Dann gilt:}$ Das dazugehörige äquivalente Tiefpass–Signal ist im allgemeinen Fall komplex und lautet:
- $$r_{\rm TP}(t) = a(t) \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi(t)}\hspace{0.05cm}.$$
Die in den Gleichungen enthaltenen Zeitfunktionen $a(t)$ und $ϕ(t)$ sind bei beiden Darstellungen identisch:
- $a(t)$ beschreibt die Hüllkurve (zeitabhängige Amplitude) des physikalischen Signals $r(t)$ bzw. den Betrag $\vert r_{\rm TP}(t) \vert $ des äquivalenten TP–Signals. Dieser wird bei Hüllkurvendemodulation detektiert.
- $ϕ(t)$ ist die zeitabhängige Phase. Diese Funktion beinhaltet alle Informationen über die Lage der Nulldurchgänge von $r(t)$ und gibt an, ob neben der Amplitudenmodulation eine zusätzliche Phasenmodulation wirksam ist.
Im Fall der Zweiseitenband–Amplitudenmodulation gilt bei idealem Kanal:
- Die Ortskurve – darunter versteht man die zeitabhängige Darstellung des Signals $r_{\rm TP}(t)$ in der komplexen Ebene – ist eine horizontale Gerade auf der reellen Achse.
- Daraus folgt weiter, dass die Phasenfunktion nur die zwei Werte $0$ und $π$ $(180^\circ)$ annehmen kann.
- Bei $m ≤ 1$ ist $ϕ(t) ≡ 0$ und die Hüllkurvendemodulation ist verzerrungsfrei anwendbar.
- Bei $m > 1$ liegt ein Teil der Ortskurve in der linken Halbebene ⇒ es kommt es bei Anwendung der Hüllkurvendemodulation zu nichtlinearen Verzerrungen.
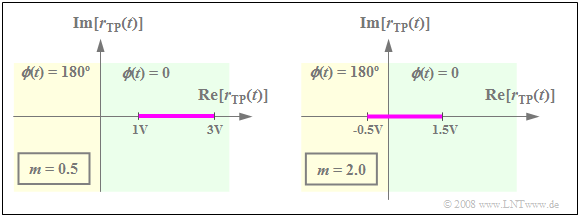
$\text{Beispiel 3:}$ Wir setzen voraus, dass das Quellensignal $q(t)$ alle Werte zwischen $±1\ \rm V$ annehmen kann.
- Durch Zusetzen eines Gleichanteils von $A_{\rm T} = 2\ \rm V$ ergibt sich eine ZSB–AM mit dem Modulationsgrad $m = 0.5$, deren Ortskurve in der linken Grafik zu sehen ist.
- $r_{\rm TP}(t)$ liegt immer in der rechten Halbebene. Die Zeigerlänge verändert sich entsprechend dem Nachrichtensignal $q(t)$.
Die rechte Grafik beschreibt die Ortskurve für $A_{\rm T} = 0.5 \ \rm V$ ⇒ $m = 2$.
- $r_{\rm TP}(t)$ nimmt nun reelle Werte zwischen $-0.5\ \rm V$ und $1.5\ \rm V$ an.
- Der Hüllkurvendemodulator kann nicht zwischen positiven und negativen Werten unterscheiden ⇒ es kommt zu nichtlinearen Verzerrungen.
Die entsprechenden physikalischen Signale $q(t)$, $r(t)$ sowie $v(t)$ zu diesem Beispiel finden Sie in der Grafik auf der vorherigen Seite.
Sonderfall eines cosinusförmigen Nachrichtensignals
Zur quantitativen Erfassung der nichtlinearen Verzerrungen aufgrund eines Modulationsgrades $m> 1$ gehen wir von folgendem Szenario aus:
- cosinusförmiges Quellensignal: $q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t);$
- ZSB–AM mit Träger: $s(t) = \left ( q(t) + A_{\rm T} \right ) \hspace{-0.05cm}\cdot \hspace{-0.05cm}\cos(\omega_{\rm N} \hspace{-0.05cm}\cdot \hspace{-0.05cm}t),$ $r(t) = s(t);$
- Modulationsgrad: $m = A_{\rm N}/A_{\rm T} = 1.25;$
- ideale Hüllkurvendemodulation: $a(t) = | q(t) + A_{\rm T}|; $
- Eliminierung des Gleichanteils durch Tiefpass: $r(t) = a(t) - {\rm E}\big[a(t)\big].$
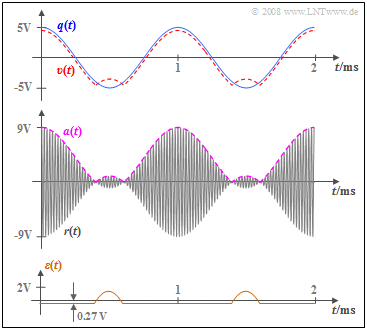
Die nachfolgende Grafik gilt für die Signalparameter $A_{\rm N} = 5 \ \rm V$, $f_{\rm N} = 2 \ \rm kHz$, $A_{\rm T} = 4 \ \rm V$ und $f_{\rm T} = 100\ \rm kHz$. Sie zeigt
- oben das Sinkensignal $v(t)$ im Vergleich zum Quellensignal $q(t)$,
- in der Mitte das Empfangssignal $r(t)$ sowie die Hüllkurve $a(t) = |r(t)|$,
- unten das Fehlersignal $ε(t) = v(t) \ – \ q(t)$ aufgrund von nichtlinearen Verzerrungen.
Anhand der Grafiken sind folgende Aussagen möglich:
- Ein Vergleich der Signale $q(t)$ und $a(t)$ zeigt, dass im Beispiel zu etwa $80\%$ aller Zeiten die Hüllkurve $a(t)$ das Quellensignal $q(t)$ in der Form richtig wiedergibt.
- Das Maximum von $a(t)$ ist allerdings um den zugesetzten Träger $A_{\rm T}$ deutlich größer als das Maximum von $q(t)$.
- Das Sinkensignal $v(t)$ unterscheidet sich von der Hüllkurve $a(t)$ durch den Erwartungswert ${\rm Ε}\big[a(t)\big]$, der vom Tiefpass des Hüllkurvendemodulators entfernt wird.
- Da ${\rm Ε}\big[a(t)\big] = 4.27 \ \rm V$ nicht mit $A_{\rm T} = 4 \ \rm V$ übereinstimmt, unterscheidet sich $v(t)$ von $q(t)$ auch in den Bereichen, in denen $a(t)$ richtig detektiert wird, und zwar um den konstanten Wert $0.27 \ \rm V$.
- Aus dem cosinusförmigen Quellensignal $q(t)$ wird ein Signal $v(t)$ mit Oberwellen:
- $$v(t) = A_{\rm 1} \cdot \cos(\omega_{\rm N} t ) +A_{\rm 2} \cdot \cos(2\omega_{\rm N} t )+A_{\rm 3} \cdot \cos(3\omega_{\rm N} t )+ \text{...}$$
- $$\Rightarrow \hspace{0.3cm}A_{\rm 1} = 4.48\,{\rm V},\hspace{0.3cm}A_{\rm 2} = 0.46\,{\rm V},\hspace{0.3cm}A_{\rm 3} = -0.37\,{\rm V},\hspace{0.3cm} A_{\rm 4} = 0.26\,{\rm V},\hspace{0.1cm}\text{...}$$
- Damit erhält man für die einzelnen Klirrfaktoren sowie den Gesamtklirrfaktor entsprechend den Angaben im Buch Lineare zeitinvariante Systeme:
- $$K_2 ={|A_{\rm 2}|}/{A_{\rm 1}} = 0.102,\hspace{0.3cm}K_3 = {|A_{\rm 3}|}/{A_{\rm 1}} = 0.082,\hspace{0.3cm}K_4 = {|A_{\rm 4}|}/{A_{\rm 1}} = 0.058,\hspace{0.1cm}\text{...}$$
- $$\Rightarrow \hspace{0.3cm}K = \sqrt{K_2^2 + K_3^2 + K_4^2 +\text{...} } \approx 15 \%.$$
Im Kapitel Qualitätskriterien wurde gezeigt, dass damit auch das SNR $ρ_v = 1/K^2 ≈ 44$ festliegt. $ρ_v$ $($nicht aber $K)$ kann zudem auch dann als Qualitätskriterium herangezogen werden, wenn $q(t)$ mehr als eine Frequenz beinhaltet ⇒ Herleitung im Buch Lineare zeitinvariante Systeme.
Berücksichtigung von Kanalverzerrungen
Für die folgenden Betrachtungen setzen wir das Modulationsverfahren „ZSB–AM mit Träger” sowie ein cosinusförmiges Quellensignal $q(t)$ voraus. Die Amplituden von Nachrichten– und Trägersignal seien $A_{\rm N} = 4 \ \rm V$ und $A_{\rm T} = 5 \ \rm V $ ⇒ Modulationsgrad $m = 0.8$.
- Damit ist (ideale) Hüllkurvendemodulation prinzipiell anwendbar.
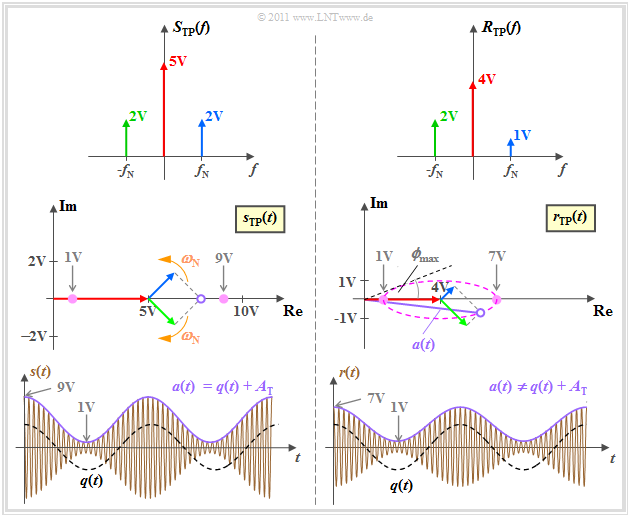
Die Grafik zeigt von oben nach unten
- die Spektren $S_{\rm TP}(f)$ und $R_{\rm TP}(f)$ des äquivalenten Tiefpass–Signals, die als reell angenommen werden,
- die äquivalenten Tiefpass–Signale $s_{\rm TP}(t)$ und $r_{\rm TP}(t)$ in der komplexen Ebene, und schließlich
- die physikalischen Signale $s(t)$ und $r(t)$.
Die linke Bildhälfte zeigt die Senderseite und gibt gleichzeitig die Verhältnisse am Empfänger bei idealem Kanal an.
- Wegen des Modulationsgrades $m ≤ 1$ erkennt man in der Hüllkurve $a(t)$ das Quellensignal $q(t)$.
- Demzufolge ist Hüllkurvendemodulation bei gewissen Voraussetzungen ohne Verzerrungen anwendbar, wie im $\text{Beispiel 4}$ gezeigt wird.
Die rechte Hälfte berücksichtigt unsymmetrische Verzerrungen durch den Kanal.
- Der Träger wird hier mit $α_{\rm T} = 0.8$ gedämpft, das obere Seitenband sogar mit $α_{\rm O} = 0.5$.
- Nun verläuft die Hüllkurve $a(t) ≠ q(t) + A_{\rm T}$ nicht mehr cosinusförmig.
- Eine Hüllkurvendemodulation führt hier zu nichtlinearen Verzerrungen wie im $\text{Beispiel 5}$ gezeigt.
$\text{Beispiel 4:}$ Es gelte weiterhin $A_{\rm N} = 4 \ \rm V$ und $A_{\rm T} = 5 \rm V$ ⇒ Modulationsgrad $m = 0.8$.
Die Grafik verdeutlicht den Einsatz eines idealen Hüllkurvendemodulators bei idealem Kanal, wobei folgende Identitäten berücksichtigt sind:
- $$R_{\rm TP}(f) \hspace{-0.05cm}=\hspace{-0.05cm} S_{\rm TP}(f) \hspace{0.02cm}, \hspace{0.15cm} r_{\rm TP}(t) \hspace{-0.05cm}=\hspace{-0.05cm} s_{\rm TP}(t) \hspace{0.02cm}, \hspace{0.15cm} r(t) \hspace{-0.05cm}=\hspace{-0.05cm} s(t) \hspace{0.02cm}.$$
Man erkennt aus diesen Darstellungen:
- Der den Träger beschreibende rote Zeiger der Länge $A_{\rm T}$ liegt fest.
- Das obere Seitenband (blau) dreht in mathematisch positiver Richtung, das untere Seitenband (grün) entgegengesetzt.
- Da der blaue und der grüne Zeiger beide mit der gleichen Winkelgeschwindigkeit $ω_{\rm N}$ drehen, aber in entgegengesetzte Richtungen, ist die vektorielle Summe aller Zeiger stets reell.
- Ist der Modulationsgrad $m ≤ 1$, so gilt für alle Zeiten $r_{\rm TP}(t) ≥ 0$ und $ϕ(t) = 0$. Das bedeutet, dass die Nulldurchgänge des Empfangssignals $r(t)$ genau mit denen des Trägersignals $z(t)$ übereinstimmen.
- Die Hüllkurve $a(t)$ des Signals $r(t)$ ist gleich der resultierenden Zeigerlänge, also gleich dem Betrag von $r_{\rm TP}(t)$. Wegen $m< 1$ gilt $a(t) = q(t) + A_{\rm T}$.
- Bei den gegebenen Amplitudenwerten liegt die Ortskurve $r_{\rm TP}(t)$ auf der reellen Achse zwischen den Endpunkten $A_{\rm T} \ – \ A_{\rm N} = 1\ \rm V$ und $A_{\rm T} + A_{\rm N} = 9 \ \rm V$.
- Die Ortskurve auf der reellen Achse in rechter Halbebene ist ein Indiz dafür, dass das Nachrichtensignal durch Hüllkurvendemodulation verzerrungsfrei möglich ist.
$\text{Beispiel 5:}$ Betrachten wir nun die gleichen Grafiken für den verzerrenden Kanal mit
- $α_{\rm U} = 1$ ⇒ das untere Seitenband (USB) wird nicht verändert,
- $α_{\rm T} = 0.8$ ⇒ der Träger wird etwas gedämpft,
- $α_{\rm U} = 0.5$ ⇒ das obere Seitenband (OSB) wird mehr gedämpft.
Die Grafiken lassen sich wie folgt interpretieren:
- Aufgrund der unterschiedlichen Längen von grünem Zeiger (USB) und blauem Zeiger (OSB) wird die Ortskurve zu einer Ellipse, deren Mittelpunkt durch den (roten) Träger festliegt.
- Der Winkel zwischen dem komplexwertigen $r_{\rm TP}(t)$ und dem Koordinatenursprung ist nun nicht mehr durchgängig $ϕ(t) = 0$, sondern schwankt zwischen $±ϕ_{\rm max}.$
- Die maximale Phase ist gleich dem Winkel der Tangente an die Ellipse. Im physikalischen Signal führt $ϕ(t) ≠ 0$ zu Verschiebungen der Nulldurchgänge von $r(t)$ gegenüber seinen Solllagen – vorgegeben durch das Trägersignal $z(t)$.
- Der Betrag $a(t) = \vert r_{\rm TP}(t) \vert$ – also die Hüllkurve von $r(t)$ – ist nun nicht mehr cosinusförmig und das Signal nach dem Hüllkurvendemodulator beinhaltet außer der Frequenz $f_{\rm N}$ auch Oberwellen:
$v(t) = A_{\rm 1} \cdot \cos(\omega_{\rm N}\cdot t ) +A_{\rm 2} \cdot \cos(2\omega_{\rm N}\cdot t )+A_{\rm 3} \cdot \cos(3\omega_{\rm N} \cdot t )+ \text{...}$ - Diese führen zu nichtlinearen Verzerrungen und werden durch den Klirrfaktor $K$ erfasst. Mit $A_{\rm N} = 4 \ \rm V$, $A_{\rm T} = 5 \ \rm V$, $α_{\rm U} = 1$ und $α_{\rm T} = 0.8$ ergeben sich in Abhängigkeit von $α_{\rm O}$ folgende Zahlkenwerte:
- $α_{\rm O} = 1.00$: $K = 0$ ⇒ lediglich der Träger wird gedämpft,
- $α_{\rm O} = 0.75$: $K ≈ 0.4\%$,
- $α_{\rm O} = 0.50$: $K ≈ 1.5\%$ ⇒ dieser Wert ist der Grafik zugrunde gelegt,
- $α_{\rm O} = 0.25$: $K ≈ 4\%$,
- $α_{\rm O} = 0.00$: $K ≈ 10\%$ ⇒ vollständige Unterdrückung des OSB.
Die Grafik gilt für $α_{\rm O} = 0.5$. Dann kommt es (allerdings ist beides mit dem bloßen Auge nur schwer zu erkennen)
- zu Verschiebungen der Nulldurchgänge im Signal $r(t)$ um maximal $25^\circ\hspace{-0.05cm}/360^\circ ≈ 7\%$ der Trägerperiode $T_0$, und
- zur Abweichung von der idealen Cosinusform ⇒ $K ≈ 1.5\%$ .
Symmetrische Kanalverzerrungen – Dämpfungsverzerrungen
Ein wesentliches Ergebnis des letzten Abschnitts war, dass es bei unsymmetrischen linearen Verzerrungen auf dem Kanal zu nichtlinearen Verzerrungen bezüglich des Nachrichtensignals kommt.
- Wird dagegen das untere Seitenband in gleicher Weise gedämpft wie das obere Seitenband, so ist die Ortskurve wieder eine horizontale Gerade und es entstehen keine nichtlinearen Verzerrungen.
- Vielmehr sind dann die Verzerrungen bezüglich $q(t)$ und $v(t)$ – ebenso wie die Verzerrungen bezüglich $s(t)$ und $r(t)$ – linear und können durch ein geeignet dimensioniertes Filter entzerrt werden.
Wir gehen hier von folgenden Voraussetzungen aus:
- Quellensignal $q(t)$ – bestehend aus zwei Cosinusanteilen bei den Frequenzen $f_1$ und $f_2$ mit den Amplituden $A_1$ und $A_2$;
- ZSB–AM mit Träger ⇒ das Sendesignal $s(t)$ setzt sich aus insgesamt fünf Cosinusschwingungen bei den Frequenzen $f_{\rm T}, f_{\rm T} ± f_1$ und $f_{\rm T} ± f_2$ zusammen;
- Kanal mit Dämpfungsverzerrungen, symmetrisch um die Trägerfrequenz:
- $$H_{\rm K} (f = f_{\rm T})= \alpha_0, \hspace{0.3cm} H_{\rm K} (f = \pm f_{\rm 1})= \alpha_1, \hspace{0.3cm}H_{\rm K} (f = \pm f_{\rm 2})= \alpha_2;$$
- Idealer Hüllkurvendemodulator gemäß der Beschreibung in diesem Abschnitt.
Die Grafik zeigt die Spektralfunktionen der äquivalenten Tiefpass–Signale von Sende– und Empfangssignal. Anhand dieses Bildes sind folgende Aussagen möglich:
- Das äquivalente Tiefpass–Signal $r_{\rm TP}(t)$ ist reell. Die Ortskurve – also die Spitze des Zeigerverbundes in der komplexen Ebene – liegt auch hier wieder auf der reellen Achse.
- Ist $α_0 · A_{\rm T}$ größer als $α_1 · A_1 + α_2 · A_2$, so ist der „Modulationsgrad des Empfangssignals” kleiner als $1$ und es kommt nicht zu nichtlinearen Verzerrungen.
- Das Sinkensignal nach idealer Hüllkurvendemodulation und Eliminierung des Gleichanteils $α_0 · A_{\rm T}$ durch den folgenden Hochpass lautet:
- $$v(t) = \alpha_1 \cdot A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) + \alpha_2 \cdot A_{\rm 2} \cdot \cos(2 \pi f_{\rm 2} t ) \hspace{0.05cm}.$$
Das bedeutet:
- Es kommt zu linearen Verzerrungen (Dämpfungsverzerrungen), falls $α_2 ≠ α_1$ ist.
- Wäre die Symmetrie bezüglich $f_{\rm T}$ nicht gegeben, so würden nichtlineare Verzerrungen entstehen.
Wir verweisen hier auf das Lernvideo Lineare und nichtlineare Verzerrungen.
Einfluss von additivem weißen Gaußschen Rauschen
Ausgehend von der Systemkonfiguration
- ZSB–Amplitudenmodulation mit Modulationsgrad $m ≤ 1$ sowie
- bestmöglich angepasste Hüllkurvendemodulation
wird nun der Einfluss von additivem Rauschen abgeschätzt. Verzerrungen jeglicher Art – beispielsweise bedingt durch einen ungeeigneten Kanal oder die nichtperfekte Realisierung von Modulator und Demodulator – werden ausgeschlossen.
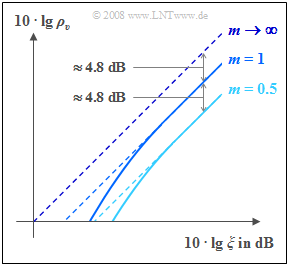
Die Grafik zeigt den Sinkenstörabstand $10 · \lg \, ρ_v$ bei unterschiedlichem Modulationsgrad $m$ in Abhängigkeit der logarithmierten Leistungskenngröße
- $$10 \cdot {\rm lg }\hspace{0.1cm} \xi = 10 \cdot {\rm lg }\hspace{0.1cm} \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \hspace{0.05cm}.$$
Das Ergebnis des Hüllkurvendemodulators ist mit durchgezogenen Linien markiert, während die gestrichelten Geraden den Synchrondemodulator kennzeichnen.
Wie bereits in Kapitel Untersuchungen im Hinblick auf Signalverzerrungen hergeleitet wurde, ergeben sich für den Synchrondemodulator $\rm (SD)$ in dieser doppelt–logarithmischen Darstellung
- die Winkelhalbierende (für $m → ∞$, ZSB–AM ohne Träger), bzw.
- hierzu parallel verschobene Gerade mit vertikalem Abstand $10 · \lg \, (1 + 2/m^2$).
Bei Anwendung von Hüllkurvendemodulation $\rm (HKD)$ sind folgende Unterschiede festzustellen:
- Ein Hüllkurvendemodulator ist für $m > 1$ nicht sinnvoll. Dadurch würden starke nichtlineare Verzerrungen entstehen.
- Die durchgehend gezeichneten $\rm HKD$–Kurven liegen stets unterhalb der gestrichelten $\rm SD$–Geraden, wenn man vom gleichen Modulationsgrad $m$ ausgeht.
- Ab einem gewissen Wert der Leistungskenngröße $ξ$ sind allerdings die $\rm HKD$–Kurven von den $\rm SD$–Geraden innerhalb der Zeichengenauigkeit nicht mehr zu unterscheiden.
Mehr Informationen zu dieser Thematik finden Sie beispielsweise in [Kam 04][1].
Argumente für und gegen den Hüllkurvendemodulator
Der wichtigste Grund für die Verwendung des Hüllkurvendemodulators ist (besser gesagt: war), dass damit die oft aufwändige Frequenz– und Phasensynchronisation vermieden wurde, so dass dieser preisgünstig realisiert werden konnte. Der Hüllkurvendemodulator ist somit ein Beispiel eines "inkohärenten Demodulators".
Für den Synchrondemodulator und gegen den Hüllkurvendemodulator können dagegen mehrere Gründe angeführt werden:
- Bei Hüllkurvendemodulation muss eine Übermodulation $(m > 1)$ unter allen Umständen vermieden werden. Dies erreicht man beispielsweise durch die Amplitudenbegrenzung des Quellensignals, was aber ebenfalls nichtlineare Verzerrungen zur Folge hat.
- Bei sonst gleichen Randbedingungen ist ein Modulationsgrad $m < 1$ nur durch die Erhöhung der Sendeleistung um mindestens den Faktor $3$ zu erreichen. Dies ist auch wegen der berechtigten Diskussionen zum Thema „Elektro-Smog” in großen Teilen unserer Gesellschaft problematisch.
- Lineare Kanalverzerrungen können bei einem Hüllkurvendemodulator zu irreversiblen nichtlinearen Verzerrungen führen, während die bei Synchrondemodulation entstehenden linearen Verzerrungen möglicherweise durch besondere Maßnahmen beim Empfänger kompensiert werden können.
Aufgaben zum Kapitel
Aufgabe 2.7: Ist der Modulationsgrad zu groß?
Aufgabe 2.7Z: ZSB-AM und Hüllkurvendemodulator
Aufgabe 2.8: Unsymmetrischer Kanal
Aufgabe 2.9: Symmetrische Verzerrungen
Quellenverzeichnis
- ↑ Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.