Aufgaben:Aufgabe 5.6: OFDM–Spektrum: Unterschied zwischen den Versionen
K (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1659__A_5_6.png|right|frame|Real | + | [[Datei:P_ID1659__A_5_6.png|right|frame|Real– und Imaginärteil des OFDM–Signals]] |
| − | Wir betrachten | + | Wir betrachten in dieser Aufgabe ein OFDM–System mit $N = 4$ Trägern. |
| + | *Zur Vereinfachung beschränken wir uns auf ein einziges Zeitintervall $T$. | ||
| + | *Die Rahmendauer ist ebenfalls $T_{\rm R} = T.$ | ||
| + | *Ein Guard–Intervall wird demnach nicht verwendet. | ||
| + | |||
Mit der Zusammenfassung von Impulsformung und Modulation durch die gemeinsame Funktion | Mit der Zusammenfassung von Impulsformung und Modulation durch die gemeinsame Funktion | ||
:$$ g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm sonst} \\ \end{array} \right.$$ | :$$ g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm sonst} \\ \end{array} \right.$$ | ||
| − | ergibt sich das (komplexe) OFDM–Sendesignal im betrachteten Zeitintervall ( | + | ergibt sich das (komplexe) OFDM–Sendesignal im betrachteten Zeitintervall $(0 ≤ t < T)$ zu: |
:$$ s (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu} \cdot g_\mu (t )}.$$ | :$$ s (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu} \cdot g_\mu (t )}.$$ | ||
| − | Alle Trägerkoeffizienten $a_0$, $a_1$, $a_2$ | + | Alle Trägerkoeffizienten $a_0$, $a_1$, $a_2$, $a_3$ sind entweder $0$ oder $\pm 1$. |
| + | |||
| + | Die Grafik zeigt den Real– und Imaginärteil des Sendesignals $s(t)$ für eine gegebene Kombination von $a_0$, ... , $a_3$, <br>die in der Teilaufgabe '''(3)''' ermittelt werden soll. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Allgemeine_Beschreibung_von_OFDM|Allgemeine Beschreibung von OFDM]]. | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Allgemeine_Beschreibung_von_OFDM|Allgemeine Beschreibung von OFDM]]. |
| − | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Allgemeine_Beschreibung_von_OFDM#Das_Prinzip_von_OFDM_.E2.80.93_Systembetrachtung_im_Zeitbereich|OFDM-Systembetrachtung im Zeitbereich]] | + | *Bezug genommen wird insbesondere auf die Seiten |
| + | : [[Modulationsverfahren/Allgemeine_Beschreibung_von_OFDM#Das_Prinzip_von_OFDM_.E2.80.93_Systembetrachtung_im_Zeitbereich|OFDM-Systembetrachtung im Zeitbereich]], | ||
| + | : [[Modulationsverfahren/Allgemeine_Beschreibung_von_OFDM#Systembetrachtung_im_Frequenzbereich_bei_kausalem_Grundimpuls|OFDM-Systembetrachtung im Frequenzbereich bei kausalem Grundimpuls]]. | ||
| Zeile 22: | Zeile 34: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die Amplitude $s_0$ des Sendesignals? | + | {Wie groß ist die Amplitude $s_0$ des Sendesignals? |
|type="{}"} | |type="{}"} | ||
$s_0 \ = \ $ { 5 3% } $\ \rm V$ | $s_0 \ = \ $ { 5 3% } $\ \rm V$ | ||
| − | {Wie groß ist die Symboldauer | + | {Wie groß ist die Symboldauer $T$? |
|type="{}"} | |type="{}"} | ||
$T \ = \ $ { 0.2 3% } $\ \rm ms$ | $T \ = \ $ { 0.2 3% } $\ \rm ms$ | ||
| Zeile 37: | Zeile 49: | ||
$a_3 \ = \ ${ -1.01--0.99 } | $a_3 \ = \ ${ -1.01--0.99 } | ||
| − | {Welche Aussagen sind bezüglich der OFDM–Betragsfunktion | | + | {Welche Aussagen sind bezüglich der OFDM–Betragsfunktion $|s(t)|$ zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | - $|s(t)|$ ist konstant ohne Begrenzung. | + | - $|s(t)|$ ist konstant ohne Begrenzung. |
| − | + $|s(t)|$ ist konstant innerhalb | + | + $|s(t)|$ ist konstant innerhalb der Symboldauer $T$. |
| − | - $|s(t)|$ besitzt einen cosinusförmigen Verlauf. | + | - $|s(t)|$ besitzt einen cosinusförmigen Verlauf. |
| − | - $|s(t)|$ besitzt einen sinusförmigen Verlauf. | + | - $|s(t)|$ besitzt einen sinusförmigen Verlauf. |
| − | {Nun sei $a_0 = 0$, $a_1 = +1$, $a_2 = -1$ | + | {Nun sei $a_0 = 0$, $a_1 = +1$, $a_2 = -1$, $a_3 = +1$. Berechnen Sie das Spektrum $S(f)$. Welche Werte ergeben sich für die genannten Frequenzen? |
| − | |||
|type="{}"} | |type="{}"} | ||
$S(f = 0)\ = \ $ { 0. } $\ \rm mV/Hz$ | $S(f = 0)\ = \ $ { 0. } $\ \rm mV/Hz$ | ||
| Zeile 52: | Zeile 63: | ||
$S(f = 15 \ \rm kHz) \ = \ $ { 1 1% } $\ \rm mV/Hz$ | $S(f = 15 \ \rm kHz) \ = \ $ { 1 1% } $\ \rm mV/Hz$ | ||
| − | {Interpretieren Sie Ihre Ergebnisse der Teilaufgaben (3) und (5). Welche Aussagen treffen zu? | + | {Interpretieren Sie Ihre Ergebnisse der Teilaufgaben '''(3)''' und '''(5)'''. Welche Aussagen treffen zu? |
|type="[]"} | |type="[]"} | ||
+ OFDM erfüllt das erste Nyquist–Kriterium im Zeitbereich. | + OFDM erfüllt das erste Nyquist–Kriterium im Zeitbereich. | ||
| Zeile 60: | Zeile 71: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Das Sendesignal $s(t)$ ist eine komplexe | + | '''(1)''' Das Sendesignal $s(t)$ ist eine komplexe Schwingung mit nur einer Frequenz. |
| + | *Die Amplitude $s_0 \hspace{0.15cm}\underline { = 5\ \rm V}$ kann direkt der Grafik entnommen werden. | ||
| + | |||
| − | '''(2)''' Weiterhin erkennt man aus der Grafik die Symboldauer $T\hspace{0.15cm}\underline { = 0.2\ \rm ms}$. Daraus ergibt sich die Grundfrequenz zu $f_0 = 1/T = 5\ \rm kHz$. | + | '''(2)''' Weiterhin erkennt man aus der Grafik die Symboldauer $T\hspace{0.15cm}\underline { = 0.2\ \rm ms}$. |
| + | *Daraus ergibt sich die Grundfrequenz zu $f_0 = 1/T = 5\ \rm kHz$. | ||
| − | '''(3)''' Im dargestellten Beispiel gibt es nur eine einzige Frequenz $3 · f_0$. Daraus folgt $a_0 = a_1 = a_2 \hspace{0.15cm}\underline { = 0}$ sowie für den Bereich $0 ≤ t < T$: | + | |
| + | '''(3)''' Im dargestellten Beispiel gibt es nur eine einzige Frequenz, nämlich $3 · f_0$. | ||
| + | *Daraus folgt $a_0 = a_1 = a_2 \hspace{0.15cm}\underline { = 0}$ sowie für den Bereich $0 ≤ t < T$: | ||
:$$s(t) = a_3 \cdot s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2 \pi}} \hspace{0.04cm}\cdot \hspace{0.04cm} 3 f_0 \hspace{0.04cm}\cdot \hspace{0.04cm} t}= a_3 \cdot s_0 \cdot \cos ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \rm{j} \cdot a_3 \cdot s_0 \cdot \sin ({\rm{2 \pi}} \cdot 3 f_0 \cdot t).$$ | :$$s(t) = a_3 \cdot s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2 \pi}} \hspace{0.04cm}\cdot \hspace{0.04cm} 3 f_0 \hspace{0.04cm}\cdot \hspace{0.04cm} t}= a_3 \cdot s_0 \cdot \cos ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \rm{j} \cdot a_3 \cdot s_0 \cdot \sin ({\rm{2 \pi}} \cdot 3 f_0 \cdot t).$$ | ||
| − | Der Vergleich mit der Skizze (Realteil: Minus–Cosinus, Imaginärteil: Minus–Sinus) liefert das folgende Ergebnis: $a_3\hspace{0.15cm}\underline {= -1}$ | + | *Der Vergleich mit der Skizze $($Realteil: Minus–Cosinus, Imaginärteil: Minus–Sinus$)$ liefert das folgende Ergebnis: |
| + | :$$a_3\hspace{0.15cm}\underline {= -1}.$$ | ||
'''(4)''' Richtig ist der <u>zweite Lösungsvorschlag</u>: | '''(4)''' Richtig ist der <u>zweite Lösungsvorschlag</u>: | ||
* Die Betragsfunktion lautet: $ |s(t)| = a_3 \cdot s_0 \cdot \sqrt{\cos^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \sin^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t)}= a_3 \cdot s_0.$ | * Die Betragsfunktion lautet: $ |s(t)| = a_3 \cdot s_0 \cdot \sqrt{\cos^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \sin^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t)}= a_3 \cdot s_0.$ | ||
| − | *Allerdings gilt diese Gleichung nur im Bereich der Symboldauer $T$. Das OFDM–Prinzip funktioniert nur bei einer Zeitbegrenzung auf | + | *Allerdings gilt diese Gleichung nur im Bereich der Symboldauer $T$. |
| + | *Das bedeutet: Das OFDM–Prinzip funktioniert nur bei einer Zeitbegrenzung auf $T$. | ||
| + | |||
'''(5)''' Allgemein gilt für das OFDM–Spektrum: | '''(5)''' Allgemein gilt für das OFDM–Spektrum: | ||
:$$S (f) = s_0 \cdot T \cdot \sum\limits_{\mu = 0}^{N - 1} {a_{\mu } \cdot \,} {\rm{si}}(\pi \cdot T \cdot (f - \mu \cdot f_0 )) \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi}} \hspace{0.04cm}\cdot \hspace{0.04cm}{T}/{2}\hspace{0.04cm}\cdot \hspace{0.04cm} (f - \mu \cdot f_0 )} .$$ | :$$S (f) = s_0 \cdot T \cdot \sum\limits_{\mu = 0}^{N - 1} {a_{\mu } \cdot \,} {\rm{si}}(\pi \cdot T \cdot (f - \mu \cdot f_0 )) \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi}} \hspace{0.04cm}\cdot \hspace{0.04cm}{T}/{2}\hspace{0.04cm}\cdot \hspace{0.04cm} (f - \mu \cdot f_0 )} .$$ | ||
| − | *Die | + | *Die $\rm si$–Funktion ergibt sich aus der zeitlichen Begrenzung auf $T$, der letzte Term in der Summe aus dem Verschiebungssatz. |
| − | *Durch die Nulldurchgänge der | + | *Durch die Nulldurchgänge der $\rm si$–Funktion im Abstand $f_0$ sowie $\rm si(0) = 1$ erhält man |
| − | *Mit $s_0 = 5 \ \rm V$ und $T = 0.2 \ \rm ms$ ⇒ $s_0 · T = 1\ \rm mV/Hz$ gilt weiter: | + | :$$S(f = μ · f_0) = s_0 · T · a_μ.$$ |
| − | :$$ \mu = 0,\hspace{0.1cm} a_0 = 0 : S (f = 0) \hspace{0.15cm}\underline {= 0},\hspace{8cm}.$$ | + | *Mit $s_0 = 5 \ \rm V$ und $T = 0.2 \ \rm ms$ ⇒ $s_0 · T = 1\ \rm mV/Hz$ gilt weiter: |
| − | :$$\mu = 1, \hspace{0.1cm}a_1 = +1 : S (f = 5\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= +1\,\,{\rm{mV/Hz}}},$$ | + | :$$ \mu = 0,\hspace{0.1cm} a_0 = 0\text{:}\hspace{0.95cm} S (f = 0) \hspace{0.15cm}\underline {= 0},\hspace{8cm}.$$ |
| − | :$$ \mu = 2, \hspace{0.1cm}a_2 = -1 : S (f = 10\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= -1\,\,{\rm{mV/Hz}}},$$ | + | :$$\mu = 1, \hspace{0.1cm}a_1 = +1\text{:}\hspace{0.55cm} S (f = 5\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= +1\,\,{\rm{mV/Hz}}},$$ |
| − | :$$ \mu = 3, \hspace{0.1cm}a_3 = +1 : S (f = 15\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= +1\,\,{\rm{mV/Hz}}}.$$ | + | :$$ \mu = 2, \hspace{0.1cm}a_2 = -1\text{:}\hspace{0.55cm} S (f = 10\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= -1\,\,{\rm{mV/Hz}}},$$ |
| + | :$$ \mu = 3, \hspace{0.1cm}a_3 = +1\text{:}\hspace{0.55cm} S (f = 15\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= +1\,\,{\rm{mV/Hz}}}.$$ | ||
| + | |||
'''(6)''' <u>Beide Aussagen</u> sind richtig: | '''(6)''' <u>Beide Aussagen</u> sind richtig: | ||
| − | * Die Orthogonalität bezüglich des Frequenzbereichs wurde bereits in der Teilaufgabe (5) gezeigt. | + | * Die Orthogonalität bezüglich des Frequenzbereichs wurde bereits in der Teilaufgabe '''(5)''' gezeigt. |
| − | *Die Orthogonalität hinsichtlich des Zeitbereichs ergibt sich aus der Begrenzung der einzelnen Symbole auf die Zeitdauer $T$. | + | *Die Orthogonalität hinsichtlich des Zeitbereichs ergibt sich aus der Begrenzung der einzelnen Symbole auf die Zeitdauer $T$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 10. Januar 2022, 11:29 Uhr
Wir betrachten in dieser Aufgabe ein OFDM–System mit $N = 4$ Trägern.
- Zur Vereinfachung beschränken wir uns auf ein einziges Zeitintervall $T$.
- Die Rahmendauer ist ebenfalls $T_{\rm R} = T.$
- Ein Guard–Intervall wird demnach nicht verwendet.
Mit der Zusammenfassung von Impulsformung und Modulation durch die gemeinsame Funktion
- $$ g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm sonst} \\ \end{array} \right.$$
ergibt sich das (komplexe) OFDM–Sendesignal im betrachteten Zeitintervall $(0 ≤ t < T)$ zu:
- $$ s (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu} \cdot g_\mu (t )}.$$
Alle Trägerkoeffizienten $a_0$, $a_1$, $a_2$, $a_3$ sind entweder $0$ oder $\pm 1$.
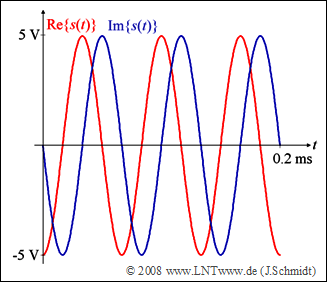
Die Grafik zeigt den Real– und Imaginärteil des Sendesignals $s(t)$ für eine gegebene Kombination von $a_0$, ... , $a_3$,
die in der Teilaufgabe (3) ermittelt werden soll.
Hinweise:
- Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung von OFDM.
- Bezug genommen wird insbesondere auf die Seiten
- OFDM-Systembetrachtung im Zeitbereich,
- OFDM-Systembetrachtung im Frequenzbereich bei kausalem Grundimpuls.
Fragebogen
Musterlösung
- Die Amplitude $s_0 \hspace{0.15cm}\underline { = 5\ \rm V}$ kann direkt der Grafik entnommen werden.
(2) Weiterhin erkennt man aus der Grafik die Symboldauer $T\hspace{0.15cm}\underline { = 0.2\ \rm ms}$.
- Daraus ergibt sich die Grundfrequenz zu $f_0 = 1/T = 5\ \rm kHz$.
(3) Im dargestellten Beispiel gibt es nur eine einzige Frequenz, nämlich $3 · f_0$.
- Daraus folgt $a_0 = a_1 = a_2 \hspace{0.15cm}\underline { = 0}$ sowie für den Bereich $0 ≤ t < T$:
- $$s(t) = a_3 \cdot s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2 \pi}} \hspace{0.04cm}\cdot \hspace{0.04cm} 3 f_0 \hspace{0.04cm}\cdot \hspace{0.04cm} t}= a_3 \cdot s_0 \cdot \cos ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \rm{j} \cdot a_3 \cdot s_0 \cdot \sin ({\rm{2 \pi}} \cdot 3 f_0 \cdot t).$$
- Der Vergleich mit der Skizze $($Realteil: Minus–Cosinus, Imaginärteil: Minus–Sinus$)$ liefert das folgende Ergebnis:
- $$a_3\hspace{0.15cm}\underline {= -1}.$$
(4) Richtig ist der zweite Lösungsvorschlag:
- Die Betragsfunktion lautet: $ |s(t)| = a_3 \cdot s_0 \cdot \sqrt{\cos^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \sin^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t)}= a_3 \cdot s_0.$
- Allerdings gilt diese Gleichung nur im Bereich der Symboldauer $T$.
- Das bedeutet: Das OFDM–Prinzip funktioniert nur bei einer Zeitbegrenzung auf $T$.
(5) Allgemein gilt für das OFDM–Spektrum:
- $$S (f) = s_0 \cdot T \cdot \sum\limits_{\mu = 0}^{N - 1} {a_{\mu } \cdot \,} {\rm{si}}(\pi \cdot T \cdot (f - \mu \cdot f_0 )) \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi}} \hspace{0.04cm}\cdot \hspace{0.04cm}{T}/{2}\hspace{0.04cm}\cdot \hspace{0.04cm} (f - \mu \cdot f_0 )} .$$
- Die $\rm si$–Funktion ergibt sich aus der zeitlichen Begrenzung auf $T$, der letzte Term in der Summe aus dem Verschiebungssatz.
- Durch die Nulldurchgänge der $\rm si$–Funktion im Abstand $f_0$ sowie $\rm si(0) = 1$ erhält man
- $$S(f = μ · f_0) = s_0 · T · a_μ.$$
- Mit $s_0 = 5 \ \rm V$ und $T = 0.2 \ \rm ms$ ⇒ $s_0 · T = 1\ \rm mV/Hz$ gilt weiter:
- $$ \mu = 0,\hspace{0.1cm} a_0 = 0\text{:}\hspace{0.95cm} S (f = 0) \hspace{0.15cm}\underline {= 0},\hspace{8cm}.$$
- $$\mu = 1, \hspace{0.1cm}a_1 = +1\text{:}\hspace{0.55cm} S (f = 5\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= +1\,\,{\rm{mV/Hz}}},$$
- $$ \mu = 2, \hspace{0.1cm}a_2 = -1\text{:}\hspace{0.55cm} S (f = 10\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= -1\,\,{\rm{mV/Hz}}},$$
- $$ \mu = 3, \hspace{0.1cm}a_3 = +1\text{:}\hspace{0.55cm} S (f = 15\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= +1\,\,{\rm{mV/Hz}}}.$$
(6) Beide Aussagen sind richtig:
- Die Orthogonalität bezüglich des Frequenzbereichs wurde bereits in der Teilaufgabe (5) gezeigt.
- Die Orthogonalität hinsichtlich des Zeitbereichs ergibt sich aus der Begrenzung der einzelnen Symbole auf die Zeitdauer $T$.