Aufgaben:Aufgabe 5.9: Wahl der OFDM–Parameter: Unterschied zwischen den Versionen
K (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1668__Mod_A_5_9.png|right|frame|Zeitabhängiger Dämfungsverlauf zweier Mobilfunkkanäle]] | + | [[Datei:P_ID1668__Mod_A_5_9.png|right|frame|Zeitabhängiger Dämfungsverlauf <br>zweier Mobilfunkkanäle]] |
| − | In dieser Aufgabe sollen einige OFDM–Parameter eines Mobilfunksystems bestimmt werden. | + | In dieser Aufgabe sollen einige OFDM–Parameter eines Mobilfunksystems bestimmt werden. |
| − | |||
| − | |||
| − | |||
| − | |||
| + | Dabei wird von folgenden Voraussetzungen ausgegangen: | ||
| + | * Die Kohärenzzeit des Kanals ist $T_{\rm coh} = 0.4 \ \rm ms$. | ||
| + | * Die maximale Pfadverzögerung sei $τ_{\rm max} = 25 \ \rm µ s$. | ||
| + | * Die Datenrate (Bitrate) beträgt $R_{\rm B} = 1 \ \rm Mbit/s$. | ||
| + | * Alle Unterträger werden $\rm 4–QAM$–moduliert. | ||
| − | Um eine gewisse Robustheit des Systems gegenüber zeit– und frequenzselektivem Fading zu gewährleisten, muss die folgende Ungleichung erfüllt werden: | + | |
| + | Um eine gewisse Robustheit des Systems gegenüber zeit– und frequenzselektivem Fading zu gewährleisten, muss die folgende Ungleichung erfüllt werden: | ||
:$$T_{\rm{G}} \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}.$$ | :$$T_{\rm{G}} \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}.$$ | ||
Insgesamt soll folgendermaßen vorgegangen werden: | Insgesamt soll folgendermaßen vorgegangen werden: | ||
| − | * Vorläufige Festlegung des Guard–Intervalls ( | + | * Vorläufige Festlegung des Guard–Intervalls $(T_{\rm G}')$, |
| − | * Bestimmung der optimalen Kernsymboldauer $T$, | + | * Bestimmung der optimalen Kernsymboldauer $(T)$, |
| − | * entsprechende Festlegung der Stützstellenzahl der FFT. | + | * entsprechende Festlegung der Stützstellenzahl der $\rm FFT$. |
| − | Danach ist eventuell eine erneute Bestimmung einiger Systemgrößen aufgrund der bei den Berechnungen | + | |
| + | Danach ist eventuell eine erneute Bestimmung einiger Systemgrößen aufgrund der bei den Berechnungen vorgenommenen Rundungen erforderlich. | ||
Die Grafik zeigt zwei beispielhafte Dämpfungsverläufe von Mobilfunksystemen in logarithmischer Darstellung. | Die Grafik zeigt zwei beispielhafte Dämpfungsverläufe von Mobilfunksystemen in logarithmischer Darstellung. | ||
| − | *Bei der blauen Kurve geschehen die zeitlichen Veränderungen relativ langsam, bei der roten Kurve viermal so schnell. | + | *Bei der blauen Kurve geschehen die zeitlichen Veränderungen relativ langsam, bei der roten Kurve viermal so schnell. |
| − | *Demzufolge weist der blaue Kanal eine viermal größere Kohärenzzeit als der rote Kanal | + | *Demzufolge weist der blaue Kanal eine viermal größere Kohärenzzeit auf als der rote Kanal. |
| + | |||
| + | |||
| − | + | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/OFDM_für_4G–Netze|OFDM für 4G–Netze]]. | + | Hinweise: |
| − | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/OFDM_für_4G–Netze#Bestimmung_einiger_OFDM.E2.80.93Parameter|Bestimmung einiger OFDM-Parameter]]. | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/OFDM_für_4G–Netze|OFDM für 4G–Netze]]. |
| − | * Weitere Informationen zum Thema finden Sie im LNTwww–Buch [[Mobile Kommunikation]]. | + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/OFDM_für_4G–Netze#Bestimmung_einiger_OFDM.E2.80.93Parameter|Bestimmung einiger OFDM-Parameter]]. |
| + | * Weitere Informationen zum Thema finden Sie im LNTwww–Buch [[Mobile Kommunikation]]. | ||
| Zeile 37: | Zeile 43: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Bestimmen Sie die minimal sinnvolle Dauer $T_{\rm G}'$ des „vorläufigen Guard–Intervalls”. | + | {Bestimmen Sie die minimal sinnvolle Dauer $T_{\rm G}'$ des „vorläufigen Guard–Intervalls”. |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm G}' \ = \ $ { 25 3% } $\ \rm | + | $T_{\rm G}' \ = \ $ { 25 3% } $\ \rm µ s$ |
| − | {Bestimmen Sie die optimale Kernsymboldauer $T_{\rm opt}$ als geometrisches Mittel. | + | {Bestimmen Sie die optimale Kernsymboldauer $T_{\rm opt}$ als geometrisches Mittel. |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm opt} \ = \ $ { 97 3% } $\ \rm | + | $T_{\rm opt} \ = \ $ { 97 3% } $\ \rm µ s$ |
| Zeile 54: | Zeile 60: | ||
$N_{\rm FFT} \ = \ $ { 64 1% } | $N_{\rm FFT} \ = \ $ { 64 1% } | ||
| − | {Berechnen Sie die Anzahl $N_{\rm G}$ der Zeitabtastwerte des Guard–Intervalls und daraus die neue resultierende Schutzzeit $T_{\rm G}$. | + | {Berechnen Sie die Anzahl $N_{\rm G}$ der Zeitabtastwerte des Guard–Intervalls und daraus die neue resultierende Schutzzeit $T_{\rm G}$. |
|type="{}"} | |type="{}"} | ||
$N_{\rm G} \ = \ $ { 17 1% } | $N_{\rm G} \ = \ $ { 17 1% } | ||
| − | $T_{\rm G} \ = \ $ { 26 1% } $\ \rm | + | $T_{\rm G} \ = \ $ { 26 1% } $\ \rm µ s$ |
| − | {Geben Sie nun anhand Ihrer Berechnungen die Dauer $T_{\rm R}$ eines Rahmens an | + | {Geben Sie nun anhand Ihrer Berechnungen die Dauer $T_{\rm R}$ eines Rahmens an. |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm R} \ = \ $ { 123 1% } $\ \rm | + | $T_{\rm R} \ = \ $ { 123 1% } $\ \rm µ s$ |
{Wie groß ist die Anzahl der insgesamt in einem Rahmen enthaltenen Abtastwerte? | {Wie groß ist die Anzahl der insgesamt in einem Rahmen enthaltenen Abtastwerte? | ||
| Zeile 67: | Zeile 73: | ||
$N_{\rm gesamt} \ = \ $ { 81 1% } | $N_{\rm gesamt} \ = \ $ { 81 1% } | ||
| − | {Ermitteln Sie mit den bestimmten Parametern die Nutzträgeranzahl $N_{\rm Nutz}'$ erneut. | + | {Ermitteln Sie mit den bestimmten Parametern die Nutzträgeranzahl $N_{\rm Nutz}'$ erneut. |
|type="{}"} | |type="{}"} | ||
$N_{\rm Nutz}' \ = \ $ { 62 1% } | $N_{\rm Nutz}' \ = \ $ { 62 1% } | ||
| Zeile 74: | Zeile 80: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Es gilt $T_{\rm G}' = \tau_{\rm max} \hspace{0.15cm}\underline { = 25\ \rm µ s}$. |
| + | *Damit ist die untere Grenze der Ungleichung $T_{\rm{G}}' \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}'$ festgelegt. | ||
| + | *Aber auch die obere Grenze lässt sich nun berechnen, da die Kohärenzzeit $T_{\rm coh} = 400\ \rm µ s$ bekannt ist. | ||
| − | '''(2)''' Zur sinnvollen Lösung der Ungleichung aus (1) wird das geometrische Mittel verwendet: | + | |
| − | :$$T_{{\rm{opt}}} = \sqrt {T_{\rm{G}} ' \cdot (T_{{\rm{coh}}} - T_{\rm{G}} ')} = \sqrt {{25\,\,{\rm | + | '''(2)''' Zur sinnvollen Lösung der Ungleichung aus '''(1)''' wird das geometrische Mittel verwendet: |
| + | :$$T_{{\rm{opt}}} = \sqrt {T_{\rm{G}} ' \cdot (T_{{\rm{coh}}} - T_{\rm{G}} ')} = \sqrt {{25\,\,{\rm µ s}} \cdot ({400\,\,{\rm µ s}} - {25\,\,{\rm µ s}})} \hspace{0.15cm}\underline { \approx {97\,\,{\rm µ s}}}.$$ | ||
| + | |||
'''(3)''' Die benötigte Anzahl der Nutzträger ergibt sich aus folgender Gleichung: | '''(3)''' Die benötigte Anzahl der Nutzträger ergibt sich aus folgender Gleichung: | ||
:$$N_{{\rm{Nutz}}} = \left\lceil {\frac{{R_{{\rm{B}}} \cdot (T + T_{\rm{G}} ')}} {{{\rm{log}_2}(M)}}}\right\rceil | :$$N_{{\rm{Nutz}}} = \left\lceil {\frac{{R_{{\rm{B}}} \cdot (T + T_{\rm{G}} ')}} {{{\rm{log}_2}(M)}}}\right\rceil | ||
| − | = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm | + | = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm µ s}} + {25\,\,{\rm µ s}} )} |
{{{\rm{log}_2}(4)}}}\right\rceil\hspace{0.15cm}\underline {= 61}.$$ | {{{\rm{log}_2}(4)}}}\right\rceil\hspace{0.15cm}\underline {= 61}.$$ | ||
| − | '''(4)''' Die Stützstellenzahl der FFT muss stets eine Zweier–Potenz sein. Daraus folgt: | + | |
| + | '''(4)''' Die Stützstellenzahl der $\rm FFT$ muss stets eine Zweier–Potenz sein. Daraus folgt: | ||
:$$ N_{{\rm{FFT}}} = 2^{\left\lceil {{\rm{log_2}} \hspace{0.05cm}(61 )} \right\rceil } = 2^6\hspace{0.15cm}\underline {= 64}.$$ | :$$ N_{{\rm{FFT}}} = 2^{\left\lceil {{\rm{log_2}} \hspace{0.05cm}(61 )} \right\rceil } = 2^6\hspace{0.15cm}\underline {= 64}.$$ | ||
| − | Ungenutzte Träger können an den Rändern des Spektrums als Guard–Band verwendet werden. | + | *Ungenutzte Träger können an den Rändern des Spektrums als Guard–Band verwendet werden. |
| − | '''(5)''' Wir bezeichnen die gerundete Anzahl der Stützstellen des Guardintervalls mit $N_{\rm{G}}$ | + | '''(5)''' Wir bezeichnen die gerundete Anzahl der Stützstellen des Guardintervalls mit $N_{\rm{G}}$. Dann gilt: |
| − | :$$N_{\rm{G}} = \left\lceil {\frac{{T_{\rm{G}} '}} {{T_{{\rm{opt}}} }} \cdot N_{{\rm{FFT}}} } \right\rceil = \left\lceil {\frac{25\,\,{\rm | + | :$$N_{\rm{G}} = \left\lceil {\frac{{T_{\rm{G}} '}} {{T_{{\rm{opt}}} }} \cdot N_{{\rm{FFT}}} } \right\rceil = \left\lceil {\frac{25\,\,{\rm µ s}} {97\,\,{\rm µ s}} \cdot 64 } \right\rceil \hspace{0.15cm}\underline {= 17},$$ |
| − | :$$ T_{\rm{G}} = N_{\rm{G}} \cdot \frac{{T_{{\rm{opt}}} }} {{N_{{\rm{FFT}}} }}= 17 \cdot \frac{{97\,\,{\rm | + | :$$ T_{\rm{G}} = N_{\rm{G}} \cdot \frac{{T_{{\rm{opt}}} }} {{N_{{\rm{FFT}}} }}= 17 \cdot \frac{{97\,\,{\rm µ s}}} {64}\hspace{0.15cm}\underline { \approx {26\,\,{\rm µ s}}}.$$ |
| + | |||
'''(6)''' Die Rahmendauer ergibt sich zu | '''(6)''' Die Rahmendauer ergibt sich zu | ||
| − | :$$T_{\rm{R}} = T + T_{\rm{G}} = {97\,\,{\rm | + | :$$T_{\rm{R}} = T + T_{\rm{G}} = {97\,\,{\rm µ s}} + {26\,\,{\rm µ s}}\hspace{0.15cm}\underline {= {123\,\,{\rm µ s}}}.$$ |
| − | '''(7)''' Mit den Ergebnissen der Teilaufgaben (4) und (5) erhält man: | + | |
| + | '''(7)''' Mit den Ergebnissen der Teilaufgaben '''(4)''' und '''(5)''' erhält man: | ||
:$$ N_{\rm{gesamt}} = N_{\rm{FFT}} + N_{\rm{G}} = 64 + 17 \hspace{0.15cm}\underline {= 81}.$$ | :$$ N_{\rm{gesamt}} = N_{\rm{FFT}} + N_{\rm{G}} = 64 + 17 \hspace{0.15cm}\underline {= 81}.$$ | ||
| − | '''(8)''' Die Neuberechnung ist nötig, da sich die Dauer des Guard–Intervalls geändert haben kann. Gegenüber der | + | |
| − | :$$N_ | + | '''(8)''' Die Neuberechnung ist nötig, da sich die Dauer des Guard–Intervalls geändert haben kann. |
| − | Damit ergibt sich aber weiterhin $N_{\rm FFT} = 64$. | + | *Gegenüber der Teilaufgab e '''(3)''' wird die vorläufige Länge $T_{\rm{G}} '$ durch $T_{\rm{G}} $ ersetzt und man erhält ein geringfügig anderes Ergebnis: |
| + | :$$N_{\rm Nutz}' = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm µ s}} + {26\,\,{\rm µ s}} )} {{{\rm{log_2}}(4)}}}\right\rceil = \left\lceil 61.5\right\rceil\hspace{0.15cm}\underline {= 62}.$$ | ||
| + | *Damit ergibt sich aber weiterhin $N_{\rm FFT} = 64$. | ||
Aktuelle Version vom 25. Januar 2022, 12:16 Uhr
In dieser Aufgabe sollen einige OFDM–Parameter eines Mobilfunksystems bestimmt werden.
Dabei wird von folgenden Voraussetzungen ausgegangen:
- Die Kohärenzzeit des Kanals ist $T_{\rm coh} = 0.4 \ \rm ms$.
- Die maximale Pfadverzögerung sei $τ_{\rm max} = 25 \ \rm µ s$.
- Die Datenrate (Bitrate) beträgt $R_{\rm B} = 1 \ \rm Mbit/s$.
- Alle Unterträger werden $\rm 4–QAM$–moduliert.
Um eine gewisse Robustheit des Systems gegenüber zeit– und frequenzselektivem Fading zu gewährleisten, muss die folgende Ungleichung erfüllt werden:
- $$T_{\rm{G}} \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}.$$
Insgesamt soll folgendermaßen vorgegangen werden:
- Vorläufige Festlegung des Guard–Intervalls $(T_{\rm G}')$,
- Bestimmung der optimalen Kernsymboldauer $(T)$,
- entsprechende Festlegung der Stützstellenzahl der $\rm FFT$.
Danach ist eventuell eine erneute Bestimmung einiger Systemgrößen aufgrund der bei den Berechnungen vorgenommenen Rundungen erforderlich.
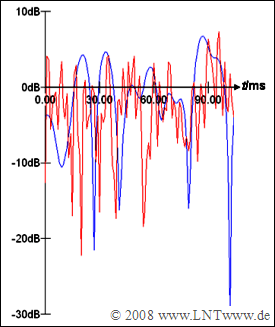
Die Grafik zeigt zwei beispielhafte Dämpfungsverläufe von Mobilfunksystemen in logarithmischer Darstellung.
- Bei der blauen Kurve geschehen die zeitlichen Veränderungen relativ langsam, bei der roten Kurve viermal so schnell.
- Demzufolge weist der blaue Kanal eine viermal größere Kohärenzzeit auf als der rote Kanal.
Hinweise:
- Die Aufgabe gehört zum Kapitel OFDM für 4G–Netze.
- Bezug genommen wird insbesondere auf die Seite Bestimmung einiger OFDM-Parameter.
- Weitere Informationen zum Thema finden Sie im LNTwww–Buch Mobile Kommunikation.
Fragebogen
Musterlösung
- Damit ist die untere Grenze der Ungleichung $T_{\rm{G}}' \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}'$ festgelegt.
- Aber auch die obere Grenze lässt sich nun berechnen, da die Kohärenzzeit $T_{\rm coh} = 400\ \rm µ s$ bekannt ist.
(2) Zur sinnvollen Lösung der Ungleichung aus (1) wird das geometrische Mittel verwendet:
- $$T_{{\rm{opt}}} = \sqrt {T_{\rm{G}} ' \cdot (T_{{\rm{coh}}} - T_{\rm{G}} ')} = \sqrt {{25\,\,{\rm µ s}} \cdot ({400\,\,{\rm µ s}} - {25\,\,{\rm µ s}})} \hspace{0.15cm}\underline { \approx {97\,\,{\rm µ s}}}.$$
(3) Die benötigte Anzahl der Nutzträger ergibt sich aus folgender Gleichung:
- $$N_{{\rm{Nutz}}} = \left\lceil {\frac{{R_{{\rm{B}}} \cdot (T + T_{\rm{G}} ')}} {{{\rm{log}_2}(M)}}}\right\rceil = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm µ s}} + {25\,\,{\rm µ s}} )} {{{\rm{log}_2}(4)}}}\right\rceil\hspace{0.15cm}\underline {= 61}.$$
(4) Die Stützstellenzahl der $\rm FFT$ muss stets eine Zweier–Potenz sein. Daraus folgt:
- $$ N_{{\rm{FFT}}} = 2^{\left\lceil {{\rm{log_2}} \hspace{0.05cm}(61 )} \right\rceil } = 2^6\hspace{0.15cm}\underline {= 64}.$$
- Ungenutzte Träger können an den Rändern des Spektrums als Guard–Band verwendet werden.
(5) Wir bezeichnen die gerundete Anzahl der Stützstellen des Guardintervalls mit $N_{\rm{G}}$. Dann gilt:
- $$N_{\rm{G}} = \left\lceil {\frac{{T_{\rm{G}} '}} {{T_{{\rm{opt}}} }} \cdot N_{{\rm{FFT}}} } \right\rceil = \left\lceil {\frac{25\,\,{\rm µ s}} {97\,\,{\rm µ s}} \cdot 64 } \right\rceil \hspace{0.15cm}\underline {= 17},$$
- $$ T_{\rm{G}} = N_{\rm{G}} \cdot \frac{{T_{{\rm{opt}}} }} {{N_{{\rm{FFT}}} }}= 17 \cdot \frac{{97\,\,{\rm µ s}}} {64}\hspace{0.15cm}\underline { \approx {26\,\,{\rm µ s}}}.$$
(6) Die Rahmendauer ergibt sich zu
- $$T_{\rm{R}} = T + T_{\rm{G}} = {97\,\,{\rm µ s}} + {26\,\,{\rm µ s}}\hspace{0.15cm}\underline {= {123\,\,{\rm µ s}}}.$$
(7) Mit den Ergebnissen der Teilaufgaben (4) und (5) erhält man:
- $$ N_{\rm{gesamt}} = N_{\rm{FFT}} + N_{\rm{G}} = 64 + 17 \hspace{0.15cm}\underline {= 81}.$$
(8) Die Neuberechnung ist nötig, da sich die Dauer des Guard–Intervalls geändert haben kann.
- Gegenüber der Teilaufgab e (3) wird die vorläufige Länge $T_{\rm{G}} '$ durch $T_{\rm{G}} $ ersetzt und man erhält ein geringfügig anderes Ergebnis:
- $$N_{\rm Nutz}' = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm µ s}} + {26\,\,{\rm µ s}} )} {{{\rm{log_2}}(4)}}}\right\rceil = \left\lceil 61.5\right\rceil\hspace{0.15cm}\underline {= 62}.$$
- Damit ergibt sich aber weiterhin $N_{\rm FFT} = 64$.