Aufgaben:Aufgabe 3.7: Bitfehlerquote (BER): Unterschied zwischen den Versionen
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
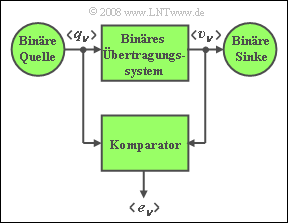
Wir betrachten ein binäres Übertragungssystem mit | Wir betrachten ein binäres Übertragungssystem mit | ||
| − | *der Quellensymbolfolge $\langle q_\nu \rangle $ und | + | *der Quellensymbolfolge $\langle q_\nu \rangle $ und |
| − | *der Sinkensymbolfolge $\langle v_\nu \rangle $. | + | *der Sinkensymbolfolge $\langle v_\nu \rangle $. |
| − | Stimmen Sinkensymbol $v_\nu$ und Quellensymbol $q_\nu$ nicht überein, so liegt ein Bitfehler vor ⇒ $e_\nu = 1$. Ansonsten gilt $e_\nu = 0$. | + | Stimmen Sinkensymbol $v_\nu$ und Quellensymbol $q_\nu$ nicht überein, so liegt ein Bitfehler vor ⇒ $e_\nu = 1$. <br>Ansonsten gilt $e_\nu = 0$. |
| − | + | $\rm (A)$ Ein wichtiges Beurteilungskriterium ist die '''Bitfehlerwahrscheinlichkeit''' (englisch: "Bit Error Probability"). | |
| − | *Mit dem Erwartungswert ${\rm E}\big[\text{ ...} \big]$ ist diese ist wie folgt definiert: | + | :*Mit dem Erwartungswert ${\rm E}\big[\text{ ...} \big]$ ist diese ist wie folgt definiert: |
| − | :$$\it p_{\rm B} = \rm E\big[\rm Pr(\it v_{\nu} \ne q_{\nu} \rm )\big]=\rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]=\lim_{{\it N}\to\infty}\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N}\rm Pr(\it e_{\nu}=\rm 1).$$ | + | ::$$\it p_{\rm B} = \rm E\big[\rm Pr(\it v_{\nu} \ne q_{\nu} \rm )\big]=\rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]=\lim_{{\it N}\to\infty}\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N}\rm Pr(\it e_{\nu}=\rm 1).$$ |
| − | *Der rechte Teil dieser Gleichung beschreibt eine Zeitmittelung | + | :*Der rechte Teil dieser Gleichung beschreibt eine Zeitmittelung; diese muss zum Beispiel bei zeitvarianten Kanälen stets angewandt werden. |
| − | *Ist die Fehlerwahrscheinlichkeit für alle Symbole gleich (was hier vorausgesetzt wird), so kann man die obige Gleichung vereinfachen: | + | :*Ist die Fehlerwahrscheinlichkeit für alle Symbole gleich (was hier vorausgesetzt wird), so kann man die obige Gleichung vereinfachen: |
| − | :$$\it p_{\rm B} = \rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]=\rm E\big[\it e_{\nu} \rm \big].$$ | + | ::$$\it p_{\rm B} = \rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]=\rm E\big[\it e_{\nu} \rm \big].$$ |
| + | :*Die Bitfehlerwahrscheinlichkeit ist eine "A-priori-Kenngröße", erlaubt also eine Vorhersage für das zu erwartende Resultat. | ||
| − | |||
| − | + | $\rm (B)$ Zur messtechnischen Ermittlung/Systemsimulation der Übertragungsqualität muss auf die '''Bitfehlerquote''' (englisch: "Bit Error Rate") übergegangen werden: | |
| − | :$$h_{\rm B}=\frac{n_{\rm B}}{N}=\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N} e_{\nu}.$$ | + | :*Die Bitfehlerquote ist eine A-posteriori-Kenngröße, die aus einem durchgeführten statistischem Experiment als [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Definition_der_Bitfehlerquote|relative Häufigkeit]] abgeleitet wird: |
| + | ::$$h_{\rm B}=\frac{n_{\rm B}}{N}=\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N} e_{\nu}.$$ | ||
| + | :* $n_{\rm B}$ gibt die Anzahl der aufgetretenen im Experiment Bitfehler an, wenn insgesamt $N$ Binärsymbole übertragen wurden. | ||
| + | :*Im Grenzfall $N \to \infty$ stimmt die relative Häufigkeit $h_{\rm B}$ mit der Wahrscheinlichkeit $p_{\rm B}$ überein. Hier soll nun die Frage geklärt werden, mit welcher statistischen Unsicherheit bei endlichem $N$ gerechnet werden muss. | ||
| − | |||
| − | |||
| − | |||
| Zeile 36: | Zeile 36: | ||
| − | + | Hinweise: | |
| − | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße|Gaußverteilte Zufallsgrößen]]. | |
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße|Gaußverteilte Zufallsgrößen]]. | + | *Lösen Sie die Aufgaben so weit wie möglich allgemein. Verwenden Sie zur Kontrolleingabe die Parameterwerte $p_{\rm B} = 10^{-3}$ und $N = 10^{5}$. |
| − | |||
| − | *Lösen Sie die Aufgaben so weit wie möglich allgemein. | ||
| − | |||
*Nachfolgend finden Sie einige Werte der sogenannten Q-Funktion: | *Nachfolgend finden Sie einige Werte der sogenannten Q-Funktion: | ||
:$$\rm Q(\rm 1.00)=\rm 0.159,\hspace{0.5cm}\rm Q(\rm 1.65)=\rm 0.050,\hspace{0.5cm}\rm Q(\rm 1.96)=\rm 0.025,\hspace{0.5cm}\rm Q(\rm 2.59)=\rm 0.005.$$ | :$$\rm Q(\rm 1.00)=\rm 0.159,\hspace{0.5cm}\rm Q(\rm 1.65)=\rm 0.050,\hspace{0.5cm}\rm Q(\rm 1.96)=\rm 0.025,\hspace{0.5cm}\rm Q(\rm 2.59)=\rm 0.005.$$ | ||
| Zeile 54: | Zeile 51: | ||
{Welche der folgenden Aussagen sind zutreffend? | {Welche der folgenden Aussagen sind zutreffend? | ||
|type="[]"} | |type="[]"} | ||
| − | - Für $n_{\rm B}$ sind alle Werte $(0$, ... , $N)$ gleichwahrscheinlich. | + | - Für $n_{\rm B}$ sind alle Werte $(0$, ... , $N)$ gleichwahrscheinlich. |
| − | + Die Zufallsgröße $n_{\rm B}$ ist binomialverteilt. | + | + Die Zufallsgröße $n_{\rm B}$ ist binomialverteilt. |
| − | + Mit $p_{\rm B} = 10^{-3}$ und $N = 10^{5}$ ergibt sich ${\rm E}\big[n_{\rm B}\big] = 100$. | + | + Mit $p_{\rm B} = 10^{-3}$ und $N = 10^{5}$ ergibt sich ${\rm E}\big[n_{\rm B}\big] = 100$. |
| − | {Wie groß ist die Streuung der Zufallsgröße $n_{\rm B}$ für $p_{\rm B} = 10^{-3}$ und $N = 10^{5}$? | + | {Wie groß ist die Streuung der Zufallsgröße $n_{\rm B}$ für $p_{\rm B} = 10^{-3}$ und $N = 10^{5}$? |
|type="{}"} | |type="{}"} | ||
$\sigma_{n{\rm B}} \ = \ $ { 10 3% } | $\sigma_{n{\rm B}} \ = \ $ { 10 3% } | ||
| − | {Welche Werte kann die Bitfehlerquote $h_{\rm B}$ annehmen? Zeigen Sie, dass der lineare Mittelwert $m_{h{\rm B}}$ dieser Zufallsgröße gleich der tatsächlichen Bitfehlerwahrscheinlichkeit $p_{\rm B}$ ist. Wie groß ist deren Streuung? | + | {Welche Werte kann die Bitfehlerquote $h_{\rm B}$ annehmen? <br>Zeigen Sie, dass der lineare Mittelwert $m_{h{\rm B}}$ dieser Zufallsgröße gleich der tatsächlichen Bitfehlerwahrscheinlichkeit $p_{\rm B}$ ist. Wie groß ist deren Streuung? |
|type="{}"} | |type="{}"} | ||
$\sigma_{h{\rm B}} \ = \ $ { 0.0001 3% } | $\sigma_{h{\rm B}} \ = \ $ { 0.0001 3% } | ||
| − | {Unter gewissen Voraussetzungen kann eine binomialverteilte Zufallsgröße durch eine Gaußverteilung mit gleichem Mittelwert $(m_{h{\rm B}})$ und gleicher Streuung $(\sigma_{h{\rm B}})$ angenähert werden. Welche Aussage ist zutreffend? | + | {Unter gewissen Voraussetzungen kann eine binomialverteilte Zufallsgröße durch eine Gaußverteilung mit gleichem Mittelwert $(m_{h{\rm B}})$ und gleicher Streuung $(\sigma_{h{\rm B}})$ angenähert werden. Welche Aussage ist zutreffend? |
|type="()"} | |type="()"} | ||
| − | + ${\rm Pr}(|h_{\rm B} - p_{\rm B}| \le \varepsilon)=1- 2\cdot \rm Q({\varepsilon}/{\sigma_{h{\rm B}}}).$ | + | + ${\rm Pr}(\hspace{0.05cm}|\hspace{0.05cm}h_{\rm B} - p_{\rm B}\hspace{0.05cm}| \le \varepsilon)=1- 2\cdot \rm Q({\varepsilon}/{\sigma_{{\it h}{\rm B}}}).$ |
| − | - ${\rm Pr}(|h_{\rm B} - p_{\rm B}| \le \varepsilon)=1- \rm Q({\varepsilon}/{2\cdot \sigma_{h{\rm B}}}).$ | + | - ${\rm Pr}(\hspace{0.05cm}|\hspace{0.05cm}h_{\rm B} - p_{\rm B}\hspace{0.05cm}| \le \varepsilon)=1- \rm Q({\varepsilon}/{2\cdot \sigma_{{\it h}{\rm B}}}).$ |
| − | {Zur Abkürzung verwenden wir das Konfidenzniveau $p_\varepsilon = {\rm Pr}(|h_{\rm B} - p_{\rm B}| \le \varepsilon)$. | + | {Zur Abkürzung verwenden wir das Konfidenzniveau $p_\varepsilon = {\rm Pr}(\hspace{0.05cm}|\hspace{0.05cm}h_{\rm B} - p_{\rm B}\hspace{0.05cm}| \le \varepsilon)$. Welches $p_\varepsilon$ ergibt sich mit $\varepsilon = 10^{-4}$, $p_{\rm B} = 10^{-3}$ und $N = 10^{5}$ ? |
|type="{}"} | |type="{}"} | ||
$p_\varepsilon \ = \ $ { 0.684 3% } | $p_\varepsilon \ = \ $ { 0.684 3% } | ||
| − | {Das Argument der Q-Funktion sei $\alpha$. Wie groß muss $\alpha$ mindestens gewählt werden, damit das Konfidenzniveau $p_\varepsilon = 95\%$ beträgt? | + | {Das Argument der Q-Funktion sei $\alpha$. Wie groß muss $\alpha$ mindestens gewählt werden, damit das Konfidenzniveau $p_\varepsilon = 95\%$ beträgt ? |
|type="{}"} | |type="{}"} | ||
$\alpha_{\rm min} \ = \ $ { 1.96 3% } | $\alpha_{\rm min} \ = \ $ { 1.96 3% } | ||
| − | {Es gelte weiterhin $p_{\rm B} = 10^{-3}$ und $p_\varepsilon = 95\%$ Über wie viele Symbole muss | + | {Es gelte weiterhin $p_{\rm B} = 10^{-3}$ und $p_\varepsilon = 95\%$. Über wie viele Symbole $(N_\text{min})$ muss mindestens gemittelt werden, <br>damit die ermittelte Bitfehlerquote im Bereich zwischen $0.9 \cdot 10^{-3}$ und $1.1 \cdot 10^{-3}$ liegt $(\varepsilon = 10^{-4}, \ \text{10% vom Sollwert)}$ ? |
|type="{}"} | |type="{}"} | ||
$N_\text{min} \ = \ ${ 400000 3% } | $N_\text{min} \ = \ ${ 400000 3% } | ||
| Zeile 96: | Zeile 93: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die <u>beiden letzten Aussagen</u> stimmen: | + | '''(1)''' Die <u>beiden letzten Aussagen</u> stimmen: |
| − | *Bezüglich der Zufallsgröße $n_{\rm B}$ liegt der klassische Fall einer Binomialverteilung vor. | + | *Bezüglich der Zufallsgröße $n_{\rm B}$ liegt der klassische Fall einer Binomialverteilung vor. |
| − | *Es wird die Summe über $N$ binäre Zufallsgrößen gebildet. | + | *Es wird die Summe über $N$ binäre Zufallsgrößen gebildet. Die möglichen Werte von $n_{\rm B}$ liegen somit zwischen $0$ und $N$. |
| − | |||
*Der lineare Mittelwert ergibt $m_{n{\rm B}}=p_{\rm B}\cdot N=\rm 10^{-3}\cdot 10^{5}=\rm 100.$ | *Der lineare Mittelwert ergibt $m_{n{\rm B}}=p_{\rm B}\cdot N=\rm 10^{-3}\cdot 10^{5}=\rm 100.$ | ||
| + | |||
| Zeile 108: | Zeile 105: | ||
| − | |||
| − | Für den Mittelwert erhält man: | + | '''(3)''' Mögliche Werte von $h_{\rm B}$ sind alle ganzzahligen Vielfachen von $1/N$. Diese liegen alle zwischen $0$ und $1$. |
| + | |||
| + | *Für den Mittelwert erhält man: | ||
:$$m_{h{\rm B}}=m_{n{\rm B}}/N=p_{\rm B} = 10^{-3}.$$ | :$$m_{h{\rm B}}=m_{n{\rm B}}/N=p_{\rm B} = 10^{-3}.$$ | ||
| + | *Die Streuung ergibt sich zu | ||
| + | :$$\sigma_{h{\rm B}}=\frac{\sigma_{n{\rm B}}}{N}=\sqrt{\frac{ p_{\rm B}\cdot (\rm 1- \it p_{\rm B}{\rm )}}{N}}\hspace{0.15cm}\underline{\approx \rm 0.0001}.$$ | ||
| − | |||
| − | |||
| + | '''(4)''' Richtig ist <u>der erste Vorschlag</u>. Es gilt: | ||
| + | :$${\rm Pr}(h_{\rm B} > p_{\rm B} + \varepsilon)=\rm Q({\it\varepsilon}/{\it\sigma_{h{\rm B}}}),$$ | ||
| + | :$$\rm Pr(\it h_{\rm B} < p_{\rm B} - \varepsilon {\rm )}=\rm Q(\it{\varepsilon}/{\sigma_{h{\rm B}}}{\rm )}$$ | ||
| + | :$$\Rightarrow \hspace{0.5cm}\rm Pr(\it |h_{\rm B} - p_{\rm B}| \le \varepsilon \rm )=\rm 1-\rm 2\cdot \rm Q({\it \varepsilon}/{\it \sigma_{h{\rm B}}}).$$ | ||
| − | |||
| − | |||
| − | '''(5)''' Man erhält mit den Zahlenwerten $\varepsilon = \sigma_{h{\rm B}} = 10^{-4}$: | + | '''(5)''' Man erhält mit den Zahlenwerten $\varepsilon = \sigma_{h{\rm B}} = 10^{-4}$: |
:$$p_{\varepsilon}=\rm 1-\rm 2\cdot \rm Q(\frac{\rm 10^{\rm -4}}{\rm 10^{\rm -4}} {\rm )}=\rm 1-\rm 2\cdot\rm Q(\rm 1)\hspace{0.15cm}\underline{\approx\rm 0.684}.$$ | :$$p_{\varepsilon}=\rm 1-\rm 2\cdot \rm Q(\frac{\rm 10^{\rm -4}}{\rm 10^{\rm -4}} {\rm )}=\rm 1-\rm 2\cdot\rm Q(\rm 1)\hspace{0.15cm}\underline{\approx\rm 0.684}.$$ | ||
| − | + | In Worten: Bestimmt man die Bitfehlerquote per Simulation über $10^5$ Symbole, so erhält man mit einem Konfidenzniveau von $\underline{68.4\%}$ einen Wert zwischen $0.9 \cdot 10^{-3}$ und $1.1 \cdot 10^{-3}$, wenn $p_{\rm B} = 10^{-3}$ ist. | |
| − | '''(6)''' Aus der Beziehung $p_{\varepsilon}=\rm 1-\rm 2\cdot {\rm Q}(\alpha) = 0.95$ folgt direkt: | + | |
| + | '''(6)''' Aus der Beziehung $p_{\varepsilon}=\rm 1-\rm 2\cdot {\rm Q}(\alpha) = 0.95$ folgt direkt: | ||
:$$\alpha_{\rm min}=\rm Q^{\rm -1}\Big(\frac{\rm 1-\it p_{\varepsilon}}{\rm 2}\Big)=\rm Q^{\rm -1}(\rm 0.025)\hspace{0.15cm}\underline{=\rm 1.96}\hspace{0.15cm}{\approx\rm 2}.$$ | :$$\alpha_{\rm min}=\rm Q^{\rm -1}\Big(\frac{\rm 1-\it p_{\varepsilon}}{\rm 2}\Big)=\rm Q^{\rm -1}(\rm 0.025)\hspace{0.15cm}\underline{=\rm 1.96}\hspace{0.15cm}{\approx\rm 2}.$$ | ||
| − | '''(7)''' Es muss $\alpha = \varepsilon/\sigma_{h{\rm B}}$ gelten. Mit dem Ergebnis der Teilaufgabe '''(2)''' folgt dann: | + | |
| + | '''(7)''' Es muss $\alpha = \varepsilon/\sigma_{h{\rm B}}$ gelten. Mit dem Ergebnis der Teilaufgabe '''(2)''' folgt dann: | ||
:$$\frac{\varepsilon}{\sqrt{p_{\rm B}\cdot(\rm 1-\it p_{\rm B})/N}}\ge {\rm 2} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} | :$$\frac{\varepsilon}{\sqrt{p_{\rm B}\cdot(\rm 1-\it p_{\rm B})/N}}\ge {\rm 2} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} | ||
| − | N\ge \frac{\rm 4\cdot \it p_{\rm B}\cdot(\rm 1-\it p_{\rm B})}{\varepsilon^{\rm 2}}\approx \frac{\rm 4\cdot 10^{-3}}{10^{-8}}\hspace{0.15cm}\underline{=\rm | + | N\ge \frac{\rm 4\cdot \it p_{\rm B}\cdot(\rm 1-\it p_{\rm B})}{\varepsilon^{\rm 2}}\approx \frac{\rm 4\cdot 10^{-3}}{10^{-8}}\hspace{0.15cm}\underline{=\rm 400\hspace{0.08cm}000}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 2. Februar 2022, 12:20 Uhr
Wir betrachten ein binäres Übertragungssystem mit
- der Quellensymbolfolge $\langle q_\nu \rangle $ und
- der Sinkensymbolfolge $\langle v_\nu \rangle $.
Stimmen Sinkensymbol $v_\nu$ und Quellensymbol $q_\nu$ nicht überein, so liegt ein Bitfehler vor ⇒ $e_\nu = 1$.
Ansonsten gilt $e_\nu = 0$.
$\rm (A)$ Ein wichtiges Beurteilungskriterium ist die Bitfehlerwahrscheinlichkeit (englisch: "Bit Error Probability").
- Mit dem Erwartungswert ${\rm E}\big[\text{ ...} \big]$ ist diese ist wie folgt definiert:
- $$\it p_{\rm B} = \rm E\big[\rm Pr(\it v_{\nu} \ne q_{\nu} \rm )\big]=\rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]=\lim_{{\it N}\to\infty}\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N}\rm Pr(\it e_{\nu}=\rm 1).$$
- Der rechte Teil dieser Gleichung beschreibt eine Zeitmittelung; diese muss zum Beispiel bei zeitvarianten Kanälen stets angewandt werden.
- Ist die Fehlerwahrscheinlichkeit für alle Symbole gleich (was hier vorausgesetzt wird), so kann man die obige Gleichung vereinfachen:
- $$\it p_{\rm B} = \rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]=\rm E\big[\it e_{\nu} \rm \big].$$
- Die Bitfehlerwahrscheinlichkeit ist eine "A-priori-Kenngröße", erlaubt also eine Vorhersage für das zu erwartende Resultat.
$\rm (B)$ Zur messtechnischen Ermittlung/Systemsimulation der Übertragungsqualität muss auf die Bitfehlerquote (englisch: "Bit Error Rate") übergegangen werden:
- Die Bitfehlerquote ist eine A-posteriori-Kenngröße, die aus einem durchgeführten statistischem Experiment als relative Häufigkeit abgeleitet wird:
- $$h_{\rm B}=\frac{n_{\rm B}}{N}=\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N} e_{\nu}.$$
- $n_{\rm B}$ gibt die Anzahl der aufgetretenen im Experiment Bitfehler an, wenn insgesamt $N$ Binärsymbole übertragen wurden.
- Im Grenzfall $N \to \infty$ stimmt die relative Häufigkeit $h_{\rm B}$ mit der Wahrscheinlichkeit $p_{\rm B}$ überein. Hier soll nun die Frage geklärt werden, mit welcher statistischen Unsicherheit bei endlichem $N$ gerechnet werden muss.
Hinweise:
- Die Aufgabe gehört zum Kapitel Gaußverteilte Zufallsgrößen.
- Lösen Sie die Aufgaben so weit wie möglich allgemein. Verwenden Sie zur Kontrolleingabe die Parameterwerte $p_{\rm B} = 10^{-3}$ und $N = 10^{5}$.
- Nachfolgend finden Sie einige Werte der sogenannten Q-Funktion:
- $$\rm Q(\rm 1.00)=\rm 0.159,\hspace{0.5cm}\rm Q(\rm 1.65)=\rm 0.050,\hspace{0.5cm}\rm Q(\rm 1.96)=\rm 0.025,\hspace{0.5cm}\rm Q(\rm 2.59)=\rm 0.005.$$
Fragebogen
Musterlösung
- Bezüglich der Zufallsgröße $n_{\rm B}$ liegt der klassische Fall einer Binomialverteilung vor.
- Es wird die Summe über $N$ binäre Zufallsgrößen gebildet. Die möglichen Werte von $n_{\rm B}$ liegen somit zwischen $0$ und $N$.
- Der lineare Mittelwert ergibt $m_{n{\rm B}}=p_{\rm B}\cdot N=\rm 10^{-3}\cdot 10^{5}=\rm 100.$
(2) Für die Streuung der Binomialverteilung gilt mit guter Näherung:
- $$\sigma_{n{\rm B}}=\sqrt{N\cdot p_{\rm B}\cdot (\rm 1- \it p_{\rm B}{\rm )}} \hspace{0.15cm}\underline{\approx 10}.$$
(3) Mögliche Werte von $h_{\rm B}$ sind alle ganzzahligen Vielfachen von $1/N$. Diese liegen alle zwischen $0$ und $1$.
- Für den Mittelwert erhält man:
- $$m_{h{\rm B}}=m_{n{\rm B}}/N=p_{\rm B} = 10^{-3}.$$
- Die Streuung ergibt sich zu
- $$\sigma_{h{\rm B}}=\frac{\sigma_{n{\rm B}}}{N}=\sqrt{\frac{ p_{\rm B}\cdot (\rm 1- \it p_{\rm B}{\rm )}}{N}}\hspace{0.15cm}\underline{\approx \rm 0.0001}.$$
(4) Richtig ist der erste Vorschlag. Es gilt:
- $${\rm Pr}(h_{\rm B} > p_{\rm B} + \varepsilon)=\rm Q({\it\varepsilon}/{\it\sigma_{h{\rm B}}}),$$
- $$\rm Pr(\it h_{\rm B} < p_{\rm B} - \varepsilon {\rm )}=\rm Q(\it{\varepsilon}/{\sigma_{h{\rm B}}}{\rm )}$$
- $$\Rightarrow \hspace{0.5cm}\rm Pr(\it |h_{\rm B} - p_{\rm B}| \le \varepsilon \rm )=\rm 1-\rm 2\cdot \rm Q({\it \varepsilon}/{\it \sigma_{h{\rm B}}}).$$
(5) Man erhält mit den Zahlenwerten $\varepsilon = \sigma_{h{\rm B}} = 10^{-4}$:
- $$p_{\varepsilon}=\rm 1-\rm 2\cdot \rm Q(\frac{\rm 10^{\rm -4}}{\rm 10^{\rm -4}} {\rm )}=\rm 1-\rm 2\cdot\rm Q(\rm 1)\hspace{0.15cm}\underline{\approx\rm 0.684}.$$
In Worten: Bestimmt man die Bitfehlerquote per Simulation über $10^5$ Symbole, so erhält man mit einem Konfidenzniveau von $\underline{68.4\%}$ einen Wert zwischen $0.9 \cdot 10^{-3}$ und $1.1 \cdot 10^{-3}$, wenn $p_{\rm B} = 10^{-3}$ ist.
(6) Aus der Beziehung $p_{\varepsilon}=\rm 1-\rm 2\cdot {\rm Q}(\alpha) = 0.95$ folgt direkt:
- $$\alpha_{\rm min}=\rm Q^{\rm -1}\Big(\frac{\rm 1-\it p_{\varepsilon}}{\rm 2}\Big)=\rm Q^{\rm -1}(\rm 0.025)\hspace{0.15cm}\underline{=\rm 1.96}\hspace{0.15cm}{\approx\rm 2}.$$
(7) Es muss $\alpha = \varepsilon/\sigma_{h{\rm B}}$ gelten. Mit dem Ergebnis der Teilaufgabe (2) folgt dann:
- $$\frac{\varepsilon}{\sqrt{p_{\rm B}\cdot(\rm 1-\it p_{\rm B})/N}}\ge {\rm 2} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} N\ge \frac{\rm 4\cdot \it p_{\rm B}\cdot(\rm 1-\it p_{\rm B})}{\varepsilon^{\rm 2}}\approx \frac{\rm 4\cdot 10^{-3}}{10^{-8}}\hspace{0.15cm}\underline{=\rm 400\hspace{0.08cm}000}.$$