Aufgaben:Aufgabe 3.10Z: Rayleigh? Oder Rice?: Unterschied zwischen den Versionen
Aus LNTwww
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
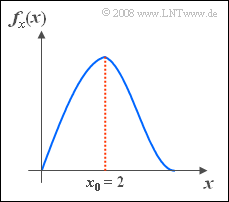
| − | [[Datei:P_ID149__Sto_Z_3_10.png|right|frame|Beschreibt die vorliegende WDF Rayleigh oder Rice?]] | + | [[Datei:P_ID149__Sto_Z_3_10.png|right|frame|Beschreibt die vorliegende WDF "Rayleigh" oder "Rice"?]] |
| − | Die Wahrscheinlichkeitsdichtefunktion der Zufallsgröße $x$ ist wie folgt gegeben: | + | Die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ der Zufallsgröße $x$ ist wie folgt gegeben: |
:$$f_x(x)=\frac{\it x}{\lambda^{2}}\cdot{\rm e}^{-x^{\rm 2}/(\lambda^{\rm 2})}.$$ | :$$f_x(x)=\frac{\it x}{\lambda^{2}}\cdot{\rm e}^{-x^{\rm 2}/(\lambda^{\rm 2})}.$$ | ||
| − | Entsprechend gilt für die zugehörige Verteilungsfunktion: | + | Entsprechend gilt für die zugehörige Verteilungsfunktion $\rm (VTF)$: |
:$$F_x(r)= {\rm Pr}(x \le r) = 1-{\rm e}^{- r^{\rm 2}/(2 \lambda^{\rm 2})}.$$ | :$$F_x(r)= {\rm Pr}(x \le r) = 1-{\rm e}^{- r^{\rm 2}/(2 \lambda^{\rm 2})}.$$ | ||
| − | *Bekannt ist, dass der Wert $x_0 = 2$ am häufigsten auftritt. | + | *Bekannt ist, dass der Wert $x_0 = 2$ am häufigsten auftritt. |
| − | *Das bedeutet auch, dass die WDF $f_x(x)$ bei $x = x_0 $ maximal ist. | + | *Das bedeutet auch, dass die WDF $f_x(x)$ bei $x = x_0 $ maximal ist. |
| − | + | Hinweise: | |
| − | |||
| − | |||
| − | |||
*Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Weitere_Verteilungen|Weitere Verteilungen]]. | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Weitere_Verteilungen|Weitere Verteilungen]]. | ||
| − | *Insbesondere wird auf die Seiten [[Stochastische_Signaltheorie/Weitere_Verteilungen#Rayleighverteilung|Rayleighverteilung]] und [[Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung|Riceverteilung]] Bezug genommen . | + | *Insbesondere wird auf die Seiten [[Stochastische_Signaltheorie/Weitere_Verteilungen#Rayleighverteilung|"Rayleighverteilung"]] und [[Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung|"Riceverteilung"]] Bezug genommen. |
| − | *Sie können Ihre Ergebnisse mit interaktiven Applet [[Applets:WDF,_VTF_und_Momente_spezieller_Verteilungen_(Applet)|WDF, VTF und Momente spezieller Verteilungen]] überprüfen. | + | *Sie können Ihre Ergebnisse mit interaktiven Applet [[Applets:WDF,_VTF_und_Momente_spezieller_Verteilungen_(Applet)|"WDF, VTF und Momente spezieller Verteilungen"]] überprüfen. |
*Berücksichtigen Sie bei der Lösung das folgende bestimmte Integral: | *Berücksichtigen Sie bei der Lösung das folgende bestimmte Integral: | ||
:$$\int_{0}^{\infty}x^{\rm 2}\cdot {\rm e}^{ -x^{\rm 2}/\rm 2} \, {\rm d}x=\sqrt{{\pi}/{\rm 2}}.$$ | :$$\int_{0}^{\infty}x^{\rm 2}\cdot {\rm e}^{ -x^{\rm 2}/\rm 2} \, {\rm d}x=\sqrt{{\pi}/{\rm 2}}.$$ | ||
| Zeile 46: | Zeile 43: | ||
| − | {Wie groß ist die Wahrscheinlichkeit, dass $x$ kleiner als $x_0 = 2$ ist? | + | {Wie groß ist die Wahrscheinlichkeit, dass $x$ kleiner als $x_0 = 2$ ist? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(x < x_0 ) \ = \ $ { 39.3 3% } $\ \%$ | ${\rm Pr}(x < x_0 ) \ = \ $ { 39.3 3% } $\ \%$ | ||
| − | {Wie groß ist der Mittelwert der Zufallsgröße $x$? Interpretation. | + | {Wie groß ist der Mittelwert der Zufallsgröße $x$? Interpretation. |
|type="{}"} | |type="{}"} | ||
$m_x \ = \ $ { 2.506 3% } | $m_x \ = \ $ { 2.506 3% } | ||
| Zeile 66: | Zeile 63: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig ist <u>allein der zweite Lösungsvorschlag</u>. | + | '''(1)''' Richtig ist <u>allein der zweite Lösungsvorschlag</u>. |
| − | *Aufgrund der gegebenen WDF liegt keine Riceverteilung, sondern eine Rayleighverteilung vor. | + | *Aufgrund der gegebenen WDF liegt keine Riceverteilung, sondern eine <u>Rayleighverteilung</u> vor. |
| − | *Diese ist um den Mittelwert $m_x$ unsymmetrisch, so dass $\mu_3 \ne 0$ ist. | + | *Diese ist um den Mittelwert $m_x$ unsymmetrisch, so dass $\mu_3 \ne 0$ ist. |
| − | *Nur bei einer gaußverteilten Zufallsgröße gilt für die Kurtosis $K = 3$. | + | *Nur bei einer gaußverteilten Zufallsgröße gilt für die Kurtosis $K = 3$. |
| − | *Bei der Rayleighverteilung ergibt sich aufgrund ausgeprägterer WDF–Ausläufer ein größerer Wert $(K = 3.245)$, und zwar unabhängig von $\lambda$. | + | *Bei der Rayleighverteilung ergibt sich aufgrund ausgeprägterer WDF–Ausläufer ein größerer Wert $(K = 3.245)$, und zwar unabhängig von $\lambda$. |
| − | '''(2)''' Die Ableitung der WDF nach $x$ liefert: | + | |
| + | '''(2)''' Die Ableitung der WDF nach $x$ liefert: | ||
:$$\frac{{\rm d} f_x(x)}{{\rm d} x} = \frac{\rm 1}{\lambda^{\rm 2}}\cdot{\rm e}^{ -{x^{\rm 2}}/({2 \lambda^{\rm 2}})}+\frac{ x}{ \lambda^{\rm 2}}\cdot{\rm e}^{ -{x^{\rm 2}}/({ 2 \lambda^{\rm 2}})}\cdot(-\frac{2 x}{2 \lambda^{\rm 2}}).$$ | :$$\frac{{\rm d} f_x(x)}{{\rm d} x} = \frac{\rm 1}{\lambda^{\rm 2}}\cdot{\rm e}^{ -{x^{\rm 2}}/({2 \lambda^{\rm 2}})}+\frac{ x}{ \lambda^{\rm 2}}\cdot{\rm e}^{ -{x^{\rm 2}}/({ 2 \lambda^{\rm 2}})}\cdot(-\frac{2 x}{2 \lambda^{\rm 2}}).$$ | ||
| − | Daraus folgt als Bestimmungsgleichung für $x_0$ (nur die positive Lösung ist sinnvoll): | + | *Daraus folgt als Bestimmungsgleichung für $x_0$ (nur die positive Lösung ist sinnvoll): |
:$$\frac{1}{\lambda^{\rm 2}}\cdot{\rm e}^{ -{x_{\rm 0}^{\rm 2}}/{(2 \lambda^{\rm 2}})}\cdot(\rm 1-{\it x_{\rm 0}^{\rm 2}}/{\it \lambda^{\rm 2}})=0 \quad \Rightarrow \quad {\it x}_0=\it \lambda.$$ | :$$\frac{1}{\lambda^{\rm 2}}\cdot{\rm e}^{ -{x_{\rm 0}^{\rm 2}}/{(2 \lambda^{\rm 2}})}\cdot(\rm 1-{\it x_{\rm 0}^{\rm 2}}/{\it \lambda^{\rm 2}})=0 \quad \Rightarrow \quad {\it x}_0=\it \lambda.$$ | ||
| − | Somit erhält man für den Verteilungsparameter $\lambda = x_0\hspace{0.15cm}\underline{= 2}$. | + | *Somit erhält man für den Verteilungsparameter $\lambda = x_0\hspace{0.15cm}\underline{= 2}$. |
| − | '''(3)''' Die gesuchte Wahrscheinlichkeit ist gleich der Verteilungsfunktion an der Stelle $r = x_0 = \lambda$: | + | |
| + | '''(3)''' Die gesuchte Wahrscheinlichkeit ist gleich der Verteilungsfunktion an der Stelle $r = x_0 = \lambda$: | ||
:$${\rm Pr}(x<x_{\rm 0})={\rm Pr}( x \le x_{\rm 0})= | :$${\rm Pr}(x<x_{\rm 0})={\rm Pr}( x \le x_{\rm 0})= | ||
| − | F_x(x_{\rm 0})=1-{\rm e}^{-{\lambda^{\rm 2}}/({ 2 \lambda^{\rm 2}})}=1-{\rm e}^{-0.5}\hspace{0.15cm}\underline{=\rm | + | F_x(x_{\rm 0})=1-{\rm e}^{-{\lambda^{\rm 2}}/({ 2 \lambda^{\rm 2}})}=1-{\rm e}^{-0.5}\hspace{0.15cm}\underline{=\rm 39.3\%}.$$ |
| + | |||
| Zeile 90: | Zeile 90: | ||
:$$m_x=\int_{-\infty}^{+\infty}\hspace{-0.45cm}x\cdot f_x(x)\,{\rm d}x=\int_{\rm 0}^{\infty}\frac{\it x^{\rm 2}}{\it \lambda^{\rm 2}} \cdot \rm e^{-{\it x^{\rm 2}}/({\rm 2\it \lambda^{\rm 2}})}\,{\rm d}\it x = \sqrt{{\rm \pi}/{\rm 2}}\cdot \it \lambda\hspace{0.15cm}\underline{=\rm 2.506}.$$ | :$$m_x=\int_{-\infty}^{+\infty}\hspace{-0.45cm}x\cdot f_x(x)\,{\rm d}x=\int_{\rm 0}^{\infty}\frac{\it x^{\rm 2}}{\it \lambda^{\rm 2}} \cdot \rm e^{-{\it x^{\rm 2}}/({\rm 2\it \lambda^{\rm 2}})}\,{\rm d}\it x = \sqrt{{\rm \pi}/{\rm 2}}\cdot \it \lambda\hspace{0.15cm}\underline{=\rm 2.506}.$$ | ||
| − | Der Mittelwert $m_x$ ist natürlich größer als $x_0$ (= Maximalwert der WDF), da die WDF zwar nach unten, aber nicht nach oben begrenzt ist. | + | *Der Mittelwert $m_x$ ist natürlich größer als $x_0$ $(=$ Maximalwert der WDF$)$, da die WDF zwar nach unten, aber nicht nach oben begrenzt ist. |
| + | |||
| Zeile 96: | Zeile 97: | ||
:$${\rm Pr}(x>m_x)=1- F_x(m_x).$$ | :$${\rm Pr}(x>m_x)=1- F_x(m_x).$$ | ||
| − | Mit der angegebenen Verteilungsfunktion und dem Ergebnis der Teilaufgabe '''(4)''' erhält man: | + | *Mit der angegebenen Verteilungsfunktion und dem Ergebnis der Teilaufgabe '''(4)''' erhält man: |
| − | :$${\rm Pr}(x>m_x)={\rm e}^{-{m_x^{\rm 2}}/({ 2\lambda^{\rm 2})}}={\rm e}^{-\pi/ 4}\hspace{0.15cm}\underline{\approx \rm | + | :$${\rm Pr}(x>m_x)={\rm e}^{-{m_x^{\rm 2}}/({ 2\lambda^{\rm 2})}}={\rm e}^{-\pi/ 4}\hspace{0.15cm}\underline{\approx \rm 45.6\%}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 3. Februar 2022, 12:07 Uhr
Die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ der Zufallsgröße $x$ ist wie folgt gegeben:
- $$f_x(x)=\frac{\it x}{\lambda^{2}}\cdot{\rm e}^{-x^{\rm 2}/(\lambda^{\rm 2})}.$$
Entsprechend gilt für die zugehörige Verteilungsfunktion $\rm (VTF)$:
- $$F_x(r)= {\rm Pr}(x \le r) = 1-{\rm e}^{- r^{\rm 2}/(2 \lambda^{\rm 2})}.$$
- Bekannt ist, dass der Wert $x_0 = 2$ am häufigsten auftritt.
- Das bedeutet auch, dass die WDF $f_x(x)$ bei $x = x_0 $ maximal ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Verteilungen.
- Insbesondere wird auf die Seiten "Rayleighverteilung" und "Riceverteilung" Bezug genommen.
- Sie können Ihre Ergebnisse mit interaktiven Applet "WDF, VTF und Momente spezieller Verteilungen" überprüfen.
- Berücksichtigen Sie bei der Lösung das folgende bestimmte Integral:
- $$\int_{0}^{\infty}x^{\rm 2}\cdot {\rm e}^{ -x^{\rm 2}/\rm 2} \, {\rm d}x=\sqrt{{\pi}/{\rm 2}}.$$
Fragebogen
Musterlösung
(1) Richtig ist allein der zweite Lösungsvorschlag.
- Aufgrund der gegebenen WDF liegt keine Riceverteilung, sondern eine Rayleighverteilung vor.
- Diese ist um den Mittelwert $m_x$ unsymmetrisch, so dass $\mu_3 \ne 0$ ist.
- Nur bei einer gaußverteilten Zufallsgröße gilt für die Kurtosis $K = 3$.
- Bei der Rayleighverteilung ergibt sich aufgrund ausgeprägterer WDF–Ausläufer ein größerer Wert $(K = 3.245)$, und zwar unabhängig von $\lambda$.
(2) Die Ableitung der WDF nach $x$ liefert:
- $$\frac{{\rm d} f_x(x)}{{\rm d} x} = \frac{\rm 1}{\lambda^{\rm 2}}\cdot{\rm e}^{ -{x^{\rm 2}}/({2 \lambda^{\rm 2}})}+\frac{ x}{ \lambda^{\rm 2}}\cdot{\rm e}^{ -{x^{\rm 2}}/({ 2 \lambda^{\rm 2}})}\cdot(-\frac{2 x}{2 \lambda^{\rm 2}}).$$
- Daraus folgt als Bestimmungsgleichung für $x_0$ (nur die positive Lösung ist sinnvoll):
- $$\frac{1}{\lambda^{\rm 2}}\cdot{\rm e}^{ -{x_{\rm 0}^{\rm 2}}/{(2 \lambda^{\rm 2}})}\cdot(\rm 1-{\it x_{\rm 0}^{\rm 2}}/{\it \lambda^{\rm 2}})=0 \quad \Rightarrow \quad {\it x}_0=\it \lambda.$$
- Somit erhält man für den Verteilungsparameter $\lambda = x_0\hspace{0.15cm}\underline{= 2}$.
(3) Die gesuchte Wahrscheinlichkeit ist gleich der Verteilungsfunktion an der Stelle $r = x_0 = \lambda$:
- $${\rm Pr}(x<x_{\rm 0})={\rm Pr}( x \le x_{\rm 0})= F_x(x_{\rm 0})=1-{\rm e}^{-{\lambda^{\rm 2}}/({ 2 \lambda^{\rm 2}})}=1-{\rm e}^{-0.5}\hspace{0.15cm}\underline{=\rm 39.3\%}.$$
(4) Der Mittelwert kann beispielsweise nach folgender Gleichung ermittelt werden:
- $$m_x=\int_{-\infty}^{+\infty}\hspace{-0.45cm}x\cdot f_x(x)\,{\rm d}x=\int_{\rm 0}^{\infty}\frac{\it x^{\rm 2}}{\it \lambda^{\rm 2}} \cdot \rm e^{-{\it x^{\rm 2}}/({\rm 2\it \lambda^{\rm 2}})}\,{\rm d}\it x = \sqrt{{\rm \pi}/{\rm 2}}\cdot \it \lambda\hspace{0.15cm}\underline{=\rm 2.506}.$$
- Der Mittelwert $m_x$ ist natürlich größer als $x_0$ $(=$ Maximalwert der WDF$)$, da die WDF zwar nach unten, aber nicht nach oben begrenzt ist.
(5) Allgemein gilt für die gesuchte Wahrscheinlichkeit:
- $${\rm Pr}(x>m_x)=1- F_x(m_x).$$
- Mit der angegebenen Verteilungsfunktion und dem Ergebnis der Teilaufgabe (4) erhält man:
- $${\rm Pr}(x>m_x)={\rm e}^{-{m_x^{\rm 2}}/({ 2\lambda^{\rm 2})}}={\rm e}^{-\pi/ 4}\hspace{0.15cm}\underline{\approx \rm 45.6\%}.$$