Stochastische Signaltheorie/Momente einer diskreten Zufallsgröße: Unterschied zwischen den Versionen
| (19 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Berechnung als Schar- bzw. Zeitmittelwert== | ==Berechnung als Schar- bzw. Zeitmittelwert== | ||
| − | Die Wahrscheinlichkeiten | + | <br> |
| + | Die Wahrscheinlichkeiten und die relativen Häufigkeiten liefern weitreichende Informationen über eine diskrete Zufallsgröße. | ||
| − | + | Reduzierte Informationen erhält man durch die so genannten Momente $m_k$, wobei $k$ eine natürliche Zahl darstellt. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Zwei alternative Berechnungsmöglichkeiten:}$ | ||
| − | + | Unter der hier stillschweigend vorausgesetzten Bedingung [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Ergodische_Zufallsprozesse|"Ergodizität"]] gibt es für das Moment $k$-ter Ordnung zwei unterschiedliche Berechnungsmöglichkeiten: | |
| + | *die '''Scharmittelung''' bzw. "Erwartungswertbildung" ⇒ Mittelung über alle möglichen Werte $\{ z_\mu\}$ mit der Laufvariablen $\mu = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , M$: | ||
| + | :$$m_k = {\rm E} \big[z^k \big] = \sum_{\mu = 1}^{M}p_\mu \cdot z_\mu^k \hspace{2cm} \rm mit \hspace{0.1cm} {\rm E\big[\text{ ...} \big]\hspace{-0.1cm}:} \hspace{0.3cm} \rm Erwartungswert ;$$ | ||
| + | *die '''Zeitmittelung''' über die Zufallsfolge $\langle z_ν\rangle$ mit der Laufvariablen $ν = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , N$: | ||
| + | :$$m_k=\overline{z_\nu^k}=\hspace{0.01cm}\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=\rm 1}^{\it N}z_\nu^k\hspace{1.7cm}\rm mit\hspace{0.1cm}\ddot{u}berstreichender\hspace{0.1cm}Linie\hspace{-0.1cm}:\hspace{0.1cm}Zeitmittelwert.$$}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Anzumerken ist: | |
| − | + | *Beide Berechnungsarten führen bei genügend großen Werten von $N$ zum gleichen asymptotischen Ergebnis. | |
| − | $$ | + | *Bei endlichem $N$ ergibt sich ein vergleichbarer Fehler, als wenn die Wahrscheinlichkeit durch die relative Häufigkeit angenähert wird. |
| − | |||
| − | [[ | + | ==Moment erster Ordnung – Linearer Mittelwert – Gleichanteil== |
| + | <br> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ Mit $k = 1$ erhält man aus der allgemeinen Gleichung das Moment erster Ordnung ⇒ den '''linearen Mittelwert''' (englisch: "mean"): | ||
| + | :$$m_1 =\sum_{\mu=1}^{M}p_\mu\cdot z_\mu =\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=1}^{N}z_\nu.$$ | ||
| + | *Der linke Teil dieser Gleichung beschreibt die Scharmittelung (über alle möglichen Werte), | ||
| + | :während die rechte Gleichung die Bestimmung als Zeitmittelwert angibt. | ||
| + | *In Zusammenhang mit Signalen wird diese Größe auch als der [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals|Gleichanteil]] bezeichnet.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | [[Datei:P_ID49__Sto_T_2_2_S2_neu.png|right|frame|Gleichanteil $m_1$ eines Binärsignals]] |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Beispiel 1:}$ Ein Binärsignal $x(t)$ mit den beiden möglichen Amplitudenwerten | ||
| + | *$1\hspace{0.03cm}\rm V$ $($für das Symbol $\rm L)$, | ||
| + | *$3\hspace{0.03cm}\rm V$ $($für das Symbol $\rm H)$ | ||
| + | sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ besitzt den linearen Mittelwert (Gleichanteil ) | ||
| + | :$$m_1 = 0.2 \cdot 1\,{\rm V}+ 0.8 \cdot 3\,{\rm V}= 2.6 \,{\rm V}. $$ | ||
| + | Dieser ist in der Grafik als rote Linie eingezeichnet. | ||
| + | Bestimmt man diese Kenngröße durch Zeitmittelung über die dargestellten $N = 12$ Signalwerte, so erhält man einen etwas kleineren Wert: | ||
| + | :$$m_1\hspace{0.01cm}' = 4/12 \cdot 1\,{\rm V}+ 8/12 \cdot 3\,{\rm V}= 2.33 \,{\rm V}. $$ | ||
| + | Hier wurden die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ durch die entsprechenden Häufigkeiten $h_{\rm L} = 4/12$ und $h_{\rm H} = 8/12$ ersetzt. Der relative Fehler aufgrund der unzureichenden Folgenlänge $N$ ist im Beispiel größer als $10\%$. | ||
| + | $\text{Hinweis zu unserer (zugegebenermaßen etwas ungewöhnlicher) Nomenklatur:}$ | ||
| + | Wir bezeichnen hier Binärsymbole wie in der Schaltungstechnik mit $\rm L$ ("Low") und $\rm H$ ("High"), um Verwechslungen zu vermeiden. | ||
| + | *In der Codierungstheorie wird sinnvollerweise $\{ \text{L, H}\}$ auf $\{0, 1\}$ abgebildet, um die Möglichkeiten der Modulo-Algebra nutzen zu können. | ||
| + | *Zur Beschreibung der Modulation mit bipolaren (antipodalen) Signalen wählt man dagegen besser die Zuordnung $\{ \text{L, H}\}$ ⇔ $ \{-1, +1\}$. | ||
| + | }} | ||
| + | |||
| + | ==Moment zweiter Ordnung – Leistung – Varianz – Streuung== | ||
| + | <br> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definitionen:}$ | ||
| + | |||
| + | *Analog zum linearen Mittelwert erhält man mit $k = 2$ das '''Moment zweiter Ordnung''' (englisch: "second order moment"): | ||
| + | :$$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$ | ||
| + | |||
| + | *Zusammen mit dem Gleichanteil $m_1$ kann daraus als weitere Kenngröße die '''Varianz''' (englisch: "variance") $σ^2$ bestimmt werden ("Satz von Steiner"): | ||
| + | :$$\sigma^2=m_2-m_1^2.$$ | ||
| + | *Die '''Streuung''' $σ$ ist die Quadratwurzel der Varianz; manchmal wird diese Größe auch "Standardabweichung" (englisch: "standard deviation") genannt: | ||
| + | :$$\sigma=\sqrt{m_2-m_1^2}.$$}} | ||
| + | |||
| + | |||
| + | $\text{Hinweise zu den Einheiten:}$ | ||
| + | |||
| + | #Bei einem Zufallssignal $x(t)$ gibt $m_2$ die gesamte Leistung (Gleichleistung plus Wechselleitung) an, bezogen auf den Widerstand $1 \hspace{0.03cm} Ω$. | ||
| + | #Beschreibt $x(t)$ einen Spannungsverlauf, so besitzt dementsprechend $m_2$ die Einheit ${\rm V}^2$ und der Effektivwert (englisch: "root mean square") $x_{\rm eff}=\sqrt{m_2}$ die Einheit ${\rm V}$. Die Gesamtleistung für beliebigen Bezugswiderstand $R$ berechnet sich zu $P=m_2/R$ und besitzt dementsprechend die Einheit $\rm V^2/(V/A) = W$. | ||
| + | #Beschreibt $x(t)$ einen Stromverlauf, so hat $m_2$ die Einheit ${\rm A}^2$ und der Effektivwert $x_{\rm eff}=\sqrt{m_2}$ die Einheit ${\rm A}$. Die Gesamtleistung für beliebigen Bezugswiderstand $R$ berechnet sich zu $P=m_2\cdot R$ und besitzt dementsprechend die Einheit $\rm A^2 \cdot(V/A) = W$. | ||
| + | #Nur im Sonderfall $m_1=0$ ist die Varianz $σ^2=m_2$. Dann stimmt auch die Standardabweichung $σ$ mit dem Effektivwert $x_{\rm eff}$ überein. | ||
| + | |||
| + | |||
| + | Das Lernvideo [[Momentenberechnung bei diskreten Zufallsgrößen (Lernvideo)|Momentenberechnung bei diskreten Zufallsgrößen]] verdeutlicht die definierten Größen am Beispiel eines Digitalsignals. | ||
| + | |||
| + | [[Datei:P_ID456__Sto_T_2_2_S3_neu.png | right|frame|Standardabweichung eines Binärsignals]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ | ||
| + | Bei einem Binärsignal $x(t)$ mit den Amplitudenwerten | ||
| + | *$1\hspace{0.03cm}\rm V$ $($für das Symbol $\rm L)$, | ||
| + | *$3\hspace{0.03cm}\rm V$ $($für das Symbol $\rm H)$ | ||
| + | |||
| + | |||
| + | sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ ergibt sich für das zweite Moment: | ||
| + | :$$m_2 = 0.2 \cdot (1\,{\rm V})^2+ 0.8 \cdot (3\,{\rm V})^2 = 7.4 \hspace{0.1cm}{\rm V}^2,$$ | ||
| + | |||
| + | Der Effektivwert $x_{\rm eff}=\sqrt{m_2}=2.72\,{\rm V}$ ist unabhängig vom Bezugswiderstand $R$ im Gegensatz zur Gesamtleistung. Für diese ergibt sich mit $R=1 \hspace{0.1cm} Ω$ der Wert $P=7.4 \hspace{0.1cm}{\rm W}$, mit $R=50 \hspace{0.1cm} Ω$ dagegen nur $P=0.148 \hspace{0.1cm}{\rm W}$. | ||
| + | |||
| + | Mit dem Gleichanteil $m_1 = 2.6 \hspace{0.05cm}\rm V$ $($siehe [[Stochastische_Signaltheorie/Momente_einer_diskreten_Zufallsgröße#Linearer_Mittelwert_-_Gleichanteil|$\text{Beispiel 1})$]] folgt daraus für | ||
| + | *die Varianz $ σ^2 = 7.4 \hspace{0.05cm}{\rm V}^2 - \big [2.6 \hspace{0.05cm}\rm V\big ]^2 = 0.64\hspace{0.05cm} {\rm V}^2$, | ||
| + | *die Standardabweichung (Streuung) $σ = 0.8 \hspace{0.05cm} \rm V$. | ||
| + | |||
| + | |||
| + | Die gleiche Varianz $ σ^2 = 0.64\hspace{0.05cm} {\rm V}^2$ und die gleiche Standardabweichung $σ = 0.8 \hspace{0.05cm} \rm V$ ergeben sich für die Amplituden $0\hspace{0.05cm}\rm V$ $($für das Symbol $\rm L)$ und $2\hspace{0.05cm}\rm V$ $($für das Symbol $\rm H)$, vorausgesetzt, die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ und $p_{\rm H} = 0.8$ bleiben gleich. Nur der Gleichanteil und die Gesamtleistung ändern sich: | ||
| + | :$$m_1 = 1.6 \hspace{0.05cm}{\rm V}, $$ | ||
| + | :$$P = {m_1}^2 +\sigma^2 = 3.2 \hspace{0.05cm}{\rm V}^2.$$}} | ||
| + | |||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:2.2 Mehrstufensignale|Aufgabe 2.2: Mehrstufensignale]] | ||
| + | |||
| + | [[Aufgaben:2.2Z_Diskrete_Zufallsgrößen|Aufgabe 2.2Z: Diskrete Zufallsgrößen]] | ||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 18. Februar 2022, 14:26 Uhr
Inhaltsverzeichnis
Berechnung als Schar- bzw. Zeitmittelwert
Die Wahrscheinlichkeiten und die relativen Häufigkeiten liefern weitreichende Informationen über eine diskrete Zufallsgröße.
Reduzierte Informationen erhält man durch die so genannten Momente $m_k$, wobei $k$ eine natürliche Zahl darstellt.
$\text{Zwei alternative Berechnungsmöglichkeiten:}$
Unter der hier stillschweigend vorausgesetzten Bedingung "Ergodizität" gibt es für das Moment $k$-ter Ordnung zwei unterschiedliche Berechnungsmöglichkeiten:
- die Scharmittelung bzw. "Erwartungswertbildung" ⇒ Mittelung über alle möglichen Werte $\{ z_\mu\}$ mit der Laufvariablen $\mu = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , M$:
- $$m_k = {\rm E} \big[z^k \big] = \sum_{\mu = 1}^{M}p_\mu \cdot z_\mu^k \hspace{2cm} \rm mit \hspace{0.1cm} {\rm E\big[\text{ ...} \big]\hspace{-0.1cm}:} \hspace{0.3cm} \rm Erwartungswert ;$$
- die Zeitmittelung über die Zufallsfolge $\langle z_ν\rangle$ mit der Laufvariablen $ν = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , N$:
- $$m_k=\overline{z_\nu^k}=\hspace{0.01cm}\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=\rm 1}^{\it N}z_\nu^k\hspace{1.7cm}\rm mit\hspace{0.1cm}\ddot{u}berstreichender\hspace{0.1cm}Linie\hspace{-0.1cm}:\hspace{0.1cm}Zeitmittelwert.$$
Anzumerken ist:
- Beide Berechnungsarten führen bei genügend großen Werten von $N$ zum gleichen asymptotischen Ergebnis.
- Bei endlichem $N$ ergibt sich ein vergleichbarer Fehler, als wenn die Wahrscheinlichkeit durch die relative Häufigkeit angenähert wird.
Moment erster Ordnung – Linearer Mittelwert – Gleichanteil
$\text{Definition:}$ Mit $k = 1$ erhält man aus der allgemeinen Gleichung das Moment erster Ordnung ⇒ den linearen Mittelwert (englisch: "mean"):
- $$m_1 =\sum_{\mu=1}^{M}p_\mu\cdot z_\mu =\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=1}^{N}z_\nu.$$
- Der linke Teil dieser Gleichung beschreibt die Scharmittelung (über alle möglichen Werte),
- während die rechte Gleichung die Bestimmung als Zeitmittelwert angibt.
- In Zusammenhang mit Signalen wird diese Größe auch als der Gleichanteil bezeichnet.
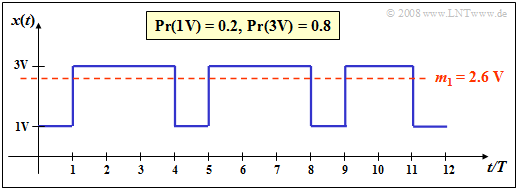
$\text{Beispiel 1:}$ Ein Binärsignal $x(t)$ mit den beiden möglichen Amplitudenwerten
- $1\hspace{0.03cm}\rm V$ $($für das Symbol $\rm L)$,
- $3\hspace{0.03cm}\rm V$ $($für das Symbol $\rm H)$
sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ besitzt den linearen Mittelwert (Gleichanteil )
- $$m_1 = 0.2 \cdot 1\,{\rm V}+ 0.8 \cdot 3\,{\rm V}= 2.6 \,{\rm V}. $$
Dieser ist in der Grafik als rote Linie eingezeichnet.
Bestimmt man diese Kenngröße durch Zeitmittelung über die dargestellten $N = 12$ Signalwerte, so erhält man einen etwas kleineren Wert:
- $$m_1\hspace{0.01cm}' = 4/12 \cdot 1\,{\rm V}+ 8/12 \cdot 3\,{\rm V}= 2.33 \,{\rm V}. $$
Hier wurden die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ durch die entsprechenden Häufigkeiten $h_{\rm L} = 4/12$ und $h_{\rm H} = 8/12$ ersetzt. Der relative Fehler aufgrund der unzureichenden Folgenlänge $N$ ist im Beispiel größer als $10\%$.
$\text{Hinweis zu unserer (zugegebenermaßen etwas ungewöhnlicher) Nomenklatur:}$
Wir bezeichnen hier Binärsymbole wie in der Schaltungstechnik mit $\rm L$ ("Low") und $\rm H$ ("High"), um Verwechslungen zu vermeiden.
- In der Codierungstheorie wird sinnvollerweise $\{ \text{L, H}\}$ auf $\{0, 1\}$ abgebildet, um die Möglichkeiten der Modulo-Algebra nutzen zu können.
- Zur Beschreibung der Modulation mit bipolaren (antipodalen) Signalen wählt man dagegen besser die Zuordnung $\{ \text{L, H}\}$ ⇔ $ \{-1, +1\}$.
Moment zweiter Ordnung – Leistung – Varianz – Streuung
$\text{Definitionen:}$
- Analog zum linearen Mittelwert erhält man mit $k = 2$ das Moment zweiter Ordnung (englisch: "second order moment"):
- $$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$
- Zusammen mit dem Gleichanteil $m_1$ kann daraus als weitere Kenngröße die Varianz (englisch: "variance") $σ^2$ bestimmt werden ("Satz von Steiner"):
- $$\sigma^2=m_2-m_1^2.$$
- Die Streuung $σ$ ist die Quadratwurzel der Varianz; manchmal wird diese Größe auch "Standardabweichung" (englisch: "standard deviation") genannt:
- $$\sigma=\sqrt{m_2-m_1^2}.$$
$\text{Hinweise zu den Einheiten:}$
- Bei einem Zufallssignal $x(t)$ gibt $m_2$ die gesamte Leistung (Gleichleistung plus Wechselleitung) an, bezogen auf den Widerstand $1 \hspace{0.03cm} Ω$.
- Beschreibt $x(t)$ einen Spannungsverlauf, so besitzt dementsprechend $m_2$ die Einheit ${\rm V}^2$ und der Effektivwert (englisch: "root mean square") $x_{\rm eff}=\sqrt{m_2}$ die Einheit ${\rm V}$. Die Gesamtleistung für beliebigen Bezugswiderstand $R$ berechnet sich zu $P=m_2/R$ und besitzt dementsprechend die Einheit $\rm V^2/(V/A) = W$.
- Beschreibt $x(t)$ einen Stromverlauf, so hat $m_2$ die Einheit ${\rm A}^2$ und der Effektivwert $x_{\rm eff}=\sqrt{m_2}$ die Einheit ${\rm A}$. Die Gesamtleistung für beliebigen Bezugswiderstand $R$ berechnet sich zu $P=m_2\cdot R$ und besitzt dementsprechend die Einheit $\rm A^2 \cdot(V/A) = W$.
- Nur im Sonderfall $m_1=0$ ist die Varianz $σ^2=m_2$. Dann stimmt auch die Standardabweichung $σ$ mit dem Effektivwert $x_{\rm eff}$ überein.
Das Lernvideo Momentenberechnung bei diskreten Zufallsgrößen verdeutlicht die definierten Größen am Beispiel eines Digitalsignals.
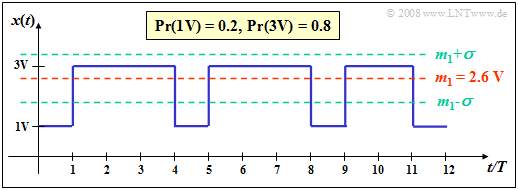
$\text{Beispiel 2:}$ Bei einem Binärsignal $x(t)$ mit den Amplitudenwerten
- $1\hspace{0.03cm}\rm V$ $($für das Symbol $\rm L)$,
- $3\hspace{0.03cm}\rm V$ $($für das Symbol $\rm H)$
sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ ergibt sich für das zweite Moment:
- $$m_2 = 0.2 \cdot (1\,{\rm V})^2+ 0.8 \cdot (3\,{\rm V})^2 = 7.4 \hspace{0.1cm}{\rm V}^2,$$
Der Effektivwert $x_{\rm eff}=\sqrt{m_2}=2.72\,{\rm V}$ ist unabhängig vom Bezugswiderstand $R$ im Gegensatz zur Gesamtleistung. Für diese ergibt sich mit $R=1 \hspace{0.1cm} Ω$ der Wert $P=7.4 \hspace{0.1cm}{\rm W}$, mit $R=50 \hspace{0.1cm} Ω$ dagegen nur $P=0.148 \hspace{0.1cm}{\rm W}$.
Mit dem Gleichanteil $m_1 = 2.6 \hspace{0.05cm}\rm V$ $($siehe $\text{Beispiel 1})$ folgt daraus für
- die Varianz $ σ^2 = 7.4 \hspace{0.05cm}{\rm V}^2 - \big [2.6 \hspace{0.05cm}\rm V\big ]^2 = 0.64\hspace{0.05cm} {\rm V}^2$,
- die Standardabweichung (Streuung) $σ = 0.8 \hspace{0.05cm} \rm V$.
Die gleiche Varianz $ σ^2 = 0.64\hspace{0.05cm} {\rm V}^2$ und die gleiche Standardabweichung $σ = 0.8 \hspace{0.05cm} \rm V$ ergeben sich für die Amplituden $0\hspace{0.05cm}\rm V$ $($für das Symbol $\rm L)$ und $2\hspace{0.05cm}\rm V$ $($für das Symbol $\rm H)$, vorausgesetzt, die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ und $p_{\rm H} = 0.8$ bleiben gleich. Nur der Gleichanteil und die Gesamtleistung ändern sich:
- $$m_1 = 1.6 \hspace{0.05cm}{\rm V}, $$
- $$P = {m_1}^2 +\sigma^2 = 3.2 \hspace{0.05cm}{\rm V}^2.$$
Aufgaben zum Kapitel
Aufgabe 2.2: Mehrstufensignale
Aufgabe 2.2Z: Diskrete Zufallsgrößen