Aufgaben:Aufgabe 4.5: 2D-Prüfungsauswertung: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Zweidimensionale Gaußsche Zufallsgrößen }} right| :In einer Studie wu…“) |
|||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
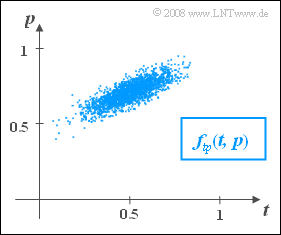
| − | [[Datei:P_ID267__Sto_A_4_5.png|right|]] | + | [[Datei:P_ID267__Sto_A_4_5.png|right|frame|Gegebene Gaußsche 2D-WDF $f_{tp}(t,\hspace{0.08cm}p)$]] |
| − | + | In einer Studie wurden die Meisterprüfungen für das Handwerk untersucht, die sich stets aus einem theoretischen und zusätzlich einem praktischen Teil zusammensetzen. In der Grafik bezeichnet | |
| + | * $t$ die Punktzahl in der theoretischen Prüfung, | ||
| + | * $p$ die Punktzahl in der praktischen Prüfung. | ||
| − | |||
| − | + | Beide Zufallsgrößen $(t$ und $p)$ sind dabei jeweils auf die Maximalpunktzahlen normiert und können deshalb nur Werte zwischen $0$ und $1$ annehmen. | |
| − | + | Beide Zufallsgrößen sind zudem als kontinuierliche Zufallsgrößen zu interpretieren, das heißt: $t$ und $p$ sind nicht auf diskrete Zahlenwerte beschränkt. | |
| − | + | *Die Grafik zeigt die WDF $f_{tp}(t,\hspace{0.08cm} p)$ der zweidimensionalen Zufallsgröße $(t,\hspace{0.08cm} p)$, die nach der Auswertung von insgesamt $N = 10\hspace{0.08cm}000$ Abschlussarbeiten veröffentlicht wurde. | |
| + | *Diese Funktion wurde mit Hilfe eines Auswertungsprogramms empirisch wie folgt angenähert: | ||
| + | :$$f_{tp}(t,\hspace{0.08cm}p) = \rm 13.263\cdot \rm exp \Bigg\{-\frac{(\it t - \rm 0.5)^{\rm 2}}{\rm 0.0288}-\frac{(\it p-\rm 0.7)^{\rm 2}}{\rm 0.0072} + \frac{(\it t-\rm 0.5)(\it p-\rm 0.7)}{\rm 0.0090}\Bigg\}.$$ | ||
| − | |||
| − | |||
| − | : | + | |
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen|Zweidimensionale Gaußsche Zufallsgrößen]]. | ||
| + | |||
| + | *Weitere Informationen zu dieser Thematik liefert das Lernvideo [[Gaußsche_2D-Zufallsgrößen_(Lernvideo)|Gaußsche 2D-Zufallsgrößen]]: | ||
| + | ::Teil 1: Gaußsche Zufallsgrößen ohne statistische Bindungen, | ||
| + | ::Teil 2: Gaußsche Zufallsgrößen mit statistischen Bindungen. | ||
| + | |||
| Zeile 23: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist der Mittelwert der im Theorieteil erzielten Ergebnisse? | + | {Wie groß ist der Mittelwert $m_t$ der im Theorieteil erzielten Ergebnisse? |
|type="{}"} | |type="{}"} | ||
| − | $m_t$ | + | $m_t \ = \ $ { 0.5 3% } |
| − | {Wie groß ist der Mittelwert der im Praxisteilteil erzielten Ergebnisse? Geben Sie auch die WDF der mittelwertfreien Zufallsgröße ( | + | {Wie groß ist der Mittelwert $m_p$ der im Praxisteilteil erzielten Ergebnisse? Geben Sie auch die WDF der mittelwertfreien Zufallsgröße $(t\hspace{0.05cm}',\hspace{0.08cm} p\hspace{0.05cm}')$ an. |
|type="{}"} | |type="{}"} | ||
| − | $m_p$ | + | $m_p \ = \ $ { 0.7 3% } |
| − | {Berechnen Sie die Streuungen (Standardabweichungen) | + | {Berechnen Sie die Streuungen (Standardabweichungen) $\sigma_t$ und $\sigma_p$ sowie den Korrelationskoeffizienten $\rho$ zwischen den beiden Größen. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_t$ | + | $\sigma_t \ = \ $ { 0.2 3% } |
| − | $\sigma_p$ | + | $\sigma_p \ = \ $ { 0.1 3% } |
| − | $\rho$ | + | $\rho \ = \ $ { 0.8 3% } |
| − | {Welche der | + | {Welche der folgenden Aussagen sind zutreffend? |
|type="[]"} | |type="[]"} | ||
+ Der Gauß-Ansatz ist für dieses Problem nur eine Näherung. | + Der Gauß-Ansatz ist für dieses Problem nur eine Näherung. | ||
| − | - War ein Prüfling im Theoretieteil überdurchschnittlich gut, so ist zu erwarten, dass er in der Praxis eher schlecht ist. | + | - War ein Prüfling im Theoretieteil überdurchschnittlich gut, so ist zu erwarten, dass er in der Praxis eher schlecht ist. |
| − | {Mit welcher Wahrscheinlichkeit hat ein Teilnehmer in der Theorie– und der Praxis–Prüfung jeweils zwischen 49% und 51% der Punkte erreicht? | + | {Mit welcher Wahrscheinlichkeit hat ein Teilnehmer in der Theorie– und der Praxis–Prüfung jeweils zwischen $49\%$ und $51\%$ der Punkte erreicht? |
|type="{}"} | |type="{}"} | ||
| − | $Pr[(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)]$ | + | ${\rm Pr}\big [(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)\big]\ = \ $ { 2 3% } $\ \cdot 10^{-5}$ |
| Zeile 55: | Zeile 63: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' und '''(2)''' | |
| − | :$$f_{\it t'p'}(\it t', \it p') = \rm 13.263\cdot \rm exp\Bigg (-\frac{\it t'^{\rm 2}}{\rm 0.0288} - \frac{\it p'^{\rm 2}}{\rm 0.0072}+\frac{\it t'\cdot p'}{\rm 0.0090}\Bigg ). $$ | + | *Die Mittelwerte $m_t\hspace{0.15cm}\underline{= 0.5}$ und $m_p\hspace{0.15cm}\underline{= 0.7}$ können aus der Skizze abgeschätzt und aus der angegebenen Gleichung exakt ermittelt werden. |
| + | *Die 2D–WDF der mittelwertfreien Größe lautet: | ||
| + | :$$f_{\it t\hspace{0.05cm}'\hspace{0.05cm}p\hspace{0.05cm}'}(\it t\hspace{0.05cm}',\hspace{0.08cm} \it p\hspace{0.05cm}'{\rm )} = \rm 13.263\cdot \rm exp\Bigg (-\frac{\it {\rm (}t\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0288} - \frac{\it {\rm (}p\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0072}+\frac{\it t\hspace{0.05cm}'\cdot p\hspace{0.05cm}'}{\rm 0.0090}\Bigg ). $$ | ||
| + | *Zur Vereinfachung wird im Folgenden auf den Apostroph zur Kennzeichnung mittelwertfreier Größen verzichtet. | ||
| + | *Sowohl $t$ als auch $p$ sind bis einschließlich der Teilaufgabe '''(4)''' als mittelwertfrei zu verstehen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(3)''' Die allgemeine Gleichung einer mittelwertfreien 2D-Zufallsgröße lautet: | |
| − | :$$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm | + | :$$f_{\it tp}(\it t,\hspace{0.08cm} \it p)=\frac{\rm 1}{\rm 2\it \pi \cdot \sigma_{\it t}\cdot \sigma_{\it p} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 2\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it t}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{ (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it t}\cdot\sigma_{\it p}}\Bigg\}.$$ |
| − | |||
| − | : | + | *Die Standardabweichungen $\sigma_t$ und $\sigma_p$ sowie der Korrelationskoeffizient $\rho$ lassen sich durch Koeffizientenvergleich ermitteln: |
| − | :$$\rm 2\cdot(\rm 1-\it\rho^{\rm 2})\cdot\it\sigma_{\it p}^{\rm 2} | + | *Ein Vergleich der beiden ersten Terme im Exponenten zeigt, dass $\sigma_t = 2 \cdot \sigma_p$ gelten muss. Damit lautet die WDF: |
| − | + | :$$f_{\it tp}(\it t,\hspace{0.08cm} \it p)=\frac{\rm 1}{\rm 4\it \pi \cdot \sigma_{\it p}^{\rm 2} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 8\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it p}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{\rm 2\cdot (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it p}^{\rm 2}}\Bigg\}.$$ | |
| − | + | *Aus dem zweiten Term des Exponenten folgt: | |
| + | :$$2\cdot(1-\rho^{\rm 2})\cdot\sigma_{p}^{ 2}=0.0072\hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{p}^{2} = \frac{ 0.0036}{(1-\rho^{\rm 2})}.$$ | ||
| + | *Der Faktor $K = 13.263$ liefert nun das Ergebnis | ||
:$$K = \frac{\sqrt{\rm 1-\it\rho^{\rm 2}}}{\rm 4\it\pi\cdot \rm 0.0036}=\rm 13.263 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sqrt{\rm 1-\it\rho^{\rm 2}}=\rm 0.6 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\hspace{0.15cm}\underline{ \rm \rho = \rm 0.8}.$$ | :$$K = \frac{\sqrt{\rm 1-\it\rho^{\rm 2}}}{\rm 4\it\pi\cdot \rm 0.0036}=\rm 13.263 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sqrt{\rm 1-\it\rho^{\rm 2}}=\rm 0.6 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\hspace{0.15cm}\underline{ \rm \rho = \rm 0.8}.$$ | ||
| + | *Daraus ergeben sich die Streuungen zu $\sigma_t\hspace{0.15cm}\underline{= 0.2}$ und $\sigma_p\hspace{0.15cm}\underline{= 0.1}$. | ||
| + | |||
| + | *Zur Kontrolle verwenden wir den letzten Term des Exponenten: | ||
| + | :$$\frac{(1 - \rho^{2})\cdot \sigma_{\it t}\cdot\sigma_{\it p}}{\it \rho} = \frac{0.36\cdot 0.1\cdot 0.2}{0.8} = \rm 0.009.$$ | ||
| + | *Dies stimmt mit dem vorgegebenen Wert überein. | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' Der <u>Lösungsvorschlag 1</u> ist richtig. | |
| + | *Im Grunde genommen ist $(t,\hspace{0.08cm} p)$ keine echte Gaußsche Zufallsgröße, da beide Komponenten begrenzt sind. | ||
| + | *Die Wahrscheinlichkeiten für die Ereignisse $t < 0$, $t >1$, $p < 0$ und $p >1$ sind somit Null. | ||
| + | *Bei Gaußschen Größen mit den hier vorliegenden Mittelwerten und Streuungen ergeben sich jedoch | ||
:$$\rm Pr(\it t < \rm 0) = \rm Pr(\it t > \rm 1) = \rm Q(2.5)\approx 6\cdot 10^{-3},$$ | :$$\rm Pr(\it t < \rm 0) = \rm Pr(\it t > \rm 1) = \rm Q(2.5)\approx 6\cdot 10^{-3},$$ | ||
:$$\rm Pr(\it p > \rm 1) = \rm Q(3)\approx 1.3\cdot 10^{-3},$$ | :$$\rm Pr(\it p > \rm 1) = \rm Q(3)\approx 1.3\cdot 10^{-3},$$ | ||
:$$\rm Pr(\it p < \rm 0) = \rm Q(7)\approx 10^{-12}.$$ | :$$\rm Pr(\it p < \rm 0) = \rm Q(7)\approx 10^{-12}.$$ | ||
| − | + | *Der Korrelationskoeffizient $\rho = 0.8$ ist hier positiv: Hat der Prüfling im Theorieteil eher gut abgeschnitten, so ist (zumindest bei dieser Aufgabe) zu erwarten, dass auch der praktische Teil gut läuft. | |
| + | *Hier ist also der Lösungsvorschlag 2 falsch. In der Praxis ist das sicher nicht immer so. | ||
| + | |||
| + | |||
| − | + | '''(5)''' Für diese Wahrscheinlichkeit gilt mit $\Delta t = \Delta p = 0.02$: | |
| − | :$$\rm Pr\ | + | :$$\rm Pr\left [( \rm 0.5-\frac{\rm\Delta\it t}{\rm 2}\le \it t \le \rm 0.5+\frac{\rm\Delta\it t}{\rm 2})\cap(\rm 0.5-\frac{\rm\Delta\it p}{\rm 2}\le \it p \le \rm 0.5+\frac{\rm\Delta\it p}{\rm 2})\right ] \approx \rm\Delta\it t\cdot\rm\Delta\it p\cdot \it f_{tp}{\rm (}t=\rm 0.5,\hspace{0.08cm} \it p = \rm 0.5).$$ |
| − | |||
| − | + | *Für die 2D-WDF gilt unter Berücksichtigung der Mittelwerte $m_t{= 0.5}$ und $m_p{= 0.7}$: | |
| − | :$$f_{tp}(\it t=\rm 0.5, \it p=\rm 0.5) = \rm 13.263\cdot | + | :$$f_{tp}(\it t=\rm 0.5,\hspace{0.08cm} \it p=\rm 0.5) = \rm 13.263\cdot {\rm e}^{-(-0.2)^2/0.0072}\approx 0.0513.$$ |
| − | + | *Damit ergibt sich die gesuchte Wahrscheinlichkeit zu | |
| + | :$${\rm Pr}\big[(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)\big] =0.02 \cdot 0.02 \cdot 0.0513\hspace{0.15cm}\underline{\approx 2 · 10^{-5}}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Stochastische Signaltheorie|^4.2 | + | [[Category:Aufgaben zu Stochastische Signaltheorie|^4.2 Gaußsche 2D-Zufallsgrößen^]] |
Aktuelle Version vom 24. Februar 2022, 16:40 Uhr
In einer Studie wurden die Meisterprüfungen für das Handwerk untersucht, die sich stets aus einem theoretischen und zusätzlich einem praktischen Teil zusammensetzen. In der Grafik bezeichnet
- $t$ die Punktzahl in der theoretischen Prüfung,
- $p$ die Punktzahl in der praktischen Prüfung.
Beide Zufallsgrößen $(t$ und $p)$ sind dabei jeweils auf die Maximalpunktzahlen normiert und können deshalb nur Werte zwischen $0$ und $1$ annehmen.
Beide Zufallsgrößen sind zudem als kontinuierliche Zufallsgrößen zu interpretieren, das heißt: $t$ und $p$ sind nicht auf diskrete Zahlenwerte beschränkt.
- Die Grafik zeigt die WDF $f_{tp}(t,\hspace{0.08cm} p)$ der zweidimensionalen Zufallsgröße $(t,\hspace{0.08cm} p)$, die nach der Auswertung von insgesamt $N = 10\hspace{0.08cm}000$ Abschlussarbeiten veröffentlicht wurde.
- Diese Funktion wurde mit Hilfe eines Auswertungsprogramms empirisch wie folgt angenähert:
- $$f_{tp}(t,\hspace{0.08cm}p) = \rm 13.263\cdot \rm exp \Bigg\{-\frac{(\it t - \rm 0.5)^{\rm 2}}{\rm 0.0288}-\frac{(\it p-\rm 0.7)^{\rm 2}}{\rm 0.0072} + \frac{(\it t-\rm 0.5)(\it p-\rm 0.7)}{\rm 0.0090}\Bigg\}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Gaußsche Zufallsgrößen.
- Weitere Informationen zu dieser Thematik liefert das Lernvideo Gaußsche 2D-Zufallsgrößen:
- Teil 1: Gaußsche Zufallsgrößen ohne statistische Bindungen,
- Teil 2: Gaußsche Zufallsgrößen mit statistischen Bindungen.
Fragebogen
Musterlösung
(1) und (2)
- Die Mittelwerte $m_t\hspace{0.15cm}\underline{= 0.5}$ und $m_p\hspace{0.15cm}\underline{= 0.7}$ können aus der Skizze abgeschätzt und aus der angegebenen Gleichung exakt ermittelt werden.
- Die 2D–WDF der mittelwertfreien Größe lautet:
- $$f_{\it t\hspace{0.05cm}'\hspace{0.05cm}p\hspace{0.05cm}'}(\it t\hspace{0.05cm}',\hspace{0.08cm} \it p\hspace{0.05cm}'{\rm )} = \rm 13.263\cdot \rm exp\Bigg (-\frac{\it {\rm (}t\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0288} - \frac{\it {\rm (}p\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0072}+\frac{\it t\hspace{0.05cm}'\cdot p\hspace{0.05cm}'}{\rm 0.0090}\Bigg ). $$
- Zur Vereinfachung wird im Folgenden auf den Apostroph zur Kennzeichnung mittelwertfreier Größen verzichtet.
- Sowohl $t$ als auch $p$ sind bis einschließlich der Teilaufgabe (4) als mittelwertfrei zu verstehen.
(3) Die allgemeine Gleichung einer mittelwertfreien 2D-Zufallsgröße lautet:
- $$f_{\it tp}(\it t,\hspace{0.08cm} \it p)=\frac{\rm 1}{\rm 2\it \pi \cdot \sigma_{\it t}\cdot \sigma_{\it p} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 2\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it t}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{ (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it t}\cdot\sigma_{\it p}}\Bigg\}.$$
- Die Standardabweichungen $\sigma_t$ und $\sigma_p$ sowie der Korrelationskoeffizient $\rho$ lassen sich durch Koeffizientenvergleich ermitteln:
- Ein Vergleich der beiden ersten Terme im Exponenten zeigt, dass $\sigma_t = 2 \cdot \sigma_p$ gelten muss. Damit lautet die WDF:
- $$f_{\it tp}(\it t,\hspace{0.08cm} \it p)=\frac{\rm 1}{\rm 4\it \pi \cdot \sigma_{\it p}^{\rm 2} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 8\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it p}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{\rm 2\cdot (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it p}^{\rm 2}}\Bigg\}.$$
- Aus dem zweiten Term des Exponenten folgt:
- $$2\cdot(1-\rho^{\rm 2})\cdot\sigma_{p}^{ 2}=0.0072\hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{p}^{2} = \frac{ 0.0036}{(1-\rho^{\rm 2})}.$$
- Der Faktor $K = 13.263$ liefert nun das Ergebnis
- $$K = \frac{\sqrt{\rm 1-\it\rho^{\rm 2}}}{\rm 4\it\pi\cdot \rm 0.0036}=\rm 13.263 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sqrt{\rm 1-\it\rho^{\rm 2}}=\rm 0.6 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\hspace{0.15cm}\underline{ \rm \rho = \rm 0.8}.$$
- Daraus ergeben sich die Streuungen zu $\sigma_t\hspace{0.15cm}\underline{= 0.2}$ und $\sigma_p\hspace{0.15cm}\underline{= 0.1}$.
- Zur Kontrolle verwenden wir den letzten Term des Exponenten:
- $$\frac{(1 - \rho^{2})\cdot \sigma_{\it t}\cdot\sigma_{\it p}}{\it \rho} = \frac{0.36\cdot 0.1\cdot 0.2}{0.8} = \rm 0.009.$$
- Dies stimmt mit dem vorgegebenen Wert überein.
(4) Der Lösungsvorschlag 1 ist richtig.
- Im Grunde genommen ist $(t,\hspace{0.08cm} p)$ keine echte Gaußsche Zufallsgröße, da beide Komponenten begrenzt sind.
- Die Wahrscheinlichkeiten für die Ereignisse $t < 0$, $t >1$, $p < 0$ und $p >1$ sind somit Null.
- Bei Gaußschen Größen mit den hier vorliegenden Mittelwerten und Streuungen ergeben sich jedoch
- $$\rm Pr(\it t < \rm 0) = \rm Pr(\it t > \rm 1) = \rm Q(2.5)\approx 6\cdot 10^{-3},$$
- $$\rm Pr(\it p > \rm 1) = \rm Q(3)\approx 1.3\cdot 10^{-3},$$
- $$\rm Pr(\it p < \rm 0) = \rm Q(7)\approx 10^{-12}.$$
- Der Korrelationskoeffizient $\rho = 0.8$ ist hier positiv: Hat der Prüfling im Theorieteil eher gut abgeschnitten, so ist (zumindest bei dieser Aufgabe) zu erwarten, dass auch der praktische Teil gut läuft.
- Hier ist also der Lösungsvorschlag 2 falsch. In der Praxis ist das sicher nicht immer so.
(5) Für diese Wahrscheinlichkeit gilt mit $\Delta t = \Delta p = 0.02$:
- $$\rm Pr\left [( \rm 0.5-\frac{\rm\Delta\it t}{\rm 2}\le \it t \le \rm 0.5+\frac{\rm\Delta\it t}{\rm 2})\cap(\rm 0.5-\frac{\rm\Delta\it p}{\rm 2}\le \it p \le \rm 0.5+\frac{\rm\Delta\it p}{\rm 2})\right ] \approx \rm\Delta\it t\cdot\rm\Delta\it p\cdot \it f_{tp}{\rm (}t=\rm 0.5,\hspace{0.08cm} \it p = \rm 0.5).$$
- Für die 2D-WDF gilt unter Berücksichtigung der Mittelwerte $m_t{= 0.5}$ und $m_p{= 0.7}$:
- $$f_{tp}(\it t=\rm 0.5,\hspace{0.08cm} \it p=\rm 0.5) = \rm 13.263\cdot {\rm e}^{-(-0.2)^2/0.0072}\approx 0.0513.$$
- Damit ergibt sich die gesuchte Wahrscheinlichkeit zu
- $${\rm Pr}\big[(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)\big] =0.02 \cdot 0.02 \cdot 0.0513\hspace{0.15cm}\underline{\approx 2 · 10^{-5}}.$$