Aufgaben:Aufgabe 4.12: Leistungsdichtespektrum eines Binärsignals: Unterschied zwischen den Versionen
Aus LNTwww
K (Guenter verschob die Seite Aufgabe 4.12: LDS eines Binärsignals nach Aufgabe 4.12: Leistungsdichtespektrum eines Binärsignals) |
|||
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID405__Sto_A_4_12.png|right|300px|Binäre Rechtecksignale]] | + | [[Datei:P_ID405__Sto_A_4_12.png|right|300px|frame|Binäre Rechtecksignale]] |
| − | Wir betrachten ein rechteckförmiges Binärsignal $x(t)$ mit gleichwahrscheinlichen Amplitudenwerten $+2\hspace{0.05cm}\rm V$ und $-2\hspace{0.05cm}\rm V$. Die Symboldauer beträgt $T = 1 \hspace{0.05cm}\rm | + | Wir betrachten ein rechteckförmiges Binärsignal $x(t)$ mit gleichwahrscheinlichen Amplitudenwerten $+2\hspace{0.05cm}\rm V$ und $-2\hspace{0.05cm}\rm V$. |
| − | :$$\varphi_x (\tau) = 4 \hspace{0.05cm}V^2 \cdot (1 - | \tau |/{T}).$$ | + | *Die Symboldauer beträgt $T = 1 \hspace{0.05cm}\rm µ s$. |
| + | *In [[Aufgaben:4.10_Binär_und_quaternär|Aufgabe 4.10]] wurde bereits gezeigt, dass die dazugehörige AKF auf den Bereich von $-T \le \tau\le +T$ beschränkt ist und in diesem Bereich dreieckförmig verläuft: | ||
| + | :$$\varphi_x (\tau) = 4 \hspace{0.05cm}{\rm V}^2 \cdot (1 - | \tau |/{T}).$$ | ||
| − | Hierbei ist vorausgesetzt, dass die einzelnen Symbole statistisch voneinander unabhängig sind. | + | *Hierbei ist vorausgesetzt, dass die einzelnen Symbole statistisch voneinander unabhängig sind. |
| − | Das unten skizzierte Signal $y(t)$ ist ebenfalls binär und rechteckförmig mit der gleichen Symboldauer $T = 1 \hspace{0.05cm}\rm | + | |
| + | Das unten skizzierte Signal $y(t)$ ist ebenfalls binär und rechteckförmig mit der gleichen Symboldauer $T = 1 \hspace{0.05cm}\rm µ s$. | ||
| + | *Die möglichen Amplitudenwerte sind nun aber $0\hspace{0.05cm}\rm V$ und $4\hspace{0.05cm}\rm V$. | ||
| + | * Der Amplitudenwert $4\hspace{0.05cm}\rm V$ tritt seltener auf als $0\hspace{0.05cm}\rm V$. Es gilt: | ||
:$${\rm Pr}(x(t) = 4 \hspace{0.05cm} {\rm V}) = p\hspace{0.5cm} {\rm mit}\hspace{0.5cm} 0 < p \le 0.25.$$ | :$${\rm Pr}(x(t) = 4 \hspace{0.05cm} {\rm V}) = p\hspace{0.5cm} {\rm mit}\hspace{0.5cm} 0 < p \le 0.25.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum]]. | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum]]. |
| − | + | ||
| − | *Beachten Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t= 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet: | + | *Beachten Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t= 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet: |
:$${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$ | :$${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$ | ||
| − | *Weiterhin gilt die Notation ${\rm si}(x) = \sin(x)/x$ mit folgendem Integralwert: | + | *Weiterhin gilt die Notation ${\rm si}(x) = \sin(x)/x$ mit folgendem Integralwert: |
| − | :$$\int^1_0 {\rm si}^2 ( \pi u) \, {\rm d}u \ \approx 0.456.$$ | + | :$$\int^1_0 {\rm si}^2 ( \pi \cdot u) \, {\rm d}u \ \approx 0.456.$$ |
| + | |||
| + | |||
| Zeile 25: | Zeile 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie das Leistungsdichtespektrum ${\it \Phi}_x(f)$ des bipolaren Zufallssignals $x(t)$ an. | + | {Geben Sie das Leistungsdichtespektrum ${\it \Phi}_x(f)$ des bipolaren Zufallssignals $x(t)$ an. |
| − | + | Welche LDS-Werte ergeben sich für $f= 0$, $f = 500 \hspace{0.05cm}\rm kHz$ und $f = 1 \hspace{0.05cm}\rm MHz$? | |
|type="{}"} | |type="{}"} | ||
| − | ${\it \Phi}_x(f = 0) \ = $ { 4 3% } $\ \cdot 10^{-6} \rm V^2 /Hz$ | + | ${\it \Phi}_x(f = 0) \ = \ $ { 4 3% } $\ \cdot 10^{-6} \ \rm V^2 /Hz$ |
| − | ${\it \Phi}_x(f = 500 \hspace{0. | + | ${\it \Phi}_x(f = 500 \hspace{0.08cm}\rm kHz) \ = \ $ { 1.62 3% } $\ \cdot 10^{-6} \ \rm V^2 /Hz$ |
| − | ${\it \Phi}_x(f = 1 \hspace{0. | + | ${\it \Phi}_x(f = 1 \hspace{0.08cm}\rm MHz) \ = \ $ { 0. } $\ \cdot 10^{-6} \ \rm V^2 /Hz$ |
| − | {Berechnen Sie die AKF $\varphi_y(\tau)$ des unipolaren Zufallssignals $ | + | {Berechnen Sie die AKF $\varphi_y(\tau)$ des unipolaren Zufallssignals $y(t)$. Welche AKF-Werte ergeben sich mit $p = 0.25$ für $\tau =0$, $\tau =T$ und $\tau =2T$ ? |
|type="{}"} | |type="{}"} | ||
| − | $\varphi_y(\tau = 0) \ = $ { 4 3% } $\ \rm V^2$ | + | $\varphi_y(\tau = 0) \ = \ $ { 4 3% } $\ \rm V^2$ |
| − | $\varphi_y(\tau = T) \ = $ { 1 3% } $\ \rm V^2$ | + | $\varphi_y(\tau = T) \ = \ $ { 1 3% } $\ \rm V^2$ |
| − | $\varphi_y(\tau = 2T) \ = $ { 1 3% } $\ \rm V^2$ | + | $\varphi_y(\tau = 2T) \ = \ $ { 1 3% } $\ \rm V^2$ |
| − | {Berechnen Sie das zugehörige Leistungsdichtespektrum ${\it \Phi}_y(f)$. Welcher LDS-Wert ergibt sich für $f = 500 \hspace{0.05cm}\rm kHz$? | + | {Berechnen Sie das zugehörige Leistungsdichtespektrum ${\it \Phi}_y(f)$. Welcher LDS-Wert ergibt sich für $f = 500 \hspace{0.05cm}\rm kHz$ ? |
|type="{}"} | |type="{}"} | ||
| − | ${\it \Phi}_x(f = 500 \hspace{0. | + | ${\it \Phi}_x(f = 500 \hspace{0.08cm}\rm kHz) \ = \ $ { 1.216 3% } $\ \cdot 10^{-6} \ \rm V^2 /Hz$ |
| − | {Welche mittlere Signalleistung $P_{\rm M}$ (bezogen auf den Widerstand $1 \hspace{0. | + | {Welche mittlere Signalleistung $P_{\rm M}$ $($bezogen auf den Widerstand $1 \hspace{0.08cm}\rm \Omega)$ zeigt ein Messgerät an, das nur Leistungsanteile bis $1 \hspace{0.05cm}\rm MHz$ erfasst? |
|type="{}"} | |type="{}"} | ||
| − | $P_{\rm M} \ = $ { 3.736 3% } $\ \rm V^2$ | + | $P_{\rm M} \ = \ $ { 3.736 3% } $\ \rm V^2$ |
| Zeile 55: | Zeile 69: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[Datei: P_ID406__Sto_A_4_12_a.png|right| | + | [[Datei: P_ID406__Sto_A_4_12_a.png|right|frame|Leistungsdichtespektrum mit Gleichanteil]] |
| − | '''(1)''' Das LDS ist die Fouriertransformierte der AKF. Mit der Fourierkorrespondenz auf der Angabenseite und $x_0 = 2\hspace{0.05cm}\rm V$ erhält man: | + | '''(1)''' Das LDS ist die Fouriertransformierte der AKF. |
| + | *Mit der Fourierkorrespondenz auf der Angabenseite und $x_0 = 2\hspace{0.05cm}\rm V$ erhält man: | ||
:$${\it \Phi}_x(f)= x_{\rm 0}^2 \cdot T \cdot {\rm si}^2(\pi f T).$$ | :$${\it \Phi}_x(f)= x_{\rm 0}^2 \cdot T \cdot {\rm si}^2(\pi f T).$$ | ||
| − | Die gesuchten LDS-Werte sind: | + | *Die gesuchten LDS-Werte sind: |
:$${\it \Phi}_x(f = 0)\hspace{0.15cm}\underline {=4} \cdot 10^{-6} \rm V^2 /Hz,$$ | :$${\it \Phi}_x(f = 0)\hspace{0.15cm}\underline {=4} \cdot 10^{-6} \rm V^2 /Hz,$$ | ||
:$${\it \Phi}_x(f = 500 \hspace{0.05cm}\rm kHz)\hspace{0.15cm}\underline {=1.62} \cdot 10^{-6} \rm V^2 /Hz,$$ | :$${\it \Phi}_x(f = 500 \hspace{0.05cm}\rm kHz)\hspace{0.15cm}\underline {=1.62} \cdot 10^{-6} \rm V^2 /Hz,$$ | ||
:$${\it \Phi}_x(f = 1 \hspace{0.05cm}\rm MHz)\hspace{0.15cm}\underline {=0}.$$ | :$${\it \Phi}_x(f = 1 \hspace{0.05cm}\rm MHz)\hspace{0.15cm}\underline {=0}.$$ | ||
| − | Bei $f = 1 \hspace{0.05cm}\rm MHz $ besitzt das Leistungsdichtespektrum die erste Nullstelle. | + | *Bei $f = 1 \hspace{0.05cm}\rm MHz $ besitzt das Leistungsdichtespektrum die erste Nullstelle. |
| + | |||
| − | [[Datei:P_ID407__Sto_A_4_12_b.png|right| | + | |
| − | '''(2)''' Aufgrund des rechteckigen Signalverlaufs ändert sich an der Dreiecksform der AKF prinzipiell nichts. Der AKF-Wert bei $\tau = 0$ gibt wieder das Moment | + | [[Datei:P_ID407__Sto_A_4_12_b.png|right|frame|Autokorrelationsfunktion mit Gleichanteil ]] |
| + | '''(2)''' Aufgrund des rechteckigen Signalverlaufs ändert sich an der Dreiecksform der AKF prinzipiell nichts. | ||
| + | *Der AKF-Wert bei $\tau = 0$ gibt wieder das Moment zweiter Ordnung an. | ||
| + | *Mit $p = 0.25$ erhält man: | ||
:$$\varphi_y( 0) = {1}/{4}\cdot {(\rm 4\hspace{0.05cm}V)}^2 + {3}/{4}\cdot {(\rm 0\hspace{0.05cm}V)}^2 \hspace{0.15cm}\underline{= {\rm 4\,V^2}}.$$ | :$$\varphi_y( 0) = {1}/{4}\cdot {(\rm 4\hspace{0.05cm}V)}^2 + {3}/{4}\cdot {(\rm 0\hspace{0.05cm}V)}^2 \hspace{0.15cm}\underline{= {\rm 4\,V^2}}.$$ | ||
| − | Ab $\tau =T$ ist die AKF konstant gleich $m_y^2$. Mit der Wahrscheinlichkeit $p = 0.25$ und | + | *Ab $\tau =T$ ist die AKF konstant gleich $m_y^2$. |
| − | + | *Mit der Wahrscheinlichkeit $p = 0.25$ und $m_y = p \cdot {\rm 4\hspace{0.05cm}V} + (1-p)\cdot {\rm 0\hspace{0.05cm}V} = 1 \, \rm V$ erhält man ab $\tau =T$ den konstanten Wert $\varphi_y( \tau >T) \hspace{0.15cm}\underline {=\rm 1\,V^2}$. | |
| + | |||
| − | |||
'''(3)''' Die AKF kann auch wie folgt dargestellt werden: | '''(3)''' Die AKF kann auch wie folgt dargestellt werden: | ||
:$$\varphi_y(\tau) = 1\hspace{0.05cm}{\rm V}^2 + 3\hspace{0.05cm}{\rm V}^2 \cdot \Delta (\tau).$$ | :$$\varphi_y(\tau) = 1\hspace{0.05cm}{\rm V}^2 + 3\hspace{0.05cm}{\rm V}^2 \cdot \Delta (\tau).$$ | ||
| − | *Der AKF-Gleichanteil (mit $1\hspace{0.05cm}{\rm V}^2$ | + | *Der AKF-Gleichanteil $($mit $1\hspace{0.05cm}{\rm V}^2)$ führt im LDS zu einer Diracfunktion bei $f = 0$ ⇒ siehe Skizze zur Teilaufgabe '''(1)'''. |
| − | *Der dreieckförmige AKF-Term bewirkt einen kontinuierlichen LDS-Anteil entsprechend der $\rm si^2$-Form: | + | *Der dreieckförmige AKF-Term bewirkt einen kontinuierlichen LDS-Anteil entsprechend der $\rm si^2$-Form: |
| − | :$${\it \Phi}_y(f)= 1{\rm V}^2 \cdot {\rm \delta } (f) + 3 \cdot 10^{-6} \{\rm V | + | :$${\it \Phi}_y(f)= 1{\rm V}^2 \cdot {\rm \delta } (f) + 3 \cdot 10^{-6}\ {\rm V^2\hspace{-0.1cm}/Hz} \cdot {\rm si}^2(\pi f T).$$ |
| + | |||
| + | *Für $f = 500 \hspace{0.05cm}\rm kHz$ ⇒ $f \cdot T =0.5$ ergibt sich der LDS-Wert zu ${\underline {1.216} \cdot 10^{-6} \rm V^2 /Hz}$. | ||
| + | |||
| − | |||
| − | '''(4)''' Die Leistung ist als Integral über das LDS berechenbar. Unter Berücksichtigung der spektralen Begrenzung auf $ 1 \hspace{0.05cm}\rm MHz$ erhält man mit der Substitution $u =f \cdot T$: | + | '''(4)''' Die Leistung ist als Integral über das LDS berechenbar. |
| + | *Unter Berücksichtigung der spektralen Begrenzung auf $ 1 \hspace{0.05cm}\rm MHz$ erhält man mit der Substitution $u =f \cdot T$: | ||
:$$P_{\rm M} = 1{\rm V}^2 + 3 \cdot 10^{-6} {{\rm V^2} /{\rm Hz}} \cdot \int^{\rm 1 MHz}_{-\rm 1 MHz} {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm d}f = 1{\rm V}^2 + 3 V^2 \cdot 2 \cdot \int^{1}_{\rm 0} {\rm si}^2(\pi u)\hspace{0.1cm}{\rm d}u = (1 + 3\cdot 2 \cdot 0.456)\,{\rm V^2} \hspace{0.15cm}\underline{= 3.736 \, {\rm V^2}}. $$ | :$$P_{\rm M} = 1{\rm V}^2 + 3 \cdot 10^{-6} {{\rm V^2} /{\rm Hz}} \cdot \int^{\rm 1 MHz}_{-\rm 1 MHz} {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm d}f = 1{\rm V}^2 + 3 V^2 \cdot 2 \cdot \int^{1}_{\rm 0} {\rm si}^2(\pi u)\hspace{0.1cm}{\rm d}u = (1 + 3\cdot 2 \cdot 0.456)\,{\rm V^2} \hspace{0.15cm}\underline{= 3.736 \, {\rm V^2}}. $$ | ||
| − | Würden dagegen alle Spektralanteile erfasst, ergäbe sich die mittlere Leistung zu $\varphi_y( \tau= 0) = 4 \, {\rm V^2}$. | + | *Würden dagegen alle Spektralanteile erfasst, ergäbe sich die mittlere Leistung zu $\varphi_y( \tau= 0) = 4 \, {\rm V^2}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 16. März 2022, 16:56 Uhr
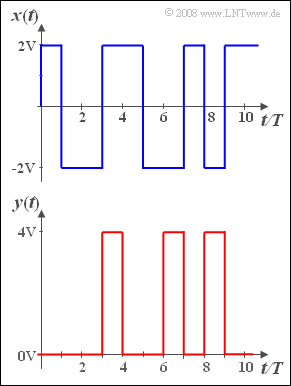
Wir betrachten ein rechteckförmiges Binärsignal $x(t)$ mit gleichwahrscheinlichen Amplitudenwerten $+2\hspace{0.05cm}\rm V$ und $-2\hspace{0.05cm}\rm V$.
- Die Symboldauer beträgt $T = 1 \hspace{0.05cm}\rm µ s$.
- In Aufgabe 4.10 wurde bereits gezeigt, dass die dazugehörige AKF auf den Bereich von $-T \le \tau\le +T$ beschränkt ist und in diesem Bereich dreieckförmig verläuft:
- $$\varphi_x (\tau) = 4 \hspace{0.05cm}{\rm V}^2 \cdot (1 - | \tau |/{T}).$$
- Hierbei ist vorausgesetzt, dass die einzelnen Symbole statistisch voneinander unabhängig sind.
Das unten skizzierte Signal $y(t)$ ist ebenfalls binär und rechteckförmig mit der gleichen Symboldauer $T = 1 \hspace{0.05cm}\rm µ s$.
- Die möglichen Amplitudenwerte sind nun aber $0\hspace{0.05cm}\rm V$ und $4\hspace{0.05cm}\rm V$.
- Der Amplitudenwert $4\hspace{0.05cm}\rm V$ tritt seltener auf als $0\hspace{0.05cm}\rm V$. Es gilt:
- $${\rm Pr}(x(t) = 4 \hspace{0.05cm} {\rm V}) = p\hspace{0.5cm} {\rm mit}\hspace{0.5cm} 0 < p \le 0.25.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Leistungsdichtespektrum.
- Beachten Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t= 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet:
- $${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$
- Weiterhin gilt die Notation ${\rm si}(x) = \sin(x)/x$ mit folgendem Integralwert:
- $$\int^1_0 {\rm si}^2 ( \pi \cdot u) \, {\rm d}u \ \approx 0.456.$$
Fragebogen
Musterlösung
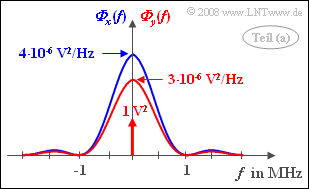
(1) Das LDS ist die Fouriertransformierte der AKF.
- Mit der Fourierkorrespondenz auf der Angabenseite und $x_0 = 2\hspace{0.05cm}\rm V$ erhält man:
- $${\it \Phi}_x(f)= x_{\rm 0}^2 \cdot T \cdot {\rm si}^2(\pi f T).$$
- Die gesuchten LDS-Werte sind:
- $${\it \Phi}_x(f = 0)\hspace{0.15cm}\underline {=4} \cdot 10^{-6} \rm V^2 /Hz,$$
- $${\it \Phi}_x(f = 500 \hspace{0.05cm}\rm kHz)\hspace{0.15cm}\underline {=1.62} \cdot 10^{-6} \rm V^2 /Hz,$$
- $${\it \Phi}_x(f = 1 \hspace{0.05cm}\rm MHz)\hspace{0.15cm}\underline {=0}.$$
- Bei $f = 1 \hspace{0.05cm}\rm MHz $ besitzt das Leistungsdichtespektrum die erste Nullstelle.
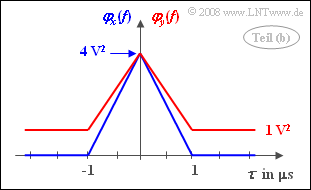
(2) Aufgrund des rechteckigen Signalverlaufs ändert sich an der Dreiecksform der AKF prinzipiell nichts.
- Der AKF-Wert bei $\tau = 0$ gibt wieder das Moment zweiter Ordnung an.
- Mit $p = 0.25$ erhält man:
- $$\varphi_y( 0) = {1}/{4}\cdot {(\rm 4\hspace{0.05cm}V)}^2 + {3}/{4}\cdot {(\rm 0\hspace{0.05cm}V)}^2 \hspace{0.15cm}\underline{= {\rm 4\,V^2}}.$$
- Ab $\tau =T$ ist die AKF konstant gleich $m_y^2$.
- Mit der Wahrscheinlichkeit $p = 0.25$ und $m_y = p \cdot {\rm 4\hspace{0.05cm}V} + (1-p)\cdot {\rm 0\hspace{0.05cm}V} = 1 \, \rm V$ erhält man ab $\tau =T$ den konstanten Wert $\varphi_y( \tau >T) \hspace{0.15cm}\underline {=\rm 1\,V^2}$.
(3) Die AKF kann auch wie folgt dargestellt werden:
- $$\varphi_y(\tau) = 1\hspace{0.05cm}{\rm V}^2 + 3\hspace{0.05cm}{\rm V}^2 \cdot \Delta (\tau).$$
- Der AKF-Gleichanteil $($mit $1\hspace{0.05cm}{\rm V}^2)$ führt im LDS zu einer Diracfunktion bei $f = 0$ ⇒ siehe Skizze zur Teilaufgabe (1).
- Der dreieckförmige AKF-Term bewirkt einen kontinuierlichen LDS-Anteil entsprechend der $\rm si^2$-Form:
- $${\it \Phi}_y(f)= 1{\rm V}^2 \cdot {\rm \delta } (f) + 3 \cdot 10^{-6}\ {\rm V^2\hspace{-0.1cm}/Hz} \cdot {\rm si}^2(\pi f T).$$
- Für $f = 500 \hspace{0.05cm}\rm kHz$ ⇒ $f \cdot T =0.5$ ergibt sich der LDS-Wert zu ${\underline {1.216} \cdot 10^{-6} \rm V^2 /Hz}$.
(4) Die Leistung ist als Integral über das LDS berechenbar.
- Unter Berücksichtigung der spektralen Begrenzung auf $ 1 \hspace{0.05cm}\rm MHz$ erhält man mit der Substitution $u =f \cdot T$:
- $$P_{\rm M} = 1{\rm V}^2 + 3 \cdot 10^{-6} {{\rm V^2} /{\rm Hz}} \cdot \int^{\rm 1 MHz}_{-\rm 1 MHz} {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm d}f = 1{\rm V}^2 + 3 V^2 \cdot 2 \cdot \int^{1}_{\rm 0} {\rm si}^2(\pi u)\hspace{0.1cm}{\rm d}u = (1 + 3\cdot 2 \cdot 0.456)\,{\rm V^2} \hspace{0.15cm}\underline{= 3.736 \, {\rm V^2}}. $$
- Würden dagegen alle Spektralanteile erfasst, ergäbe sich die mittlere Leistung zu $\varphi_y( \tau= 0) = 4 \, {\rm V^2}$.