Stochastische Signaltheorie/Leistungsdichtespektrum (LDS): Unterschied zwischen den Versionen
| (18 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Theorem von Wiener-Chintchine== | ==Theorem von Wiener-Chintchine== | ||
| − | Im Weiteren beschränken wir uns auf ergodische Prozesse. Wie im [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Ergodische_Zufallsprozesse|letzten Kapitel]] gezeigt wurde, gelten dann die folgenden Aussagen: | + | <br> |
| − | *Jede einzelne Musterfunktion $x_i(t)$ ist repräsentativ für den gesamten Zufallsprozess $\{x_i(t)\}$. Alle Zeitmittelwerte sind somit identisch mit den dazugehörigen Scharmittelwerten. | + | Im Weiteren beschränken wir uns auf ergodische Prozesse. Wie im [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Ergodische_Zufallsprozesse|letzten Kapitel]] gezeigt wurde, gelten dann die folgenden Aussagen: |
| − | *Die Autokorrelationsfunktion, die allgemein von den beiden Zeitparametern $t_1$ und $t_2$ beeinflusst wird, hängt nur noch von der Zeitdifferenz $τ = t_2 – t_1$ ab: | + | *Jede einzelne Musterfunktion $x_i(t)$ ist repräsentativ für den gesamten Zufallsprozess $\{x_i(t)\}$. |
| − | $$\varphi_x(t_1,t_2)={\rm E}[x(t_{\rm 1})\cdot x(t_{\rm 2})] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$ | + | *Alle Zeitmittelwerte sind somit identisch mit den dazugehörigen Scharmittelwerten. |
| + | *Die Autokorrelationsfunktion, die allgemein von den beiden Zeitparametern $t_1$ und $t_2$ beeinflusst wird, hängt nur noch von der Zeitdifferenz $τ = t_2 – t_1$ ab: | ||
| + | :$$\varphi_x(t_1,t_2)={\rm E}\big[x(t_{\rm 1})\cdot x(t_{\rm 2})\big] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$ | ||
| − | + | Die Autokorrelationsfunktion liefert quantitative Aussagen über die (linearen) statistischen Bindungen innerhalb des ergodischen Prozesses $\{x_i(t)\}$ im Zeitbereich. Die äquivalente Beschreibungsgröße im Frequenzbereich ist die „spektrale Leistungsdichte”, häufig auch als „Leistungsdichtespektrum” bezeichnet. | |
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| − | $${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\pi} f \tau} {\rm d} \tau. $$ | + | $\text{Definition:}$ Das '''Leistungsdichtespektrum''' $\rm (LDS)$ eines ergodischen Zufallsprozesses $\{x_i(t)\}$ ist die Fouriertransformierte der Autokorrelationsfunktion $\rm (AKF)$: |
| − | Diesen Funktionalzusammenhang nennt man das Theorem von [https://de.wikipedia.org/wiki/Norbert_Wiener Wiener] und [https://de.wikipedia.org/wiki/Alexander_Jakowlewitsch_Chintschin | + | :$${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} \tau. $$ |
| − | + | Diesen Funktionalzusammenhang nennt man das "Theorem von [https://de.wikipedia.org/wiki/Norbert_Wiener Wiener] und [https://de.wikipedia.org/wiki/Alexander_Jakowlewitsch_Chintschin Chintchin]". }} | |
| − | Ebenso kann die | + | Ebenso kann die Autokorrelationsfunktion als Fourierrücktransformierte des Leistungsdichtespektrums berechnet werden (siehe Seite [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_zweite_Fourierintegral|"Fourierrücktransformation"]]): |
| − | :$$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x \cdot {\rm e}^{{\rm j\pi} f \tau} {\rm d} f.$$ | + | :$$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} f.$$ |
| − | Die beiden Gleichungen sind nur dann direkt anwendbar, wenn der Zufallsprozess weder einen Gleichanteil noch periodische Anteile beinhaltet. Andernfalls muss man nach den Angaben entsprechend der Seite [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)#Leistungsdichtespektrum_mit_Gleichsignalkomponente|Spektrale Leistungsdichte mit Gleichsignalkomponente]] vorgehen. | + | *Die beiden Gleichungen sind nur dann direkt anwendbar, wenn der Zufallsprozess weder einen Gleichanteil noch periodische Anteile beinhaltet. |
| + | *Andernfalls muss man nach den Angaben entsprechend der Seite [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)#Leistungsdichtespektrum_mit_Gleichsignalkomponente|"Spektrale Leistungsdichte mit Gleichsignalkomponente"]] vorgehen. | ||
==Physikalische Interpretation und Messung== | ==Physikalische Interpretation und Messung== | ||
| − | Das folgende Bild zeigt eine Anordnung zur (näherungsweisen) messtechnischen Bestimmung des Leistungsdichtespektrums ${\it \Phi}_x(f)$. | + | <br> |
| + | Das folgende Bild zeigt eine Anordnung zur (näherungsweisen) messtechnischen Bestimmung des Leistungsdichtespektrums ${\it \Phi}_x(f)$. Hierzu ist anzumerken: | ||
| + | *Das Zufallssignal $x(t)$ wird auf ein (möglichst) rechteckförmiges und (möglichst) schmalbandiges Filter mit Mittenfrequenz $f$ und Bandbreite $Δf$ gegeben, wobei $Δf$ entsprechend der gewünschten Frequenzauflösung hinreichend klein gewählt werden muss. | ||
| + | *Das entsprechende Ausgangssignal $x_f(t)$ wird quadriert und anschließend der Mittelwert über eine hinreichend lange Messdauer $T_{\rm M}$ gebildet. Damit erhält man die "Leistung von $x_f(t)$" bzw. die "Leistungsanteile von $x(t)$ im Spektralbereich von $f - Δf/2$ bis $f + Δf/2$": | ||
| + | [[Datei: P_ID387__Sto_T_4_5_S2_neu.png |right|frame| Zur Messung des Leistungsdichtespektrums]] | ||
| + | :$$P_{x_f} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm}\rm d \it t.$$ | ||
| + | *Die Division durch $Δf$ führt zur spektralen Leistungsdichte: | ||
| + | :$${{\it \Phi}_{x \rm +}}(f) =\frac{P_{x_f}}{{\rm \Delta} f} \hspace {0.5cm} {\rm bzw.} \hspace {0.5cm} {\it \Phi}_{x}(f) = \frac{P_{x_f}}{{\rm 2 \cdot \Delta} f}.$$ | ||
| + | *Hierbei bezeichnet ${\it \Phi}_{x+}(f) = 2 · {\it \Phi}_x(f)$ das einseitig definierte LDS (nur positive Frequenzen). Für $f<0$ ⇒ ${\it \Phi}_{x+}(f) = 0$. | ||
| + | *Üblicherweise wird das zweiseitige Leistungsdichtespektrum verwendet. Für dieses gilt: | ||
| + | :$${\it \Phi}_x(–f) = {\it \Phi}_x(f).$$ | ||
| + | *Während die Leistung $P_{x_f}$ mit kleiner werdender Bandbreite $Δf$ gegen Null tendiert, bleibt die spektrale Leistungsdichte ab einem hinreichend kleinen Wert von $Δf$ nahezu konstant. Für die exakte Bestimmung von ${\it \Phi}_x(f)$ sind zwei Grenzübergänge notwendig: | ||
| + | :$${{\it \Phi}_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$ | ||
| − | [[Datei: | + | {{BlaueBox|TEXT= |
| + | $\text{Fazit:}$ | ||
| + | *Aus dieser physikalischen Interpretation folgt weiter, dass das Leistungsdichtespektrum stets reell ist und nie negativ werden kann. | ||
| + | *Die gesamte Signalleistung von $x(t)$ erhält man dann durch Integration über alle Spektralanteile: | ||
| + | :$$P_x = \int^{\infty}_{0}{\it \Phi}_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}{\it \Phi}_x(f)\hspace{0.1cm} {\rm d} f .$$}} | ||
| + | |||
| + | ==Reziprozitätsgesetz von AKF-Zeitdauer und LDS-Bandbreite== | ||
| + | <br> | ||
| + | Alle im Buch „Signaldarstellung” für deterministische Signale hergeleiteten [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation|Gesetzmäßigkeiten der Fouriertransformation]] können auch auf die | ||
| + | [[Datei:P_ID390__Sto_T_4_5_S3_Ganz_neu.png |right|frame| Zum Reziprozitätsgesetz von AKF und LDS]] | ||
| + | *Autokorrelationsfunktion $\rm (AKF)$ und | ||
| + | *das Leistungsdichtespektrum $\rm (LDS)$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | eines Zufallsprozesses angewendet werden. Aufgrund der spezifischen Eigenschaften | |
| − | + | *von Autokorrelationsfunktion (stets reell und gerade) | |
| + | *und Leistungsdichtespektrum (stets reell, gerade und nicht–negativ) | ||
| − | |||
| − | |||
| − | + | liefern allerdings nicht alle Gesetze sinnvolle Ergebnisse. | |
| − | Wir betrachten nun wie im Abschnitt [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Interpretation_der_Autokorrelationsfunktion|Interpretation der Autokorrelationsfunktion]] zwei unterschiedliche ergodische Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ | + | Wir betrachten nun wie im Abschnitt [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Interpretation_der_Autokorrelationsfunktion|"Interpretation der Autokorrelationsfunktion"]] zwei unterschiedliche ergodische Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ anhand |
| − | *der beiden Mustersignale $x(t)$ | + | *der beiden Mustersignale $x(t)$ und $y(t)$ ⇒ obere Skizze, |
| − | *der beiden Autokorrelationsfunktionen $φ_x(τ)$ | + | *der beiden Autokorrelationsfunktionen $φ_x(τ)$ und $φ_y(τ)$ ⇒ mittlere Skizze, |
| − | *der beiden Leistungsdichtespektren ${\it \Phi}_x(f)$ | + | *der beiden Leistungsdichtespektren ${\it \Phi}_x(f)$ und ${\it \Phi}_y(f)$ ⇒ untere Skizze. |
| − | Anhand dieser Grafiken sind folgende Aussagen möglich: | + | Anhand dieser beispielhaften Grafiken sind folgende Aussagen möglich: |
| − | *Die Flächen unter den LDS-Kurven sind gleich ⇒ die Prozesse besitzen gleiche Leistung: | + | *Die Flächen unter den LDS-Kurven sind gleich ⇒ die Prozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ besitzen hier gleiche Leistung: |
:$${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$ | :$${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$ | ||
| − | *Das aus der klassischen (deterministischen) Systemtheorie bekannte Reziprozitätsgesetz von Zeitdauer und Bandbreite gilt hier ebenfalls: Eine schmale Autokorrelationsfunktion entspricht einem breiten Leistungsdichtespektrum und umgekehrt. | + | |
| − | *Als Beschreibungsgröße verwenden wir hier die äquivalente LDS-Bandbreite $∇f$ (man spricht | + | *Das aus der klassischen (deterministischen) Systemtheorie bekannte [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Reziprozit.C3.A4tsgesetz_von_Zeitdauer_und_Bandbreite|"Reziprozitätsgesetz von Zeitdauer und Bandbreite"]] gilt hier ebenfalls: '''Eine schmale Autokorrelationsfunktion entspricht einem breiten Leistungsdichtespektrum und umgekehrt'''. |
| + | |||
| + | *Als Beschreibungsgröße verwenden wir hier die '''äquivalente LDS-Bandbreite''' $∇f$ $($man spricht„Nabla-f”$)$, ähnlich definiert wie die äquivalente AKF-Dauer $∇τ$ im Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Interpretation_der_Autokorrelationsfunktion|"Interpretation der Autokorrelationsfunktion"]]: | ||
:$${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, \hspace{0.5cm}{ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$ | :$${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, \hspace{0.5cm}{ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$ | ||
| + | |||
*Mit diesen Definitionen gilt der folgende grundlegende Zusammenhang: | *Mit diesen Definitionen gilt der folgende grundlegende Zusammenhang: | ||
:$${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm bzw.}\hspace{1cm} | :$${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm bzw.}\hspace{1cm} | ||
{{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$ | {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$ | ||
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| − | *Die Kenngrößen des höherfrequenten Signals $x(t)$ sind $∇τ_x = 0.33\hspace{0. | + | $\text{Beispiel 1:}$ Wir gehen von der oberen Grafik auf dieser Seite aus: |
| − | *Die äquivalente AKF-Dauer des Signals $y(t)$ ist dreimal so groß: $∇τ_y = 1 \hspace{0. | + | *Die Kenngrößen des höherfrequenten Signals $x(t)$ sind $∇τ_x = 0.33\hspace{0.08cm} \rm µs$ und $∇f_x = 3 \hspace{0.08cm} \rm MHz$. |
| − | * | + | *Die äquivalente AKF-Dauer des Signals $y(t)$ ist dreimal so groß: $∇τ_y = 1 \hspace{0.08cm} \rm µs$. |
| + | *Dessen äquivalente LDS-Bandbreite beträgt somit nur mehr $∇f_y = ∇f_x/3 = 1 \hspace{0.08cm} \rm MHz$. }} | ||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Allgemein gilt:}$ | ||
| + | '''Das Produkt aus äquivalenter AKF-Dauer ${ {\rm \nabla} \tau_x}$ und äquivalenter LDS-Bandbreite $ { {\rm \nabla} f_x}$ ist immer gleich $1$''': | ||
| + | :$${ {\rm \nabla} \tau_x} \cdot { {\rm \nabla} f_x} = 1.$$}} | ||
| − | |||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| − | :$${{\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac {{\it \Phi}_x(f = {\rm 0)}}{ \varphi_x(\tau = \rm 0)},$$ | + | $\text{Beweis:}$ Entsprechend den obigen Definitionen gilt: |
| − | :$${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)}}{{\it \Phi}_x(f = \rm 0)}.$$ | + | :$${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac { {\it \Phi}_x(f = {\rm 0)} }{ \varphi_x(\tau = \rm 0)},$$ |
| + | :$${ {\rm \nabla} f_x} = \frac {1}{ {\it \Phi}_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{ {\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)} }{ {\it \Phi}_x(f = \rm 0)}.$$ | ||
| − | + | Das Produkt ist somit gleich $1$. | |
| + | <div align="right">'''q.e.d.'''</div> }} | ||
| − | Ein Grenzfall des Reziprozitätsgesetzes stellt das so genannte '''Weiße Rauschen''' dar: | + | {{GraueBox|TEXT= |
| − | *Dieses beinhaltet alle Spektralanteile (bis ins Unendliche). | + | $\text{Beispiel 2:}$ |
| − | *Die äquivalente LDS-Bandbreite $∇f$ | + | Ein Grenzfall des Reziprozitätsgesetzes stellt das so genannte '''Weiße Rauschen''' dar: |
| − | + | *Dieses beinhaltet alle Spektralanteile (bis ins Unendliche). | |
| + | *Die äquivalente LDS-Bandbreite $∇f$ ist also unendlich groß. | ||
| − | |||
| + | Das hier angegebene Gesetz besagt, dass damit für die äquivalente AKF-Dauer $∇τ = 0$ gelten muss ⇒ '''Weißes Rauschen besitzt stets eine diracförmige AKF'''. | ||
| − | + | Mehr zu dieser Thematik finden Sie im dreiteiligen Lernvideo [[Der_AWGN-Kanal_(Lernvideo)|"Der AWGN-Kanal"]], insbesondere im zweiten Teil.}} | |
| − | |||
| − | |||
| − | |||
| − | Wir | + | ==Leistungsdichtespektrum mit Gleichsignalkomponente== |
| − | $ | + | <br> |
| + | Wir gehen von einem gleichsignalfreien Zufallsprozess $\{x_i(t)\}$ aus. Weiter setzen wir voraus, dass der Prozess auch keine periodischen Anteile beinhaltet. Dann gilt: | ||
| + | *Die Autokorrelationsfunktion $φ_x(τ)$ verschwindet für $τ → ∞$. | ||
| + | *Das Leistungsdichtespektrum ${\it \Phi}_x(f)$ – berechenbar als die Fouriertransformierte von $φ_x(τ)$ – ist sowohl wert– als auch zeitkontinuierlich, also ohne diskrete Anteile. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Wir betrachten nun einen zweiten Zufallsprozess $\{y_i(t)\}$, der sich vom Prozess $\{x_i(t)\}$ lediglich durch eine zusätzliche Gleichsignalkomponente $m_y$ unterscheidet: | ||
| + | :$$\left\{ y_i (t) \right\} = \left\{ x_i (t) + m_y \right\}.$$ | ||
| − | + | Die statistischen Beschreibungsgrößen des mittelwertbehafteten Zufallsprozesses $\{y_i(t)\}$ weisen dann folgende Eigenschaften auf: | |
| + | *Der Grenzwert der AKF für $τ → ∞$ ist nun nicht mehr Null, sondern $m_y^2$. Im gesamten $τ$–Bereich von $–∞$ bis $+∞$ ist die AKF $φ_y(τ)$ um $m_y^2$ größer als $φ_x(τ)$: | ||
| + | :$${\varphi_y ( \tau)} = {\varphi_x ( \tau)} + m_y^2 . $$ | ||
| + | *Nach den elementaren Gesetzen der Fouriertransformation führt der konstante AKF-Beitrag im LDS zu einer Diracfunktion $δ(f)$ mit dem Gewicht $m_y^2$: | ||
| + | :$${{\it \Phi}_y ( f)} = {\Phi_x ( f)} + m_y^2 \cdot \delta (f). $$ | ||
| − | Herleitung und Visualisierung der Diracfunktion | + | *Nähere Informationen zur Diracfunktion finden Sie im Kapitel [[Signaldarstellung/Allgemeine_Beschreibung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals|"Gleichsignal - Grenzfall eines periodischen Signals"]] des Buches „Signaldarstellung”. Zudem möchten wir Sie hier auf das Lernvideo [[Herleitung_und_Visualisierung_der_Diracfunktion_(Lernvideo)|"Herleitung und Visualisierung der Diracfunktion"]] hinweisen. |
==Numerische LDS-Ermittlung== | ==Numerische LDS-Ermittlung== | ||
| − | Autokorrelationsfunktion und Leistungsdichtespektrum sind über die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Fouriertransformation|Fouriertransformation]] streng miteinander verknüpft. Dieser Zusammenhang gilt auch bei zeitdiskreter AKF-Darstellung, also für | + | <br> |
| − | $${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$ | + | Autokorrelationsfunktion und Leistungsdichtespektrum sind über die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Fouriertransformation|Fouriertransformation]] streng miteinander verknüpft. Dieser Zusammenhang gilt auch bei zeitdiskreter AKF-Darstellung mit dem Abtastoperator ${\rm A} \{ \varphi_x ( \tau ) \} $, also für |
| + | :$${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$ | ||
| − | Der Übergang vom Zeit | + | Der Übergang vom Zeit– in den Spektralbereich kann mit folgenden Schritten hergeleitet werden: |
| − | *Der Abstand $T_{\rm A}$ zweier Abtastwerte ist durch die absolute Bandbreite $B_x$ (maximal auftretende Frequenz innerhalb des Prozesses) über das Abtasttheorem festgelegt: | + | *Der Abstand $T_{\rm A}$ zweier Abtastwerte ist durch die absolute Bandbreite $B_x$ $($maximal auftretende Frequenz innerhalb des Prozesses$)$ über das Abtasttheorem festgelegt: |
| − | $$T_{\rm A}\le\frac{1}{2B_x}.$$ | + | :$$T_{\rm A}\le\frac{1}{2B_x}.$$ |
| − | *Die Fouriertransformierte der zeitdiskreten | + | *Die Fouriertransformierte der zeitdiskreten $($abgetasteten$)$ Autokorrelationsfunktion ergibt ein mit ${\rm 1}/T_{\rm A}$ periodisches Leistungsdichtespektrum: |
| − | $${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\ | + | :$${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{{\it \Phi}_x} ( f) \} = \sum_{\mu = - \infty}^{\infty} {{\it \Phi}_x} ( f - \frac {\mu}{T_{\rm A}}).$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ Da sowohl $φ_x(τ)$ als auch ${\it \Phi}_x(f)$ gerade und reelle Funktionen sind, gilt der Zusammenhang: | ||
| + | :$${\rm P} \{ { {\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{\infty} \varphi_x ( k T_{\rm A}) \cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$ | ||
| + | *Das Leistungsdichtespektrum (LDS) des zeitkontinuierlichen Prozesses erhält man aus ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ durch Bandbegrenzung auf den Bereich $\vert f \vert ≤ 1/(2T_{\rm A})$. | ||
| + | *Im Zeitbereich bedeutet diese Operation eine Interpolation der einzelnen AKF-Abtastwerte mit der ${\rm si}$–Funktion, wobei ${\rm si}(x)$ für $\sin(x)/x$ steht. }} | ||
| − | |||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 3:}$ Eine gaußförmige AKF $φ_x(τ)$ wird im Abstand $T_{\rm A}$ abgetastet, wobei das Abtasttheorem erfüllt ist: | ||
| + | [[Datei:P_ID425__Sto_T_4_5_S5_neu.png |right|frame| Zeitdiskrete Autokorrelationsfunktion, periodisch fortgesetztes Leistungsdichtespektrum]] | ||
| + | *Die Fouriertransformierte der zeitdiskreten Autokorrelationsfunktion ${\rm A} \{φ_x(τ) \}$ sei ${\rm P} \{ { {\it \Phi}_x} ( f) \}$. | ||
| − | + | ||
| + | *Diese mit ${\rm 1}/T_{\rm A}$ periodische Funktion ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ ist dementsprechend unendlich weit ausgedehnt (roter Kurvenzug). | ||
| + | |||
| + | *Das Leistungsdichtespektrum ${\it \Phi}_x(f)$ des zeitkontinuierlichen Prozesses $\{x_i(t)\}$ erhält man durch Bandbegrenzung auf den im Bild blau hinterlegten Frequenzbereich $\vert f · T_{\rm A} \vert ≤ 0.5$. }} | ||
| − | + | ==Genauigkeit der numerischen LDS-Berechnung== | |
| − | {{ | + | <br> |
| + | Für die nachfolgende Analyse gehen wir von folgenden Annahmen aus: | ||
| + | #Die zeitdiskrete AKF $φ_x(k · T_{\rm A})$ wurde aus $N$ Abtastwerten numerisch ermittelt. | ||
| + | #Wie auf der Seite [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Genauigkeit_der_numerischen_AKF-Berechnung|"Genauigkeit der numerischen AKF-Berechnung"]] gezeigt, sind diese Werte fehlerhaft und die Fehler korreliert, wenn $N$ zu klein gewählt wurde. | ||
| + | #Zur Berechnung des periodischen Leistungsdichtespektrums $\rm (LDS)$ verwenden wir nur die AKF-Werte $φ_x(0)$, ... , $φ_x(K · T_{\rm A})$: | ||
| + | ::$${\rm P} \{{{\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{K} \varphi_x ( k T_{\rm A})\cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$ | ||
| − | = | + | {{BlaueBox|TEXT= |
| − | + | $\text{Fazit:}$ | |
| − | * | + | Die Genauigkeit der LDS-Berechnung wird im starken Maße durch den Parameter $K$ bestimmt: |
| − | + | *Ist $K$ zu klein gewählt, so werden die eigentlich vorhandenen AKF-Werte $φ_x(k · T_{\rm A})$ mit $k > K$ nicht berücksichtigt. | |
| − | + | *Bei zu großem $K$ werden auch solche AKF-Werte berücksichtigt, die eigentlich Null sein sollten und nur wegen der numerischen AKF-Berechnung endlich sind. | |
| + | *Diese Werte sind allerdings – bedingt durch ein zu kleines $N$ bei der AKF–Ermittlung – nur Fehler, und beinträchtigen die LDS-Berechnung mehr als dass sie einen brauchbaren Beitrag zum Ergebnis liefern. }} | ||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel 4:}$ Wir betrachten hier einen mittelwertfreien Prozess mit statistisch unabhängigen Abtastwerten. Deshalb sollte eigentlich nur der AKF–Wert $φ_x(0) = σ_x^2$ von Null verschieden sein. | |
| − | + | [[Datei:P_ID643__Sto_T_4_5_S5_b.png |450px|right|frame| Genauigkeit der numerischen LDS-Berechnung]] | |
| − | |||
| + | *Ermittelt man aber die AKF numerisch aus lediglich $N = 1000$ Abtastwerten, so erhält man auch für $k ≠ 0$ endliche AKF–Werte. | ||
| − | + | *Das obere Bild zeigt, dass diese fehlerhaften AKF–Werte bis zu $6\%$ des Maximalwertes betragen können. | |
| + | |||
| + | *Unten ist das numerisch ermittelte LDS dargestellt. Der theoretische Verlauf (gelbe Kurve) sollte für $\vert f · T_{\rm A} \vert ≤ 0.5$ konstant sein. | ||
| + | |||
| + | *Die grüne und die violette Kurve verdeutlichen, wie durch $K = 3$ bzw. $K = 10$ das Ergebnis gegenüber $K = 0$ verfälscht wird. | ||
| − | |||
| − | + | Im betrachteten Fall (statistisch unabhängige Zufallsgrößen) wächst der Fehler monoton mit steigendem $K$. Bei einer Zufallsgröße mit statistischen Bindungen gibt es dagegen jeweils einen optimalen Wert für $K$. | |
| − | + | #Wird dieser zu klein gewählt, so werden signifikante Bindungen nicht berücksichtigt. | |
| + | #Ein zu großer Wert führt dagegen zu Oszillationen, die vorwiegend auf fehlerhafte AKF–Werte zurückzuführen sind.}} | ||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:Aufgabe_4.12:_Leistungsdichtespektrum_eines_Binärsignals|Aufgabe 4.12: Leistungsdichtespektrum eines Binärsignals]] | ||
| − | [[ | + | [[Aufgaben:4.12Z Weißes Rauschen|Aufgabe 4.12Z: Weißes Rauschen]] |
| + | [[Aufgaben:4.13 Gaußförmige AKF|Aufgabe 4.13: Gaußförmige AKF]] | ||
| − | + | [[Aufgaben:4.13Z AMI-Code|Aufgabe 4.13Z: AMI-Code]] | |
| − | |||
| − | |||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 16. März 2022, 16:59 Uhr
Inhaltsverzeichnis
Theorem von Wiener-Chintchine
Im Weiteren beschränken wir uns auf ergodische Prozesse. Wie im letzten Kapitel gezeigt wurde, gelten dann die folgenden Aussagen:
- Jede einzelne Musterfunktion $x_i(t)$ ist repräsentativ für den gesamten Zufallsprozess $\{x_i(t)\}$.
- Alle Zeitmittelwerte sind somit identisch mit den dazugehörigen Scharmittelwerten.
- Die Autokorrelationsfunktion, die allgemein von den beiden Zeitparametern $t_1$ und $t_2$ beeinflusst wird, hängt nur noch von der Zeitdifferenz $τ = t_2 – t_1$ ab:
- $$\varphi_x(t_1,t_2)={\rm E}\big[x(t_{\rm 1})\cdot x(t_{\rm 2})\big] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$
Die Autokorrelationsfunktion liefert quantitative Aussagen über die (linearen) statistischen Bindungen innerhalb des ergodischen Prozesses $\{x_i(t)\}$ im Zeitbereich. Die äquivalente Beschreibungsgröße im Frequenzbereich ist die „spektrale Leistungsdichte”, häufig auch als „Leistungsdichtespektrum” bezeichnet.
$\text{Definition:}$ Das Leistungsdichtespektrum $\rm (LDS)$ eines ergodischen Zufallsprozesses $\{x_i(t)\}$ ist die Fouriertransformierte der Autokorrelationsfunktion $\rm (AKF)$:
- $${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} \tau. $$
Diesen Funktionalzusammenhang nennt man das "Theorem von Wiener und Chintchin".
Ebenso kann die Autokorrelationsfunktion als Fourierrücktransformierte des Leistungsdichtespektrums berechnet werden (siehe Seite "Fourierrücktransformation"):
- $$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} f.$$
- Die beiden Gleichungen sind nur dann direkt anwendbar, wenn der Zufallsprozess weder einen Gleichanteil noch periodische Anteile beinhaltet.
- Andernfalls muss man nach den Angaben entsprechend der Seite "Spektrale Leistungsdichte mit Gleichsignalkomponente" vorgehen.
Physikalische Interpretation und Messung
Das folgende Bild zeigt eine Anordnung zur (näherungsweisen) messtechnischen Bestimmung des Leistungsdichtespektrums ${\it \Phi}_x(f)$. Hierzu ist anzumerken:
- Das Zufallssignal $x(t)$ wird auf ein (möglichst) rechteckförmiges und (möglichst) schmalbandiges Filter mit Mittenfrequenz $f$ und Bandbreite $Δf$ gegeben, wobei $Δf$ entsprechend der gewünschten Frequenzauflösung hinreichend klein gewählt werden muss.
- Das entsprechende Ausgangssignal $x_f(t)$ wird quadriert und anschließend der Mittelwert über eine hinreichend lange Messdauer $T_{\rm M}$ gebildet. Damit erhält man die "Leistung von $x_f(t)$" bzw. die "Leistungsanteile von $x(t)$ im Spektralbereich von $f - Δf/2$ bis $f + Δf/2$":
- $$P_{x_f} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm}\rm d \it t.$$
- Die Division durch $Δf$ führt zur spektralen Leistungsdichte:
- $${{\it \Phi}_{x \rm +}}(f) =\frac{P_{x_f}}{{\rm \Delta} f} \hspace {0.5cm} {\rm bzw.} \hspace {0.5cm} {\it \Phi}_{x}(f) = \frac{P_{x_f}}{{\rm 2 \cdot \Delta} f}.$$
- Hierbei bezeichnet ${\it \Phi}_{x+}(f) = 2 · {\it \Phi}_x(f)$ das einseitig definierte LDS (nur positive Frequenzen). Für $f<0$ ⇒ ${\it \Phi}_{x+}(f) = 0$.
- Üblicherweise wird das zweiseitige Leistungsdichtespektrum verwendet. Für dieses gilt:
- $${\it \Phi}_x(–f) = {\it \Phi}_x(f).$$
- Während die Leistung $P_{x_f}$ mit kleiner werdender Bandbreite $Δf$ gegen Null tendiert, bleibt die spektrale Leistungsdichte ab einem hinreichend kleinen Wert von $Δf$ nahezu konstant. Für die exakte Bestimmung von ${\it \Phi}_x(f)$ sind zwei Grenzübergänge notwendig:
- $${{\it \Phi}_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$
$\text{Fazit:}$
- Aus dieser physikalischen Interpretation folgt weiter, dass das Leistungsdichtespektrum stets reell ist und nie negativ werden kann.
- Die gesamte Signalleistung von $x(t)$ erhält man dann durch Integration über alle Spektralanteile:
- $$P_x = \int^{\infty}_{0}{\it \Phi}_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}{\it \Phi}_x(f)\hspace{0.1cm} {\rm d} f .$$
Reziprozitätsgesetz von AKF-Zeitdauer und LDS-Bandbreite
Alle im Buch „Signaldarstellung” für deterministische Signale hergeleiteten Gesetzmäßigkeiten der Fouriertransformation können auch auf die
- Autokorrelationsfunktion $\rm (AKF)$ und
- das Leistungsdichtespektrum $\rm (LDS)$
eines Zufallsprozesses angewendet werden. Aufgrund der spezifischen Eigenschaften
- von Autokorrelationsfunktion (stets reell und gerade)
- und Leistungsdichtespektrum (stets reell, gerade und nicht–negativ)
liefern allerdings nicht alle Gesetze sinnvolle Ergebnisse.
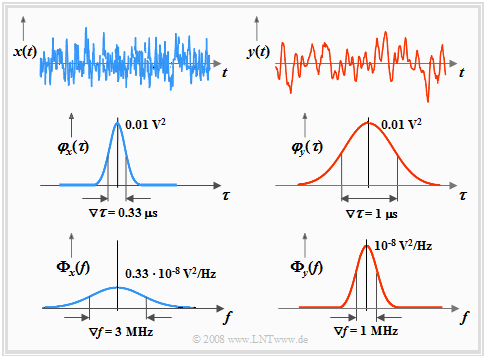
Wir betrachten nun wie im Abschnitt "Interpretation der Autokorrelationsfunktion" zwei unterschiedliche ergodische Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ anhand
- der beiden Mustersignale $x(t)$ und $y(t)$ ⇒ obere Skizze,
- der beiden Autokorrelationsfunktionen $φ_x(τ)$ und $φ_y(τ)$ ⇒ mittlere Skizze,
- der beiden Leistungsdichtespektren ${\it \Phi}_x(f)$ und ${\it \Phi}_y(f)$ ⇒ untere Skizze.
Anhand dieser beispielhaften Grafiken sind folgende Aussagen möglich:
- Die Flächen unter den LDS-Kurven sind gleich ⇒ die Prozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ besitzen hier gleiche Leistung:
- $${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$
- Das aus der klassischen (deterministischen) Systemtheorie bekannte "Reziprozitätsgesetz von Zeitdauer und Bandbreite" gilt hier ebenfalls: Eine schmale Autokorrelationsfunktion entspricht einem breiten Leistungsdichtespektrum und umgekehrt.
- Als Beschreibungsgröße verwenden wir hier die äquivalente LDS-Bandbreite $∇f$ $($man spricht„Nabla-f”$)$, ähnlich definiert wie die äquivalente AKF-Dauer $∇τ$ im Kapitel "Interpretation der Autokorrelationsfunktion":
- $${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, \hspace{0.5cm}{ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$
- Mit diesen Definitionen gilt der folgende grundlegende Zusammenhang:
- $${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm bzw.}\hspace{1cm} {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$
$\text{Beispiel 1:}$ Wir gehen von der oberen Grafik auf dieser Seite aus:
- Die Kenngrößen des höherfrequenten Signals $x(t)$ sind $∇τ_x = 0.33\hspace{0.08cm} \rm µs$ und $∇f_x = 3 \hspace{0.08cm} \rm MHz$.
- Die äquivalente AKF-Dauer des Signals $y(t)$ ist dreimal so groß: $∇τ_y = 1 \hspace{0.08cm} \rm µs$.
- Dessen äquivalente LDS-Bandbreite beträgt somit nur mehr $∇f_y = ∇f_x/3 = 1 \hspace{0.08cm} \rm MHz$.
$\text{Allgemein gilt:}$ Das Produkt aus äquivalenter AKF-Dauer ${ {\rm \nabla} \tau_x}$ und äquivalenter LDS-Bandbreite $ { {\rm \nabla} f_x}$ ist immer gleich $1$:
- $${ {\rm \nabla} \tau_x} \cdot { {\rm \nabla} f_x} = 1.$$
$\text{Beweis:}$ Entsprechend den obigen Definitionen gilt:
- $${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac { {\it \Phi}_x(f = {\rm 0)} }{ \varphi_x(\tau = \rm 0)},$$
- $${ {\rm \nabla} f_x} = \frac {1}{ {\it \Phi}_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{ {\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)} }{ {\it \Phi}_x(f = \rm 0)}.$$
Das Produkt ist somit gleich $1$.
$\text{Beispiel 2:}$ Ein Grenzfall des Reziprozitätsgesetzes stellt das so genannte Weiße Rauschen dar:
- Dieses beinhaltet alle Spektralanteile (bis ins Unendliche).
- Die äquivalente LDS-Bandbreite $∇f$ ist also unendlich groß.
Das hier angegebene Gesetz besagt, dass damit für die äquivalente AKF-Dauer $∇τ = 0$ gelten muss ⇒ Weißes Rauschen besitzt stets eine diracförmige AKF.
Mehr zu dieser Thematik finden Sie im dreiteiligen Lernvideo "Der AWGN-Kanal", insbesondere im zweiten Teil.
Leistungsdichtespektrum mit Gleichsignalkomponente
Wir gehen von einem gleichsignalfreien Zufallsprozess $\{x_i(t)\}$ aus. Weiter setzen wir voraus, dass der Prozess auch keine periodischen Anteile beinhaltet. Dann gilt:
- Die Autokorrelationsfunktion $φ_x(τ)$ verschwindet für $τ → ∞$.
- Das Leistungsdichtespektrum ${\it \Phi}_x(f)$ – berechenbar als die Fouriertransformierte von $φ_x(τ)$ – ist sowohl wert– als auch zeitkontinuierlich, also ohne diskrete Anteile.
Wir betrachten nun einen zweiten Zufallsprozess $\{y_i(t)\}$, der sich vom Prozess $\{x_i(t)\}$ lediglich durch eine zusätzliche Gleichsignalkomponente $m_y$ unterscheidet:
- $$\left\{ y_i (t) \right\} = \left\{ x_i (t) + m_y \right\}.$$
Die statistischen Beschreibungsgrößen des mittelwertbehafteten Zufallsprozesses $\{y_i(t)\}$ weisen dann folgende Eigenschaften auf:
- Der Grenzwert der AKF für $τ → ∞$ ist nun nicht mehr Null, sondern $m_y^2$. Im gesamten $τ$–Bereich von $–∞$ bis $+∞$ ist die AKF $φ_y(τ)$ um $m_y^2$ größer als $φ_x(τ)$:
- $${\varphi_y ( \tau)} = {\varphi_x ( \tau)} + m_y^2 . $$
- Nach den elementaren Gesetzen der Fouriertransformation führt der konstante AKF-Beitrag im LDS zu einer Diracfunktion $δ(f)$ mit dem Gewicht $m_y^2$:
- $${{\it \Phi}_y ( f)} = {\Phi_x ( f)} + m_y^2 \cdot \delta (f). $$
- Nähere Informationen zur Diracfunktion finden Sie im Kapitel "Gleichsignal - Grenzfall eines periodischen Signals" des Buches „Signaldarstellung”. Zudem möchten wir Sie hier auf das Lernvideo "Herleitung und Visualisierung der Diracfunktion" hinweisen.
Numerische LDS-Ermittlung
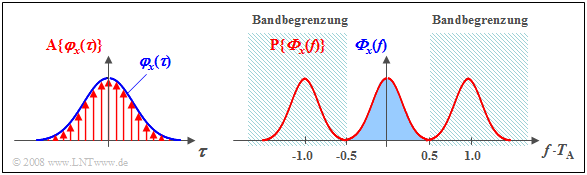
Autokorrelationsfunktion und Leistungsdichtespektrum sind über die Fouriertransformation streng miteinander verknüpft. Dieser Zusammenhang gilt auch bei zeitdiskreter AKF-Darstellung mit dem Abtastoperator ${\rm A} \{ \varphi_x ( \tau ) \} $, also für
- $${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$
Der Übergang vom Zeit– in den Spektralbereich kann mit folgenden Schritten hergeleitet werden:
- Der Abstand $T_{\rm A}$ zweier Abtastwerte ist durch die absolute Bandbreite $B_x$ $($maximal auftretende Frequenz innerhalb des Prozesses$)$ über das Abtasttheorem festgelegt:
- $$T_{\rm A}\le\frac{1}{2B_x}.$$
- Die Fouriertransformierte der zeitdiskreten $($abgetasteten$)$ Autokorrelationsfunktion ergibt ein mit ${\rm 1}/T_{\rm A}$ periodisches Leistungsdichtespektrum:
- $${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{{\it \Phi}_x} ( f) \} = \sum_{\mu = - \infty}^{\infty} {{\it \Phi}_x} ( f - \frac {\mu}{T_{\rm A}}).$$
$\text{Fazit:}$ Da sowohl $φ_x(τ)$ als auch ${\it \Phi}_x(f)$ gerade und reelle Funktionen sind, gilt der Zusammenhang:
- $${\rm P} \{ { {\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{\infty} \varphi_x ( k T_{\rm A}) \cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$
- Das Leistungsdichtespektrum (LDS) des zeitkontinuierlichen Prozesses erhält man aus ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ durch Bandbegrenzung auf den Bereich $\vert f \vert ≤ 1/(2T_{\rm A})$.
- Im Zeitbereich bedeutet diese Operation eine Interpolation der einzelnen AKF-Abtastwerte mit der ${\rm si}$–Funktion, wobei ${\rm si}(x)$ für $\sin(x)/x$ steht.
$\text{Beispiel 3:}$ Eine gaußförmige AKF $φ_x(τ)$ wird im Abstand $T_{\rm A}$ abgetastet, wobei das Abtasttheorem erfüllt ist:
- Die Fouriertransformierte der zeitdiskreten Autokorrelationsfunktion ${\rm A} \{φ_x(τ) \}$ sei ${\rm P} \{ { {\it \Phi}_x} ( f) \}$.
- Diese mit ${\rm 1}/T_{\rm A}$ periodische Funktion ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ ist dementsprechend unendlich weit ausgedehnt (roter Kurvenzug).
- Das Leistungsdichtespektrum ${\it \Phi}_x(f)$ des zeitkontinuierlichen Prozesses $\{x_i(t)\}$ erhält man durch Bandbegrenzung auf den im Bild blau hinterlegten Frequenzbereich $\vert f · T_{\rm A} \vert ≤ 0.5$.
Genauigkeit der numerischen LDS-Berechnung
Für die nachfolgende Analyse gehen wir von folgenden Annahmen aus:
- Die zeitdiskrete AKF $φ_x(k · T_{\rm A})$ wurde aus $N$ Abtastwerten numerisch ermittelt.
- Wie auf der Seite "Genauigkeit der numerischen AKF-Berechnung" gezeigt, sind diese Werte fehlerhaft und die Fehler korreliert, wenn $N$ zu klein gewählt wurde.
- Zur Berechnung des periodischen Leistungsdichtespektrums $\rm (LDS)$ verwenden wir nur die AKF-Werte $φ_x(0)$, ... , $φ_x(K · T_{\rm A})$:
- $${\rm P} \{{{\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{K} \varphi_x ( k T_{\rm A})\cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$
$\text{Fazit:}$ Die Genauigkeit der LDS-Berechnung wird im starken Maße durch den Parameter $K$ bestimmt:
- Ist $K$ zu klein gewählt, so werden die eigentlich vorhandenen AKF-Werte $φ_x(k · T_{\rm A})$ mit $k > K$ nicht berücksichtigt.
- Bei zu großem $K$ werden auch solche AKF-Werte berücksichtigt, die eigentlich Null sein sollten und nur wegen der numerischen AKF-Berechnung endlich sind.
- Diese Werte sind allerdings – bedingt durch ein zu kleines $N$ bei der AKF–Ermittlung – nur Fehler, und beinträchtigen die LDS-Berechnung mehr als dass sie einen brauchbaren Beitrag zum Ergebnis liefern.
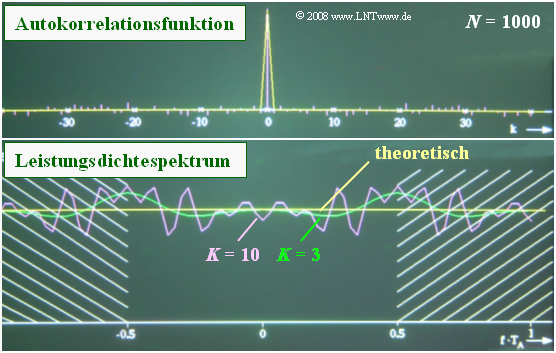
$\text{Beispiel 4:}$ Wir betrachten hier einen mittelwertfreien Prozess mit statistisch unabhängigen Abtastwerten. Deshalb sollte eigentlich nur der AKF–Wert $φ_x(0) = σ_x^2$ von Null verschieden sein.
- Ermittelt man aber die AKF numerisch aus lediglich $N = 1000$ Abtastwerten, so erhält man auch für $k ≠ 0$ endliche AKF–Werte.
- Das obere Bild zeigt, dass diese fehlerhaften AKF–Werte bis zu $6\%$ des Maximalwertes betragen können.
- Unten ist das numerisch ermittelte LDS dargestellt. Der theoretische Verlauf (gelbe Kurve) sollte für $\vert f · T_{\rm A} \vert ≤ 0.5$ konstant sein.
- Die grüne und die violette Kurve verdeutlichen, wie durch $K = 3$ bzw. $K = 10$ das Ergebnis gegenüber $K = 0$ verfälscht wird.
Im betrachteten Fall (statistisch unabhängige Zufallsgrößen) wächst der Fehler monoton mit steigendem $K$. Bei einer Zufallsgröße mit statistischen Bindungen gibt es dagegen jeweils einen optimalen Wert für $K$.
- Wird dieser zu klein gewählt, so werden signifikante Bindungen nicht berücksichtigt.
- Ein zu großer Wert führt dagegen zu Oszillationen, die vorwiegend auf fehlerhafte AKF–Werte zurückzuführen sind.
Aufgaben zum Kapitel
Aufgabe 4.12: Leistungsdichtespektrum eines Binärsignals
Aufgabe 4.12Z: Weißes Rauschen