Aufgaben:Aufgabe 4.11: Frequenzbereichsbetrachtung der 4–QAM: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
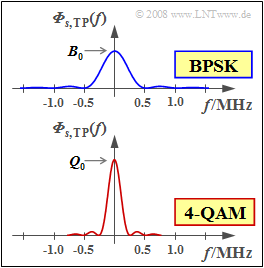
| − | [[Datei: | + | [[Datei:Mod_A_4_10_vers2.png|right|frame|Leistungsdichtespektren von <br>BPSK und 4-QAM]] |
| − | Ausgehend von der [[Modulationsverfahren/Lineare_digitale_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|BPSK]] (binäre Phasenmodulation) mit rechteckförmigem Grundimpuls $g_s(t)$ der Breite $T_{\rm B} = 1 \ \rm | + | Ausgehend von der [[Modulationsverfahren/Lineare_digitale_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|BPSK]] (binäre Phasenmodulation) mit rechteckförmigem Grundimpuls $g_s(t)$ der Breite $T_{\rm B} = 1 \ \rm µ s$ und der Amplitude $s_0 = 2 \ \rm V$ soll das Leistungsdichtespektrum $\rm (LDS)$ der [[Modulationsverfahren/Quadratur–Amplitudenmodulation#Signalverl.C3.A4ufe_der_4.E2.80.93QAM|4–QAM]] schrittweise ermittelt werden. |
| − | In der [[Aufgaben:4.7_Spektren_von_ASK_und_BPSK| Aufgabe 4.7]] wurde das Leistungdichtespektrum ${\it Φ}_s(f)$ der BPSK für genau diese Parameterwerte ermittelt. Mit | + | In der [[Aufgaben:4.7_Spektren_von_ASK_und_BPSK| Aufgabe 4.7]] wurde das Leistungdichtespektrum ${\it Φ}_s(f)$ der BPSK für genau diese Parameterwerte ermittelt. Mit |
:$$A = s_0^2 \cdot T_{\rm B} = 4 \cdot 10^{-6}\,{\rm V^2/Hz}$$ | :$$A = s_0^2 \cdot T_{\rm B} = 4 \cdot 10^{-6}\,{\rm V^2/Hz}$$ | ||
| − | erhält man für das tatsächliche Leistungsdichtespektrum (im Bandpassbereich): | + | erhält man für das tatsächliche Leistungsdichtespektrum (im Bandpassbereich): |
| − | :$${{\it \Phi}_s(f)} = {A}/{4} \cdot {\ | + | :$${{\it \Phi}_s(f)} = {A}/{4} \cdot {\big [ {\rm si}^2(\pi \cdot T_{\rm B}\cdot (f - f_{\rm T})) + {\rm si}^2(\pi \cdot T_{\rm B}\cdot (f + f_{\rm T}))\big ]}\hspace{0.05cm}.$$ |
| − | In der oberen Grafik ist allerdings das Leistungsdichtespektrum ${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}$ des äquivalenten Tiefpass–Signals dargestellt. Dieses ergibt sich aus ${\it Φ}_s(f)$ durch | + | In der oberen Grafik ist allerdings das Leistungsdichtespektrum ${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}$ des äquivalenten Tiefpass–Signals dargestellt. Dieses ergibt sich aus ${\it Φ}_s(f)$ durch |
*Abschneiden aller Anteile bei negativen Frequenzen, | *Abschneiden aller Anteile bei negativen Frequenzen, | ||
| − | *Vervierfachen der Anteile bei positiven Frequenzen ( | + | *Vervierfachen der Anteile bei positiven Frequenzen (weil: ein Spektrum muss verdoppelt werden, ein LDS vervierfacht), |
| − | *Verschieben um $f_{\rm T}$ nach links: | + | *Verschieben um $f_{\rm T}$ nach links: |
:$${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)} = A \cdot {\rm si}^2(\pi f T_{\rm B}). \hspace{0.2cm}$$ | :$${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)} = A \cdot {\rm si}^2(\pi f T_{\rm B}). \hspace{0.2cm}$$ | ||
Die 4–QAM unterscheidet sich von der BPSK in folgenden Details: | Die 4–QAM unterscheidet sich von der BPSK in folgenden Details: | ||
| − | * Aufspaltung des binären Quellensignals in zwei Teilsignale mit jeweils halber Bitrate, das heißt mit der Symboldauer $T = 2 · T_{\rm B}$. | + | * Aufspaltung des binären Quellensignals in zwei Teilsignale mit jeweils halber Bitrate, das heißt mit der Symboldauer $T = 2 · T_{\rm B}$. |
| − | * Multiplikation der Teilsignale mit Cosinus und Minus–Sinus, deren Amplituden $g_0$ jeweils um den Faktor $\sqrt{2}$ kleiner sind als $s_0$. | + | * Multiplikation der Teilsignale mit Cosinus und Minus–Sinus, deren Amplituden $g_0$ jeweils um den Faktor $\sqrt{2}$ kleiner sind als $s_0$. |
| − | * Summation der beiden Teilsignale, die mit $s_{\cos}(t)$ und $s_{–\sin}(t)$ bezeichnet werden: | + | * Summation der beiden Teilsignale, die mit $s_{\cos}(t)$ und $s_{–\sin}(t)$ bezeichnet werden: |
:$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$ | :$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation|Quadratur–Amplitudenmodulation]]. | + | |
| − | *Bezug genommen wird aber auch auf die Seite [[Modulationsverfahren/Lineare_digitale_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|BPSK – Binary Phase Shift Keying]] im vorherigen Kapitel. | + | |
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation|"Quadratur–Amplitudenmodulation"]]. | ||
| + | *Bezug genommen wird aber auch auf die Seite [[Modulationsverfahren/Lineare_digitale_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|"BPSK – Binary Phase Shift Keying"]] im vorherigen Kapitel. | ||
* Das Leistungsdichtespektrum (LDS) einer QAM-Komponente ist identisch mit dem vergleichbaren BPSK–LDS. | * Das Leistungsdichtespektrum (LDS) einer QAM-Komponente ist identisch mit dem vergleichbaren BPSK–LDS. | ||
| − | *Energien sind in $\rm V^2s$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$. | + | *Energien sind in $\rm V^2s$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$. |
| − | + | ||
| Zeile 34: | Zeile 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die Energie pro Bit ⇒ $E_{\rm B}$ bei | + | {Wie groß ist die Energie pro Bit ⇒ $E_{\rm B}$ bei "Binary Phase Shift Keying" (BPSK)? |
|type="{}"} | |type="{}"} | ||
$E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | $E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | ||
| − | {Wie lautet das Leistungsdichtespektrum ${\it \Phi}_{s,\hspace{0.08cm} \cos, \hspace{0.08cm}{\rm TP}}(f )$ des 4–QAM–Teilsignals $s_{\cos}(t)$ in der äquivalenten Tiefpassdarstellung? <br>Welcher Wert $B_0 = {\it \Phi}_{s, \hspace{0.08cm}\cos, \hspace{0.08cm}{\rm TP}}(f = 0) $ ergibt sich bei der Frequenz $f = 0$? | + | {Wie lautet das Leistungsdichtespektrum ${\it \Phi}_{s,\hspace{0.08cm} \cos, \hspace{0.08cm}{\rm TP}}(f )$ des 4–QAM–Teilsignals $s_{\cos}(t)$ in der äquivalenten Tiefpassdarstellung? <br>Welcher Wert $B_0 = {\it \Phi}_{s, \hspace{0.08cm}\cos, \hspace{0.08cm}{\rm TP}}(f = 0) $ ergibt sich bei der Frequenz $f = 0$? |
|type="{}"} | |type="{}"} | ||
$B_0 \ = \ $ { 4 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | $B_0 \ = \ $ { 4 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | ||
| − | {Wie lautet das Leistungsdichtespektrum ${\it \Phi}_{s,\hspace{0.08cm}{\rm TP}}(f )$ des gesamten 4–QAM–Signals $s(t)$? | + | {Wie lautet das Leistungsdichtespektrum ${\it \Phi}_{s,\hspace{0.08cm}{\rm TP}}(f )$ des gesamten 4–QAM–Signals $s(t)$? |
| − | Welcher Wert $Q_0 = {\it \Phi}_{s, \hspace{0.08cm}{\rm TP}}(f = 0) $ ergibt sich hier bei der Frequenz $f = 0$? | + | <br>Welcher Wert $Q_0 = {\it \Phi}_{s, \hspace{0.08cm}{\rm TP}}(f = 0) $ ergibt sich hier bei der Frequenz $f = 0$? |
|type="{}"} | |type="{}"} | ||
$Q_0 \ = \ $ { 8 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | $Q_0 \ = \ $ { 8 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | ||
| − | {Wie groß ist die Energie pro Bit ⇒ $E_{\rm B}$ bei der | + | {Wie groß ist die Energie pro Bit ⇒ $E_{\rm B}$ bei der "Quadratur–Amplitudenmodulation" (4–QAM)? |
|type="{}"} | |type="{}"} | ||
$E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | $E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | ||
| Zeile 57: | Zeile 60: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die Leistung des BPSK–Sendesignals ist gleich dem Intergral über das Leistungsdichtespektrum. Integriert man über das äquivalente Tiefpass–LDS, so ist noch der Faktor 1/2 zu berücksichtigen: | + | '''(1)''' Die Leistung des BPSK–Sendesignals ist gleich dem Intergral über das Leistungsdichtespektrum. |
| + | *Integriert man über das äquivalente Tiefpass–LDS, so ist noch der Faktor $1/2$ zu berücksichtigen: | ||
:$$P_{\rm BPSK} = \int_{ - \infty }^{+\infty} {{\it \Phi}_{s}(f)}\hspace{0.1cm} {\rm d}f = \frac{1}{2} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{A}{2} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{A}{2T_{\rm B}} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi x)\hspace{0.1cm} {\rm d}x =\frac{A}{2T_{\rm B}}$$ | :$$P_{\rm BPSK} = \int_{ - \infty }^{+\infty} {{\it \Phi}_{s}(f)}\hspace{0.1cm} {\rm d}f = \frac{1}{2} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{A}{2} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{A}{2T_{\rm B}} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi x)\hspace{0.1cm} {\rm d}x =\frac{A}{2T_{\rm B}}$$ | ||
:$$\text{Mit} \ \ A = 4 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}, \hspace{0.2cm} T_{\rm B}= 10^{-6}\,{\rm s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm BPSK} = 2\,{\rm V^2} ( = {s_0^2 }/{2})\hspace{0.05cm}.$$ | :$$\text{Mit} \ \ A = 4 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}, \hspace{0.2cm} T_{\rm B}= 10^{-6}\,{\rm s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm BPSK} = 2\,{\rm V^2} ( = {s_0^2 }/{2})\hspace{0.05cm}.$$ | ||
| − | Die Energie pro Bit ist dementsprechend bei der BPSK: | + | *Die Energie pro Bit ist dementsprechend bei der BPSK: |
:$$E_{\rm B} = {P_{\rm BPSK} \cdot T_{\rm B}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | :$$E_{\rm B} = {P_{\rm BPSK} \cdot T_{\rm B}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | ||
| − | Hierbei ist wieder der Bezugswiderstand $1\ \rm Ω$ zugrunde gelegt. | + | *Hierbei ist wieder der Bezugswiderstand $1\ \rm Ω$ zugrunde gelegt. |
| − | '''(2)''' Aufgrund der doppelten Symboldauer der 4–QAM ( | + | |
| + | |||
| + | '''(2)''' Aufgrund der doppelten Symboldauer der 4–QAM $(T = 2 · T_{\rm B})$ ist die Spektralfunktion gegenüber der BPSK nur halb so breit, aber doppelt so hoch, und anstelle von $s_0$ ist nun der kleinere Wert $g_0$ zu berücksichtigen. | ||
| + | *Der LDS–Wert bei der Frequenz $f = 0$ lautet damit: | ||
:$${\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) = \left ({s_0}/{\sqrt{2}} \right )^2 \cdot 2 \cdot T_{\rm B} ={s_0^2 \cdot T_{\rm B}} = B_0 \hspace{0.05cm}.$$ | :$${\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) = \left ({s_0}/{\sqrt{2}} \right )^2 \cdot 2 \cdot T_{\rm B} ={s_0^2 \cdot T_{\rm B}} = B_0 \hspace{0.05cm}.$$ | ||
| − | Es ergibt sich somit genau der gleiche Wert wie bei der BPSK: | + | *Es ergibt sich somit genau der gleiche Wert wie bei der BPSK: |
:$$B_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) \hspace{0.15cm}\underline {= 4 \cdot 10^{-6}\,{\rm V^2/Hz}}$$ | :$$B_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) \hspace{0.15cm}\underline {= 4 \cdot 10^{-6}\,{\rm V^2/Hz}}$$ | ||
| − | '''(3)''' Das zweite Teilsignal $s_{–\sin}(t)$ liefert den genau gleichen Beitrag wie das gerade betrachtete Signal $s_{\cos}(t)$. Aufgrund der Orthogonalität zwischen der Cosinus– und der Minus–Sinusfunktion können die Leistungen addiert werden und man erhält: | + | |
| − | $$Q_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f = 0 ) = 2 \cdot B_0 \hspace{0.15cm}\underline {= 8 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | + | '''(3)''' Das zweite Teilsignal $s_{–\sin}(t)$ liefert den genau gleichen Beitrag wie das gerade betrachtete Signal $s_{\cos}(t)$. |
| + | *Aufgrund der Orthogonalität zwischen der Cosinus– und der Minus–Sinusfunktion können die Leistungen addiert werden und man erhält: | ||
| + | :$$Q_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f = 0 ) = 2 \cdot B_0 \hspace{0.15cm}\underline {= 8 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | ||
| + | |||
| − | '''(4)''' Analog zur Teilaufgabe (1) erhält man für die Energie pro Bit: | + | '''(4)''' Analog zur Teilaufgabe '''(1)''' erhält man für die Energie pro Bit: |
:$$E_{\rm B} = \frac{1}{2} \cdot T_{\rm B} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi f T_{\rm B})\hspace{0.1cm} {\rm d}f = | :$$E_{\rm B} = \frac{1}{2} \cdot T_{\rm B} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi f T_{\rm B})\hspace{0.1cm} {\rm d}f = | ||
\frac{Q_0 \cdot T_{\rm B}}{2T} = \frac{8 \cdot 10^{-6}\,{\rm V^2/Hz} \cdot 1\,{\rm \mu s}}{ 2 \cdot 2\,{\rm \mu s}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | \frac{Q_0 \cdot T_{\rm B}}{2T} = \frac{8 \cdot 10^{-6}\,{\rm V^2/Hz} \cdot 1\,{\rm \mu s}}{ 2 \cdot 2\,{\rm \mu s}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | ||
| − | Man erkennt, dass bei den hier getroffenen Voraussetzungen die „Energie pro Bit” von BPSK und 4–QAM übereinstimmen. | + | *Man erkennt, dass bei den hier getroffenen Voraussetzungen die „Energie pro Bit” von BPSK und 4–QAM übereinstimmen. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 18. April 2022, 06:14 Uhr
Ausgehend von der BPSK (binäre Phasenmodulation) mit rechteckförmigem Grundimpuls $g_s(t)$ der Breite $T_{\rm B} = 1 \ \rm µ s$ und der Amplitude $s_0 = 2 \ \rm V$ soll das Leistungsdichtespektrum $\rm (LDS)$ der 4–QAM schrittweise ermittelt werden.
In der Aufgabe 4.7 wurde das Leistungdichtespektrum ${\it Φ}_s(f)$ der BPSK für genau diese Parameterwerte ermittelt. Mit
- $$A = s_0^2 \cdot T_{\rm B} = 4 \cdot 10^{-6}\,{\rm V^2/Hz}$$
erhält man für das tatsächliche Leistungsdichtespektrum (im Bandpassbereich):
- $${{\it \Phi}_s(f)} = {A}/{4} \cdot {\big [ {\rm si}^2(\pi \cdot T_{\rm B}\cdot (f - f_{\rm T})) + {\rm si}^2(\pi \cdot T_{\rm B}\cdot (f + f_{\rm T}))\big ]}\hspace{0.05cm}.$$
In der oberen Grafik ist allerdings das Leistungsdichtespektrum ${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}$ des äquivalenten Tiefpass–Signals dargestellt. Dieses ergibt sich aus ${\it Φ}_s(f)$ durch
- Abschneiden aller Anteile bei negativen Frequenzen,
- Vervierfachen der Anteile bei positiven Frequenzen (weil: ein Spektrum muss verdoppelt werden, ein LDS vervierfacht),
- Verschieben um $f_{\rm T}$ nach links:
- $${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)} = A \cdot {\rm si}^2(\pi f T_{\rm B}). \hspace{0.2cm}$$
Die 4–QAM unterscheidet sich von der BPSK in folgenden Details:
- Aufspaltung des binären Quellensignals in zwei Teilsignale mit jeweils halber Bitrate, das heißt mit der Symboldauer $T = 2 · T_{\rm B}$.
- Multiplikation der Teilsignale mit Cosinus und Minus–Sinus, deren Amplituden $g_0$ jeweils um den Faktor $\sqrt{2}$ kleiner sind als $s_0$.
- Summation der beiden Teilsignale, die mit $s_{\cos}(t)$ und $s_{–\sin}(t)$ bezeichnet werden:
- $$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Quadratur–Amplitudenmodulation".
- Bezug genommen wird aber auch auf die Seite "BPSK – Binary Phase Shift Keying" im vorherigen Kapitel.
- Das Leistungsdichtespektrum (LDS) einer QAM-Komponente ist identisch mit dem vergleichbaren BPSK–LDS.
- Energien sind in $\rm V^2s$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$.
Fragebogen
Musterlösung
- Integriert man über das äquivalente Tiefpass–LDS, so ist noch der Faktor $1/2$ zu berücksichtigen:
- $$P_{\rm BPSK} = \int_{ - \infty }^{+\infty} {{\it \Phi}_{s}(f)}\hspace{0.1cm} {\rm d}f = \frac{1}{2} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{A}{2} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{A}{2T_{\rm B}} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi x)\hspace{0.1cm} {\rm d}x =\frac{A}{2T_{\rm B}}$$
- $$\text{Mit} \ \ A = 4 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}, \hspace{0.2cm} T_{\rm B}= 10^{-6}\,{\rm s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm BPSK} = 2\,{\rm V^2} ( = {s_0^2 }/{2})\hspace{0.05cm}.$$
- Die Energie pro Bit ist dementsprechend bei der BPSK:
- $$E_{\rm B} = {P_{\rm BPSK} \cdot T_{\rm B}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$
- Hierbei ist wieder der Bezugswiderstand $1\ \rm Ω$ zugrunde gelegt.
(2) Aufgrund der doppelten Symboldauer der 4–QAM $(T = 2 · T_{\rm B})$ ist die Spektralfunktion gegenüber der BPSK nur halb so breit, aber doppelt so hoch, und anstelle von $s_0$ ist nun der kleinere Wert $g_0$ zu berücksichtigen.
- Der LDS–Wert bei der Frequenz $f = 0$ lautet damit:
- $${\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) = \left ({s_0}/{\sqrt{2}} \right )^2 \cdot 2 \cdot T_{\rm B} ={s_0^2 \cdot T_{\rm B}} = B_0 \hspace{0.05cm}.$$
- Es ergibt sich somit genau der gleiche Wert wie bei der BPSK:
- $$B_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) \hspace{0.15cm}\underline {= 4 \cdot 10^{-6}\,{\rm V^2/Hz}}$$
(3) Das zweite Teilsignal $s_{–\sin}(t)$ liefert den genau gleichen Beitrag wie das gerade betrachtete Signal $s_{\cos}(t)$.
- Aufgrund der Orthogonalität zwischen der Cosinus– und der Minus–Sinusfunktion können die Leistungen addiert werden und man erhält:
- $$Q_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f = 0 ) = 2 \cdot B_0 \hspace{0.15cm}\underline {= 8 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$
(4) Analog zur Teilaufgabe (1) erhält man für die Energie pro Bit:
- $$E_{\rm B} = \frac{1}{2} \cdot T_{\rm B} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} = \frac{8 \cdot 10^{-6}\,{\rm V^2/Hz} \cdot 1\,{\rm \mu s}}{ 2 \cdot 2\,{\rm \mu s}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$
- Man erkennt, dass bei den hier getroffenen Voraussetzungen die „Energie pro Bit” von BPSK und 4–QAM übereinstimmen.