Aufgaben:Aufgabe 2.2: Binäre bipolare Rechtecke: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Grundlagen der codierten Übertragung | {{quiz-Header|Buchseite=Digitalsignalübertragung/Grundlagen der codierten Übertragung | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
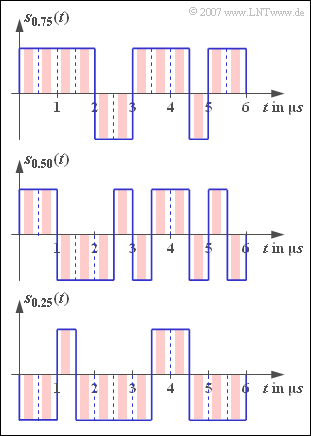
[[Datei:P_ID1310__Dig_A_2_2.png|right|frame|Beispiele für binäre bipolare Rechtecksignale]] | [[Datei:P_ID1310__Dig_A_2_2.png|right|frame|Beispiele für binäre bipolare Rechtecksignale]] | ||
Wir gehen von folgendem Signal aus: | Wir gehen von folgendem Signal aus: | ||
:$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$ | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$ | ||
| − | Der Sendegrundimpuls $g_{s}(t)$ wird in dieser Aufgabe stets als rechteckförmig angenommen, wobei das NRZ–Format (blaue Signalverläufe in der Grafik) als auch das RZ–Format mit dem Tastverhältnis $T_{\rm S}/T = 0.5$ (rote Signalverläufe) zu untersuchen ist. | + | Der Sendegrundimpuls $g_{s}(t)$ wird in dieser Aufgabe stets als rechteckförmig angenommen, wobei das NRZ–Format (blaue Signalverläufe in der Grafik) als auch das RZ–Format mit dem Tastverhältnis $T_{\rm S}/T = 0.5$ (rote Signalverläufe) zu untersuchen ist. |
Die Amplitudenkoeffizienten besitzen die folgenden Eigenschaften: | Die Amplitudenkoeffizienten besitzen die folgenden Eigenschaften: | ||
| − | *Sie sind binär und bipolar: $a_{\nu} | + | *Sie sind binär und bipolar: $a_{\nu} \in \{–1, +1\}$. |
| − | *$\langle a_{\nu }\rangle$ | + | *Die Symbole innerhalb der Folge $\langle a_{\nu }\rangle$ weisen keine statistischen Bindungen auf. |
| − | *Die Wahrscheinlichkeiten für die beiden möglichen Werte $±1$ lauten mit $0 < p < 1$: | + | *Die Wahrscheinlichkeiten für die beiden möglichen Werte $±1$ lauten mit $0 < p < 1$: |
:$${\rm Pr}(a_\nu = +1) \ = \ p,$$ | :$${\rm Pr}(a_\nu = +1) \ = \ p,$$ | ||
:$${\rm Pr}(a_\nu = -1) \ = \ 1 - p \hspace{0.05cm}.$$ | :$${\rm Pr}(a_\nu = -1) \ = \ 1 - p \hspace{0.05cm}.$$ | ||
| − | Die drei in der Grafik dargestellten Signalausschnitte gelten für $p = 0.75$, $p = 0.50$ und $p = 0.25$. | + | Die drei in der Grafik dargestellten Signalausschnitte gelten für $p = 0.75$, $p = 0.50$ und $p = 0.25$. |
| + | |||
Im Laufe dieser Aufgabe wird auf folgende Beschreibungsgrößen Bezug genommen: | Im Laufe dieser Aufgabe wird auf folgende Beschreibungsgrößen Bezug genommen: | ||
| − | *$m_{a} = \E[a_{\nu}]$ gibt den linearen Mittelwert der Amplitudenkoeffizienten an | + | *$m_{a} = \E\big[a_{\nu}\big]$ gibt den linearen Mittelwert der Amplitudenkoeffizienten an. |
| − | *Die diskrete AKF der Amplitudenkoeffizienten ist $\varphi_{a}(\lambda) = \E[a_{\nu} \cdot a_{\nu} + \lambda]$. Es gilt hier: | + | |
| + | *$m_{2a} = \E\big[a_{\nu}^{2}\big]$ ist das Moment zweiter Ordnung ("Leistung"). | ||
| + | |||
| + | *Damit kann auch die Varianz $\sigma_{a}^{2} = m_{2a} - m_{a}^{2}$ berechnet werden. | ||
| + | |||
| + | *Die diskrete AKF der Amplitudenkoeffizienten ist $\varphi_{a}(\lambda) = \E\big[a_{\nu} \cdot a_{\nu} + \lambda \big]$. Es gilt hier: | ||
:$$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 \\ m_1^2 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \hspace{0.05cm}.\\ \end{array}$$ | :$$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 \\ m_1^2 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \hspace{0.05cm}.\\ \end{array}$$ | ||
*Die Energie–AKF des Sendegrundimpulses beträgt: | *Die Energie–AKF des Sendegrundimpulses beträgt: | ||
| − | :$$\varphi^{^{\bullet}}_{ | + | :$$\varphi^{^{\bullet}}_{g_s}(\tau) = \left\{ \begin{array}{c} s_0^2 \cdot T_{\rm S} \cdot \left( 1 - {|\tau|}/{T_{\rm S}}\right) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}|\tau| \le T_{\rm S} \\ |\tau| \ge T_{\rm S} \hspace{0.05cm}.\\ \end{array}$$ |
*Damit erhält man für die gesamte AKF des Sendesignals: | *Damit erhält man für die gesamte AKF des Sendesignals: | ||
| − | :$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{ | + | :$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{g_s}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$ |
| − | *Das Leistungsdichtespektrum $\ | + | *Das Leistungsdichtespektrum ${\it \Phi}_{s}(f)$ ist die Fouriertransformierte der AKF $\varphi_{s}(\tau)$. |
| − | |||
| − | + | Hinweis: Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Grundlagen_der_codierten_Übertragung|"Grundlagen der codierten Übertragung"]]. | |
| + | |||
| + | |||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Zeile 44: | Zeile 49: | ||
| − | {Wie groß ist | + | {Wie groß ist das zweite Moment $(m_{2a})$ der Amplitudenkoeffizienten in Abhängigkeit von $p$? |
|type="{}"} | |type="{}"} | ||
| − | $p = 0.75 : m_{2a} \ = \ $ { 1 3% } | + | $p = 0.75\text{:} \hspace{0.4cm} m_{2a} \ = \ $ { 1 3% } |
| − | $p = 0.50 : m_{2a} \ = \ $ { 1 3% } | + | $p = 0.50\text{:} \hspace{0.4cm} m_{2a} \ = \ $ { 1 3% } |
| − | $p = 0.25 : m_{2a} \ = \ $ { 1 3% } | + | $p = 0.25\text{:} \hspace{0.4cm} m_{2a} \ = \ $ { 1 3% } |
| − | {Berechnen Sie den linearen Mittelwert $m_{a}$ in Abhängigkeit von $p$. | + | {Berechnen Sie den linearen Mittelwert $m_{a}$ in Abhängigkeit von $p$. |
|type="{}"} | |type="{}"} | ||
| − | $p = 0.75 : m_{a} \ = \ $ { 0.5 3% } | + | $p = 0.75\text{:} \hspace{0.4cm} m_{a} \ = \ $ { 0.5 3% } |
| − | $p = 0.50 : m_{a} \ = \ $ { 0 3% } | + | $p = 0.50\text{:} \hspace{0.4cm} m_{a} \ = \ $ { 0 3% } |
| − | $p = 0.25 : m_{a} \ = \ $ { -0.515--0.485 } | + | $p = 0.25\text{:} \hspace{0.4cm} m_{a} \ = \ $ { -0.515--0.485 } |
| − | {Wie groß ist die Varianz $\sigma_{a}^{2}$ der Amplitudenkoeffizienten? | + | {Wie groß ist die Varianz $\sigma_{a}^{2}$ der Amplitudenkoeffizienten? |
|type="{}"} | |type="{}"} | ||
| − | $p = 0.75 : \sigma_{a}^{2} \ = \ $ { 0.75 3% } | + | $p = 0.75\text{:} \hspace{0.4cm} \sigma_{a}^{2} \ = \ $ { 0.75 3% } |
| − | $p = 0.50 : \sigma_{a}^{2} \ = \ $ { | + | $p = 0.50\text{:} \hspace{0.4cm} \sigma_{a}^{2} \ = \ $ { 1 3% } |
| − | $p = 0.25 : \sigma_{a}^{2} \ = \ $ { 0.75 3% } | + | $p = 0.25\text{:} \hspace{0.4cm} \sigma_{a}^{2} \ = \ $ { 0.75 3% } |
| − | {Es gelte zunächst $p = 0.5$. Skizzieren Sie die AKF $\varphi_{s}(\tau)$ für den NRZ– und den RZ–Grundimpuls und bewerten Sie folgende Aussagen: | + | {Es gelte zunächst $p = 0.5$. Skizzieren Sie die AKF $\varphi_{s}(\tau)$ für den NRZ– und den RZ–Grundimpuls und bewerten Sie folgende Aussagen: |
|type="[]"} | |type="[]"} | ||
+ Die AKF ist in beiden Fällen dreieckförmig. | + Die AKF ist in beiden Fällen dreieckförmig. | ||
| − | + Das LDS verläuft in beiden Fällen ${\rm si}^{2}$–förmig. | + | + Das LDS verläuft in beiden Fällen ${\rm si}^{2}$–förmig. |
-Die LDS–Fläche ist in beiden Fällen gleich. | -Die LDS–Fläche ist in beiden Fällen gleich. | ||
| − | -Bei RZ–Impulsen beinhaltet $\ | + | -Bei RZ–Impulsen beinhaltet ${\it \Phi}_{s}(f)$ zusätzliche Diracfunktionen. |
| − | {Es gelte nun $p = 0.75$. Skizzieren Sie die AKF für den NRZ–Grundimpuls und bewerten Sie folgende Aussagen: | + | {Es gelte nun $p = 0.75$. Skizzieren Sie die AKF für den NRZ–Grundimpuls und bewerten Sie folgende Aussagen: |
|type="[]"} | |type="[]"} | ||
+ Die AKF besteht aus einem Dreieck und einem Gleichanteil. | + Die AKF besteht aus einem Dreieck und einem Gleichanteil. | ||
| − | + Das LDS besteht aus einem ${\rm si}^{2}$–Anteil und einem Dirac. | + | + Das LDS besteht aus einem ${\rm si}^{2}$–Anteil und einem Dirac. |
| − | -Die Diracfunktion hat das Gewicht $s_{0}^{2}$. | + | -Die Diracfunktion hat das Gewicht $s_{0}^{2}$. |
| − | +Mit $p = 0.25$ ergibt sich das gleiche Leistungsdichtespektrum. | + | +Mit $p = 0.25$ ergibt sich das gleiche Leistungsdichtespektrum. |
| − | {Es gelte weiter $p = 0.75$. Skizzieren Sie die AKF für den RZ–Grundimpuls und bewerten Sie folgende | + | {Es gelte weiter $p = 0.75$. Skizzieren Sie die AKF für den RZ–Grundimpuls und bewerten Sie folgende Aussagen: |
|type="[]"} | |type="[]"} | ||
| − | + Auch hier beinhaltet das LDS einen ${\rm si}^{2}$–förmigen Anteil. | + | + Auch hier beinhaltet das LDS einen ${\rm si}^{2}$–förmigen Anteil. |
+ Gleichzeitig gibt es im LDS noch unendlich viele Diraclinien. | + Gleichzeitig gibt es im LDS noch unendlich viele Diraclinien. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
| Zeile 91: | Zeile 90: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Man spricht von einem redundanzfreien Digitalsignal, wenn | + | '''(1)''' Man spricht von einem redundanzfreien Digitalsignal, wenn |
| − | *die Amplitudenkoeffizienten nicht voneinander abhängen (dies wurde hier vorausgesetzt), | + | *die Amplitudenkoeffizienten nicht voneinander abhängen (dies wurde hier vorausgesetzt), |
*alle möglichen Amplitudenkoeffizienten gleichwahrscheinlich sind. | *alle möglichen Amplitudenkoeffizienten gleichwahrscheinlich sind. | ||
| − | In diesem Sinne ist $s_{0.5}(t)$ ein redundanzfreies Signal | + | In diesem Sinne ist $s_{0.5}(t)$ ein redundanzfreies Signal ⇒ <u>Lösungsvorschlag 2</u>. |
| + | *Somit ist hier die Entropie (der mittlere Informationsgehalt pro übertragenem Binärsymbol) maximal gleich dem Entscheidungsgehalt: | ||
:$$H_{\rm max} = {1}/{2}\cdot {\rm log}_2 (2)+{1}/{2}\cdot {\rm log}_2 (2) = 1 \,\,{\rm bit/Bin\ddot{a}rsymbol} \hspace{0.05cm}.$$ | :$$H_{\rm max} = {1}/{2}\cdot {\rm log}_2 (2)+{1}/{2}\cdot {\rm log}_2 (2) = 1 \,\,{\rm bit/Bin\ddot{a}rsymbol} \hspace{0.05cm}.$$ | ||
| − | Dagegen gilt für die Entropien der beiden anderen Binärsignale: | + | *Dagegen gilt für die Entropien der beiden anderen Binärsignale: |
:$$H = \ \frac{3}{4}\cdot {\rm log}_2 (\frac{4}{3})+ \frac{1}{4}\cdot {\rm log}_2 (4) | :$$H = \ \frac{3}{4}\cdot {\rm log}_2 (\frac{4}{3})+ \frac{1}{4}\cdot {\rm log}_2 (4) | ||
= \left( \frac{3}{4} + \frac{1}{4}\right)\cdot {\rm log}_2 (4) - | = \left( \frac{3}{4} + \frac{1}{4}\right)\cdot {\rm log}_2 (4) - | ||
| Zeile 104: | Zeile 104: | ||
:$$ \hspace{0.5cm} = \ 2 - \frac{3}{4}\cdot{\rm log}_2 (3) = | :$$ \hspace{0.5cm} = \ 2 - \frac{3}{4}\cdot{\rm log}_2 (3) = | ||
0.811 \,\,{\rm bit/Bin\ddot{a}rsymbol} \hspace{0.05cm}.$$ | 0.811 \,\,{\rm bit/Bin\ddot{a}rsymbol} \hspace{0.05cm}.$$ | ||
| − | Daraus ergibt sich für die relative Redundanz dieser Signale: | + | *Daraus ergibt sich für die relative Redundanz dieser Signale: |
:$$r = \frac{H_{\rm max} - H}{H_{\rm max}}\hspace{0.15cm} \approx 18.9\%\hspace{0.05cm}.$$ | :$$r = \frac{H_{\rm max} - H}{H_{\rm max}}\hspace{0.15cm} \approx 18.9\%\hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' Das zweite Moment ist unabhängig von $p$ gleich $m_{2a} = 1$: |
:$$m_{2a}={\rm E}[a_\nu^2] = p \cdot (+1)^2 + (1-p)\cdot (-1)^2 \hspace{0.15cm}\underline { = 1 \hspace{0.05cm}}.$$ | :$$m_{2a}={\rm E}[a_\nu^2] = p \cdot (+1)^2 + (1-p)\cdot (-1)^2 \hspace{0.15cm}\underline { = 1 \hspace{0.05cm}}.$$ | ||
| + | |||
'''(3)''' Für den linearen Mittelwert erhält man | '''(3)''' Für den linearen Mittelwert erhält man | ||
:$$m_{a}={\rm E}[a_\nu] = p \cdot (+1) + (1-p)\cdot (-1) = 2 p -1 \hspace{0.05cm}.$$ | :$$m_{a}={\rm E}[a_\nu] = p \cdot (+1) + (1-p)\cdot (-1) = 2 p -1 \hspace{0.05cm}.$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm} p = 0.75: m_{a}\hspace{0.15cm}\underline {=0.50},\hspace{0.2cm} p = 0.50: m_{a}\hspace{0.15cm}\underline {=0},\hspace{0.2cm} p = 0.25: m_{a}\hspace{0.15cm}\underline { =-0.50 \hspace{0.05cm}}.$$ | + | :$$\Rightarrow \hspace{0.3cm} p = 0.75\text{:} \hspace{0.4cm} m_{a}\hspace{0.15cm}\underline {=0.50},\hspace{0.2cm} p = 0.50\text{:} \hspace{0.4cm} m_{a}\hspace{0.15cm}\underline {=0},\hspace{0.2cm} p = 0.25\text{:} \hspace{0.4cm} m_{a}\hspace{0.15cm}\underline { =-0.50 \hspace{0.05cm}}.$$ |
| + | |||
| + | |||
| + | '''(4)''' Mit den Ergebnissen aus '''(2)''' und '''(4)''' erhält man: | ||
| + | :$$p = 0.75\text{:} \hspace{0.4cm} \sigma_{a}^2 \hspace{0.15cm}\underline {=0.75},$$ | ||
| + | :$$ p = 0.50\text{:} \hspace{0.4cm} \sigma_{a}^2\hspace{0.15cm} \underline { =1.00 \hspace{0.05cm}},$$ | ||
| + | :$$ p = 0.25\text{:} \hspace{0.4cm} \sigma_{a}^2 \hspace{0.15cm}\underline {=0.75}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[Datei:P_ID1311__Dig_A_2_2e.png|right|frame|AKF bei NRZ- und RZ-Impulsen und gleichen Symbolwahrscheinlichkeiten]] | ||
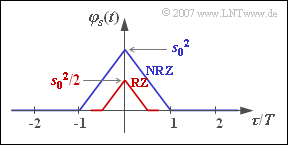
| + | '''(5)''' Richtig sind nur die <u>beiden ersten Aussagen</u>: | ||
| + | *Für $p = 0.5$ gilt $\varphi_{a}(\lambda = 0) = 1$ und $\varphi_{a}(\lambda \neq 0) = 0$. Daraus folgt: | ||
| + | $\varphi_s(\tau) = \frac{1}{T} \cdot \varphi^{^{\bullet}}_{gs}(\tau )\hspace{0.05cm}.$ | ||
| + | *Damit ergeben sich sowohl beim NRZ– als auch beim RZ–Grundimpuls eine dreieckförmige AKF und ein ${\rm si}^{2}$–förmiges LDS. | ||
| − | + | *Die Fläche unter dem LDS ist beim RZ–Impuls um den Faktor $T_{\rm S}/T$ kleiner als beim NRZ–Impuls, da sich auch die AKF–Werte bei $\tau = 0$ um diesen Faktor unterscheiden. | |
| − | + | *Das LDS ist in beiden Fällen kontinuierlich, da die AKF keinen Gleichanteil und keine periodischen Anteile beinhaltet. | |
| − | |||
| − | |||
| − | |||
| − | [[Datei:P_ID1330__Dig_A_2_2f.png|right|frame|AKF bei ungleichen Symbolwahrscheinlichkeiten]] | + | [[Datei:P_ID1330__Dig_A_2_2f.png|right|frame|AKF bei NRZ-Impulsen und ungleichen Symbolwahrscheinlichkeiten]] |
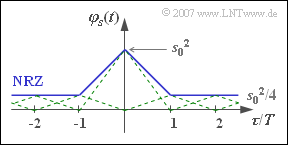
| − | '''(6)''' Für $p = 0.75$ setzt sich die AKF $\varphi_{s}(\tau)$ aus unendlich vielen Dreieckfunktionen zusammen, die mit Ausnahme des mittleren Dreiecks um $\tau = 0$ alle die gleiche Höhe $s_{0}^{2}/4$ aufweisen | + | '''(6)''' Richtig sind <u>alle Aussagen mit Ausnahme der dritten</u>: |
| + | *Für $p = 0.75$ setzt sich die AKF $\varphi_{s}(\tau)$ aus unendlich vielen Dreieckfunktionen zusammen, die mit Ausnahme des mittleren Dreiecks um $\tau = 0$ alle die gleiche Höhe $s_{0}^{2}/4$ aufweisen. | ||
| + | *Entsprechend der Skizze kann man alle diese Dreieckfunktionen zu einem Gleichanteil der Höhe $m_{a}^{2} \cdot s_{0}^{2} = s_{0}^{2}/4$ und einem einzigen Dreieck um $\tau = 0$ mit der Höhe $\sigma_{a}^{2} \cdot s_{0}^{2} = 3/4 · s_{0}^{2}$ zusammenfassen. | ||
| − | Im LDS führt dies zu einem kontinuierlichen | + | *Im LDS führt dies zu einem kontinuierlichen ${\rm si}^{2}$–förmigem Anteil und zu einer Diracfunktion bei $f = 0$. Das Gewicht dieses Diracs ist $s_{0}^{2}/4$. |
| + | *Für $p = 0.25$ ergibt sich die gleiche AKF wie mit $p = 0.75$, da sowohl die "Gesamtleistung" $m_{2a} = 1$ als auch die "Gleichleistung" $m_{a}^{2} = 0.25$ übereinstimmen. Somit stimmen natürlich auch die Leistungsdichtespektren überein. | ||
| − | |||
[[Datei:P_ID1331__Dig_A_2_2g.png|right|frame|AKF bei RZ-Rechteckimpulsen]] | [[Datei:P_ID1331__Dig_A_2_2g.png|right|frame|AKF bei RZ-Rechteckimpulsen]] | ||
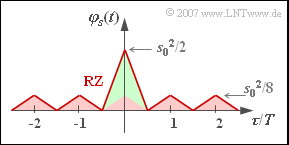
| − | '''(7)''' Mit dem RZ–Tastverhältnis $T_{\rm S}/T = 0.5$ ergibt sich die skizzierte AKF, die auch durch eine periodische Dreieckfunktion der Höhe $s_{0}^{2}/8$ (mit roter Füllung) und einem einzigen Dreieckimpuls der Höhe $3/8 \cdot s_{0}^{2}$ (grün gefüllt) dargestellt werden kann. Dieser nichtperiodische Anteil führt zu einem kontinuierlichen | + | '''(7)''' <u>Beide Lösungsvorschläge sind richtig</u>: |
| + | *Mit dem RZ–Tastverhältnis $T_{\rm S}/T = 0.5$ ergibt sich die skizzierte AKF, die auch durch eine periodische Dreieckfunktion der Höhe $s_{0}^{2}/8$ (mit roter Füllung) und einem einzigen Dreieckimpuls der Höhe $3/8 \cdot s_{0}^{2}$ (grün gefüllt) dargestellt werden kann. | ||
| + | |||
| + | *Dieser nichtperiodische Anteil führt zu einem kontinuierlichen ${\rm si}^{2}$–förmigen LDS mit Nullstellen bei Vielfachen von $2/T$. | ||
| + | |||
| + | *Die periodische Dreieck–AKF bewirkt im LDS Diracfunktionen bei Vielfachen von $1/T$. | ||
| + | |||
| + | *Aufgrund der Antimetrie des periodischen Anteils besitzen die Diracfunktionen bei Vielfachen von $2/T$ allerdings jeweils das Gewicht $0$. | ||
| + | |||
| + | *Die Gewichte der Diracfunktionen im Abstand $1/T$ sind proportional zum kontinuierlichen LDS–Anteil. | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 14. Mai 2022, 13:27 Uhr
Wir gehen von folgendem Signal aus:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$
Der Sendegrundimpuls $g_{s}(t)$ wird in dieser Aufgabe stets als rechteckförmig angenommen, wobei das NRZ–Format (blaue Signalverläufe in der Grafik) als auch das RZ–Format mit dem Tastverhältnis $T_{\rm S}/T = 0.5$ (rote Signalverläufe) zu untersuchen ist.
Die Amplitudenkoeffizienten besitzen die folgenden Eigenschaften:
- Sie sind binär und bipolar: $a_{\nu} \in \{–1, +1\}$.
- Die Symbole innerhalb der Folge $\langle a_{\nu }\rangle$ weisen keine statistischen Bindungen auf.
- Die Wahrscheinlichkeiten für die beiden möglichen Werte $±1$ lauten mit $0 < p < 1$:
- $${\rm Pr}(a_\nu = +1) \ = \ p,$$
- $${\rm Pr}(a_\nu = -1) \ = \ 1 - p \hspace{0.05cm}.$$
Die drei in der Grafik dargestellten Signalausschnitte gelten für $p = 0.75$, $p = 0.50$ und $p = 0.25$.
Im Laufe dieser Aufgabe wird auf folgende Beschreibungsgrößen Bezug genommen:
- $m_{a} = \E\big[a_{\nu}\big]$ gibt den linearen Mittelwert der Amplitudenkoeffizienten an.
- $m_{2a} = \E\big[a_{\nu}^{2}\big]$ ist das Moment zweiter Ordnung ("Leistung").
- Damit kann auch die Varianz $\sigma_{a}^{2} = m_{2a} - m_{a}^{2}$ berechnet werden.
- Die diskrete AKF der Amplitudenkoeffizienten ist $\varphi_{a}(\lambda) = \E\big[a_{\nu} \cdot a_{\nu} + \lambda \big]$. Es gilt hier:
- $$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 \\ m_1^2 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \hspace{0.05cm}.\\ \end{array}$$
- Die Energie–AKF des Sendegrundimpulses beträgt:
- $$\varphi^{^{\bullet}}_{g_s}(\tau) = \left\{ \begin{array}{c} s_0^2 \cdot T_{\rm S} \cdot \left( 1 - {|\tau|}/{T_{\rm S}}\right) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}|\tau| \le T_{\rm S} \\ |\tau| \ge T_{\rm S} \hspace{0.05cm}.\\ \end{array}$$
- Damit erhält man für die gesamte AKF des Sendesignals:
- $$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{g_s}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
- Das Leistungsdichtespektrum ${\it \Phi}_{s}(f)$ ist die Fouriertransformierte der AKF $\varphi_{s}(\tau)$.
Hinweis: Die Aufgabe gehört zum Kapitel "Grundlagen der codierten Übertragung".
Fragebogen
Musterlösung
- die Amplitudenkoeffizienten nicht voneinander abhängen (dies wurde hier vorausgesetzt),
- alle möglichen Amplitudenkoeffizienten gleichwahrscheinlich sind.
In diesem Sinne ist $s_{0.5}(t)$ ein redundanzfreies Signal ⇒ Lösungsvorschlag 2.
- Somit ist hier die Entropie (der mittlere Informationsgehalt pro übertragenem Binärsymbol) maximal gleich dem Entscheidungsgehalt:
- $$H_{\rm max} = {1}/{2}\cdot {\rm log}_2 (2)+{1}/{2}\cdot {\rm log}_2 (2) = 1 \,\,{\rm bit/Bin\ddot{a}rsymbol} \hspace{0.05cm}.$$
- Dagegen gilt für die Entropien der beiden anderen Binärsignale:
- $$H = \ \frac{3}{4}\cdot {\rm log}_2 (\frac{4}{3})+ \frac{1}{4}\cdot {\rm log}_2 (4) = \left( \frac{3}{4} + \frac{1}{4}\right)\cdot {\rm log}_2 (4) - \frac{3}{4}\cdot{\rm log}_2 (3) =$$
- $$ \hspace{0.5cm} = \ 2 - \frac{3}{4}\cdot{\rm log}_2 (3) = 0.811 \,\,{\rm bit/Bin\ddot{a}rsymbol} \hspace{0.05cm}.$$
- Daraus ergibt sich für die relative Redundanz dieser Signale:
- $$r = \frac{H_{\rm max} - H}{H_{\rm max}}\hspace{0.15cm} \approx 18.9\%\hspace{0.05cm}.$$
(2) Das zweite Moment ist unabhängig von $p$ gleich $m_{2a} = 1$:
- $$m_{2a}={\rm E}[a_\nu^2] = p \cdot (+1)^2 + (1-p)\cdot (-1)^2 \hspace{0.15cm}\underline { = 1 \hspace{0.05cm}}.$$
(3) Für den linearen Mittelwert erhält man
- $$m_{a}={\rm E}[a_\nu] = p \cdot (+1) + (1-p)\cdot (-1) = 2 p -1 \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm} p = 0.75\text{:} \hspace{0.4cm} m_{a}\hspace{0.15cm}\underline {=0.50},\hspace{0.2cm} p = 0.50\text{:} \hspace{0.4cm} m_{a}\hspace{0.15cm}\underline {=0},\hspace{0.2cm} p = 0.25\text{:} \hspace{0.4cm} m_{a}\hspace{0.15cm}\underline { =-0.50 \hspace{0.05cm}}.$$
(4) Mit den Ergebnissen aus (2) und (4) erhält man:
- $$p = 0.75\text{:} \hspace{0.4cm} \sigma_{a}^2 \hspace{0.15cm}\underline {=0.75},$$
- $$ p = 0.50\text{:} \hspace{0.4cm} \sigma_{a}^2\hspace{0.15cm} \underline { =1.00 \hspace{0.05cm}},$$
- $$ p = 0.25\text{:} \hspace{0.4cm} \sigma_{a}^2 \hspace{0.15cm}\underline {=0.75}.$$
(5) Richtig sind nur die beiden ersten Aussagen:
- Für $p = 0.5$ gilt $\varphi_{a}(\lambda = 0) = 1$ und $\varphi_{a}(\lambda \neq 0) = 0$. Daraus folgt:
$\varphi_s(\tau) = \frac{1}{T} \cdot \varphi^{^{\bullet}}_{gs}(\tau )\hspace{0.05cm}.$
- Damit ergeben sich sowohl beim NRZ– als auch beim RZ–Grundimpuls eine dreieckförmige AKF und ein ${\rm si}^{2}$–förmiges LDS.
- Die Fläche unter dem LDS ist beim RZ–Impuls um den Faktor $T_{\rm S}/T$ kleiner als beim NRZ–Impuls, da sich auch die AKF–Werte bei $\tau = 0$ um diesen Faktor unterscheiden.
- Das LDS ist in beiden Fällen kontinuierlich, da die AKF keinen Gleichanteil und keine periodischen Anteile beinhaltet.
(6) Richtig sind alle Aussagen mit Ausnahme der dritten:
- Für $p = 0.75$ setzt sich die AKF $\varphi_{s}(\tau)$ aus unendlich vielen Dreieckfunktionen zusammen, die mit Ausnahme des mittleren Dreiecks um $\tau = 0$ alle die gleiche Höhe $s_{0}^{2}/4$ aufweisen.
- Entsprechend der Skizze kann man alle diese Dreieckfunktionen zu einem Gleichanteil der Höhe $m_{a}^{2} \cdot s_{0}^{2} = s_{0}^{2}/4$ und einem einzigen Dreieck um $\tau = 0$ mit der Höhe $\sigma_{a}^{2} \cdot s_{0}^{2} = 3/4 · s_{0}^{2}$ zusammenfassen.
- Im LDS führt dies zu einem kontinuierlichen ${\rm si}^{2}$–förmigem Anteil und zu einer Diracfunktion bei $f = 0$. Das Gewicht dieses Diracs ist $s_{0}^{2}/4$.
- Für $p = 0.25$ ergibt sich die gleiche AKF wie mit $p = 0.75$, da sowohl die "Gesamtleistung" $m_{2a} = 1$ als auch die "Gleichleistung" $m_{a}^{2} = 0.25$ übereinstimmen. Somit stimmen natürlich auch die Leistungsdichtespektren überein.
(7) Beide Lösungsvorschläge sind richtig:
- Mit dem RZ–Tastverhältnis $T_{\rm S}/T = 0.5$ ergibt sich die skizzierte AKF, die auch durch eine periodische Dreieckfunktion der Höhe $s_{0}^{2}/8$ (mit roter Füllung) und einem einzigen Dreieckimpuls der Höhe $3/8 \cdot s_{0}^{2}$ (grün gefüllt) dargestellt werden kann.
- Dieser nichtperiodische Anteil führt zu einem kontinuierlichen ${\rm si}^{2}$–förmigen LDS mit Nullstellen bei Vielfachen von $2/T$.
- Die periodische Dreieck–AKF bewirkt im LDS Diracfunktionen bei Vielfachen von $1/T$.
- Aufgrund der Antimetrie des periodischen Anteils besitzen die Diracfunktionen bei Vielfachen von $2/T$ allerdings jeweils das Gewicht $0$.
- Die Gewichte der Diracfunktionen im Abstand $1/T$ sind proportional zum kontinuierlichen LDS–Anteil.