Aufgaben:Aufgabe 1.09Z: Erweiterung und/oder Punktierung: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Allgemeine Beschreibung linearer Blockcodes }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-C…“) |
|||
| (21 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Allgemeine Beschreibung linearer Blockcodes | + | {{quiz-Header|Buchseite=Kanalcodierung/Allgemeine Beschreibung linearer Blockcodes}} |
| − | }} | + | [[Datei:P_ID2403__KC_Z_1_9.png|right|frame|Zur Erweiterung und Punktierung]] |
| + | |||
| + | Häufig kennt man einen Code, der für eine Anwendung als geeignet erscheint, dessen Coderate aber nicht exakt mit den Vorgaben übereinstimmt. | ||
| + | |||
| + | Zur Ratenanpassung gibt es verschiedene Möglichkeiten | ||
| + | |||
| + | '''Erweiterung''' (englisch: "Extension"): | ||
| + | <br>Ausgehend vom $(n, \, k)$–Code, dessen Prüfmatrix $\mathbf{H}$ gegeben ist, erhält man einen $(n+1, \, k)$–Code, indem man die Prüfmatrix um eine Zeile und eine Spalte erweitert und die neuen Matrixelemente entsprechend der oberen Grafik mit Nullen und Einsen ergänzt. Man fügt ein neues Prüfbit | ||
| + | :$$x_{n+1} = x_1 \oplus x_2 \oplus ... \hspace{0.05cm} \oplus x_n$$ | ||
| + | hinzu und damit auch eine neue Prüfgleichung, die in $\mathbf{H}\hspace{0.05cm}'$ berücksichtigt ist. | ||
| + | |||
| + | '''Punktierung''' (englisch: "Puncturing"): | ||
| + | <br>Entsprechend der unteren Abbildung kommt man zu einem $(n-1, \, k)$–Code größerer Rate, wenn man auf ein Prüfbit und eine Prüfgleichung verzichtet, was gleichbedeutend damit ist, aus der Prüfmatrix $\mathbf{H}$ eine Zeile und eine Spalte zu streichen. | ||
| + | |||
| + | '''Verkürzung''' (englisch: "Shortening"): | ||
| + | <br>Verzichtet man anstelle eines Prüfbits auf ein Informationsbit, so ergibt sich ein $(n-1, \, k-1)$–Code kleinerer Rate. | ||
| + | |||
| + | |||
| + | In dieser Aufgabe sollen ausgehend von einem $(5, \, 2)$–Blockcode | ||
| + | |||
| + | :$$\mathcal{C} = \{ (0, 0, 0, 0, 0), \hspace{0.3cm} (0, 1, 0, 1, 1), \hspace{0.3cm}(1, 0, 1, 1, 0), \hspace{0.3cm}(1, 1, 1, 0, 1) \}$$ | ||
| + | |||
| + | folgende Codes konstruiert und analysiert werden: | ||
| + | *ein $(6, \, 2)$–Code durch einmalige Erweiterung, | ||
| + | |||
| + | *ein $(7, \, 2)$–Code durch nochmalige Erweiterung, | ||
| + | |||
| + | *ein $(4, \, 2)$–Code durch Punktierung. | ||
| + | |||
| + | |||
| + | Die Prüfmatrix und die Generatormatrix des systematischen $(5, \, 2)$–Codes lauten: | ||
| + | |||
| + | :$${ \boldsymbol{\rm H}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.3cm} \Leftrightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | |||
| + | *Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes|"Allgemeine Beschreibung linearer Blockcodes"]]. | ||
| + | |||
| + | * In der [[Aufgaben:Aufgabe_1.09:_Erweiterter_Hamming–Code|"Aufgabe 1.9"]] wird beispielhaft gezeigt, wie aus dem $(7, \, 4, \, 3)$–Hamming–Code durch Erweiterung ein $(8, \, 4, \, 4)$–Code entsteht. | ||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| + | <quiz display=simple> | ||
| + | {Geben Sie die Kenngrößen des vorgegebenen $(5, \, 2)$–Codes an. | ||
| + | |type="{}"} | ||
| + | $R \ = \ $ { 0.4 3% } | ||
| + | $d_{\rm min} \ = \ $ { 3 3% } | ||
| − | + | {Welche Codeworte besitzt der $(6, \, 2)$–Code nach Erweiterung? | |
| − | { | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - $(0 0 0 0 0 1), \ (0 1 0 1 1 0), \ (1 0 1 1 0 0), \ (1 1 1 0 1 1).$ |
| − | + | + | + $(0 0 0 0 0 0), \ (0 1 0 1 1 1), \ (1 0 1 1 0 1), \ (1 1 1 0 1 0).$ |
| − | |||
| − | { | + | {Geben Sie die Kenngrößen des erweiterten $(6, \, 2)$–Codes an. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $R \ = \ $ { 0.333 3% } |
| + | $d_{\rm min} \ = \ $ { 4 3% } | ||
| + | {Wie lautet die systematische Generatormatrix $\boldsymbol{\rm G}$ des $(7, \, 2)$–Codes? | ||
| + | |type="[]"} | ||
| + | + Zeile 1 von $\boldsymbol{\rm G} \text{:} \hspace{0.2cm} 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, 0.$ | ||
| + | + Zeile 2 von $\boldsymbol{\rm G} \text{:} \hspace{0.2cm} 0, \, 1, \, 0, \, 1, \, 1, \, 1, \, 0.$ | ||
| + | {Geben Sie die Kenngrößen des erweiterten $(7, \, 2)$–Codes an. | ||
| + | |type="{}"} | ||
| + | $R \ = \ $ { 0.266 3% } | ||
| + | $d_{\rm min} \ = \ $ { 4 3% } | ||
| + | {Welche Aussagen gelten für den $(4, \, 2)$–Code (Punktierung des letzten Prüfbits)? | ||
| + | |type="[]"} | ||
| + | + Die Coderate beträgt nun $R = 2/4 = 0.5$. | ||
| + | + $C_{(4, 2)} = \{(0, 0, 0, 0), \, (1, 0, 1, 1), \, (0, 1, 0, 1), \, (1, 1, 1, 0)\}$. | ||
| + | - Die Minimaldistanz bleibt gegenüber dem $(5, \, 2)$–Code unverändert. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Die Rate des $(5, \, 2)$–Codes ist $R = 2/5 \ \underline{ = 0.4}$. |
| − | '''2 | + | *Aus dem angegebenen Code erkennt man weiterhin die minimale Distanz $d_{\rm min} \ \underline{ = 3}$. |
| − | '''3 | + | |
| − | '''4 | + | |
| − | ''' | + | |
| − | ''' | + | '''(2)''' Bei Erweiterung vom $(5, \, 2)$–Code zum $(6, \, 2)$–Code wird ein weiteres Prüfbit hinzugefügt. |
| − | ''' | + | *Das Codewort hat somit die Form |
| + | |||
| + | :$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6) = ( u_1, u_2, p_1, p_2, p_{3}, p_4) \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Für das hinzugekommene Prüfbit muss dabei gelten: | ||
| + | |||
| + | :$$p_4 = x_6 = x_1 \oplus x_2 \oplus x_3 \oplus x_4 \oplus x_5 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Das heißt: Das neue Prüfbit $p_{4}$ wird so gewählt, dass sich in jedem Codewort eine gerade Anzahl von Einsen ergibt ⇒ <u>Antwort 2</u>. | ||
| + | |||
| + | *Löst man diese Aufgabe mit der Prüfmatrix, so erhält man | ||
| + | :$${ \boldsymbol{\rm H}}_{(6,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &0 &0 &0 &1 \end{pmatrix}\hspace{0.3cm} | ||
| + | \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &1 &0 &1\\ 0 &1 &0 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Die beiden Zeilen der Generatormatrix $\boldsymbol{\rm G}$ ergeben zwei der vier Codeworte, die Modulo–$2$–Summe das dritte und schließlich ist auch noch das Nullwort zu berücksichtigen. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Nach Erweiterung vom $(5, \, 2)$–Code auf den $(6, \, 2)$–Code | ||
| + | *vermindert sich die Rate von $R = 2/5$ auf $R = 2/6 \ \underline{= 0.333}$, | ||
| + | |||
| + | *erhöht sich die Minimaldistanz von $d_{\rm min} = 3$ auf $d_{\rm min} \ \underline{= 4}$ . | ||
| + | |||
| + | |||
| + | <u>Allgemein gilt:</u> Erweitert man einen Code, so nimmt die Rate ab und die Minimaldistanz erhöht sich um $1$, falls $d_{\rm min}$ vorher ungerade war. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Bei gleicher Vorgehensweise wie unter '''(3)''' erhält man | ||
| + | :$${ \boldsymbol{\rm H}}_{(7,\hspace{0.05cm} 2)} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &0 &0 &0 &0\\ 1 &1 &0 &1 &0 &0 &0\\ 0 &1 &0 &0 &1 &0 &0\\ 1 &1 &0 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.15cm} \Rightarrow\hspace{0.15cm} { \boldsymbol{\rm H}}_{{\rm (7,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &0 &0 &0 &0\\ 1 &1 &0 &1 &0 &0 &0\\ 0 &1 &0 &0 &1 &0 &0\\ 1 &1 &0 &0 &0 &1 &0\\ 0 &0 &0 &0 &0 &0 &1 \end{pmatrix}\hspace{0.15cm} \Rightarrow\hspace{0.15cm} { \boldsymbol{\rm G}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &1 &0 &1 &0 \\ 0 &1 &0 &1 &1 &1 &0 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| + | |||
| + | ⇒ <u>Beide Antworten</u> sind richtig. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Die Rate beträgt nun $R = 2/7 = \underline{0.266}$. | ||
| + | *Die Minimaldistanz ist weiterhin $d_{\rm min} \ \underline{= 4}$, wie man aus den $(7, \, 2)$–Codeworten ablesen kann: | ||
| + | :$$\mathcal{C} = \{ (0, 0, 0, 0, 0, 0, 0), \hspace{0.3cm}(0, 1, 0, 1, 1, 1, 0), \hspace{0.3cm}(1, 0, 1, 1, 0, 1, 0), \hspace{0.3cm}(1, 1, 1, 0, 1, 0, 0) \}\hspace{0.05cm}.$$ | ||
| + | |||
| + | <u>Allgemein gilt:</u> Ist die Minimaldistanz eines Codes geradzahlig, so kann diese durch Erweiterung nicht vergrößert werden. | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Richtig sind die <u>Aussagen 1 und 2</u>: | ||
| + | *Durch Streichen der letzten Zeile und der letzten Spalte erhält man für Prüfmatrix bzw. Generatormatrix (jeweils in systematischer Form): | ||
| + | :$${ \boldsymbol{\rm H}}_{(4,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 \\ 1 &1 &0 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (4,\hspace{0.05cm} 2)}} = \begin{pmatrix} 1 &0 &1 &1 \\ 0 &1 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Aus der Generatormatrix ergeben sich die genannten Codeworte $(1, 0, 1, 1), \, (0, 1, 0, 1), \, (1, 1, 1, 0)$ als Zeilensumme sowie das Nullwort $(0, 0, 0, 0)$. Die Minimaldistanz dieses Codes ist $d_{\rm min}= 2$ und damit kleiner als die minimale Distanz $d_{\rm min}= 3$ des $(5, \, 2)$–Codes. | ||
| + | |||
| + | |||
| + | <u>Allgemein gilt:</u> Durch Punktierung wird $d_{\rm min}$ um $1$ kleiner (wenn sie vorher gerade war) oder sie bleibt gleich. Dies kann man sich verdeutlichen, wenn man durch eine weitere Punktierung $($des Prüfbits $p_{2})$ den $(3, \, 2)$–Blockcode generiert. Dieser Code | ||
| + | :$$ \mathcal{C} = \{ (0, 0, 0), \hspace{0.1cm}(0, 1, 1), \hspace{0.3cm}(1, 0, 1), \hspace{0.3cm}(1, 1, 0) \}$$ | ||
| + | besitzt die gleiche Minimaldistanz $d_{\rm min}= 2$ wie der $(4, \, 2)$–Code. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Kanalcodierung|^1.4 | + | [[Category:Aufgaben zu Kanalcodierung|^1.4 Beschreibung linearer Blockcodes^]] |
| − | |||
| − | ^]] | ||
Aktuelle Version vom 12. Juli 2022, 11:52 Uhr
Häufig kennt man einen Code, der für eine Anwendung als geeignet erscheint, dessen Coderate aber nicht exakt mit den Vorgaben übereinstimmt.
Zur Ratenanpassung gibt es verschiedene Möglichkeiten
Erweiterung (englisch: "Extension"):
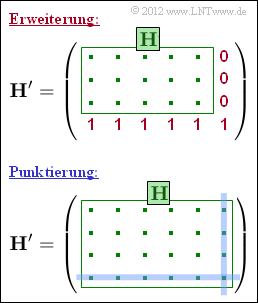
Ausgehend vom $(n, \, k)$–Code, dessen Prüfmatrix $\mathbf{H}$ gegeben ist, erhält man einen $(n+1, \, k)$–Code, indem man die Prüfmatrix um eine Zeile und eine Spalte erweitert und die neuen Matrixelemente entsprechend der oberen Grafik mit Nullen und Einsen ergänzt. Man fügt ein neues Prüfbit
- $$x_{n+1} = x_1 \oplus x_2 \oplus ... \hspace{0.05cm} \oplus x_n$$
hinzu und damit auch eine neue Prüfgleichung, die in $\mathbf{H}\hspace{0.05cm}'$ berücksichtigt ist.
Punktierung (englisch: "Puncturing"):
Entsprechend der unteren Abbildung kommt man zu einem $(n-1, \, k)$–Code größerer Rate, wenn man auf ein Prüfbit und eine Prüfgleichung verzichtet, was gleichbedeutend damit ist, aus der Prüfmatrix $\mathbf{H}$ eine Zeile und eine Spalte zu streichen.
Verkürzung (englisch: "Shortening"):
Verzichtet man anstelle eines Prüfbits auf ein Informationsbit, so ergibt sich ein $(n-1, \, k-1)$–Code kleinerer Rate.
In dieser Aufgabe sollen ausgehend von einem $(5, \, 2)$–Blockcode
- $$\mathcal{C} = \{ (0, 0, 0, 0, 0), \hspace{0.3cm} (0, 1, 0, 1, 1), \hspace{0.3cm}(1, 0, 1, 1, 0), \hspace{0.3cm}(1, 1, 1, 0, 1) \}$$
folgende Codes konstruiert und analysiert werden:
- ein $(6, \, 2)$–Code durch einmalige Erweiterung,
- ein $(7, \, 2)$–Code durch nochmalige Erweiterung,
- ein $(4, \, 2)$–Code durch Punktierung.
Die Prüfmatrix und die Generatormatrix des systematischen $(5, \, 2)$–Codes lauten:
- $${ \boldsymbol{\rm H}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.3cm} \Leftrightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Allgemeine Beschreibung linearer Blockcodes".
- In der "Aufgabe 1.9" wird beispielhaft gezeigt, wie aus dem $(7, \, 4, \, 3)$–Hamming–Code durch Erweiterung ein $(8, \, 4, \, 4)$–Code entsteht.
Fragebogen
Musterlösung
- Aus dem angegebenen Code erkennt man weiterhin die minimale Distanz $d_{\rm min} \ \underline{ = 3}$.
(2) Bei Erweiterung vom $(5, \, 2)$–Code zum $(6, \, 2)$–Code wird ein weiteres Prüfbit hinzugefügt.
- Das Codewort hat somit die Form
- $$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6) = ( u_1, u_2, p_1, p_2, p_{3}, p_4) \hspace{0.05cm}.$$
- Für das hinzugekommene Prüfbit muss dabei gelten:
- $$p_4 = x_6 = x_1 \oplus x_2 \oplus x_3 \oplus x_4 \oplus x_5 \hspace{0.05cm}.$$
- Das heißt: Das neue Prüfbit $p_{4}$ wird so gewählt, dass sich in jedem Codewort eine gerade Anzahl von Einsen ergibt ⇒ Antwort 2.
- Löst man diese Aufgabe mit der Prüfmatrix, so erhält man
- $${ \boldsymbol{\rm H}}_{(6,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &0 &0 &0 &1 \end{pmatrix}\hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &1 &0 &1\\ 0 &1 &0 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$
- Die beiden Zeilen der Generatormatrix $\boldsymbol{\rm G}$ ergeben zwei der vier Codeworte, die Modulo–$2$–Summe das dritte und schließlich ist auch noch das Nullwort zu berücksichtigen.
(3) Nach Erweiterung vom $(5, \, 2)$–Code auf den $(6, \, 2)$–Code
- vermindert sich die Rate von $R = 2/5$ auf $R = 2/6 \ \underline{= 0.333}$,
- erhöht sich die Minimaldistanz von $d_{\rm min} = 3$ auf $d_{\rm min} \ \underline{= 4}$ .
Allgemein gilt: Erweitert man einen Code, so nimmt die Rate ab und die Minimaldistanz erhöht sich um $1$, falls $d_{\rm min}$ vorher ungerade war.
(4) Bei gleicher Vorgehensweise wie unter (3) erhält man
- $${ \boldsymbol{\rm H}}_{(7,\hspace{0.05cm} 2)} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &0 &0 &0 &0\\ 1 &1 &0 &1 &0 &0 &0\\ 0 &1 &0 &0 &1 &0 &0\\ 1 &1 &0 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.15cm} \Rightarrow\hspace{0.15cm} { \boldsymbol{\rm H}}_{{\rm (7,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &0 &0 &0 &0\\ 1 &1 &0 &1 &0 &0 &0\\ 0 &1 &0 &0 &1 &0 &0\\ 1 &1 &0 &0 &0 &1 &0\\ 0 &0 &0 &0 &0 &0 &1 \end{pmatrix}\hspace{0.15cm} \Rightarrow\hspace{0.15cm} { \boldsymbol{\rm G}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &1 &0 &1 &0 \\ 0 &1 &0 &1 &1 &1 &0 \end{pmatrix}\hspace{0.05cm}.$$
⇒ Beide Antworten sind richtig.
(5) Die Rate beträgt nun $R = 2/7 = \underline{0.266}$.
- Die Minimaldistanz ist weiterhin $d_{\rm min} \ \underline{= 4}$, wie man aus den $(7, \, 2)$–Codeworten ablesen kann:
- $$\mathcal{C} = \{ (0, 0, 0, 0, 0, 0, 0), \hspace{0.3cm}(0, 1, 0, 1, 1, 1, 0), \hspace{0.3cm}(1, 0, 1, 1, 0, 1, 0), \hspace{0.3cm}(1, 1, 1, 0, 1, 0, 0) \}\hspace{0.05cm}.$$
Allgemein gilt: Ist die Minimaldistanz eines Codes geradzahlig, so kann diese durch Erweiterung nicht vergrößert werden.
(6) Richtig sind die Aussagen 1 und 2:
- Durch Streichen der letzten Zeile und der letzten Spalte erhält man für Prüfmatrix bzw. Generatormatrix (jeweils in systematischer Form):
- $${ \boldsymbol{\rm H}}_{(4,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 \\ 1 &1 &0 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (4,\hspace{0.05cm} 2)}} = \begin{pmatrix} 1 &0 &1 &1 \\ 0 &1 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$
- Aus der Generatormatrix ergeben sich die genannten Codeworte $(1, 0, 1, 1), \, (0, 1, 0, 1), \, (1, 1, 1, 0)$ als Zeilensumme sowie das Nullwort $(0, 0, 0, 0)$. Die Minimaldistanz dieses Codes ist $d_{\rm min}= 2$ und damit kleiner als die minimale Distanz $d_{\rm min}= 3$ des $(5, \, 2)$–Codes.
Allgemein gilt: Durch Punktierung wird $d_{\rm min}$ um $1$ kleiner (wenn sie vorher gerade war) oder sie bleibt gleich. Dies kann man sich verdeutlichen, wenn man durch eine weitere Punktierung $($des Prüfbits $p_{2})$ den $(3, \, 2)$–Blockcode generiert. Dieser Code
- $$ \mathcal{C} = \{ (0, 0, 0), \hspace{0.1cm}(0, 1, 1), \hspace{0.3cm}(1, 0, 1), \hspace{0.3cm}(1, 1, 0) \}$$
besitzt die gleiche Minimaldistanz $d_{\rm min}= 2$ wie der $(4, \, 2)$–Code.