Signaldarstellung/Prinzip der Nachrichtenübertragung: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 42: | Zeile 42: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Bitte beachten Sie:}$ | $\text{Bitte beachten Sie:}$ | ||
| − | *Die zur | + | *Die zur $\text{Nachrichtenübertragung}$ verwendeten Signale sind in der Regel Zeitfunktionen. Das bedeutet, dass (zumindest) einer der Signalparameter abhängig vom Zeitparameter $t$ ist. Solche Signalparameter sind beispielsweise bei einem Signalton die Amplitude („Lautstärke“) und die Frequenz („Tonhöhe“). |
| − | *In einem | + | *In einem $\text{Nachrichtenspeicher}$ werden die Zeitfunktionen oft auch auf räumliche Funktionen geeigneter physikalischer Größen wie Magnetisierung (Magnetband) oder Schwärzungsgrad (Film) abgebildet.}} |
| Zeile 82: | Zeile 82: | ||
| − | Wir bedanken uns bei ''Markus Kaindl'' <ref>Kaindl, M.: Kanalcodierung für Sprache und Daten in GSM-Systemen. Dissertation. Lehrstuhl für Nachrichtentechnik, TU München. VDI Fortschritt-Berichte, Reihe 10, Nr. 764, 2005.</ref>, LNT/TUM, für die Bereitstellung der Grafik.}} | + | Wir bedanken uns bei ''Markus Kaindl'' <ref>Kaindl, M.: Kanalcodierung für Sprache und Daten in GSM-Systemen.<br> Dissertation. Lehrstuhl für Nachrichtentechnik, TU München. VDI Fortschritt-Berichte, Reihe 10, Nr. 764, 2005.</ref>, LNT/TUM, für die Bereitstellung der Grafik.}} |
| Zeile 161: | Zeile 161: | ||
Entsprechende '''Funktionseinheiten''' des Empfängers sind: | Entsprechende '''Funktionseinheiten''' des Empfängers sind: | ||
| − | *Wandler – zum Beispiel ein Lautsprecher zur Umwandlung eines elektrischen in ein akustisches Signal (Gegenstück zum Mikrofon), | + | *Wandler – zum Beispiel ein Lautsprecher zur Umwandlung eines elektrischen in ein akustisches Signal $($Gegenstück zum Mikrofon$)$, |
| − | *Demodulation – zum Beispiel Frequenzrücksetzung des Signals in den ursprünglichen Frequenzbereich (Gegenstück zum AM/FM/PM | + | *Demodulation – zum Beispiel Frequenzrücksetzung des Signals in den ursprünglichen Frequenzbereich $($Gegenstück zum AM/FM/PM–Modulator$)$, |
| − | *Signalrücksetzung – zum Beispiel die Rekonstruktion des Analogsignals aus den digitalen Abtastwerten (D/A | + | *Signalrücksetzung – zum Beispiel die Rekonstruktion des Analogsignals aus den digitalen Abtastwerten $($D/A–Wandler ⇒ Gegenstück zum A/D-Wandler$)$, |
| − | *Decodierung – zum Beispiel mit der Möglichkeit zur Fehlererkennung und Fehlerkorrektur (Gegenstück zum Kanalcodierer). | + | *Decodierung – zum Beispiel mit der Möglichkeit zur Fehlererkennung und Fehlerkorrektur $($Gegenstück zum Kanalcodierer$)$. |
| Zeile 170: | Zeile 170: | ||
Eine weitere wichtige Aufgabe des Empfängers besteht darin, die bei der Übertragung aufgetretenen Signalverfälschungen und Störungen möglichst gut zu beseitigen. | Eine weitere wichtige Aufgabe des Empfängers besteht darin, die bei der Übertragung aufgetretenen Signalverfälschungen und Störungen möglichst gut zu beseitigen. | ||
| − | Die Realisierung solcher Systemkomponenten für Sender und Empfänger geschieht durch verschiedene elektrische Netzwerke und Baugruppen. Auch hier lassen sich beispielhaft einige Funktionseinheiten nennen: | + | Die Realisierung solcher Systemkomponenten für Sender und Empfänger geschieht durch verschiedene elektrische Netzwerke und Baugruppen. |
| + | |||
| + | Auch hier lassen sich beispielhaft einige Funktionseinheiten nennen: | ||
*Verstärker, Filter und Entzerrer, | *Verstärker, Filter und Entzerrer, | ||
*Oszillatoren und nichtlineare Komponenten zur (De-)Modulation und Synchronisation, | *Oszillatoren und nichtlineare Komponenten zur (De-)Modulation und Synchronisation, | ||
| Zeile 179: | Zeile 181: | ||
==Signalverfälschungen== | ==Signalverfälschungen== | ||
<br> | <br> | ||
| − | Es wurde bereits angesprochen, dass im Idealfall $v(t) = q(t)$ sein sollte. Gilt jedoch wie bei jedem realen Übertragungskanal $r(t) \neq s(t)$, so wird sich natürlich auch das Sinkensignal $v(t)$ vom Quellensignal $q(t)$ unterscheiden. Hierzu einige Beispiele: | + | Es wurde bereits angesprochen, dass im Idealfall $v(t) = q(t)$ sein sollte. Gilt jedoch wie bei jedem realen Übertragungskanal $r(t) \neq s(t)$, so wird sich natürlich auch das Sinkensignal $v(t)$ vom Quellensignal $q(t)$ unterscheiden. Hierzu einige Beispiele: |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Man spricht von '''Rauschen''', wenn für das Sinkensignal gilt: | + | $\text{Definition:}$ Man spricht von »'''Rauschen'''«, wenn für das Sinkensignal gilt: |
:: <math> v(t)=q(t)+n(t).</math> | :: <math> v(t)=q(t)+n(t).</math> | ||
| − | Der additive Rauschanteil $n(t)$ ist stets von stochastischer Natur und hat meist keinerlei Bezug zum Nachrichtensignal $q(t)$. Ein solcher Rauschterm ist bei jeder Übertragung unvermeidlich.}} | + | Der additive Rauschanteil $n(t)$ ist stets von stochastischer Natur und hat meist keinerlei Bezug zum Nachrichtensignal $q(t)$. Ein solcher Rauschterm ist bei jeder Übertragung unvermeidlich. Ist $n(t)$ extrem klein, so spricht man von „quasi–rauschfreier” Übertragung.}} |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Die Übertragung ist '''verzerrungsfrei''', wenn das Sinkensignal wie folgt lautet: | + | $\text{Definition:}$ Die Übertragung ist »'''verzerrungsfrei'''«, wenn das Sinkensignal wie folgt lautet: |
| − | :: <math>v(t)= | + | :: <math>v(t)=\alpha \cdot q(t-\tau)+n(t).</math> |
| − | Das Sinkensignal unterscheidet sich in diesem Falll vom Quellensignal – außer durch den Störanteil $n(t)$ – nur noch durch den (für alle Frequenzen gleichen) Dämpfungsfaktor $\alpha$ und die (ebenfalls für alle Frequenzen gleiche) Laufzeit $\tau$.}} | + | Das Sinkensignal unterscheidet sich in diesem Falll vom Quellensignal – außer durch den Störanteil $n(t)$ – nur noch durch den $($für alle Frequenzen gleichen$)$ Dämpfungsfaktor $\alpha$ und die $($ebenfalls für alle Frequenzen gleiche$)$ Laufzeit $\tau$.}} |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Ist die Gleichung $v(t)= | + | $\text{Definition:}$ Ist die Gleichung $v(t)=\alpha \cdot q(t-\tau)+n(t)$ nicht erfüllt, so liegen »'''Verzerrungen'''« vor. |
| + | |||
| + | Wie im Buch [[Lineare zeitinvariante Systeme]] beschrieben wird, unterscheidet man zwischen | ||
* [[Lineare_zeitinvariante_Systeme/Lineare_Verzerrungen|linearen Verzerrungen]] und | * [[Lineare_zeitinvariante_Systeme/Lineare_Verzerrungen|linearen Verzerrungen]] und | ||
* [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|nichtlinearen Verzerrungen]], | * [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|nichtlinearen Verzerrungen]], | ||
| − | + | Wir verweisen in diesem Zusammenhang auf das Lernvideo [[Lineare_und_nichtlineare_Verzerrungen_(Lernvideo)|»Lineare und nichtlineare Verzerrungen«]].}} | |
| − | |||
| − | |||
Hier nochmals in etwas anderen Worten: | Hier nochmals in etwas anderen Worten: | ||
| − | *Der Dämpfungsfaktor $\alpha$ bewirkt nur, dass das Signal $v(t)$ etwas „leiser“ ist als $q(t)$; beide Signale haben aber die gleiche Form. | + | *Der Dämpfungsfaktor $\alpha$ bewirkt nur, dass das Signal $v(t)$ etwas „leiser“ ist als $q(t)$; beide Signale haben aber die gleiche Form. |
| + | |||
*Die Laufzeit $\tau$ führt dazu, dass das Signal $v(t)$ am Empfänger später ankommt, als $q(t)$ gesendet wurde. | *Die Laufzeit $\tau$ führt dazu, dass das Signal $v(t)$ am Empfänger später ankommt, als $q(t)$ gesendet wurde. | ||
| − | Beide Effekte sind für eine | + | Beide Effekte sind für eine <u>unidirektionale Übertragung</u> nicht sonderlich störend: <br> Man kann zum Beispiel immer noch von einer Live-Übertragung sprechen, wenn das Fernsehbild um (Bruchteille von) Sekunden verzögert ankommt. |
| + | |||
| + | Bei einer <u>bidirektionalen Übertragung</u> kann eine zu lange Laufzeit allerdings zu Problemen führen:<br> Bei einem Telefonat fallen sich dann die beiden Gesprächspartner gegenseitig ins Wort. | ||
| − | |||
| − | |||
[[Datei:P_ID587_Sig_T_1_1_S7a.jpg|right|frame|Farbschablone zur Verdeutlichung von Verzerrungen und Rauschen]] | [[Datei:P_ID587_Sig_T_1_1_S7a.jpg|right|frame|Farbschablone zur Verdeutlichung von Verzerrungen und Rauschen]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| Zeile 227: | Zeile 230: | ||
| − | [[Datei:P_ID588_Sig_T_1_1_S7b.jpg|center|frame|Auswirkungen von Rauschen und Verzerrungen auf ein Bildsignal]] }} | + | [[Datei:P_ID588_Sig_T_1_1_S7b.jpg|center|frame|Auswirkungen von Rauschen und Verzerrungen auf ein Bildsignal]] }} |
| + | |||
| + | |||
Aktuelle Version vom 6. Juni 2023, 19:07 Uhr
Inhaltsverzeichnis
ÜBERBLICK ZUM ERSTEN HAUPTKAPITEL
Dieses erste Kapitel dient als Einführung in die gesamte Thematik, die mit den neun Büchern der Reihe $\rm LNTwww$ behandelt wird.
Im Einzelnen beschreibt dieses Kapitel:
- die Aufgaben und den prinzipiellen Aufbau eines Nachrichtenübertragungssystems,
- die wichtigsten Funktionseinheiten (Quelle, Sender, Kanal, Empfänger und Sinke) eines solchen Systems, und schließlich
- eine Klassifizierung der in einem Nachrichtensystem auftretenden Signale nach mehreren Beurteilungskriterien: deterministisch oder stochastisch, energie– oder leistungsbegrenzt, zeitkontinuierlich oder zeitdiskret, wertkontinuierlich oder wertdiskret, analog oder digital.
Am Kapitelende folgt eine kurze Zusammenfassung über das Rechnen mit komplexen Zahlen.
Nachricht - Information - Signal
Man unterscheidet grundsätzlich zwischen den Begriffen „Nachricht” und „Information”, die heutzutage allerdings oft synonym verwendet werden.
$\text{Beispiel 1:}$ Eine Email von Herrn Maier an Frau Müller ist stets eine „Nachricht”. Für Frau Müller bedeutet der Erhalt dieser Email allerdings nur dann einen Informationsgewinn, wenn sie dadurch etwas Neues erfährt. Die durch eine Nachricht übermittelte „'Information” hängt also in starkem Maße vom Kenntnisstand des Empfängers ab. In der Praxis ist die in einer Nachricht enthaltene Information eher gering, insbesondere im Anwendungsbereich der Telefonie.
Für die Übertragung und die Speicherung einer Nachricht ist stets ein energetischer bzw. materieller Träger erforderlich, der „Signal” genannt wird. Physikalisch erfolgt die Darstellung einer Nachricht also durch Signale, die von ganz unterschiedlicher Natur sein können.
Mögliche Erscheinungsformen sind:
- elektrische Signale (zum Beispiel Strom- und Spannungsverlauf),
- elektromagnetische Wellen (zum Beispiel bei der Funkübertragung),
- Zeitverlauf von Druck, Temperatur oder anderer physikalischer Größen,
- akustische Signale (zum Beispiel Ausgangssignal eines Lautsprechers),
- optische Signale (zum Beispiel Ausgangssignal eines Lasers).
$\text{Bitte beachten Sie:}$
- Die zur $\text{Nachrichtenübertragung}$ verwendeten Signale sind in der Regel Zeitfunktionen. Das bedeutet, dass (zumindest) einer der Signalparameter abhängig vom Zeitparameter $t$ ist. Solche Signalparameter sind beispielsweise bei einem Signalton die Amplitude („Lautstärke“) und die Frequenz („Tonhöhe“).
- In einem $\text{Nachrichtenspeicher}$ werden die Zeitfunktionen oft auch auf räumliche Funktionen geeigneter physikalischer Größen wie Magnetisierung (Magnetband) oder Schwärzungsgrad (Film) abgebildet.
Die Menge aller Nachrichtensignale lassen sich nach verschiedenen Kriterien katalogisieren, wie im Kapitel Klassifizierung von Signalen angegeben.
Blockschaltbild eines Nachrichtenübertragungssystems
In der folgenden Grafik ist ein Nachrichtenübertragungssystem schematisch dargestellt.
Die einzelnen Systemkomponenten haben folgende Aufgaben:
- Die Nachrichtenquelle liefert das Quellensignal $q(t)$, das über den Nachrichtenkanal zur räumlich entfernten Sinke übertragen werden soll. Die Nachrichtenquelle kann zum Beispiel ein Computer, ein Radiosender oder ein Fernsprechteilnehmer sein.
- Meist ist das Quellensignal $q(t)$ selbst für die Übertragung ungeeignet und muss erst in geeigneter Weise in das Signal $s(t)$ umgewandelt werden. Dieser Vorgang wird „Modulation” genannt und vom Sender bewerkstelligt. Deshalb wird $s(t)$ im Folgenden als Sendesignal bezeichnet.
- Bei der Übertragung über den Kanal wird dieses Signal $s(t)$ in seiner Form verändert; gleichzeitig addieren sich mehr oder weniger starke Stör– und Rauschsignale. Das Signal am Kanalausgang und gleichzeitig am Empfängereingang bezeichnen wir als das Empfangssignal $r(t)$.
- Der Empfänger muss die beim Sender vorgenommene Wandlung wieder rückgängig machen. Wurde beispielsweise das niederfrequente Quellensignal $q(t)$ in das höherfrequente Sendesignal $s(t)$ umgesetzt, so muss der Empfänger auch einen Demodulator beinhalten, der diese Umsetzung rückgängig macht.
- Der letzte Block in obigem Modell ist die Nachrichtensinke. Das Sinkensignal $v(t)$ ist wie das zu übertragende Signal $q(t)$ wieder niederfrequent. Im Idealfall, der in der Praxis allerdings (aufgrund des unvermeidbaren Rauschens) nie exakt erreicht werden kann, sollte für alle Zeiten $v(t) = q(t)$ gelten.
Nachrichtenquelle
Als Beispiele für Nachrichtenquellen bzw. für das Quellensignal $q(t)$ können genannt werden:
- Audiosignale, zum Beispiel Sprache oder Musik,
- Videosignale, zum Beispiel ein analoges Fernsehsignal oder ein MPEG-codiertes Streaming-Video,
- Datensignale, zum Beispiel der Datenstrom einer USB-Schnittstelle oder eine Email im Internet,
- Mess–Signale, zum Beispiel zur Steuerung oder zur Regelung in einem Produktionsprozess.
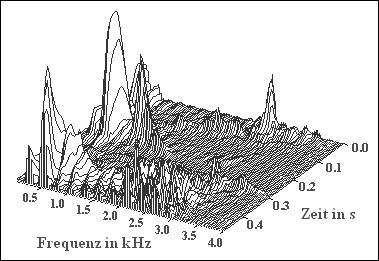
$\text{Beispiel 2:}$ Rechts sehen Sie die Frequenz–Zeitdarstellung eines Sprachsignals.
- Man erkennt zu unterschiedlichen Zeiten die verschiedenen Frequenzanteile im Kilohertz-Bereich.
- Übrigens: Es handelt sich hierbei um einen männlichen Sprecher.
Wir bedanken uns bei Markus Kaindl [1], LNT/TUM, für die Bereitstellung der Grafik.
Man unterscheidet zwischen analogen und digitalen Nachrichtenquellen. Die in diesem Buch „Signaldarstellung” dargelegten Beschreibungsformen gelten für Analogsignale und Digitalsignale gleichermaßen.
Die grundlegenden Unterschiede zwischen analogen und digitalen Signale werden
- im Kapitel Klassifizierung von Signalen behandelt, und
- durch das Lernvideo Analoge und digitale Signale an Beispielen verdeutlicht.
Aufgaben des Senders
Wesentliche Aufgabe des Senders ist es, das Quellensignal $q(t)$ derart in ein Sendesignal $s(t)$ umzuformen, dass dieses unter Einhaltung vorgegebener Leistungsmerkmale möglichst gut an den Übertragungskanal angepasst ist. Dazu enthält jeder Sender entsprechende Funktionseinheiten wie
- Wandler – zum Beispiel ein Mikrofon zur Umwandlung der physikalischen Größe „Druck” (akustische Welle) in ein elektrisches Signal,
- Signalumsetzer – beispielsweise von „analog” nach „digital” mit Hilfe der Komponenten Abtastung, Quantisierung und Binärcodierung,
- Codierer zum Entfernen von Redundanz zur Datenkomprimierung (Quellencodierung) oder zum systematischen Hinzufügen von Redundanz, die beim Empfänger zur Fehlererkennung und/oder Fehlerkorrektur genutzt werden kann (Kanalcodierung),
- Modulator zur Anpassung an den Übertragungskanal – zum Beispiel eine Frequenzumsetzung mittels Amplituden-, Phasen- oder Frequenzmodulation bzw. den entsprechenden digitalen Verfahren ASK, PSK bzw. FSK.
Je nach Anwendung bedeuten die oben angesprochenen Leistungsmerkmale, dass für die Signalübertragung ganz spezifische Eigenschaften gefordert werden.
Solche Merkmale sind beispielsweise:
- Leistungsbegrenzung – aufgrund der Diskussionen zum Thema „Elektrosmog” hochaktuell,
- Bandbreiteneffizienz – die UMTS–Versteigerung im Jahr 2000 hat gezeigt, um welche Beträge es hierbei geht,
- Distanz bzw. Reichweite – ungünstige Werte erhöhen die Infrastrukturkosten,
- Übertragungsqualität – zum Beispiel ein hoher Signal–zu–Störabstand oder eine geringe Fehlerrate.
Übertragungskanal
Bei der Realisierbarkeit bestimmter Übertragungseigenschaften spielt das Übertragungsmedium mit seinen physikalischen Eigenschaften eine wesentliche Rolle.
Beispiele für Übertragungsmedien sind:
- elektrische Leitungen, zum Beispiel Kupferdraht, Twisted Pair,
- Koaxialkabel, zum Beispiel Antennenleitung oder Kabelnetz,
- Lichtwellenleiter, zum Beispiel Multimode- und Monomodeglasfaser,
- Funkkanäle, zum Beispiel Rundfunk, Mobilfunk und Satellitenfunk.
$\text{Bitte beachten Sie:}$ Diese Übertragungsmedien sind in der Praxis nicht ideal und beeinträchtigen die Übertragung.
Das bedeutet: Das Empfangssignal $r(t)$ unterscheidet sich vom Sendesignal $s(t)$, möglicherweise aufgrund
- der Kanaldämpfung,
- von Laufzeiten auf dem Kanal,
- von Verzerrungen linearer und nichtlinearer Art.
Hinzu kommt, dass sich die Kanalübertragungseigenschaften mit der Zeit stark verändern können („Zeitvarianz”, Beispiel: Mobilfunk).
Zusätzlich sind stets die bei der Signalübertragung auftretenden Störsignale zu berücksichtigen. Hier kann man als Beispiele nennen:
- Rauschsignale – zum Beispiel Widerstands- und Halbleiterrauschen,
- Impulsstörungen – zum Beispiel Starkstromleitungen, Funkenstörungen und Entladungen,
- Nachbarkanalstörungen (Übersprechen anderer Nutzer, Interferenzen, Kreuzmodulation).
Sie finden Grundlegendes über die Modellierung des Nachrichtenkanals allgemein und des einfachen AWGN-Kanals im Lernvideo Eigenschaften des Übertragungskanals.
Empfänger – Nachrichtensinke
Als Beispiele für die Nachrichtensinke können wir nennen:
- Auge und Ohr des Menschen,
- Videorecorder und Anrufaufzeichner,
- ein Smartphone, das eine Datei aus dem Internet herunterlädt, oder
- eine Steuerungsanlage, die empfangene Mess–Signale verarbeitet.
Damit zumindest im – in der Praxis allerdings nie erreichbaren – Idealfall das Sinkensignal $v(t)$ mit dem Quellensignal $q(t)$ übereinstimmen könnte, müssen durch den Empfänger alle sendeseitig getroffenen Maßnahmen rückgängig gemacht werden.
Entsprechende Funktionseinheiten des Empfängers sind:
- Wandler – zum Beispiel ein Lautsprecher zur Umwandlung eines elektrischen in ein akustisches Signal $($Gegenstück zum Mikrofon$)$,
- Demodulation – zum Beispiel Frequenzrücksetzung des Signals in den ursprünglichen Frequenzbereich $($Gegenstück zum AM/FM/PM–Modulator$)$,
- Signalrücksetzung – zum Beispiel die Rekonstruktion des Analogsignals aus den digitalen Abtastwerten $($D/A–Wandler ⇒ Gegenstück zum A/D-Wandler$)$,
- Decodierung – zum Beispiel mit der Möglichkeit zur Fehlererkennung und Fehlerkorrektur $($Gegenstück zum Kanalcodierer$)$.
Eine weitere wichtige Aufgabe des Empfängers besteht darin, die bei der Übertragung aufgetretenen Signalverfälschungen und Störungen möglichst gut zu beseitigen.
Die Realisierung solcher Systemkomponenten für Sender und Empfänger geschieht durch verschiedene elektrische Netzwerke und Baugruppen.
Auch hier lassen sich beispielhaft einige Funktionseinheiten nennen:
- Verstärker, Filter und Entzerrer,
- Oszillatoren und nichtlineare Komponenten zur (De-)Modulation und Synchronisation,
- digitale Signalverarbeitungskomponenten und Signalprozessoren.
Signalverfälschungen
Es wurde bereits angesprochen, dass im Idealfall $v(t) = q(t)$ sein sollte. Gilt jedoch wie bei jedem realen Übertragungskanal $r(t) \neq s(t)$, so wird sich natürlich auch das Sinkensignal $v(t)$ vom Quellensignal $q(t)$ unterscheiden. Hierzu einige Beispiele:
$\text{Definition:}$ Man spricht von »Rauschen«, wenn für das Sinkensignal gilt:
- \[ v(t)=q(t)+n(t).\]
Der additive Rauschanteil $n(t)$ ist stets von stochastischer Natur und hat meist keinerlei Bezug zum Nachrichtensignal $q(t)$. Ein solcher Rauschterm ist bei jeder Übertragung unvermeidlich. Ist $n(t)$ extrem klein, so spricht man von „quasi–rauschfreier” Übertragung.
$\text{Definition:}$ Die Übertragung ist »verzerrungsfrei«, wenn das Sinkensignal wie folgt lautet:
- \[v(t)=\alpha \cdot q(t-\tau)+n(t).\]
Das Sinkensignal unterscheidet sich in diesem Falll vom Quellensignal – außer durch den Störanteil $n(t)$ – nur noch durch den $($für alle Frequenzen gleichen$)$ Dämpfungsfaktor $\alpha$ und die $($ebenfalls für alle Frequenzen gleiche$)$ Laufzeit $\tau$.
$\text{Definition:}$ Ist die Gleichung $v(t)=\alpha \cdot q(t-\tau)+n(t)$ nicht erfüllt, so liegen »Verzerrungen« vor.
Wie im Buch Lineare zeitinvariante Systeme beschrieben wird, unterscheidet man zwischen
Wir verweisen in diesem Zusammenhang auf das Lernvideo »Lineare und nichtlineare Verzerrungen«.
Hier nochmals in etwas anderen Worten:
- Der Dämpfungsfaktor $\alpha$ bewirkt nur, dass das Signal $v(t)$ etwas „leiser“ ist als $q(t)$; beide Signale haben aber die gleiche Form.
- Die Laufzeit $\tau$ führt dazu, dass das Signal $v(t)$ am Empfänger später ankommt, als $q(t)$ gesendet wurde.
Beide Effekte sind für eine unidirektionale Übertragung nicht sonderlich störend:
Man kann zum Beispiel immer noch von einer Live-Übertragung sprechen, wenn das Fernsehbild um (Bruchteille von) Sekunden verzögert ankommt.
Bei einer bidirektionalen Übertragung kann eine zu lange Laufzeit allerdings zu Problemen führen:
Bei einem Telefonat fallen sich dann die beiden Gesprächspartner gegenseitig ins Wort.
$\text{Beispiel 3:}$ Die hier benutzten Begriffe sollen nun an einem Bildsignal verdeutlicht werden.
Rechts sehen Sie als Orginalbild eine Farbschablone mit $291 × 218$ Pixeln und $24$ Bit Farbtiefe. Von den möglichen $2^{24} = 16\hspace{0.08cm} 777\hspace{0.08cm} 216$ Farben sind hier allerdings nur wenige benutzt.
- Im linken unteren Bild ist dem Signal additives Rauschen $n(t)$ überlagert, was sich als „Schnee” bemerkbar macht.
- Das rechte untere Bild zeigt den Einfluss von (nichtlinearen) Verzerrungen, die bei der gewählten Einstellung der CCD-Kamera sowohl zu einer Verfälschung der Helligkeitswerte als auch der Farbinformationen führen.
- Im markierten Feld der Grautreppe stimmt die Helligkeit in etwa mit dem Orginalbild (oben) überein.
- Dagegen erscheinen andere Felder als zu hell oder zu dunkel bzw. mit Fehlfarben belegt.
- Rauscheffekte spielen im rechten Bild keine Rolle im Gegensatz zum linken Bild.
Aufgaben zum Kapitel
Quellenverzeichnis
- ↑ Kaindl, M.: Kanalcodierung für Sprache und Daten in GSM-Systemen.
Dissertation. Lehrstuhl für Nachrichtentechnik, TU München. VDI Fortschritt-Berichte, Reihe 10, Nr. 764, 2005.