Signaldarstellung/Harmonische Schwingung: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
|||
| (60 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
| − | + | ==Definition und Eigenschaften== | |
| − | + | <br> | |
| + | [[Datei:Sig_T_2_3_S1_Version3.png|right|frame|Beispiel einer harmonischen Schwingung]] | ||
| − | Ihre Bedeutung hängt auch damit zusammen, dass die harmonische Schwingung die Lösung einer in vielen Disziplinen vorkommenden Differentialgleichung darstellt, die wie folgt lautet: | + | Besondere Bedeutung für die Nachrichtentechnik – aber auch in vielen Naturwissenschaften – haben harmonische Schwingungen. Die Grafik zeigt einen beispielhaften Signalverlauf. |
| + | |||
| + | Ihre Bedeutung hängt auch damit zusammen, dass die harmonische Schwingung die Lösung einer in vielen Disziplinen vorkommenden Differentialgleichung darstellt, die wie folgt lautet: | ||
| − | $ x(t) + k \cdot\ddot{x} (t) =0.$ | + | :$$ x(t) + k \cdot\ddot{x} (t) = 0.$$ |
| − | Hierbei kennzeichnen die beiden Punkte die zweite Ableitung der Funktion $x(t)$ nach der Zeit. | + | Hierbei kennzeichnen die beiden Punkte die zweite Ableitung der Funktion $x(t)$ nach der Zeit. |
| − | + | <br clear=all> | |
| − | |||
| − | $ | + | {{BlaueBox|TEXT= |
| + | $\text{Definition:}$ | ||
| + | Eine jede $\text{harmonische Schwingung}$ kann man in allgemeinster Form wie folgt darstellen: | ||
| − | + | :$$x(t)= C \cdot \cos(2\pi f_0 t - \varphi).$$ | |
Hierbei sind folgende Signalparameter verwendet: | Hierbei sind folgende Signalparameter verwendet: | ||
| − | *die | + | *die $\text{Amplitude}$ $C$ – gleichzeitig der Maximalwert des Signals, |
| − | *die | + | *die $\text{Signalfrequenz}$ $f_{0}$ ⇒ der Kehrwert der Periodendauer $T_{0}$, und |
| − | *der | + | *der $\text{Nullphasenwinkel}$ (oder kurz die Phase) $\varphi$ der Schwingung.}} |
| − | + | ||
| − | Zur Unterscheidung der beiden Varianten benutzen wir in | + | Das Lernvideo [[Harmonische_Schwingungen_(Lernvideo)|Harmonische Schwingungen]] verdeutlicht die Eigenschaften harmonischer Schwingungen anhand von Tonleitern. |
| − | Die Angaben $\ | + | |
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Anmerkung zur Nomenklatur:}$ | ||
| + | *In diesem Tutorial geht – wie auch in anderer Literatur üblich – bei der Beschreibung von harmonischen Schwingungen, Fourierreihe und Fourierintegral die Phase mit negativem Vorzeichen in die Gleichungen ein, während in Zusammenhang mit allen Modulationsverfahren die Phase stets mit einem Pluszeichen angesetzt wird. | ||
| + | *Zur Unterscheidung der beiden Varianten benutzen wir in $\rm LNTwww$ $\varphi$ und $\phi$. Beide Symbole kennzeichnen das kleine griechische „phi”, wobei die Schreibweise $\varphi$ vorwiegend im deutschen und $\phi$ im anglo–amerikanischen Sprachraum angewandt wird. | ||
| + | *Die Angaben $\varphi = 90^{\circ}$ und $\phi = -90^{\circ}$ sind somit äquivalent und stehen beide für die Sinusfunktion: | ||
| + | :$$\cos(2 \pi f_0 t - 90^{\circ}) = \cos(2 \pi f_0 t - \varphi) = \cos(2 \pi f_0 t + \phi) = \sin(2 \pi f_0 t ).$$}} | ||
| + | |||
| + | |||
| + | ==Zeitsignaldarstellung== | ||
| + | <br> | ||
| + | [[Datei:P_ID129__Sig_T_2_3_S2a.png|right|frame|Signalparameter einer harmonischen Schwingung]] | ||
| + | Die Amplitude $C$ kann aus nebenstehender Grafik direkt abgelesen werden. Die Signalfrequenz $f_0$ ist gleich dem Kehrwert der Periodendauer $T_0$. Schreibt man die obige Gleichung in der Form | ||
| + | |||
| + | :$$x(t) = C \cdot \cos(2\pi f_0 t - \varphi) = C \cdot \cos \big(2\pi f_0 (t - \tau) \big), $$ | ||
| − | $ | + | so wird klar, dass der Nullphasenwinkel $\varphi$ und die Verschiebung $\tau$ gegenüber einem cosinusförmigen Signal wie folgt zusammenhängen: |
| − | + | :$$\varphi = \frac{\tau}{T_0} \cdot 2{\pi}. $$ | |
| − | |||
| − | + | *Bei einem $\text{Cosinussignal}$ sind die Kenngrößen $\tau$ und $\varphi$ jeweils Null. | |
| − | + | *Demgegenüber ist ein $\text{Sinussignal}$ um $\tau = T_0/4$ verschoben und entsprechend gilt für den Nullphasenwinkel $\varphi = \pi/2$ (im Bogenmaß) bzw. $90^{\circ}$. | |
| − | |||
| − | |||
| − | |||
| − | $\varphi | + | Es ist also festzustellen, dass – wie für die obige Skizze vorausgesetzt – bei einem positiven Wert von $\tau$ bzw. $\varphi$ das $($bezüglich $t = 0)$ nächstgelegene Signalmaximum später kommt als beim Cosinussignal und bei negativen Werten früher. Liegt am Systemeingang ein Cosinussignal an und ist das Ausgangssignal demgegenüber um einen Wert $\tau$ verzögert, so bezeichnet man $\tau$ auch als die $\text{Laufzeit}$ des Systems. |
| − | + | Da eine harmonische Schwingung durch lediglich drei Signalparameter eindeutig festliegt, kann der gesamte Zeitverlauf von $-\infty$ bis $+\infty$ aus nur drei Signalwerten $x_1=x(t_1)$, $x_2=x(t_2)$, $x_3=x(t_3)$ analytisch beschrieben werden, wenn die Zeiten $t_1$, $t_2$ und $t_3$ geeignet festgelegt wurden. | |
| − | |||
| − | Da eine harmonische Schwingung durch lediglich drei Signalparameter eindeutig festliegt, kann der gesamte Zeitverlauf von $-\infty$ bis $+\ | ||
| − | {{Beispiel} | + | [[Datei:P_ID2717__Sig_T_2_3_S2b_neu.png|right|frame|Harmonische Schwingung, <br>festgelegt durch nur drei Abtastwerte]] |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ | ||
Aus den drei Abtastwerten, | Aus den drei Abtastwerten, | ||
| − | + | :$$x_1 = x(t_1 = 3.808 \;{\rm ms}) = +1.609,$$ | |
| − | + | :$$x_2 = x(t_2 = 16.696 \;{\rm ms})=\hspace{0.05 cm} -0.469,$$ | |
| − | + | :$$x_3 = x(t_3 = 33.84 \;{\rm ms}) = +1.227$$ | |
| + | |||
erhält man folgendes Gleichungssystem: | erhält man folgendes Gleichungssystem: | ||
| − | $C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_1 - \varphi) | + | :$$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_1 - \varphi) = +1.609\hspace{0.05 cm},$$ |
| − | C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_2 - \varphi) | + | :$$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_2 - \varphi) = \hspace{0.05 cm} -0.469\hspace{0.05 cm},$$ |
| − | C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_3 - \varphi) | + | :$$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_3 - \varphi) = +1.227\hspace{0.05 cm}.$$ |
Nach Lösen dieses nichtlinearen Gleichungssystem ergeben sich folgende Signalparameter: | Nach Lösen dieses nichtlinearen Gleichungssystem ergeben sich folgende Signalparameter: | ||
| − | *Signalamplitude $C | + | *Signalamplitude $C = 2$, |
| − | *Periodendauer $T_0 | + | *Periodendauer $T_0 = 8 \;{\rm ms}$ ⇒ Signalfrequenz $f_0 = 125 \;{\rm Hz}$, |
| − | *Verschiebung gegenüber einem Cosinus $\tau | + | *Verschiebung gegenüber einem Cosinus $\tau = 3 \;{\rm ms}$ ⇒ Nullphasenwinkel $\varphi = 3\pi /4 = 135^\circ$. |
| − | + | ||
| − | + | ||
| + | Legt man alle Abtastzeitpunkte $t_1$, $t_2$, $t_3$ allerdings in Maxima, Minima und/oder Nullstellen, so gibt es für das nichtlineare Gleichungssystem keine eindeutige Lösung.}} | ||
| − | + | ==Darstellung mit Cosinus- und Sinusanteil== | |
| + | <br> | ||
Eine weitere Darstellungsform der harmonischen Schwingung lautet wie folgt: | Eine weitere Darstellungsform der harmonischen Schwingung lautet wie folgt: | ||
| − | $x(t)=A\cdot\cos(2\pi f_0 t)+ B\cdot\sin(2\pi f_0 t).$ | + | :$$x(t)=A\cdot\cos(2\pi f_0 t)+ B\cdot\sin(2\pi f_0 t).$$ |
| − | Die Bezeichnungen $A$ und $B$ für die Amplituden von | + | *Die Bezeichnungen $A$ und $B$ für die Amplituden von Cosinus– und Sinusanteil sind so gewählt, dass sie mit der Nomenklatur des folgenden Kapitels [[Signaldarstellung/Fourierreihe| Fourierreihe]] übereinstimmen. |
| − | Durch Anwendung trigonometrischer Umformungen erhalten wir aus der Darstellung auf der letzten Seite: | + | |
| + | *Durch Anwendung trigonometrischer Umformungen erhalten wir aus der Darstellung auf der letzten Seite: | ||
| − | $x(t)=C\cdot \cos(2\pi f_0 t-\varphi)=C\cdot\cos(\varphi)\cdot\cos(2\pi f_0 t)+C\cdot\sin(\varphi)\cdot\sin(2\pi f_0 t).$ | + | :$$x(t)=C\cdot \cos(2\pi f_0 t-\varphi)=C\cdot\cos(\varphi)\cdot\cos(2\pi f_0 t)+C\cdot\sin(\varphi)\cdot\sin(2\pi f_0 t).$$ |
| − | Daraus folgt durch Koeffizientenvergleich direkt: | + | *Daraus folgt durch Koeffizientenvergleich direkt: |
| − | $A=C\cdot\cos(\varphi),$ | + | :$$A=C\cdot\cos(\varphi),\hspace{0.5cm}B=C\cdot\sin(\varphi).$$ |
| − | $B | + | *Der Betrag und der Nullphasenwinkel der harmonischen Schwingung können aus den Parametern $A$ und $B$ ebenfalls nach einfachen trigonometrischen Überlegungen berechnet werden: |
| − | + | :$$C=\sqrt{A^2+B^2}, \hspace{0.5 cm}\varphi = \arctan\left({-B}/{A}\right).$$ | |
| − | + | ||
| − | $C=\sqrt{A^2+B^2}, \hspace{0. | + | {{BlaueBox|TEXT= |
| + | $\text{Bitte beachten Sie:}$ | ||
| + | |||
| + | Das Minuszeichen bei der Berechnung des Phasenwinkels $\varphi$ hängt damit zusammen, dass $\varphi$ in das Argument der Cosinusfunktion mit negativem Vorzeichen eingeht. | ||
| + | |||
| + | Würde man statt „$\cos(2\pi f_0 t - \varphi)$” die Schreibweise „$\cos(2\pi f_0 t + \phi)$” verwenden, so wäre $\phi= \arctan(B/A)$. Hier noch folgender Hinweis: | ||
| + | |||
| + | *Bei Fourierreihe und Fourierintegral ist in der Literatur die $\varphi$–Darstellung üblich. | ||
| + | *Zur Beschreibung der Modulationsverfahren verwendet man dagegen fast immer die $\phi$–Darstellungsform.}} | ||
| + | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Beispiel 2:}$ | ||
| + | Die in der linken Grafik als Zeitverlauf dargestellte Schwingung ist gekennzeichnet durch die Parameter | ||
| + | [[Datei:Sig_T_2_3_S3_version2.png|right|frame|Harmonische Schwingung, dargestellt in der komplexen Ebene]] | ||
| + | :*$C=0,$ | ||
| + | :*$f_0 = 125 \;{\rm Hz}$, | ||
| + | :*$\varphi = +135^{\circ}$ ⇒ $\phi = -135^{\circ}$ . | ||
| − | |||
| − | |||
| − | + | Die Schwingung wird durch jede der beiden Gleichungen vollständig beschrieben: | |
| − | Die | ||
| − | $x(t)\hspace{-0. | + | :$$x(t) \hspace{-0.05cm}=\hspace{-0.05cm} 2\cdot \cos(2\pi f_0 t-135^{\circ})\hspace{0.05cm},$$ |
| − | x(t)\hspace{-0. | + | :$$x(t) \hspace{-0.05cm}=\hspace{-0.05cm} -\sqrt{2}\cdot \cos(2\pi f_0 t) \hspace{-0.05cm}+\hspace{-0.05cm}\sqrt{2}\cdot \sin(2\pi f_0 t)\hspace{0.05cm}.$$ |
Die rechte Skizze verdeutlicht die trigonometrische Umformung: | Die rechte Skizze verdeutlicht die trigonometrische Umformung: | ||
| − | $A | + | :$$A = 2\cdot \cos(-135^{\circ}) = -\sqrt{2}\hspace{0.05cm},$$ |
| − | B | + | :$$B = 2\cdot \sin(-135^{\circ}) = +\sqrt{2}\hspace{0.05cm}.$$}} |
| + | |||
| + | |||
| + | ==Spektraldarstellung eines Cosinussignals== | ||
| + | <br> | ||
| + | Zur Herleitung der Spektralfunktion beschränken wir uns zunächst auf ein Cosinussignal, das mit der komplexen Exponentialfunktion und dem [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Darstellung_nach_Betrag_und_Phase|Satz von Euler]] auch in folgender Weise geschrieben werden kann: | ||
| + | |||
| + | :$$x(t)=A \cdot \cos(2\pi f_0 t)={A}/{2}\cdot \big [{\rm e}^{\rm -j2 \pi \it f_{\rm 0} t} + {\rm e}^{\rm j2\pi \it f_{\rm 0} t} \big ].$$ | ||
| − | + | Bereits aus dieser Darstellung ist ersichtlich, dass das Cosinussignal – spektral gesehen – nur eine einzige (physikalische) Frequenz beinhaltet, nämlich die Frequenz $f_0$. | |
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Beweis:}$ Zur mathematischen Herleitung der Spektralfunktion benutzen wir folgende Beziehungen: | ||
| + | *den auf der Seite [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals#Diracfunktion_im_Frequenzbereich|Diracfunktion im Frequenzbereich]] hergeleiteten Funktionalzusammenhang: | ||
| + | :$$x(t)=A \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)=A \cdot \rm \delta (\it f).$$ | ||
| − | + | *den [[Signaldarstellung/Gesetzm%C3%A4%C3%9Figkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatz (für den Frequenzbereich)]] im Vorgriff auf ein späteres Kapitel: | |
| + | :$$x(t) \cdot {\rm e}^{\rm j2\pi\it f_{\rm 0} t}\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f-f_0). $$ | ||
| − | + | Daraus ergibt sich die folgende Fourierkorrespondenz: | |
| − | $x(t)=A \cdot \cos(2\pi | + | :$$x(t)=A\cdot \cos(2\pi f_0t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)={A}/{\rm 2}\cdot {\rm \delta} (f+f_{\rm 0})+{A}/{\rm 2}\cdot {\rm \delta}(\ f-f_{\rm 0}).$$ |
| − | + | Das bedeutet: | |
| − | + | *Die Spektralfunktion $X(f)$ eines Cosinussignals mit der Frequenz $f_0$ setzt sich aus zwei Diracfunktionen bei $\pm f_0$ zusammen. | |
| − | * | + | * Die Impulsgewichte sind jeweils gleich der halben Signalamplitude.}} |
| − | |||
| − | |||
| − | |||
| − | + | [[Datei:P_ID1365__Sig_T_2_3_S4_neu.png|right|frame|Spektrum eines Cosinussignals]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 3:}$ | ||
| + | Die Grafik zeigt das Spektrum einer Cosinusschwingung | ||
| + | |||
| + | *mit der Amplitude $A = 4 \;{\rm V}$ und | ||
| + | *der Frequenz $f_0 = 5 \;{\rm kHz}$ ⇒ $T_0 = 200 \;{\rm µ s}$. | ||
| + | |||
| + | |||
| + | Dann gilt folgender Zusammenhang mit obiger Gleichung: | ||
| + | *Die Diracfunktion bei $-f_0$ gehört zum ersten Term $($ableitbar aus der Bedingung $f + f_0 = 0)$. | ||
| + | *Die Diracfunktion bei $+f_0$ gehört zum zweiten Term $($ableitbar aus der Bedingung $f - f_0 = 0)$. | ||
| + | *Die Impulsgewichte sind jeweils $A/2 = 2 \;{\rm V}$.}} | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Bitte beachten Sie:}$ | ||
| − | + | Die Spektralfunktion einer jeden reellen Zeitfunktion mit Ausnahme des Gleichsignals weist sowohl Anteile bei positiven als auch bei negativen Frequenzen auf. | |
| − | + | *Diese Tatsache, die Studienanfängern oft Probleme bereitet, ergibt sich ganz formal aus dem [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Darstellung_nach_Betrag_und_Phase|Satz von Euler]] . | |
| − | + | *Durch Erweiterung des Frequenzwertebereichs von $f \ge 0$ auf die Menge der reellen Zahlen kommt man von der physikalischen zur „mathematischen„ Frequenz. | |
| + | *Allerdings ist für eine negative Frequenz die vorne angegebene [[Signaldarstellung/Harmonische_Schwingung#Definition_und_Eigenschaften|Definition]] nicht mehr anwendbar: <br> Man kann „–5 kHz” nicht als „minus 5000 Schwingungen pro Sekunde” interpretieren. | ||
| − | |||
| − | |||
| − | |||
| − | + | Im Verlauf dieses Kurses werden Sie feststellen, dass durch die Verkomplizierung dieses einfachen Sachverhaltes später kompliziertere Sachverhalte sehr elegant und einfach beschrieben werden können.}} | |
| − | Im Verlauf dieses Kurses werden Sie feststellen, dass durch die Verkomplizierung | ||
| − | + | ==Allgemeine Spektraldarstellung== | |
| + | <br> | ||
| + | Für ein sinusförmiges Signal gilt mit dem Satz von [https://de.wikipedia.org/wiki/Leonhard_Euler Euler] in ähnlicher Weise: | ||
| − | + | :$$x(t)=B\cdot \sin(2 \pi f_0 t)= \frac{\it B}{2 \rm j} \cdot \big [{\rm e}^{+{\rm j} 2 \pi \it f_{\rm 0} t}-{\rm e}^{-\rm j2 \pi \it f_{\rm 0} t}\big ]=\rm j\cdot {\it B}/{2} \cdot \big [{\rm e}^{-j2 \pi \it f_{\rm 0} t}-{\rm e}^{+\rm j2 \pi \it f_{\rm 0} t} \big ] .$$ | |
| − | + | Daraus folgt für die Spektralfunktion, die jetzt rein imaginär ist: | |
| − | + | :$$x(t)=B\cdot \sin(2\pi f_0 t)\;\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\; \ X(f)={\rm j} \cdot \big [ {B}/{2} \cdot \delta (f+f_0)- {B}/{2} \cdot \delta (f-f_0) \big ].$$ | |
| + | |||
| + | [[Datei: P_ID2719__Sig_T_2_3_S5.png |right|frame|Spektrum eines Sinussignals]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 4:}$ | ||
| + | Das Bild zeigt die rein imaginäre Spektralfunktion einer Sinusschwingung $x(t)$ mit | ||
| + | *Amplitude $B = 3 \;{\rm V},$ | ||
| + | *Frequenz $f_0 = 5\;{\rm kHz},$ | ||
| + | *Phase $\varphi=90^{\circ}$ ⇒ $\phi = -90^{\circ}$. | ||
| + | <br>$\text{Bitte beachten Sie}$: | ||
| − | $ | + | *Bei der positiven Frequenz $(f = +f_0)$ ist der Imaginärteil negativ. |
| + | |||
| + | *Bei der negativen Frequenz $(f = -f_0)$ ergibt sich ein positiver Imaginärteil.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
Bei Überlagerung von Cosinus– und Sinusanteil entsprechend der Beziehung | Bei Überlagerung von Cosinus– und Sinusanteil entsprechend der Beziehung | ||
| − | $x(t)=A \cdot \cos(2\pi f_0 t) +B \cdot \sin(2 \pi f_0 t)$ | + | :$$x(t)=A \cdot \cos(2\pi f_0 t) +B \cdot \sin(2 \pi f_0 t)$$ |
überlagern sich auch die einzelnen Spektralfunktionen und man erhält: | überlagern sich auch die einzelnen Spektralfunktionen und man erhält: | ||
| − | $X(f)=\frac{A+{\rm j} \cdot B}{2}\ | + | :$$X(f)=\frac{A+{\rm j} \cdot B}{2}\cdot {\rm \delta} (f+f_0)+\frac{A-{\rm j} \cdot B}{2} \cdot \delta (f-f_0).$$ |
| − | Mit dem Betrag $C$ und der Phase $\ | + | Mit dem Betrag $C$ und der Phase $\varphi$ lautet diese Fourierkorrespondenz: |
| − | $x(t)=C\cdot \cos(2\pi f_0 t-\varphi) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f)= | + | :$$x(t)=C\cdot \cos(2\pi f_0 t-\varphi)\ \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ X(f)={C}/{2}\cdot {\rm e}^{{\rm j} \varphi} \cdot \delta(f+f_0) + {C}/{2} \cdot {\rm e}^{\rm{-j} \varphi} \cdot \delta (f-f_0).$$ |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Man erkennt:}$ Die Spektralfunktion $X(f)$ | ||
| + | *ist nicht nur für positive und negative Frequenzen definiert, | ||
| + | *sondern im Allgemeinen auch noch komplexwertig.}} | ||
| + | |||
| + | |||
| + | [[Datei:Sig_T_2_3_S6_version2.png|right|frame|Spektrum der Schwingung mit $\varphi=30^{\circ}$]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 5:}$ | ||
| + | Mit den Parametern $C = 5 \;{\rm V}$, $f_0 = 5\;{\rm kHz}$ und $\varphi=30^{\circ}$ $($im Bogenmaß $\pi/6)$ ergibt sich wegen | ||
| + | |||
| + | :$$2.5 · \cos(30^{\circ}) = 2.165, \hspace{0.3cm} 2.5 · \sin(30^{\circ}) = 1.25$$ | ||
| + | der Real- bzw. der Imaginärteil von $X(f)$ gemäß der Grafik: | ||
| − | + | :$${\rm Re}\big[X(f)\big]=2.165\,{\rm V} \cdot \delta(f+f_0) + 2.165\,{\rm V} \cdot \delta (f-f_0).$$ | |
| − | |||
| − | + | :$${\rm Im}\big[X(f)\big]=1.25\,{\rm V} \cdot \delta(f+f_0) -1.25\,{\rm V} \cdot \delta (f-f_0).$$}} | |
| − | |||
| − | |||
| + | Das Lernvideo | ||
| + | [[Harmonische_Schwingungen_(Lernvideo)|Harmonische Schwingungen]] verdeutlicht die Eigenschaften harmonischer Schwingungen anhand der so genannten Tonleiter. | ||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:2.3 cos- und sin-Anteil|Aufgabe 2.3: Cosinus- und Sinusanteil]] | ||
| + | [[Aufgaben:Aufgabe 2.3Z:_ Schwingungsparameter|Aufgabe 2.3: Schwingungsparameter]] | ||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 9. Juni 2023, 16:43 Uhr
Inhaltsverzeichnis
Definition und Eigenschaften
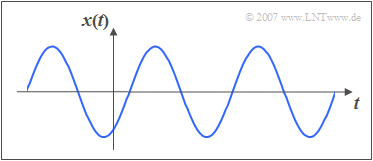
Besondere Bedeutung für die Nachrichtentechnik – aber auch in vielen Naturwissenschaften – haben harmonische Schwingungen. Die Grafik zeigt einen beispielhaften Signalverlauf.
Ihre Bedeutung hängt auch damit zusammen, dass die harmonische Schwingung die Lösung einer in vielen Disziplinen vorkommenden Differentialgleichung darstellt, die wie folgt lautet:
- $$ x(t) + k \cdot\ddot{x} (t) = 0.$$
Hierbei kennzeichnen die beiden Punkte die zweite Ableitung der Funktion $x(t)$ nach der Zeit.
$\text{Definition:}$ Eine jede $\text{harmonische Schwingung}$ kann man in allgemeinster Form wie folgt darstellen:
- $$x(t)= C \cdot \cos(2\pi f_0 t - \varphi).$$
Hierbei sind folgende Signalparameter verwendet:
- die $\text{Amplitude}$ $C$ – gleichzeitig der Maximalwert des Signals,
- die $\text{Signalfrequenz}$ $f_{0}$ ⇒ der Kehrwert der Periodendauer $T_{0}$, und
- der $\text{Nullphasenwinkel}$ (oder kurz die Phase) $\varphi$ der Schwingung.
Das Lernvideo Harmonische Schwingungen verdeutlicht die Eigenschaften harmonischer Schwingungen anhand von Tonleitern.
$\text{Anmerkung zur Nomenklatur:}$
- In diesem Tutorial geht – wie auch in anderer Literatur üblich – bei der Beschreibung von harmonischen Schwingungen, Fourierreihe und Fourierintegral die Phase mit negativem Vorzeichen in die Gleichungen ein, während in Zusammenhang mit allen Modulationsverfahren die Phase stets mit einem Pluszeichen angesetzt wird.
- Zur Unterscheidung der beiden Varianten benutzen wir in $\rm LNTwww$ $\varphi$ und $\phi$. Beide Symbole kennzeichnen das kleine griechische „phi”, wobei die Schreibweise $\varphi$ vorwiegend im deutschen und $\phi$ im anglo–amerikanischen Sprachraum angewandt wird.
- Die Angaben $\varphi = 90^{\circ}$ und $\phi = -90^{\circ}$ sind somit äquivalent und stehen beide für die Sinusfunktion:
- $$\cos(2 \pi f_0 t - 90^{\circ}) = \cos(2 \pi f_0 t - \varphi) = \cos(2 \pi f_0 t + \phi) = \sin(2 \pi f_0 t ).$$
Zeitsignaldarstellung
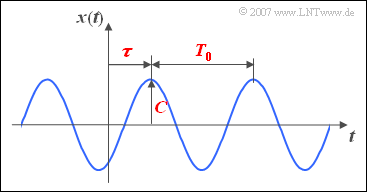
Die Amplitude $C$ kann aus nebenstehender Grafik direkt abgelesen werden. Die Signalfrequenz $f_0$ ist gleich dem Kehrwert der Periodendauer $T_0$. Schreibt man die obige Gleichung in der Form
- $$x(t) = C \cdot \cos(2\pi f_0 t - \varphi) = C \cdot \cos \big(2\pi f_0 (t - \tau) \big), $$
so wird klar, dass der Nullphasenwinkel $\varphi$ und die Verschiebung $\tau$ gegenüber einem cosinusförmigen Signal wie folgt zusammenhängen:
- $$\varphi = \frac{\tau}{T_0} \cdot 2{\pi}. $$
- Bei einem $\text{Cosinussignal}$ sind die Kenngrößen $\tau$ und $\varphi$ jeweils Null.
- Demgegenüber ist ein $\text{Sinussignal}$ um $\tau = T_0/4$ verschoben und entsprechend gilt für den Nullphasenwinkel $\varphi = \pi/2$ (im Bogenmaß) bzw. $90^{\circ}$.
Es ist also festzustellen, dass – wie für die obige Skizze vorausgesetzt – bei einem positiven Wert von $\tau$ bzw. $\varphi$ das $($bezüglich $t = 0)$ nächstgelegene Signalmaximum später kommt als beim Cosinussignal und bei negativen Werten früher. Liegt am Systemeingang ein Cosinussignal an und ist das Ausgangssignal demgegenüber um einen Wert $\tau$ verzögert, so bezeichnet man $\tau$ auch als die $\text{Laufzeit}$ des Systems.
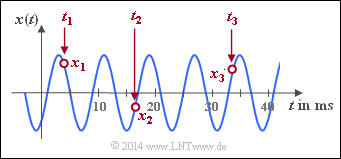
Da eine harmonische Schwingung durch lediglich drei Signalparameter eindeutig festliegt, kann der gesamte Zeitverlauf von $-\infty$ bis $+\infty$ aus nur drei Signalwerten $x_1=x(t_1)$, $x_2=x(t_2)$, $x_3=x(t_3)$ analytisch beschrieben werden, wenn die Zeiten $t_1$, $t_2$ und $t_3$ geeignet festgelegt wurden.
$\text{Beispiel 1:}$ Aus den drei Abtastwerten,
- $$x_1 = x(t_1 = 3.808 \;{\rm ms}) = +1.609,$$
- $$x_2 = x(t_2 = 16.696 \;{\rm ms})=\hspace{0.05 cm} -0.469,$$
- $$x_3 = x(t_3 = 33.84 \;{\rm ms}) = +1.227$$
erhält man folgendes Gleichungssystem:
- $$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_1 - \varphi) = +1.609\hspace{0.05 cm},$$
- $$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_2 - \varphi) = \hspace{0.05 cm} -0.469\hspace{0.05 cm},$$
- $$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_3 - \varphi) = +1.227\hspace{0.05 cm}.$$
Nach Lösen dieses nichtlinearen Gleichungssystem ergeben sich folgende Signalparameter:
- Signalamplitude $C = 2$,
- Periodendauer $T_0 = 8 \;{\rm ms}$ ⇒ Signalfrequenz $f_0 = 125 \;{\rm Hz}$,
- Verschiebung gegenüber einem Cosinus $\tau = 3 \;{\rm ms}$ ⇒ Nullphasenwinkel $\varphi = 3\pi /4 = 135^\circ$.
Legt man alle Abtastzeitpunkte $t_1$, $t_2$, $t_3$ allerdings in Maxima, Minima und/oder Nullstellen, so gibt es für das nichtlineare Gleichungssystem keine eindeutige Lösung.
Darstellung mit Cosinus- und Sinusanteil
Eine weitere Darstellungsform der harmonischen Schwingung lautet wie folgt:
- $$x(t)=A\cdot\cos(2\pi f_0 t)+ B\cdot\sin(2\pi f_0 t).$$
- Die Bezeichnungen $A$ und $B$ für die Amplituden von Cosinus– und Sinusanteil sind so gewählt, dass sie mit der Nomenklatur des folgenden Kapitels Fourierreihe übereinstimmen.
- Durch Anwendung trigonometrischer Umformungen erhalten wir aus der Darstellung auf der letzten Seite:
- $$x(t)=C\cdot \cos(2\pi f_0 t-\varphi)=C\cdot\cos(\varphi)\cdot\cos(2\pi f_0 t)+C\cdot\sin(\varphi)\cdot\sin(2\pi f_0 t).$$
- Daraus folgt durch Koeffizientenvergleich direkt:
- $$A=C\cdot\cos(\varphi),\hspace{0.5cm}B=C\cdot\sin(\varphi).$$
- Der Betrag und der Nullphasenwinkel der harmonischen Schwingung können aus den Parametern $A$ und $B$ ebenfalls nach einfachen trigonometrischen Überlegungen berechnet werden:
- $$C=\sqrt{A^2+B^2}, \hspace{0.5 cm}\varphi = \arctan\left({-B}/{A}\right).$$
$\text{Bitte beachten Sie:}$
Das Minuszeichen bei der Berechnung des Phasenwinkels $\varphi$ hängt damit zusammen, dass $\varphi$ in das Argument der Cosinusfunktion mit negativem Vorzeichen eingeht.
Würde man statt „$\cos(2\pi f_0 t - \varphi)$” die Schreibweise „$\cos(2\pi f_0 t + \phi)$” verwenden, so wäre $\phi= \arctan(B/A)$. Hier noch folgender Hinweis:
- Bei Fourierreihe und Fourierintegral ist in der Literatur die $\varphi$–Darstellung üblich.
- Zur Beschreibung der Modulationsverfahren verwendet man dagegen fast immer die $\phi$–Darstellungsform.
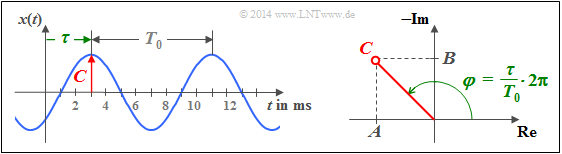
$\text{Beispiel 2:}$ Die in der linken Grafik als Zeitverlauf dargestellte Schwingung ist gekennzeichnet durch die Parameter
- $C=0,$
- $f_0 = 125 \;{\rm Hz}$,
- $\varphi = +135^{\circ}$ ⇒ $\phi = -135^{\circ}$ .
Die Schwingung wird durch jede der beiden Gleichungen vollständig beschrieben:
- $$x(t) \hspace{-0.05cm}=\hspace{-0.05cm} 2\cdot \cos(2\pi f_0 t-135^{\circ})\hspace{0.05cm},$$
- $$x(t) \hspace{-0.05cm}=\hspace{-0.05cm} -\sqrt{2}\cdot \cos(2\pi f_0 t) \hspace{-0.05cm}+\hspace{-0.05cm}\sqrt{2}\cdot \sin(2\pi f_0 t)\hspace{0.05cm}.$$
Die rechte Skizze verdeutlicht die trigonometrische Umformung:
- $$A = 2\cdot \cos(-135^{\circ}) = -\sqrt{2}\hspace{0.05cm},$$
- $$B = 2\cdot \sin(-135^{\circ}) = +\sqrt{2}\hspace{0.05cm}.$$
Spektraldarstellung eines Cosinussignals
Zur Herleitung der Spektralfunktion beschränken wir uns zunächst auf ein Cosinussignal, das mit der komplexen Exponentialfunktion und dem Satz von Euler auch in folgender Weise geschrieben werden kann:
- $$x(t)=A \cdot \cos(2\pi f_0 t)={A}/{2}\cdot \big [{\rm e}^{\rm -j2 \pi \it f_{\rm 0} t} + {\rm e}^{\rm j2\pi \it f_{\rm 0} t} \big ].$$
Bereits aus dieser Darstellung ist ersichtlich, dass das Cosinussignal – spektral gesehen – nur eine einzige (physikalische) Frequenz beinhaltet, nämlich die Frequenz $f_0$.
$\text{Beweis:}$ Zur mathematischen Herleitung der Spektralfunktion benutzen wir folgende Beziehungen:
- den auf der Seite Diracfunktion im Frequenzbereich hergeleiteten Funktionalzusammenhang:
- $$x(t)=A \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)=A \cdot \rm \delta (\it f).$$
- den Verschiebungssatz (für den Frequenzbereich) im Vorgriff auf ein späteres Kapitel:
- $$x(t) \cdot {\rm e}^{\rm j2\pi\it f_{\rm 0} t}\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f-f_0). $$
Daraus ergibt sich die folgende Fourierkorrespondenz:
- $$x(t)=A\cdot \cos(2\pi f_0t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)={A}/{\rm 2}\cdot {\rm \delta} (f+f_{\rm 0})+{A}/{\rm 2}\cdot {\rm \delta}(\ f-f_{\rm 0}).$$
Das bedeutet:
- Die Spektralfunktion $X(f)$ eines Cosinussignals mit der Frequenz $f_0$ setzt sich aus zwei Diracfunktionen bei $\pm f_0$ zusammen.
- Die Impulsgewichte sind jeweils gleich der halben Signalamplitude.
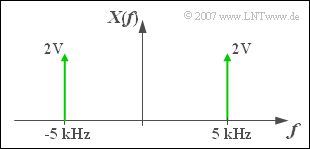
$\text{Beispiel 3:}$ Die Grafik zeigt das Spektrum einer Cosinusschwingung
- mit der Amplitude $A = 4 \;{\rm V}$ und
- der Frequenz $f_0 = 5 \;{\rm kHz}$ ⇒ $T_0 = 200 \;{\rm µ s}$.
Dann gilt folgender Zusammenhang mit obiger Gleichung:
- Die Diracfunktion bei $-f_0$ gehört zum ersten Term $($ableitbar aus der Bedingung $f + f_0 = 0)$.
- Die Diracfunktion bei $+f_0$ gehört zum zweiten Term $($ableitbar aus der Bedingung $f - f_0 = 0)$.
- Die Impulsgewichte sind jeweils $A/2 = 2 \;{\rm V}$.
$\text{Bitte beachten Sie:}$
Die Spektralfunktion einer jeden reellen Zeitfunktion mit Ausnahme des Gleichsignals weist sowohl Anteile bei positiven als auch bei negativen Frequenzen auf.
- Diese Tatsache, die Studienanfängern oft Probleme bereitet, ergibt sich ganz formal aus dem Satz von Euler .
- Durch Erweiterung des Frequenzwertebereichs von $f \ge 0$ auf die Menge der reellen Zahlen kommt man von der physikalischen zur „mathematischen„ Frequenz.
- Allerdings ist für eine negative Frequenz die vorne angegebene Definition nicht mehr anwendbar:
Man kann „–5 kHz” nicht als „minus 5000 Schwingungen pro Sekunde” interpretieren.
Im Verlauf dieses Kurses werden Sie feststellen, dass durch die Verkomplizierung dieses einfachen Sachverhaltes später kompliziertere Sachverhalte sehr elegant und einfach beschrieben werden können.
Allgemeine Spektraldarstellung
Für ein sinusförmiges Signal gilt mit dem Satz von Euler in ähnlicher Weise:
- $$x(t)=B\cdot \sin(2 \pi f_0 t)= \frac{\it B}{2 \rm j} \cdot \big [{\rm e}^{+{\rm j} 2 \pi \it f_{\rm 0} t}-{\rm e}^{-\rm j2 \pi \it f_{\rm 0} t}\big ]=\rm j\cdot {\it B}/{2} \cdot \big [{\rm e}^{-j2 \pi \it f_{\rm 0} t}-{\rm e}^{+\rm j2 \pi \it f_{\rm 0} t} \big ] .$$
Daraus folgt für die Spektralfunktion, die jetzt rein imaginär ist:
- $$x(t)=B\cdot \sin(2\pi f_0 t)\;\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\; \ X(f)={\rm j} \cdot \big [ {B}/{2} \cdot \delta (f+f_0)- {B}/{2} \cdot \delta (f-f_0) \big ].$$
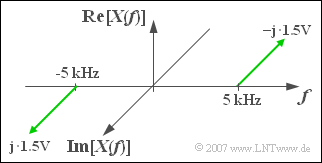
$\text{Beispiel 4:}$ Das Bild zeigt die rein imaginäre Spektralfunktion einer Sinusschwingung $x(t)$ mit
- Amplitude $B = 3 \;{\rm V},$
- Frequenz $f_0 = 5\;{\rm kHz},$
- Phase $\varphi=90^{\circ}$ ⇒ $\phi = -90^{\circ}$.
$\text{Bitte beachten Sie}$:
- Bei der positiven Frequenz $(f = +f_0)$ ist der Imaginärteil negativ.
- Bei der negativen Frequenz $(f = -f_0)$ ergibt sich ein positiver Imaginärteil.
Bei Überlagerung von Cosinus– und Sinusanteil entsprechend der Beziehung
- $$x(t)=A \cdot \cos(2\pi f_0 t) +B \cdot \sin(2 \pi f_0 t)$$
überlagern sich auch die einzelnen Spektralfunktionen und man erhält:
- $$X(f)=\frac{A+{\rm j} \cdot B}{2}\cdot {\rm \delta} (f+f_0)+\frac{A-{\rm j} \cdot B}{2} \cdot \delta (f-f_0).$$
Mit dem Betrag $C$ und der Phase $\varphi$ lautet diese Fourierkorrespondenz:
- $$x(t)=C\cdot \cos(2\pi f_0 t-\varphi)\ \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ X(f)={C}/{2}\cdot {\rm e}^{{\rm j} \varphi} \cdot \delta(f+f_0) + {C}/{2} \cdot {\rm e}^{\rm{-j} \varphi} \cdot \delta (f-f_0).$$
$\text{Man erkennt:}$ Die Spektralfunktion $X(f)$
- ist nicht nur für positive und negative Frequenzen definiert,
- sondern im Allgemeinen auch noch komplexwertig.
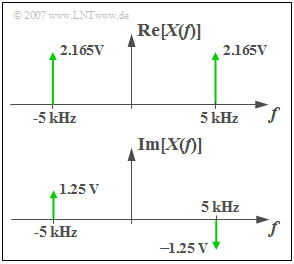
$\text{Beispiel 5:}$ Mit den Parametern $C = 5 \;{\rm V}$, $f_0 = 5\;{\rm kHz}$ und $\varphi=30^{\circ}$ $($im Bogenmaß $\pi/6)$ ergibt sich wegen
- $$2.5 · \cos(30^{\circ}) = 2.165, \hspace{0.3cm} 2.5 · \sin(30^{\circ}) = 1.25$$
der Real- bzw. der Imaginärteil von $X(f)$ gemäß der Grafik:
- $${\rm Re}\big[X(f)\big]=2.165\,{\rm V} \cdot \delta(f+f_0) + 2.165\,{\rm V} \cdot \delta (f-f_0).$$
- $${\rm Im}\big[X(f)\big]=1.25\,{\rm V} \cdot \delta(f+f_0) -1.25\,{\rm V} \cdot \delta (f-f_0).$$
Das Lernvideo
Harmonische Schwingungen verdeutlicht die Eigenschaften harmonischer Schwingungen anhand der so genannten Tonleiter.
Aufgaben zum Kapitel
Aufgabe 2.3: Cosinus- und Sinusanteil
Aufgabe 2.3: Schwingungsparameter