Applets:Physikalisches Signal & Analytisches Signal: Unterschied zwischen den Versionen
K (Guenter verschob die Seite Physikalisches Signal und Analytisches Signal nach Physikalisches Signal & Analytisches Signal) |
Höfler (Diskussion | Beiträge) |
||
| (32 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|physAnSignal_en}} [https://en.lntwww.de/Applets:Physical_Signal_%26_Analytic_Signal '''English Applet with English WIKI description'''] |
| − | |||
==Programmbeschreibung== | ==Programmbeschreibung== | ||
<br> | <br> | ||
| − | Dieses Applet zeigt den Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$. Ausgegangen wird stets von einem Bandpass–Signal $x(t)$ mit frequenzdiskretem Spektrum $X(f)$: | + | Dieses Applet zeigt den Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$. Ausgegangen wird stets von einem Bandpass–Signal $x(t)$ mit frequenzdiskretem Spektrum $X(f)$: |
| − | :$$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$ | + | :$$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$ |
Das physikalische Signal $x(t)$ setzt sich also aus drei [[Signaldarstellung/Harmonische_Schwingung|harmonischen Schwingungen]] zusammen, einer Konstellation, die sich zum Beispiel bei der [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#AM-Signale_und_-Spektren_bei_harmonischem_Eingangssignal|Zweiseitenband-Amplitudenmodulation]] des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$ ergibt. Die Nomenklatur ist ebenfalls an diesen Fall angepasst: | Das physikalische Signal $x(t)$ setzt sich also aus drei [[Signaldarstellung/Harmonische_Schwingung|harmonischen Schwingungen]] zusammen, einer Konstellation, die sich zum Beispiel bei der [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#AM-Signale_und_-Spektren_bei_harmonischem_Eingangssignal|Zweiseitenband-Amplitudenmodulation]] des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$ ergibt. Die Nomenklatur ist ebenfalls an diesen Fall angepasst: | ||
* $x_{\rm O}(t)$ bezeichnet das „Obere Seitenband” mit der Amplitude $A_{\rm O}= A_{\rm N}/2$, der Frequenz $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und der Phase $\varphi_{\rm O} = \varphi_{\rm T} + \varphi_{\rm N}$. | * $x_{\rm O}(t)$ bezeichnet das „Obere Seitenband” mit der Amplitude $A_{\rm O}= A_{\rm N}/2$, der Frequenz $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und der Phase $\varphi_{\rm O} = \varphi_{\rm T} + \varphi_{\rm N}$. | ||
| − | *Entsprechend gilt für das „Untere Seitenband” $x_{\rm U}(t)$ mit $f_{\rm U} = f_{\rm T} | + | *Entsprechend gilt für das „Untere Seitenband” $x_{\rm U}(t)$ mit $f_{\rm U} = f_{\rm T} - f_{\rm N}$, $A_{\rm U}= A_{\rm O}$ und $\varphi_{\rm U} = -\varphi_{\rm O}$. |
Das dazugehörige analytische Signal lautet: | Das dazugehörige analytische Signal lautet: | ||
| − | :$$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{ | + | :$$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} |
| − | \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{ | + | \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} |
| − | \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{ | + | \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$ |
[[Datei:Zeigerdiagramm_2a_version2.png|right|frame|Analytische Signal zur Zeit $t=0$]] | [[Datei:Zeigerdiagramm_2a_version2.png|right|frame|Analytische Signal zur Zeit $t=0$]] | ||
| − | Im Programm dargestellt wird $x_+(t)$ als vektorielle Summe dreier Drehzeiger (alle mit positiver Drehrichtung) als violetter Punkt (siehe beispielhafte Grafik für den Startzeitpunkt $t=0$): | + | Im Programm dargestellt wird $x_+(t)$ als vektorielle Summe dreier Drehzeiger (alle mit positiver Drehrichtung ⇒ entgegen dem Uhrzeigersinn) als violetter Punkt (siehe beispielhafte Grafik für den Startzeitpunkt $t=0$): |
| − | *Der (rote) Zeiger des Trägers $x_{\rm T+}(t)$ mit der Länge $A_{\rm T}$ und der Nullphasenlage $\varphi_{\rm T} = 0$ dreht mit konstanter Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}$ (eine Umdrehung in der Zeit $1/f_{\rm T}$. | + | *Der (rote) Zeiger des Trägers $x_{\rm T+}(t)$ mit der Länge $A_{\rm T}$ und der Nullphasenlage $\varphi_{\rm T} = 0$ dreht mit konstanter Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}$ (eine Umdrehung in der Zeit $1/f_{\rm T})$. |
*Der (blaue) Zeiger des Oberen Seitenbandes $x_{\rm O+}(t)$ mit der Länge $A_{\rm O}$ und der Nullphasenlage $\varphi_{\rm O}$ dreht mit der Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}$, also etwas schneller als $x_{\rm T+}(t)$. | *Der (blaue) Zeiger des Oberen Seitenbandes $x_{\rm O+}(t)$ mit der Länge $A_{\rm O}$ und der Nullphasenlage $\varphi_{\rm O}$ dreht mit der Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}$, also etwas schneller als $x_{\rm T+}(t)$. | ||
| Zeile 26: | Zeile 25: | ||
| − | Den zeitlichen Verlauf von $x_+(t)$ bezeichnen wir im Folgenden auch als '''Zeigerdiagramm'''. Der Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$ | + | Den zeitlichen Verlauf von $x_+(t)$ bezeichnen wir im Folgenden auch als '''Zeigerdiagramm'''. Der Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$ ist sehr einfach: |
:$$x(t) = {\rm Re}\big [x_+(t)\big ].$$ | :$$x(t) = {\rm Re}\big [x_+(t)\big ].$$ | ||
| − | + | Die Grafik gilt für $\varphi_{\rm O} = +30^\circ$. Daraus folgt für den Startzeitpunkt $t=0$ der Winkel gegenüber dem Koordinatensystem: $\phi_{\rm O} = -\varphi_{\rm O} = -30^\circ$. Ebenso folgt aus der Nullphasenlage $\varphi_{\rm U} = -30^\circ$ des unteren Seitenbandes für den in der komplexen Ebene zu berücksichtigenden Phasenwinkel: $\phi_{\rm U} = +30^\circ$. | |
| − | + | ||
| + | |||
| + | ''Hinweis:'' Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung. | ||
| − | |||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
<br> | <br> | ||
| + | ===Beschreibungsmöglichkeiten von Bandpass-Signalen=== | ||
[[Datei:Zeigerdiagramm_1a.png|right|frame|Bandpass–Spektrum $X(f)$ |class=fit]] | [[Datei:Zeigerdiagramm_1a.png|right|frame|Bandpass–Spektrum $X(f)$ |class=fit]] | ||
Wir betrachten hier '''Bandpass-Signale''' $x(t)$ mit der Eigenschaft, dass deren Spektren $X(f)$ nicht im Bereich um die Frequenz $f = 0$ liegen, sondern um eine Trägerfrequenz $f_{\rm T}$. Meist kann auch davon ausgegangen werden, dass die Bandbreite $B \ll f_{\rm T}$ ist. | Wir betrachten hier '''Bandpass-Signale''' $x(t)$ mit der Eigenschaft, dass deren Spektren $X(f)$ nicht im Bereich um die Frequenz $f = 0$ liegen, sondern um eine Trägerfrequenz $f_{\rm T}$. Meist kann auch davon ausgegangen werden, dass die Bandbreite $B \ll f_{\rm T}$ ist. | ||
| − | Die Grafik zeigt ein solches Bandpass–Spektrum $X(f)$. Unter der Annahme, dass das zugehörige $x(t)$ ein physikalisches Signal und damit reell ist, ergibt sich für die Spektralfunktion $X(f)$ eine Symmetrie bezüglich der Frequenz $f = 0$. Ist $x(t)$ eine gerade Funktion ⇒ $x(-t)=x(t)$, so ist auch $X(f)$ reell und gerade. | + | Die Grafik zeigt ein solches Bandpass–Spektrum $X(f)$. Unter der Annahme, dass das zugehörige $x(t)$ ein physikalisches Signal und damit reell ist, ergibt sich für die Spektralfunktion $X(f)$ eine Symmetrie bezüglich der Frequenz $f = 0$. Ist $x(t)$ eine gerade Funktion ⇒ $x(-t)=x(+t)$, so ist auch $X(f)$ reell und gerade. |
| + | |||
Neben dem physikalischen Signal $x(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)$ verwendet man zur Beschreibung von Bandpass-Signalen gleichermaßen: | Neben dem physikalischen Signal $x(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)$ verwendet man zur Beschreibung von Bandpass-Signalen gleichermaßen: | ||
*das analytische Signal $x_+(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_+(f)$, wie im nächsten Unterabschnitt beschrieben, | *das analytische Signal $x_+(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_+(f)$, wie im nächsten Unterabschnitt beschrieben, | ||
| − | *das äquivalente Tiefpass–Signal $x_{\rm TP}(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_{\rm TP}(f)$, siehe Applet [[Physikalisches Signal | + | *das äquivalente Tiefpass–Signal $x_{\rm TP}(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_{\rm TP}(f)$, siehe Applet [[Applets:Physikalisches_Signal_%26_Äquivalentes_TP-Signal|Physikalisches Signal und Äquivalentes Tiefpass–Signal]]. |
| + | <br><br> | ||
| + | ===Analytisches Signal – Spektralfunktion=== | ||
| − | |||
| − | |||
Das zum physikalischen Signal $x(t)$ gehörige '''analytische Signal''' $x_+(t)$ ist diejenige Zeitfunktion, deren Spektrum folgende Eigenschaft erfüllt: | Das zum physikalischen Signal $x(t)$ gehörige '''analytische Signal''' $x_+(t)$ ist diejenige Zeitfunktion, deren Spektrum folgende Eigenschaft erfüllt: | ||
| − | [[Datei: | + | [[Datei:Zeigerdiagramm_3a.png|right|frame|Konstruktion der Spektralfunktion $X_+(f)$ |class=fit]] |
| − | $$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot | + | :$$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot |
X(f) \; \hspace{0.2cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} < 0.} }\right.$$ | X(f) \; \hspace{0.2cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} < 0.} }\right.$$ | ||
| − | Die so genannte ''Signumfunktion'' ist dabei für positive Werte von $f$ gleich $+1$ und für negative $f$–Werte gleich $-1$. | + | Die so genannte ''Signumfunktion'' ist dabei für positive Werte von $f$ gleich $+1$ und für negative $f$–Werte gleich $-1$. |
| − | *Der (beidseitige) Grenzwert liefert $\sign(0) = 0$. | + | *Der (beidseitige) Grenzwert liefert $\sign(0) = 0$. |
*Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt. | *Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt. | ||
| − | Aus der Grafik erkennt man die Berechnungsvorschrift für $X_+(f)$: Das | + | Aus der Grafik erkennt man die Berechnungsvorschrift für $X_+(f)$: Das Bandpass–Spektrum $X(f)$ wird |
*bei den positiven Frequenzen verdoppelt, und | *bei den positiven Frequenzen verdoppelt, und | ||
*bei den negativen Frequenzen zu Null gesetzt. | *bei den negativen Frequenzen zu Null gesetzt. | ||
| − | Aufgrund der Unsymmetrie von $X_+(f)$ bezüglich der Frequenz $f = 0$ kann man bereits jetzt schon sagen, dass die Zeitfunktion $x_+(t)$ bis auf | + | |
| + | Aufgrund der Unsymmetrie von $X_+(f)$ bezüglich der Frequenz $f = 0$ kann man bereits jetzt schon sagen, dass die Zeitfunktion $x_+(t)$ bis auf den trivialen Sonderfall $x_+(t)= 0 \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ X_+(f)= 0$ stets komplex ist. | ||
<br clear=all> | <br clear=all> | ||
===Analytisches Signal – Zeitverlauf=== | ===Analytisches Signal – Zeitverlauf=== | ||
An dieser Stelle ist es erforderlich, kurz auf eine weitere Spektraltransformation einzugehen. | An dieser Stelle ist es erforderlich, kurz auf eine weitere Spektraltransformation einzugehen. | ||
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
$\text{Definition:}$ | $\text{Definition:}$ | ||
Für die '''Hilberttransformierte''' $ {\rm H}\left\{x(t)\right\}$ einer Zeitfunktion $x(t)$ gilt: | Für die '''Hilberttransformierte''' $ {\rm H}\left\{x(t)\right\}$ einer Zeitfunktion $x(t)$ gilt: | ||
| − | + | ||
:$$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot | :$$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot | ||
\hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - | \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - | ||
\tau} }\hspace{0.15cm} {\rm d}\tau.$$ | \tau} }\hspace{0.15cm} {\rm d}\tau.$$ | ||
| − | Dieses bestimmte Integral ist nicht auf einfache, herkömmliche Art lösbar, sondern muss mit Hilfe des [https://de.wikipedia.org/wiki/Cauchyscher_Hauptwert Cauchy–Hauptwertsatzes] ausgewertet werden. | + | Dieses bestimmte Integral ist nicht auf einfache, herkömmliche Art lösbar, sondern muss mit Hilfe des [https://de.wikipedia.org/wiki/Cauchyscher_Hauptwert Cauchy–Hauptwertsatzes] ausgewertet werden. |
Entsprechend gilt im Frequenzbereich: | Entsprechend gilt im Frequenzbereich: | ||
| − | :$$Y(f) = {\rm -j \cdot sign}(f) \cdot X(f) \hspace{0.05cm} .$$}} | + | :$$Y(f) = {\rm -j \cdot sign}(f) \cdot X(f) \hspace{0.05cm} .$$}} |
Das obige Ergebnis lässt sich mit dieser Definition wie folgt zusammenfassen: | Das obige Ergebnis lässt sich mit dieser Definition wie folgt zusammenfassen: | ||
*Man erhält aus dem physikalischen BP–Signal $x(t)$ das analytische Signal $x_+(t)$, indem man zu $x(t)$ einen Imaginärteil gemäß der Hilberttransformierten hinzufügt: | *Man erhält aus dem physikalischen BP–Signal $x(t)$ das analytische Signal $x_+(t)$, indem man zu $x(t)$ einen Imaginärteil gemäß der Hilberttransformierten hinzufügt: | ||
| − | + | ||
:$$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$ | :$$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$ | ||
| Zeile 91: | Zeile 94: | ||
*Aus dem analytischen Signal $x_+(t)$ kann das physikalische Bandpass–Signal in einfacher Weise durch Realteilbildung ermittelt werden: | *Aus dem analytischen Signal $x_+(t)$ kann das physikalische Bandpass–Signal in einfacher Weise durch Realteilbildung ermittelt werden: | ||
| − | :$$x(t) = {\rm Re}\ | + | :$$x(t) = {\rm Re}\big[x_+(t)\big] .$$ |
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Das Prinzip der Hilbert–Transformation wird durch die nachfolgende Grafik nochmals verdeutlicht: | ||
| + | *Nach der linken Darstellung $\rm(A)$ kommt man vom physikalischen Signal $x(t)$ zum analytischen Signal $x_+(t)$, indem man einen Imaginärteil ${\rm j} \cdot y(t)$ hinzufügt. | ||
| + | *Hierbei ist $y(t) = {\rm H}\left\{x(t)\right\}$ eine reelle Zeitfunktion, die sich im Spektralbereich durch die Multiplikation des Spektrums $X(f)$ mit ${\rm - j} \cdot \sign(f)$ angeben lässt. | ||
| − | |||
| − | |||
| − | |||
| − | |||
[[Datei:P_ID2729__Sig_T_4_2_S2b_neu.png|center|frame|Zur Verdeutlichung der Hilbert–Transformierten]] | [[Datei:P_ID2729__Sig_T_4_2_S2b_neu.png|center|frame|Zur Verdeutlichung der Hilbert–Transformierten]] | ||
| Zeile 104: | Zeile 108: | ||
===Darstellung der harmonischen Schwingung als analytisches Signal=== | ===Darstellung der harmonischen Schwingung als analytisches Signal=== | ||
| − | Die Spektralfunktion $X(f)$ einer harmonischen Schwingung $x(t) = A \cdot \text{cos}(2\pi | + | Die Spektralfunktion $X(f)$ einer harmonischen Schwingung $x(t) = A \cdot \text{cos}(2\pi f_{\rm T} \cdot t - \varphi)$ besteht bekanntlich aus zwei Diracfunktionen bei den Frequenzen |
* $+f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$, | * $+f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$, | ||
* $-f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$. | * $-f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$. | ||
| Zeile 113: | Zeile 117: | ||
:$$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm | :$$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm | ||
T}) .$$ | T}) .$$ | ||
| − | + | ||
Die dazugehörige Zeitfunktion erhält man durch Anwendung des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatzes]]: | Die dazugehörige Zeitfunktion erhält man durch Anwendung des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatzes]]: | ||
| − | + | ||
:$$x_+(t) = A \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t | :$$x_+(t) = A \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t | ||
\hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | ||
| − | Diese Gleichung beschreibt einen mit konstanter Winkelgeschwindigkeit $\omega_{\rm T} = 2\pi f_{\rm T}$ drehenden Zeiger. | + | Diese Gleichung beschreibt einen mit konstanter Winkelgeschwindigkeit $\omega_{\rm T} = 2\pi f_{\rm T}$ drehenden Zeiger. |
| − | {{GraueBox|TEXT= | + | {{GraueBox|TEXT= |
$\text{Beispiel 2:}$ Aus Darstellungsgründen wird das Koordinatensystem entgegen der üblichen Darstellung um $90^\circ$ gedreht (Realteil nach oben, Imaginärteil nach links). | $\text{Beispiel 2:}$ Aus Darstellungsgründen wird das Koordinatensystem entgegen der üblichen Darstellung um $90^\circ$ gedreht (Realteil nach oben, Imaginärteil nach links). | ||
| Zeile 134: | Zeile 138: | ||
===$x_+(t)$–Darstellung einer Summe aus drei harmonischen Schwingungen=== | ===$x_+(t)$–Darstellung einer Summe aus drei harmonischen Schwingungen=== | ||
| − | In unserem Applet setzen wir stets einen Zeigerverbund aus drei Drehzeigern voraus. Das physikalische Signal lautet: | + | In unserem Applet setzen wir stets einen Zeigerverbund aus drei Drehzeigern voraus. Das physikalische Signal lautet: |
:$$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$ | :$$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$ | ||
| − | * Jede der drei | + | * Jede der drei harmonischen Schwingungen $x_{\rm T}(t)$, $x_{\rm U}(t)$ und $x_{\rm O}(t)$ wird durch eine Amplitude $(A)$, eine Frequenz $(f)$ und einen Phasenwert $(\varphi)$ charakterisiert. |
| − | *Die Indizes sind an das Modulationsverfahren [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Zweiseitenband–Amplitudenmodulation]] angelehnt. „T” steht für „Träger”, „U” für „Unteres Seitenband” und „O” für „Oberes Seitenband”. Entsprechend gilt stets $f_{\rm U} < f_{\rm T}$ und $f_{\rm O} > f_{\rm T}$. Für die | + | *Die Indizes sind an das Modulationsverfahren [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Zweiseitenband–Amplitudenmodulation]] angelehnt. „T” steht für „Träger”, „U” für „Unteres Seitenband” und „O” für „Oberes Seitenband”. Entsprechend gilt stets $f_{\rm U} < f_{\rm T}$ und $f_{\rm O} > f_{\rm T}$. Für die Amplituden und Phasen gibt es keine Einschränkungen. |
| − | + | Das dazugehörige analytische Signal lautet: | |
| − | + | :$$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} | |
| − | + | \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} | |
| − | + | \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 3:}$ | |
| + | Die hier angegebene Konstellation ergibt sich zum Beispiel bei der [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#AM-Signale_und_-Spektren_bei_harmonischem_Eingangssignal|Zweiseitenband-Amplitudenmodulation]] (mit Träger) des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$. Hierauf wird in der Versuchsdurchführung häufiger eingegangen. | ||
| + | [[Datei:Zeigerdiagramm_5.png|center|frame|Spektum $X_+(f)$ des analytischen Signals für verschiedene Phasenkonstellationen |class=fit]] | ||
| − | + | Bei dieser Betrachtungsweise gibt es einige Einschränkungen bezüglich der Programmparameter: | |
| + | * Für die Frequenzen gelte stets $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und $f_{\rm U} = f_{\rm T} - f_{\rm N}$. | ||
| + | *Ohne Verzerrungen sind die Amplitude der Seitenbänder $A_{\rm O}= A_{\rm U}= A_{\rm N}/2$. | ||
| + | *Die jeweiligen Phasenverhältnisse können der Grafik entnommen werden.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Versuchsdurchführung== | ==Versuchsdurchführung== | ||
| − | [[Datei: | + | [[Datei:Zeigerdiagramm_aufgabe_2.png|right]] |
*Wählen Sie zunächst die Aufgabennummer. | *Wählen Sie zunächst die Aufgabennummer. | ||
*Eine Aufgabenbeschreibung wird angezeigt. | *Eine Aufgabenbeschreibung wird angezeigt. | ||
| − | *Parameterwerte sind angepasst. | + | *Alle Parameterwerte sind angepasst. |
| − | *Lösung nach Drücken von „Hide solition”. | + | *Lösung nach Drücken von „Hide solition”. |
Mit der Nummer „0” wird auf die gleichen Einstellung wie beim Programmstart zurückgesetzt und es wird ein Text mit weiteren Erläuterungen zum Applet ausgegeben. | Mit der Nummer „0” wird auf die gleichen Einstellung wie beim Programmstart zurückgesetzt und es wird ein Text mit weiteren Erläuterungen zum Applet ausgegeben. | ||
| + | <br clear=all> | ||
| − | Im Folgenden bezeichnet $\rm Grün$ das Untere Seitenband ⇒ $\big (A_{\rm U}, f_{\rm U}, \varphi_{\rm U}\big )$, | + | Im Folgenden bezeichnet $\rm Grün$ das Untere Seitenband ⇒ $\big (A_{\rm U}, f_{\rm U}, \varphi_{\rm U}\big )$, |
| − | $\rm Rot$ den Träger ⇒ $\big (A_{\rm T}, f_{\rm T}, \varphi_{\rm T}\big )$ und | + | $\rm Rot$ den Träger ⇒ $\big (A_{\rm T}, f_{\rm T}, \varphi_{\rm T}\big )$ und |
| − | $\rm Blau$ das Obere Seitenband ⇒ $\big (A_{\rm O}, f_{\rm O}, \varphi_{\rm O}\big )$. | + | $\rm Blau$ das Obere Seitenband ⇒ $\big (A_{\rm O}, f_{\rm O}, \varphi_{\rm O}\big )$. |
| − | + | ||
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
| − | '''(1)''' Betrachten und interpretieren Sie das analytische Signal $x_+(t)$ für $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1.5\ \text{V}, \ f_{\rm T} = 50 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$. Außerdem gelte $A_{\rm U} = A_{\rm O} = 0$. | + | '''(1)''' Betrachten und interpretieren Sie das analytische Signal $x_+(t)$ für $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1.5\ \text{V}, \ f_{\rm T} = 50 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$. Außerdem gelte $A_{\rm U} = A_{\rm O} = 0$. |
:Welche Signalwerte $x_+(t)$ ergeben sich für $t = 0$, $t = 5 \ \rm µ s$ und $t = 20 \ \rm µ s$? Wie groß sind die entsprechenden Signalwerte von $x(t)$? }} | :Welche Signalwerte $x_+(t)$ ergeben sich für $t = 0$, $t = 5 \ \rm µ s$ und $t = 20 \ \rm µ s$? Wie groß sind die entsprechenden Signalwerte von $x(t)$? }} | ||
| − | :: Für ein Cosinussignal gilt $x_+(t= 0) = A_{\rm T} = 1.5\ \text{V}$. Danach dreht $x_+(t)$ in mathematisch positiver Richtung (eine Umdrehung pro Periodendauer $T_0 = 1/f_{\rm T}$): | + | :: Für ein Cosinussignal gilt $x_+(t= 0) = A_{\rm T} = 1.5\ \text{V}$. Danach dreht $x_+(t)$ in mathematisch positiver Richtung (eine Umdrehung pro Periodendauer $T_0 = 1/f_{\rm T}$): |
| − | |||
| − | |||
| − | |||
| + | :: $x_+(t= 20 \ {\rm µ s}) = x_+(t= 0) = 1.5\ \text{V}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}x(t= 20 \ {\rm µ s}) = 1.5\ \text{V,}$ | ||
| + | :: $x_+(t= 5 \ {\rm µ s}) = {\rm j} \cdot 1.5\ \text{V}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}x(t= 5 \ {\rm µ s}) = {\rm Re}[x_+(t= 5 \ {\rm µ s})] = 0$. | ||
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
'''(2)''' Wie ändern sich die Verhältnisse für $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1.0\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 90^\circ$?}} | '''(2)''' Wie ändern sich die Verhältnisse für $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1.0\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 90^\circ$?}} | ||
::Das Signal $x(t)$ ist nun ein Sinussignal mit kleinerer Amplitude. Das analytische Signal startet nun wegen $\varphi_{\rm T} = 90^\circ$ ⇒ $\phi_{\rm T} = -90^\circ$ bei $x_+(t= 0) = -{\rm j} \cdot A_{\rm T}$. Danach dreht $x_+(t)$ wieder in mathematisch positiver Richtung, aber wegen $T_0 = 10 \ \rm µ s$ doppelt so schnell als bei $\rm (1)$. | ::Das Signal $x(t)$ ist nun ein Sinussignal mit kleinerer Amplitude. Das analytische Signal startet nun wegen $\varphi_{\rm T} = 90^\circ$ ⇒ $\phi_{\rm T} = -90^\circ$ bei $x_+(t= 0) = -{\rm j} \cdot A_{\rm T}$. Danach dreht $x_+(t)$ wieder in mathematisch positiver Richtung, aber wegen $T_0 = 10 \ \rm µ s$ doppelt so schnell als bei $\rm (1)$. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | {{BlaueBox|TEXT= | + | '''(3)''' Nun gelte $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.15cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = 0^\circ$, $\text{Blau:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 0^\circ$. |
| − | '''(3)''' Nun gelte $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.15cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = 0^\circ$, $\text{Blau:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 0^\circ$. | ||
:Betrachten und interpretieren Sie das physikalische Signal $x(t)$ das analytische Signal $x_+(t)$.}} | :Betrachten und interpretieren Sie das physikalische Signal $x(t)$ das analytische Signal $x_+(t)$.}} | ||
| − | ::Das Signal $x(t)$ ergibt sich bei der Zweiseitenband–Amplitudenmodulation '''(ZSB–AM)''' des Nachrichtensignals $A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$ mit $A_{\rm N} = 0.8\ \text{V}$, $f_{\rm N} = 20\ \text{kHz}$. Der Träger $x_{\rm T}(t)$ mit $f_{\rm T} = 100\ \text{kHz}$ ist ebenfalls cosinusförmig. Der Modulationsgrad ist $m = A_{\rm N}/A_{\rm T} = 0.8$ und die Periodendauer $T_{\rm 0} = 50\ \text{µs}$. | + | ::Das Signal $x(t)$ ergibt sich bei der Zweiseitenband–Amplitudenmodulation '''(ZSB–AM)''' des Nachrichtensignals $A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$ mit $A_{\rm N} = 0.8\ \text{V}$, $f_{\rm N} = 20\ \text{kHz}$. Der Träger $x_{\rm T}(t)$ mit $f_{\rm T} = 100\ \text{kHz}$ ist ebenfalls cosinusförmig. Der Modulationsgrad ist $m = A_{\rm N}/A_{\rm T} = 0.8$ und die Periodendauer $T_{\rm 0} = 50\ \text{µs}$. |
::Im Zeigerdiagramm dreht sich der (rote) Träger schneller als das (grüne) Untere Seitenband und langsamer als das (blaue) Obere Seitenband. Das analytische Signal $x_+(t)$ ergibt sich als die geometrische Summe der drei rotierenden Zeiger. Es scheint so, als würde der blaue Zeiger dem Träger vorauseilen und der grüne Zeiger dem Träger nachlaufen. | ::Im Zeigerdiagramm dreht sich der (rote) Träger schneller als das (grüne) Untere Seitenband und langsamer als das (blaue) Obere Seitenband. Das analytische Signal $x_+(t)$ ergibt sich als die geometrische Summe der drei rotierenden Zeiger. Es scheint so, als würde der blaue Zeiger dem Träger vorauseilen und der grüne Zeiger dem Träger nachlaufen. | ||
| + | {{BlaueBox|TEXT= | ||
| + | '''(4)''' Es gelten weiter die Einstellungen der Aufgabe '''(3)'''. Welche Signalwerte ergeben sich bei $t=0$, $t=2.5 \ \rm µ s$, $t= 5 \ \rm µ s$ und $t=10 \ \rm µ s$? }} | ||
| − | + | ::Zur Zeit $t=0$ liegen alle Zeiger in Richtung der reellen Achse, so dass $x(t=0) = {\rm Re}\big [x+(t= 0)\big] = A_{\rm U} + A_{\rm T} + A_{\rm O} = 1.8\ \text{V}$ gilt. | |
| − | |||
| − | |||
| − | ::Zur Zeit $t=0$ liegen alle Zeiger in Richtung der reellen Achse, so dass $x(t=0) = {\rm Re}\big [x+(t= 0)\big] = A_{\rm U} + A_{\rm T} + A_{\rm O} = 1.8\ \text{V}$ gilt. | ||
::Bis zur Zeit $t=2.5 \ \rm µ s$ hat sich der rote Träger um $90^\circ$ gedreht, der blaue Zeiger um $108^\circ$ und der grüne um $72^\circ$. Es gilt $x(t=2.5 \ \rm µ s) = {\rm Re}\big [x_+(t= 2.5 \ \rm µ s)\big] = 0$, da nun der Zeigerverbund in Richtung der imaginären Achse zeigt. Die weiteren gesuchten Signalwerte sind $x(t=5 \ \rm µ s) = {\rm Re}\big [x_+(t= 5 \ \rm µ s)\big] = -1.647\ \text{V}$ und $x(t=10 \ \rm µ s) = {\rm Re}\big [x_+(t= 10 \ \rm µ s)\big] = 1.247\ \text{V}$. | ::Bis zur Zeit $t=2.5 \ \rm µ s$ hat sich der rote Träger um $90^\circ$ gedreht, der blaue Zeiger um $108^\circ$ und der grüne um $72^\circ$. Es gilt $x(t=2.5 \ \rm µ s) = {\rm Re}\big [x_+(t= 2.5 \ \rm µ s)\big] = 0$, da nun der Zeigerverbund in Richtung der imaginären Achse zeigt. Die weiteren gesuchten Signalwerte sind $x(t=5 \ \rm µ s) = {\rm Re}\big [x_+(t= 5 \ \rm µ s)\big] = -1.647\ \text{V}$ und $x(t=10 \ \rm µ s) = {\rm Re}\big [x_+(t= 10 \ \rm µ s)\big] = 1.247\ \text{V}$. | ||
| − | ::Für $x_+(t)$ ergibt sich ein spiralförmiger Verlauf, abwechselnd mit kleiner werdenem Radius und anschließend mit größerem Radius. | + | ::Für $x_+(t)$ ergibt sich ein spiralförmiger Verlauf, abwechselnd mit kleiner werdenem Radius und anschließend mit größerem Radius. |
| − | + | {{BlaueBox|TEXT= | |
| − | |||
| − | {{BlaueBox|TEXT= | ||
'''(5)''' Wie müssen die Phasenparameter $\varphi_{\rm T}$, $\varphi_{\rm U}$ und $\varphi_{\rm O}$ eingestellt werden, wenn sowohl der Träger $x_{\rm T}(t)$ als auch das Nachrichtensignal $x_{\rm N}(t)$ sinusförmig verlaufen?}} | '''(5)''' Wie müssen die Phasenparameter $\varphi_{\rm T}$, $\varphi_{\rm U}$ und $\varphi_{\rm O}$ eingestellt werden, wenn sowohl der Träger $x_{\rm T}(t)$ als auch das Nachrichtensignal $x_{\rm N}(t)$ sinusförmig verlaufen?}} | ||
::Die Parameterwahl $\varphi_{\rm T} = \varphi_{\rm U} = \varphi_{\rm O}=90^\circ$ beschreibt die Signale $x_{\rm T}(t) = A_{\rm T}\cdot \sin\left(2\pi f_{\rm T}\cdot t\right)$ und $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$. Soll zusätzlich die Nachricht $x_{\rm N}(t)$ sinusförmig verlaufen, so muss $\varphi_{\rm O}=\varphi_{\rm T} - 90^\circ = 0$ und $\varphi_{\rm U}=\varphi_{\rm T} + 90^\circ = 180^\circ$ eingestellt werden. | ::Die Parameterwahl $\varphi_{\rm T} = \varphi_{\rm U} = \varphi_{\rm O}=90^\circ$ beschreibt die Signale $x_{\rm T}(t) = A_{\rm T}\cdot \sin\left(2\pi f_{\rm T}\cdot t\right)$ und $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$. Soll zusätzlich die Nachricht $x_{\rm N}(t)$ sinusförmig verlaufen, so muss $\varphi_{\rm O}=\varphi_{\rm T} - 90^\circ = 0$ und $\varphi_{\rm U}=\varphi_{\rm T} + 90^\circ = 180^\circ$ eingestellt werden. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | {{BlaueBox|TEXT= | ||
'''(6)''' Es gelten die Einstellungen der Aufgabe '''(3)''' mit Ausnahme von $A_{\rm T} = 0.6\ \text{V}$. Welches Modulationsverfahren wird hiermit beschrieben? | '''(6)''' Es gelten die Einstellungen der Aufgabe '''(3)''' mit Ausnahme von $A_{\rm T} = 0.6\ \text{V}$. Welches Modulationsverfahren wird hiermit beschrieben? | ||
: Welche Konsequenzen ergeben sich hieraus? Was ändert sich mit $A_{\rm T} = 0$? }} | : Welche Konsequenzen ergeben sich hieraus? Was ändert sich mit $A_{\rm T} = 0$? }} | ||
| − | ::Es handelt sich um eine '''ZSB–AM mit Träger''' mit dem Modulationsgrad $m=0.8/0.6 = 1.333$. Für $m > 1$ ist allerdings eine [[Modulationsverfahren/Synchrondemodulation|Synchrondemodulation]] erforderlich. [[Modulationsverfahren/Hüllkurvendemodulation|Hüllkurvendemodulation]] funktioniert nicht mehr. | + | ::Es handelt sich um eine '''ZSB–AM mit Träger''' mit dem Modulationsgrad $m=0.8/0.6 = 1.333$. Für $m > 1$ ist allerdings eine [[Modulationsverfahren/Synchrondemodulation|Synchrondemodulation]] erforderlich. [[Modulationsverfahren/Hüllkurvendemodulation|Hüllkurvendemodulation]] funktioniert nicht mehr. Ein Grund hierfür ist, dass nun die Nulldurchgänge von $x(t)$ nicht mehr im äquidistanten Abstand von $5\ \rm µ s$ auftreten ⇒ zusätzliche Phasenmodulation. |
| − | |||
| − | |||
| + | ::Mit $A_{\rm T} = 0$ ⇒ $m \to \infty$ ergibt sich eine '''ZSB–AM ohne Träger'''. Auch hierfür benötigt man unbedingt die Synchrondemodulation. | ||
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
| − | '''(7)''' | + | '''(7)''' Nun gelte $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.15cm} A_{\rm U} = 0$, $\text{Blau:} \hspace{0.15cm} A_{\rm O} = 0.8\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 90^\circ$. |
| − | : | + | :Welche Konstellation wird hiermit beschrieben? Welche Figur ergibt sich für das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$? ⇒ „Ortskurve”? <br>Was ändert sich mit $A_{\rm U} = 0.8\ \text{V}$ und $A_{\rm O} = 0$?}} |
| − | ::In beiden Fällen handelt es sich um eine [[Modulationsverfahren/Einseitenbandmodulation|Einseitenbandmodulation]] '''(ESB–AM)''' mit dem Modulationsgrad $\mu = 0.8$ (bei ESB bezeichnen wir den Modulationsgrad mit $\mu$ anstelle von $m$). Das Trägersignal ist cosinusförmig und das Nachrichtensignal sinusförmig. | + | ::In beiden Fällen handelt es sich um eine [[Modulationsverfahren/Einseitenbandmodulation|Einseitenbandmodulation]] '''(ESB–AM)''' mit dem Modulationsgrad $\mu = 0.8$ (bei ESB bezeichnen wir den Modulationsgrad mit $\mu$ anstelle von $m$). Das Trägersignal ist cosinusförmig und das Nachrichtensignal sinusförmig. Das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$ hat in der komplexen Ebene einen kreisförmigen Verlauf. |
::Mit $A_{\rm O} = 0.8\ \text{V}$, $A_{\rm U} = 0$ handelt es sich um eine OSB–Modulation. Der grüne Zeiger fehlt und der blaue Zeiger dreht im Vergleich zum roten Träger schneller. | ::Mit $A_{\rm O} = 0.8\ \text{V}$, $A_{\rm U} = 0$ handelt es sich um eine OSB–Modulation. Der grüne Zeiger fehlt und der blaue Zeiger dreht im Vergleich zum roten Träger schneller. | ||
| Zeile 350: | Zeile 236: | ||
::Mit $A_{\rm U} = 0.8\ \text{V}$, $A_{\rm O} = 0$ handelt es sich um eine USB–Modulation. Der blaue Zeiger fehlt und der grüne Zeiger dreht im Vergleich zum roten Träger langsamer. | ::Mit $A_{\rm U} = 0.8\ \text{V}$, $A_{\rm O} = 0$ handelt es sich um eine USB–Modulation. Der blaue Zeiger fehlt und der grüne Zeiger dreht im Vergleich zum roten Träger langsamer. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | {{BlaueBox|TEXT= | ||
'''(8)''' Es gelte $\text{Rot:} \hspace{0.05cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.05cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = -90^\circ$, $\text{Blau:} \hspace{0.05cm} A_{\rm O} = 0.2\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = +90^\circ$. | '''(8)''' Es gelte $\text{Rot:} \hspace{0.05cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.05cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = -90^\circ$, $\text{Blau:} \hspace{0.05cm} A_{\rm O} = 0.2\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = +90^\circ$. | ||
| − | : | + | :Welche Konstellation könnte hiermit beschrieben werden? Welche Figur ergibt sich für das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$? ⇒ „Ortskurve”?}} |
| − | ::Es könnte eine ZSB–AM eines Sinussignals mit cosinusförmigem Träger und Modulationsgrad $m=0.8$ vorliegen, bei dem das Obere Seitenband um den Faktor $2$ gedämpft ist. Das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$ hat in der komplexen Ebene einen elliptischen Verlauf. | + | ::Es könnte eine ZSB–AM eines Sinussignals mit cosinusförmigem Träger und Modulationsgrad $m=0.8$ wie in '''(3)''' vorliegen, bei dem aber das Obere Seitenband um den Faktor $2$ gedämpft ist. Das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$ hat in der komplexen Ebene einen elliptischen Verlauf. |
==Zur Handhabung des Applets== | ==Zur Handhabung des Applets== | ||
| − | |||
<br> | <br> | ||
| − | + | [[Datei:Zeigerdiagramm_abzug.png|right|frame|Bildschirmabzug der englischen Version]] | |
| − | + | * Die roten Parameter $(A_{\rm T}, \ f_{\rm T}, \ \varphi_{\rm T})$ und der rote Zeiger kennzeichnen den '''T'''räger. | |
| + | * Die grünen Parameter $(A_{\rm U}, \ f_{\rm U} < f_{\rm T}, \ \varphi_{\rm U})$ kennzeichnen das '''U'''ntere Seitenband. | ||
| + | * Die blauen Parameter $(A_{\rm O}, \ f_{\rm O} > f_{\rm T}, \ \varphi_{\rm O})$ kennzeichnen das '''O'''bere Seitenband. | ||
| + | *Alle Zeiger drehen in mathematisch positiver Richtung (entgegen dem Uhrzeigersinn). | ||
| − | |||
| − | + | Bedeutung der Buchstaben in nebenstehender Grafik: | |
| − | '''( | + | '''(A)''' Grafikfeld für das analytische Signal $x_{\rm +}(t)$ |
| − | '''( | + | '''(B)''' Grafikfeld für das physikalische Signal $x(t)$ |
| − | '''( | + | '''(C)''' Parametereingabe per Slider: Amplituden, Frequenzen, Phasenwerte |
| − | '''( | + | '''(D)''' Bedienelemente: Start – Step – Pause/Continue – Reset |
| − | '''( | + | '''(E)''' Geschwindigkeit der Animation: „Speed” ⇒ Werte: 1, 2 oder 3 |
| − | '''( | + | '''(F)''' „Trace” ⇒ Ein oder Aus, Spur der komplexen Signalwerte $x_{\rm +}(t)$ |
| − | '''( | + | '''(G)''' Numerikausgabe der Zeit $t$ und der Signalwerte ${\rm Re}[x_{\rm +}(t)] = x(t)$ und ${\rm Im}[x_{\rm +}(t)]$ |
| − | '''( | + | '''(H)''' Variationsmöglichkeiten für die grafische Darstellung |
| − | |||
| − | |||
$\hspace{1.5cm}$Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen) | $\hspace{1.5cm}$Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen) | ||
$\hspace{1.5cm}$Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$” | $\hspace{1.5cm}$Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$” | ||
| − | + | '''(I)''' Bereich für die Versuchsdurchführung: Aufgabenauswahl und Aufgabenstellung | |
| − | + | '''(J)''' Bereich für die Versuchsdurchführung: Musterlösung | |
| − | |||
| + | In allen Applets oben rechts: Veränderbare grafische Oberflächengestaltung ⇒ '''Theme''': | ||
| + | * Dark: schwarzer Hintergrund (wird von den Autoren empfohlen) | ||
| + | * Bright: weißer Hintergrund (empfohlen für Beamer und Ausdrucke) | ||
| + | * Deuteranopia: für Nutzer mit ausgeprägter Grün–Sehschwäche | ||
| + | * Protanopia: für Nutzer mit ausgeprägter Rot–Sehschwäche | ||
| + | <br clear=all> | ||
==Über die Autoren== | ==Über die Autoren== | ||
| − | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | + | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. |
| − | *Die erste Version wurde 2005 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende# | + | *Die erste Version wurde 2005 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Ji_Li_.28Bachelorarbeit_EI_2003.2C_Diplomarbeit_EI_2005.29|Ji Li]] im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| − | *2018 wurde dieses Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende# | + | *2018 wurde dieses Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Xiaohan_Liu_.28Bachelorarbeit_2018.29|Xiaohan Liu]] im Rahmen ihrer Bachelorarbeit (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_LÜT-Angehörige#Dr.-Ing._Tasn.C3.A1d_Kernetzky_.28bei_L.C3.9CT_von_2014-2022.29|Tasnád Kernetzky]]) neu gestaltet und erweitert. |
| + | |||
| + | |||
| + | Die Fertigstellung dieses Applets wurde durch [https://www.ei.tum.de/studium/studienzuschuesse/ Studienzuschüsse] der Fakultät EI der TU München ermöglicht. Wir bedanken uns. | ||
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|physAnSignal_en}} [https://en.lntwww.de/Applets:Physical_Signal_%26_Analytic_Signal '''English Applet with English WIKI description'''] |
| − | + | <br><br> | |
| − | |||
Aktuelle Version vom 26. Oktober 2023, 10:46 Uhr
Applet in neuem Tab öffnen English Applet with English WIKI description
Inhaltsverzeichnis
Programmbeschreibung
Dieses Applet zeigt den Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$. Ausgegangen wird stets von einem Bandpass–Signal $x(t)$ mit frequenzdiskretem Spektrum $X(f)$:
- $$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$
Das physikalische Signal $x(t)$ setzt sich also aus drei harmonischen Schwingungen zusammen, einer Konstellation, die sich zum Beispiel bei der Zweiseitenband-Amplitudenmodulation des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$ ergibt. Die Nomenklatur ist ebenfalls an diesen Fall angepasst:
- $x_{\rm O}(t)$ bezeichnet das „Obere Seitenband” mit der Amplitude $A_{\rm O}= A_{\rm N}/2$, der Frequenz $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und der Phase $\varphi_{\rm O} = \varphi_{\rm T} + \varphi_{\rm N}$.
- Entsprechend gilt für das „Untere Seitenband” $x_{\rm U}(t)$ mit $f_{\rm U} = f_{\rm T} - f_{\rm N}$, $A_{\rm U}= A_{\rm O}$ und $\varphi_{\rm U} = -\varphi_{\rm O}$.
Das dazugehörige analytische Signal lautet:
- $$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$
Im Programm dargestellt wird $x_+(t)$ als vektorielle Summe dreier Drehzeiger (alle mit positiver Drehrichtung ⇒ entgegen dem Uhrzeigersinn) als violetter Punkt (siehe beispielhafte Grafik für den Startzeitpunkt $t=0$):
- Der (rote) Zeiger des Trägers $x_{\rm T+}(t)$ mit der Länge $A_{\rm T}$ und der Nullphasenlage $\varphi_{\rm T} = 0$ dreht mit konstanter Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}$ (eine Umdrehung in der Zeit $1/f_{\rm T})$.
- Der (blaue) Zeiger des Oberen Seitenbandes $x_{\rm O+}(t)$ mit der Länge $A_{\rm O}$ und der Nullphasenlage $\varphi_{\rm O}$ dreht mit der Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}$, also etwas schneller als $x_{\rm T+}(t)$.
- Der (grüne) Zeiger des Unteren Seitenbandes $x_{\rm U+}(t)$ mit der Länge $A_{\rm U}$ und der Nullphasenlage $\varphi_{\rm U}$ dreht mit der Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}$, also etwas langsamer als $x_{\rm T+}(t)$.
Den zeitlichen Verlauf von $x_+(t)$ bezeichnen wir im Folgenden auch als Zeigerdiagramm. Der Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$ ist sehr einfach:
- $$x(t) = {\rm Re}\big [x_+(t)\big ].$$
Die Grafik gilt für $\varphi_{\rm O} = +30^\circ$. Daraus folgt für den Startzeitpunkt $t=0$ der Winkel gegenüber dem Koordinatensystem: $\phi_{\rm O} = -\varphi_{\rm O} = -30^\circ$. Ebenso folgt aus der Nullphasenlage $\varphi_{\rm U} = -30^\circ$ des unteren Seitenbandes für den in der komplexen Ebene zu berücksichtigenden Phasenwinkel: $\phi_{\rm U} = +30^\circ$.
Hinweis: Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung.
Theoretischer Hintergrund
Beschreibungsmöglichkeiten von Bandpass-Signalen
Wir betrachten hier Bandpass-Signale $x(t)$ mit der Eigenschaft, dass deren Spektren $X(f)$ nicht im Bereich um die Frequenz $f = 0$ liegen, sondern um eine Trägerfrequenz $f_{\rm T}$. Meist kann auch davon ausgegangen werden, dass die Bandbreite $B \ll f_{\rm T}$ ist.
Die Grafik zeigt ein solches Bandpass–Spektrum $X(f)$. Unter der Annahme, dass das zugehörige $x(t)$ ein physikalisches Signal und damit reell ist, ergibt sich für die Spektralfunktion $X(f)$ eine Symmetrie bezüglich der Frequenz $f = 0$. Ist $x(t)$ eine gerade Funktion ⇒ $x(-t)=x(+t)$, so ist auch $X(f)$ reell und gerade.
Neben dem physikalischen Signal $x(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)$ verwendet man zur Beschreibung von Bandpass-Signalen gleichermaßen:
- das analytische Signal $x_+(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_+(f)$, wie im nächsten Unterabschnitt beschrieben,
- das äquivalente Tiefpass–Signal $x_{\rm TP}(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_{\rm TP}(f)$, siehe Applet Physikalisches Signal und Äquivalentes Tiefpass–Signal.
Analytisches Signal – Spektralfunktion
Das zum physikalischen Signal $x(t)$ gehörige analytische Signal $x_+(t)$ ist diejenige Zeitfunktion, deren Spektrum folgende Eigenschaft erfüllt:
- $$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot X(f) \; \hspace{0.2cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} < 0.} }\right.$$
Die so genannte Signumfunktion ist dabei für positive Werte von $f$ gleich $+1$ und für negative $f$–Werte gleich $-1$.
- Der (beidseitige) Grenzwert liefert $\sign(0) = 0$.
- Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt.
Aus der Grafik erkennt man die Berechnungsvorschrift für $X_+(f)$: Das Bandpass–Spektrum $X(f)$ wird
- bei den positiven Frequenzen verdoppelt, und
- bei den negativen Frequenzen zu Null gesetzt.
Aufgrund der Unsymmetrie von $X_+(f)$ bezüglich der Frequenz $f = 0$ kann man bereits jetzt schon sagen, dass die Zeitfunktion $x_+(t)$ bis auf den trivialen Sonderfall $x_+(t)= 0 \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ X_+(f)= 0$ stets komplex ist.
Analytisches Signal – Zeitverlauf
An dieser Stelle ist es erforderlich, kurz auf eine weitere Spektraltransformation einzugehen.
$\text{Definition:}$ Für die Hilberttransformierte $ {\rm H}\left\{x(t)\right\}$ einer Zeitfunktion $x(t)$ gilt:
- $$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau} }\hspace{0.15cm} {\rm d}\tau.$$
Dieses bestimmte Integral ist nicht auf einfache, herkömmliche Art lösbar, sondern muss mit Hilfe des Cauchy–Hauptwertsatzes ausgewertet werden.
Entsprechend gilt im Frequenzbereich:
- $$Y(f) = {\rm -j \cdot sign}(f) \cdot X(f) \hspace{0.05cm} .$$
Das obige Ergebnis lässt sich mit dieser Definition wie folgt zusammenfassen:
- Man erhält aus dem physikalischen BP–Signal $x(t)$ das analytische Signal $x_+(t)$, indem man zu $x(t)$ einen Imaginärteil gemäß der Hilberttransformierten hinzufügt:
- $$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$
- $\text{H}\{x(t)\}$ verschwindet nur für den Fall $x(t) = \rm const.$ ⇒ Gleichsignal. Bei allen anderen Signalformen ist somit das analytische Signal $x_+(t)$ komplex.
- Aus dem analytischen Signal $x_+(t)$ kann das physikalische Bandpass–Signal in einfacher Weise durch Realteilbildung ermittelt werden:
- $$x(t) = {\rm Re}\big[x_+(t)\big] .$$
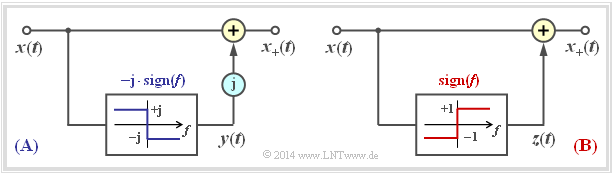
$\text{Beispiel 1:}$ Das Prinzip der Hilbert–Transformation wird durch die nachfolgende Grafik nochmals verdeutlicht:
- Nach der linken Darstellung $\rm(A)$ kommt man vom physikalischen Signal $x(t)$ zum analytischen Signal $x_+(t)$, indem man einen Imaginärteil ${\rm j} \cdot y(t)$ hinzufügt.
- Hierbei ist $y(t) = {\rm H}\left\{x(t)\right\}$ eine reelle Zeitfunktion, die sich im Spektralbereich durch die Multiplikation des Spektrums $X(f)$ mit ${\rm - j} \cdot \sign(f)$ angeben lässt.
Die rechte Darstellung $\rm(B)$ ist äquivalent zu $\rm(A)$. Nun gilt $x_+(t) = x(t) + z(t)$ mit der rein imaginären Funktion $z(t)$. Ein Vergleich der beiden Bilder zeigt, dass tatsächlich $z(t) = {\rm j} \cdot y(t)$ ist.
Darstellung der harmonischen Schwingung als analytisches Signal
Die Spektralfunktion $X(f)$ einer harmonischen Schwingung $x(t) = A \cdot \text{cos}(2\pi f_{\rm T} \cdot t - \varphi)$ besteht bekanntlich aus zwei Diracfunktionen bei den Frequenzen
- $+f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$,
- $-f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$.
Somit lautet das Spektrum des analytischen Signals (also ohne die Diracfunktion bei der Frequenz $f =-f_{\rm T}$, aber Verdoppelung bei $f =+f_{\rm T}$):
- $$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm T}) .$$
Die dazugehörige Zeitfunktion erhält man durch Anwendung des Verschiebungssatzes:
- $$x_+(t) = A \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$
Diese Gleichung beschreibt einen mit konstanter Winkelgeschwindigkeit $\omega_{\rm T} = 2\pi f_{\rm T}$ drehenden Zeiger.
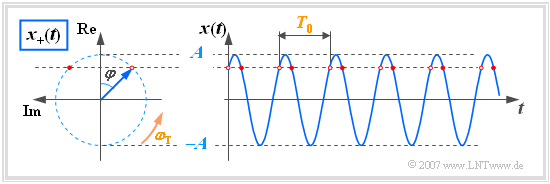
$\text{Beispiel 2:}$ Aus Darstellungsgründen wird das Koordinatensystem entgegen der üblichen Darstellung um $90^\circ$ gedreht (Realteil nach oben, Imaginärteil nach links).
Anhand dieser Grafik sind folgende Aussagen möglich:
- Zum Startzeitpunkt $t = 0$ liegt der Zeiger der Länge $A$ (Signalamplitude) mit dem Winkel $-\varphi$ in der komplexen Ebene. Im gezeichneten Beispiel gilt $\varphi = 45^\circ$.
- Für Zeiten $t > 0$ dreht der Zeiger mit konstanter Winkelgeschwindigkeit (Kreisfrequenz) $\omega_{\rm T}$ in mathematisch positiver Richtung, das heißt entgegen dem Uhrzeigersinn.
- Die Spitze des Zeigers liegt somit stets auf einem Kreis mit Radius $A$ und benötigt für eine Umdrehung genau die Zeit $T_0$, also die Periodendauer der harmonischen Schwingung $x(t)$.
- Die Projektion des analytischen Signals $x_+(t)$ auf die reelle Achse, durch rote Punkte markiert, liefert die Augenblickswerte von $x(t)$.
$x_+(t)$–Darstellung einer Summe aus drei harmonischen Schwingungen
In unserem Applet setzen wir stets einen Zeigerverbund aus drei Drehzeigern voraus. Das physikalische Signal lautet:
- $$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$
- Jede der drei harmonischen Schwingungen $x_{\rm T}(t)$, $x_{\rm U}(t)$ und $x_{\rm O}(t)$ wird durch eine Amplitude $(A)$, eine Frequenz $(f)$ und einen Phasenwert $(\varphi)$ charakterisiert.
- Die Indizes sind an das Modulationsverfahren Zweiseitenband–Amplitudenmodulation angelehnt. „T” steht für „Träger”, „U” für „Unteres Seitenband” und „O” für „Oberes Seitenband”. Entsprechend gilt stets $f_{\rm U} < f_{\rm T}$ und $f_{\rm O} > f_{\rm T}$. Für die Amplituden und Phasen gibt es keine Einschränkungen.
Das dazugehörige analytische Signal lautet:
- $$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$
$\text{Beispiel 3:}$ Die hier angegebene Konstellation ergibt sich zum Beispiel bei der Zweiseitenband-Amplitudenmodulation (mit Träger) des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$. Hierauf wird in der Versuchsdurchführung häufiger eingegangen.
Bei dieser Betrachtungsweise gibt es einige Einschränkungen bezüglich der Programmparameter:
- Für die Frequenzen gelte stets $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und $f_{\rm U} = f_{\rm T} - f_{\rm N}$.
- Ohne Verzerrungen sind die Amplitude der Seitenbänder $A_{\rm O}= A_{\rm U}= A_{\rm N}/2$.
- Die jeweiligen Phasenverhältnisse können der Grafik entnommen werden.
Versuchsdurchführung
- Wählen Sie zunächst die Aufgabennummer.
- Eine Aufgabenbeschreibung wird angezeigt.
- Alle Parameterwerte sind angepasst.
- Lösung nach Drücken von „Hide solition”.
Mit der Nummer „0” wird auf die gleichen Einstellung wie beim Programmstart zurückgesetzt und es wird ein Text mit weiteren Erläuterungen zum Applet ausgegeben.
Im Folgenden bezeichnet $\rm Grün$ das Untere Seitenband ⇒ $\big (A_{\rm U}, f_{\rm U}, \varphi_{\rm U}\big )$,
$\rm Rot$ den Träger ⇒ $\big (A_{\rm T}, f_{\rm T}, \varphi_{\rm T}\big )$ und
$\rm Blau$ das Obere Seitenband ⇒ $\big (A_{\rm O}, f_{\rm O}, \varphi_{\rm O}\big )$.
(1) Betrachten und interpretieren Sie das analytische Signal $x_+(t)$ für $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1.5\ \text{V}, \ f_{\rm T} = 50 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$. Außerdem gelte $A_{\rm U} = A_{\rm O} = 0$.
- Welche Signalwerte $x_+(t)$ ergeben sich für $t = 0$, $t = 5 \ \rm µ s$ und $t = 20 \ \rm µ s$? Wie groß sind die entsprechenden Signalwerte von $x(t)$?
- Für ein Cosinussignal gilt $x_+(t= 0) = A_{\rm T} = 1.5\ \text{V}$. Danach dreht $x_+(t)$ in mathematisch positiver Richtung (eine Umdrehung pro Periodendauer $T_0 = 1/f_{\rm T}$):
- $x_+(t= 20 \ {\rm µ s}) = x_+(t= 0) = 1.5\ \text{V}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}x(t= 20 \ {\rm µ s}) = 1.5\ \text{V,}$
- $x_+(t= 5 \ {\rm µ s}) = {\rm j} \cdot 1.5\ \text{V}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}x(t= 5 \ {\rm µ s}) = {\rm Re}[x_+(t= 5 \ {\rm µ s})] = 0$.
(2) Wie ändern sich die Verhältnisse für $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1.0\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 90^\circ$?
- Das Signal $x(t)$ ist nun ein Sinussignal mit kleinerer Amplitude. Das analytische Signal startet nun wegen $\varphi_{\rm T} = 90^\circ$ ⇒ $\phi_{\rm T} = -90^\circ$ bei $x_+(t= 0) = -{\rm j} \cdot A_{\rm T}$. Danach dreht $x_+(t)$ wieder in mathematisch positiver Richtung, aber wegen $T_0 = 10 \ \rm µ s$ doppelt so schnell als bei $\rm (1)$.
(3) Nun gelte $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.15cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = 0^\circ$, $\text{Blau:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 0^\circ$.
- Betrachten und interpretieren Sie das physikalische Signal $x(t)$ das analytische Signal $x_+(t)$.
- Das Signal $x(t)$ ergibt sich bei der Zweiseitenband–Amplitudenmodulation (ZSB–AM) des Nachrichtensignals $A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$ mit $A_{\rm N} = 0.8\ \text{V}$, $f_{\rm N} = 20\ \text{kHz}$. Der Träger $x_{\rm T}(t)$ mit $f_{\rm T} = 100\ \text{kHz}$ ist ebenfalls cosinusförmig. Der Modulationsgrad ist $m = A_{\rm N}/A_{\rm T} = 0.8$ und die Periodendauer $T_{\rm 0} = 50\ \text{µs}$.
- Im Zeigerdiagramm dreht sich der (rote) Träger schneller als das (grüne) Untere Seitenband und langsamer als das (blaue) Obere Seitenband. Das analytische Signal $x_+(t)$ ergibt sich als die geometrische Summe der drei rotierenden Zeiger. Es scheint so, als würde der blaue Zeiger dem Träger vorauseilen und der grüne Zeiger dem Träger nachlaufen.
(4) Es gelten weiter die Einstellungen der Aufgabe (3). Welche Signalwerte ergeben sich bei $t=0$, $t=2.5 \ \rm µ s$, $t= 5 \ \rm µ s$ und $t=10 \ \rm µ s$?
- Zur Zeit $t=0$ liegen alle Zeiger in Richtung der reellen Achse, so dass $x(t=0) = {\rm Re}\big [x+(t= 0)\big] = A_{\rm U} + A_{\rm T} + A_{\rm O} = 1.8\ \text{V}$ gilt.
- Bis zur Zeit $t=2.5 \ \rm µ s$ hat sich der rote Träger um $90^\circ$ gedreht, der blaue Zeiger um $108^\circ$ und der grüne um $72^\circ$. Es gilt $x(t=2.5 \ \rm µ s) = {\rm Re}\big [x_+(t= 2.5 \ \rm µ s)\big] = 0$, da nun der Zeigerverbund in Richtung der imaginären Achse zeigt. Die weiteren gesuchten Signalwerte sind $x(t=5 \ \rm µ s) = {\rm Re}\big [x_+(t= 5 \ \rm µ s)\big] = -1.647\ \text{V}$ und $x(t=10 \ \rm µ s) = {\rm Re}\big [x_+(t= 10 \ \rm µ s)\big] = 1.247\ \text{V}$.
- Für $x_+(t)$ ergibt sich ein spiralförmiger Verlauf, abwechselnd mit kleiner werdenem Radius und anschließend mit größerem Radius.
(5) Wie müssen die Phasenparameter $\varphi_{\rm T}$, $\varphi_{\rm U}$ und $\varphi_{\rm O}$ eingestellt werden, wenn sowohl der Träger $x_{\rm T}(t)$ als auch das Nachrichtensignal $x_{\rm N}(t)$ sinusförmig verlaufen?
- Die Parameterwahl $\varphi_{\rm T} = \varphi_{\rm U} = \varphi_{\rm O}=90^\circ$ beschreibt die Signale $x_{\rm T}(t) = A_{\rm T}\cdot \sin\left(2\pi f_{\rm T}\cdot t\right)$ und $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$. Soll zusätzlich die Nachricht $x_{\rm N}(t)$ sinusförmig verlaufen, so muss $\varphi_{\rm O}=\varphi_{\rm T} - 90^\circ = 0$ und $\varphi_{\rm U}=\varphi_{\rm T} + 90^\circ = 180^\circ$ eingestellt werden.
(6) Es gelten die Einstellungen der Aufgabe (3) mit Ausnahme von $A_{\rm T} = 0.6\ \text{V}$. Welches Modulationsverfahren wird hiermit beschrieben?
- Welche Konsequenzen ergeben sich hieraus? Was ändert sich mit $A_{\rm T} = 0$?
- Es handelt sich um eine ZSB–AM mit Träger mit dem Modulationsgrad $m=0.8/0.6 = 1.333$. Für $m > 1$ ist allerdings eine Synchrondemodulation erforderlich. Hüllkurvendemodulation funktioniert nicht mehr. Ein Grund hierfür ist, dass nun die Nulldurchgänge von $x(t)$ nicht mehr im äquidistanten Abstand von $5\ \rm µ s$ auftreten ⇒ zusätzliche Phasenmodulation.
- Mit $A_{\rm T} = 0$ ⇒ $m \to \infty$ ergibt sich eine ZSB–AM ohne Träger. Auch hierfür benötigt man unbedingt die Synchrondemodulation.
(7) Nun gelte $\text{Rot:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.15cm} A_{\rm U} = 0$, $\text{Blau:} \hspace{0.15cm} A_{\rm O} = 0.8\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 90^\circ$.
- Welche Konstellation wird hiermit beschrieben? Welche Figur ergibt sich für das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$? ⇒ „Ortskurve”?
Was ändert sich mit $A_{\rm U} = 0.8\ \text{V}$ und $A_{\rm O} = 0$?
- In beiden Fällen handelt es sich um eine Einseitenbandmodulation (ESB–AM) mit dem Modulationsgrad $\mu = 0.8$ (bei ESB bezeichnen wir den Modulationsgrad mit $\mu$ anstelle von $m$). Das Trägersignal ist cosinusförmig und das Nachrichtensignal sinusförmig. Das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$ hat in der komplexen Ebene einen kreisförmigen Verlauf.
- Mit $A_{\rm O} = 0.8\ \text{V}$, $A_{\rm U} = 0$ handelt es sich um eine OSB–Modulation. Der grüne Zeiger fehlt und der blaue Zeiger dreht im Vergleich zum roten Träger schneller.
- Mit $A_{\rm U} = 0.8\ \text{V}$, $A_{\rm O} = 0$ handelt es sich um eine USB–Modulation. Der blaue Zeiger fehlt und der grüne Zeiger dreht im Vergleich zum roten Träger langsamer.
(8) Es gelte $\text{Rot:} \hspace{0.05cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Grün:} \hspace{0.05cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = -90^\circ$, $\text{Blau:} \hspace{0.05cm} A_{\rm O} = 0.2\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = +90^\circ$.
- Welche Konstellation könnte hiermit beschrieben werden? Welche Figur ergibt sich für das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$? ⇒ „Ortskurve”?
- Es könnte eine ZSB–AM eines Sinussignals mit cosinusförmigem Träger und Modulationsgrad $m=0.8$ wie in (3) vorliegen, bei dem aber das Obere Seitenband um den Faktor $2$ gedämpft ist. Das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$ hat in der komplexen Ebene einen elliptischen Verlauf.
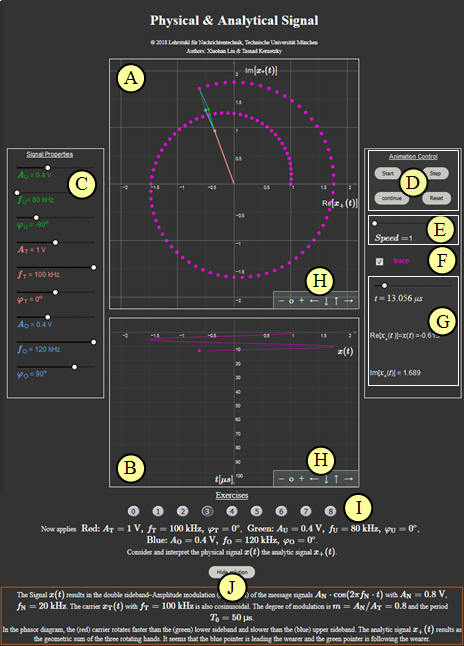
Zur Handhabung des Applets
- Die roten Parameter $(A_{\rm T}, \ f_{\rm T}, \ \varphi_{\rm T})$ und der rote Zeiger kennzeichnen den Träger.
- Die grünen Parameter $(A_{\rm U}, \ f_{\rm U} < f_{\rm T}, \ \varphi_{\rm U})$ kennzeichnen das Untere Seitenband.
- Die blauen Parameter $(A_{\rm O}, \ f_{\rm O} > f_{\rm T}, \ \varphi_{\rm O})$ kennzeichnen das Obere Seitenband.
- Alle Zeiger drehen in mathematisch positiver Richtung (entgegen dem Uhrzeigersinn).
Bedeutung der Buchstaben in nebenstehender Grafik:
(A) Grafikfeld für das analytische Signal $x_{\rm +}(t)$
(B) Grafikfeld für das physikalische Signal $x(t)$
(C) Parametereingabe per Slider: Amplituden, Frequenzen, Phasenwerte
(D) Bedienelemente: Start – Step – Pause/Continue – Reset
(E) Geschwindigkeit der Animation: „Speed” ⇒ Werte: 1, 2 oder 3
(F) „Trace” ⇒ Ein oder Aus, Spur der komplexen Signalwerte $x_{\rm +}(t)$
(G) Numerikausgabe der Zeit $t$ und der Signalwerte ${\rm Re}[x_{\rm +}(t)] = x(t)$ und ${\rm Im}[x_{\rm +}(t)]$
(H) Variationsmöglichkeiten für die grafische Darstellung
$\hspace{1.5cm}$Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
$\hspace{1.5cm}$Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”
(I) Bereich für die Versuchsdurchführung: Aufgabenauswahl und Aufgabenstellung
(J) Bereich für die Versuchsdurchführung: Musterlösung
In allen Applets oben rechts: Veränderbare grafische Oberflächengestaltung ⇒ Theme:
- Dark: schwarzer Hintergrund (wird von den Autoren empfohlen)
- Bright: weißer Hintergrund (empfohlen für Beamer und Ausdrucke)
- Deuteranopia: für Nutzer mit ausgeprägter Grün–Sehschwäche
- Protanopia: für Nutzer mit ausgeprägter Rot–Sehschwäche
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde dieses Programm von Xiaohan Liu im Rahmen ihrer Bachelorarbeit (Betreuer: Tasnád Kernetzky) neu gestaltet und erweitert.
Die Fertigstellung dieses Applets wurde durch Studienzuschüsse der Fakultät EI der TU München ermöglicht. Wir bedanken uns.
Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
Applet in neuem Tab öffnen
English Applet with English WIKI description