Applets:Das Gram-Schmidt-Verfahren: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{LntAppletLink|augendiagramm}} ==Programmbeschreibung== <br> Das Applet verdeutlicht die Augendiagramme für *verschiedene Codierungen (binär–…“) |
Höfler (Diskussion | Beiträge) K (Textersetzung - „Biografien_und_Bibliografien/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29“ durch „Biografien_und_Bibliografien/An_LNTwww_beteiligte_LÜT-Angehörige#Dr.-Ing._Tasn.C3.A1d_Kernetzky_.28bei_L.C3.9CT_von_2014-2022.29“) |
||
| (38 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|gram-schmidt}} |
| + | |||
==Programmbeschreibung== | ==Programmbeschreibung== | ||
<br> | <br> | ||
| − | Das Applet verdeutlicht | + | Das Applet verdeutlicht das »Gram–Schmidt–Verfahren«. Dieses ermöglicht, eine Menge $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ energiebegrenzter Signale mit Hilfe von $N \le M$ orthonormalen Basisfunktionen $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$ in folgender Form darzustellen: |
| − | |||
| − | |||
| + | :$$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , | ||
| + | \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | Der vektorielle Repräsentant der Musterfunktion $s_1(t)$ lautet dann: | |
| + | :$$\mathbf{s}_i = \big( s_{i1}\hspace{0.05cm}, \hspace{0.3cm}s_{i2}\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm},\hspace{0.05cm} s_{iN} \big ).$$ | ||
| − | + | Das Applet zeigt alle Grafiken, die zum Verständnis des Gram–Schmidt–Verfahrens erforderlich sind, und als jeweiliges Ergebnis | |
| + | * die 2D–Darstellung der $M$ vektoriellen Repräsentanten, falls $N=2$, | ||
| − | + | * die 3D–Darstellung der $M$ vektoriellen Repräsentanten, falls $N=3$. | |
| − | + | ==English Description== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
| − | + | This applet illustrates the »Gram–Schmidt process«. This allows to represent a set $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ of energy-limited signals in the following form, using $N \le M$ orthonormal basis functions $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$: | |
| − | + | :$$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , | |
| − | + | \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N | |
| − | + | \hspace{0.05cm}.$$ | |
| − | + | The vectorial representative of the pattern function $s_1(t)$ is then: | |
| − | + | :$$\mathbf{s}_i = \big( s_{i1}\hspace{0.05cm}, \hspace{0.3cm}s_{i2}\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm},\hspace{0.05cm} s_{iN} \big ).$$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | + | The applet shows all the graphics, necessary to understand the Gram–Schmidt process, and as the respective result. |
| + | * the two-dimensional representation of the $M$ vectorial representatives, if $N=2$, | ||
| + | * the three-dimensional representation of the $M$ vectorial representatives, if $N=3$. | ||
| − | |||
| − | + | ==Theoretischer Hintergrund== | |
| − | + | === Signaldarstellung mit orthonormalen Basisfunktionen === | |
| − | + | Wir gehen von einer Menge $\{s_i(t)\}$ möglicher Sendesignale aus, die den möglichen Nachrichten $m_i$ eineindeutig zugeordnet sind. Mit $i = 1$, ... , $M$ gelte: | |
| − | + | :$$m \in \{m_i \}, \hspace{0.2cm} s(t) \in \{s_i(t) \}\hspace{-0.1cm}: \hspace{0.3cm} m = m_i \hspace{0.1cm} \Leftrightarrow \hspace{0.1cm} s(t) = s_i(t) \hspace{0.05cm}.$$ | |
| − | :$$\ | ||
| − | |||
| − | |||
| − | + | Für das Folgende setzen wir weiter voraus, dass die $M$ Signale $s_i(t)$ [[Signaldarstellung/Klassifizierung_von_Signalen#Energiebegrenzte_und_leistungsbegrenzte_Signale| energiebegrenzt]] sind, was meist gleichzeitig bedeutet, dass sie nur von endlicher Dauer sind. | |
| − | |||
| − | |||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Satz:}$ Eine jede Menge $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ energiebegrenzter Signale lässt sich in $N \le M$ '''orthonormale Basisfunktionen''' $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$ entwickeln. Es gilt: | ||
| − | $ | + | :$$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , |
| − | + | \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N | |
| − | + | \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Jeweils zwei Basisfunktionen $\varphi_j(t)$ und $\varphi_k(t)$ müssen orthonormal zueinander sein, das heißt, dass gelten muss $(\delta_{jk}$ nennt man das [https://de.wikipedia.org/wiki/Kronecker-Delta Kronecker–Symbol]$)$: | ||
| − | + | :$$<\hspace{-0.1cm}\varphi_j(t), \hspace{0.05cm}\varphi_k(t) \hspace{-0.1cm}> = \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\,d \it t = {\rm \delta}_{jk} = | |
| − | + | \left\{ \begin{array}{c} 1 \\ | |
| + | 0 \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {\rm falls}\hspace{0.4cm}j = k\hspace{0.1cm} | ||
| + | \\ {\rm falls}\hspace{0.4cm} j \ne k \hspace{0.1cm}\\ \end{array} | ||
| + | \hspace{0.05cm}.$$}}<br> | ||
| − | :$$ | + | Der Parameter $N$ gibt dabei an, wieviele Basisfunktionen $\varphi_j(t)$ benötigt werden, um die $M$ möglichen Sendesignale darzustellen. Mit anderen Worten: $N$ ist die »Dimension des Vektorraums«, der von den $M$ Signalen aufgespannt wird. Dabei gilt: |
| + | *Ist $N = M$, so sind alle Sendesignale zueinander orthogonal. Sie sind nicht notwendigerweise orthonormal, das heißt, die Energien $E_i = \ <\hspace{-0.01cm}s_i(t), \hspace{0.05cm}s_i(t) \hspace{-0.01cm}>$ können durchaus ungleich Eins sein.<br> | ||
| − | + | *Der Fall $N < M$ ergibt sich, wenn mindestens ein Signal $s_i(t)$ als Linearkombination von Basisfunktionen $\varphi_j(t)$ dargestellt werden kann, die sich bereits aus anderen Signalen $s_j(t) \ne s_i(t)$ ergeben haben.<br> | |
| − | |||
| − | |||
| − | |||
| + | [[Datei:P ID1993 Dig T 4 1 S2 version1.png|right|frame|Darstellung der drei Sendesignale durch zwei Basisfunktionen|class=fit]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Wir betrachten $M = 3$ energiebegrenzte Signale gemäß der Grafik. | ||
| − | + | Man erkennt sofort: | |
| − | + | *Die Signale $s_1(t)$ und $s_2(t)$ sind zueinander orthogonal.<br> | |
| − | Man erkennt | ||
| − | * | ||
| − | |||
| − | |||
| − | |||
| + | *Die Energien sind $E_1 = A^2 \cdot T = E$ und $E_2 = (A/2)^2 \cdot T = E/4$.<br> | ||
| − | $\ | + | *Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sind jeweils formgleich mit $s_1(t)$ bzw. $s_2(t)$. |
| − | + | *Beide Signale besitzen jeweils die Energie „Eins”: | |
| + | :$$\varphi_1(t)=\frac{s_1(t)}{\sqrt{E_1} } = \frac{s_1(t)}{\sqrt{A^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_1(t)}{A}$$ | ||
| + | :$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_1(t) = s_{11} \cdot \varphi_1(t)\hspace{0.05cm},\hspace{0.1cm}s_{11} = \sqrt{E}\hspace{0.05cm},$$ | ||
| + | :$$\varphi_2(t) =\frac{s_2(t)}{\sqrt{E_2} } = \frac{s_2(t)}{\sqrt{(A/2)^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_2(t)}{A/2}\hspace{0.05cm}$$ | ||
| + | :$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_2(t) = s_{21} \cdot \varphi_2(t)\hspace{0.05cm},\hspace{0.1cm}s_{21} = {\sqrt{E} }/{2}\hspace{0.05cm}.$$ | ||
| − | === | + | *Das Signal $s_3(t)$ kann durch die vorher bestimmten Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ ausgedrückt werden: |
| + | :$$s_3(t) =s_{31} \cdot \varphi_1(t) + s_{32} \cdot \varphi_2(t)\hspace{0.05cm},$$ | ||
| + | :$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm} | ||
| + | s_{31} = {A}/{2} \cdot \sqrt {T}= {\sqrt{E} }/{2}\hspace{0.05cm}, \hspace{0.2cm}s_{32} = - A \cdot \sqrt {T} = -\sqrt{E} \hspace{0.05cm}.$$ | ||
| − | + | Trotz $M=3$ gilt also im vorliegenen Fall nur $N=2$. | |
| − | + | Im rechten unteren Bild sind die Signale in einer 2D–Darstellung mit den Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ als Achsen dargestellt, wobei $E = A^2 \cdot T$ gilt und der Zusammenhang zu den anderen Grafiken durch die Farbgebung zu erkennen ist. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Die vektoriellen Repräsentanten der Signale $s_1(t)$, $s_2(t)$ und $s_3(t)$ in diesem zweidimensionellen Vektorraum lassen sich daraus wie folgt ablesen: | |
| + | :$$\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), \hspace{0.5cm} | ||
| + | \mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), \hspace{0.5cm} \mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.$$}} | ||
| + | <br clear= all> | ||
| − | + | === Das Verfahren nach Gram-Schmidt=== | |
| − | |||
| − | |||
| − | |||
| − | + | Im letzten $\text{Beispiel}$ war die Bestimmung der beiden orthonormalen Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sehr einfach, da diese formgleich mit $s_1(t)$ bzw. $s_2(t)$ waren. Das [https://de.wikipedia.org/wiki/Gram-Schmidtsches_Orthogonalisierungsverfahren Gram–Schmidt–Verfahren] findet die Basisfunktionen $\varphi_1(t)$, ... , $\varphi_N(t)$ für beliebig vorgebbare Signale $s_1(t)$, ... , $s_M(t)$, und zwar wie folgt: | |
| − | :$$ | + | *Die erste Basisfunktion $\varphi_1(t)$ ist stets formgleich mit $s_1(t)$. Es gilt: |
| − | \ | + | :$$\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} |
| − | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm \ddot{u}r }}\hspace{0.2cm} j \ge 2 | |
| − | )\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Hinweise zur Nomenklatur:}$ | |
| − | |||
| − | |||
| + | '''(1)''' Ausgehend von zwei reellen und energiebegrenzten Zeitfunktionen $x(t)$ und $y(t)$ erhält man für das [https://de.wikipedia.org/wiki/Inneres_Produkt innere Produkt] allgemein: | ||
| + | :$$<\hspace{-0.01cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.01cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | '''(2)''' Daraus ergibt sich die [https://de.wikipedia.org/wiki/Euklidische_Norm Euklidische Norm] der Zeitfunktion $s_1(t)$: | |
| − | + | :$$\vert \vert s_1(t) \vert \vert = \sqrt{<\hspace{-0.01cm}s_1(t), \hspace{0.15cm}s_1(t) \hspace{-0.01cm}>} $$}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Es wird nun angenommen, dass aus den Signalen $s_1(t)$, ... , $s_{k-1}(t)$ bereits die Basisfunktionen $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ berechnet wurden $(n \le k)$. | ||
| − | + | *Dann berechnen wir mittels der nächsten Funktion $s_k(t)$ die Hilfsfunktion | |
| − | * | + | :$$\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm mit}\hspace{0.4cm} |
| − | + | s_{kj} = \hspace{0.01cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.01cm} >, \hspace{0.2cm} j = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm}, n-1\hspace{0.05cm}.$$ | |
| − | |||
| + | *Hat diese Hilfsfunktion die Norm $||\theta_k(t)|| = 0$, so liefert $s_k(t)$ keine neue Basisfunktion. Vielmehr lässt sich dann $s_k(t)$ durch die $n-1$ bereits vorher gefundenen Basisfunktionen $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ ausdrücken: | ||
| + | :$$s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.$$ | ||
| − | + | *Eine neue Basisfunktion (nämlich die $n$–te) ergibt sich nur für den Fall $||\theta_k(t)|| \ne 0$: | |
| − | + | :$$\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} | |
| − | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.$$ | |
| − | |||
| − | + | Diese Prozedur wird solange fortgesetzt, bis alle $M$ Signale berücksichtigt wurden. | |
| + | *Danach hat man alle $N \le M$ orthonormalen Basisfunktionen $\varphi_j(t)$ gefunden. | ||
| + | |||
| + | *Der Sonderfall $N = M$ ergibt sich nur dann, wenn alle $M$ Signale linear voneinander unabhängig sind.<br> | ||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel 2:}$ Wir betrachten die $M = 4$ energiebegrenzten Signale $s_1(t)$, ... , $s_4(t)$ entsprechend der Grafik. Zur Vereinfachung der Berechnungen sind hier sowohl die Amplituden als auch die Zeit normiert. | |
| − | + | [[Datei:Dig_T_4_1_S3_neu.png|center|frame|Zum Gram-Schmidt-Verfahren|class=fit]] | |
| − | |||
| − | + | Man erkennt aus diesen Skizzen: | |
| + | *Die Basisfunktion $\varphi_1(t)$ ist formgleich mit $s_1(t)$. Wegen $E_1 = \vert \vert s_1(t) \vert \vert ^2 = 3 \cdot 0.5^2 = 0.75$ ergibt sich $s_{11} = \vert \vert s_1(t) \vert \vert = 0.866$. $\varphi_1(t)$ selbst besitzt abschnittsweise die Werte $\pm 0.5/0.866 = \pm0.577$. | ||
| + | *Zur Berechnung der Hilfsfunktion $\theta_2(t)$ berechnen wir | ||
| − | + | :$$s_{21} = \hspace{0.1cm} < \hspace{-0.01cm} s_2(t), \hspace{0.05cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.01cm} = 0 \cdot (+0.577) + 1 \cdot (-0.577)+ 0 \cdot (-0.577)= -0.577$$ | |
| − | $\Rightarrow \ \ | + | :$$ \Rightarrow \hspace{0.3cm}\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = (0.333, \hspace{0.15cm} 0.667, \hspace{0.15cm} -0.333) |
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\vert \vert \theta_2(t) \vert \vert^2 = (1/3)^2 + (2/3)^2 + (-1/3)^2 = 0.667$$ | ||
| + | :$$ \Rightarrow \hspace{0.3cm} s_{22} = \sqrt{0.667} = 0.816,\hspace{0.3cm} | ||
| + | \varphi_2(t) = \theta_2(t)/s_{22} = (0.408, \hspace{0.15cm} 0.816, \hspace{0.15cm} -0.408)\hspace{0.05cm}. $$ | ||
| − | Die | + | *Die inneren Produkte zwischen $s_1(t)$ mit $\varphi_1(t)$ bzw. $\varphi_2(t)$ liefern folgende Ergebnisse: |
| − | + | :$$s_{31} \hspace{0.01cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_1(t) \hspace{-0.01cm} > \hspace{0.1cm} = 0.5 \cdot (+0.577) + 0.5 \cdot (-0.577)- 0.5 \cdot (-0.577)= 0.289,$$ | |
| − | + | :$$s_{32} \hspace{0.1cm} = \hspace{0.01cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_2(t) \hspace{-0.01cm} > \hspace{0.1cm} = 0.5 \cdot (+0.408) + 0.5 \cdot (+0.816)- 0.5 \cdot (-0.408)= 0.816$$ | |
| + | :$$\Rightarrow \hspace{0.3cm}\theta_3(t) = s_3(t) - 0.289 \cdot \varphi_1(t)- 0.816 \cdot \varphi_2(t) = 0\hspace{0.05cm}.$$ | ||
| + | Das bedeutet: Die grüne Funktion $s_3(t)$ liefert keine neue Basisfunktion $\varphi_3(t)$, im Gegensatz zur Funktion $s_4(t)$. Die numerischen Ergebnisse hierfür können der Grafik entnommen werden.}} | ||
| − | |||
| − | |||
| − | |||
| − | + | ===Die verschiedenen Rubriken bei der Auswahl der Programmparameter=== | |
| − | + | Das Programm bietet insgesamt $4 \cdot 6 = 24$ Möglichkeiten zur Einstellung der jeweiligen Menge $\{s_i(t)\}$ möglicher Sendesignale. Diese $24$ Parametersätze sind in vier Rubriken eingeteilt. Die vier Rubriküberschriften treffen den Sachverhalt nicht hundertprozentig und sind deshalb in Hochkommata gesetzt: | |
| − | |||
| + | '''(1)''' Rubrik »$\text{Basisband}$«</u> ⇒ gültig für die Einstellungen $\rm (A)$ ... $\rm (F)$: | ||
| + | [[Datei:Gram_1_version2.png|right|frame|Signalform bei „Basisband”]] | ||
| + | *Jedes Mustersignal $s_i(t)$ besteht aus drei Rechteckfunktionen unterschiedlicher Höhen und jeweiliger Dauer $T$. | ||
| + | *Die einzelnen Rechteckhöhen sind Vielfache von $\pm 0.25$ und die gesamte Signaldauer ergibt $3T$. | ||
| + | *Mit dem seitlichen Slider kann man das Signal $s_i(t)$ um Vielfache von $\pm 0.25$ nach oben und unten verschieben. | ||
| + | *Solche Signale treten zum Beispiel bei der binären oder mehrstufigen [[Digitalsignalübertragung/Redundanzfreie_Codierung#Quatern.C3.A4rsignal_mit_rc_.3D_0_und_Tern.C3.A4rsignal_mit_rc_.E2.89.88_0|Basisbandübertragung]] auf. | ||
| + | *Im Beispiel 2 des hier angegebenen Links erkennt man zum Beispiel die grafischen Darstellungen | ||
| + | :* eines binären Signals $q(t)$, | ||
| + | :* eines ternären Signals $s_3(t)$, | ||
| + | :* eines quaternären Signals $s_4(t)$. | ||
| + | <br clear=all> | ||
| + | '''(2)''' Rubrik »$\text{M-ASK/BPSK}$«</u> ⇒ gültig für die Einstellungen $\rm (G)$ ... $\rm (L)$: | ||
| + | [[Datei:Gram_2_version2.png|right|frame|Signalform bei „''M''–ASK / BPSK”]] | ||
| + | *Die Mustersignale $s_i(t)$ haben ebenfalls die Dauer $3T$ und sind ähnlich aufgebaut wie bei der Rubrik '''(1)'''. | ||
| + | * Im Unterschied zu '''(1)''' wird jede Rechteckfunktion $($Dauer $T)$ durch eine Periode einer Sinusfunktionen ersetzt. | ||
| + | *Der angegebene Zahlenwert gibt hier die Amplitude des sinusförmigen Teilstücks an. | ||
| + | *Bei negativem Vorzeichen wird aus dem „Sinus” die Funktion „Minus–Sinus”. | ||
| + | *Mit dem seitlichen Slider kann man die Amplitude von $s_i(t)$ um Vielfache von $\pm 0.25$ vergrößern oder verkleinern. | ||
| + | *Solche Signale können zum Beispiel bei der [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#M.E2.80.93stufiges_Amplitude_Shift_Keying_.28M.E2.80.93ASK.29|''M''–ASK]] $($mehrstufiges "Amplitude Shift Keying"$)$ auftreten, ebenso bei [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#Binary_Phase_Shift_Keying_.28BPSK.29|BPSK]] $($"Binary Phase Shift Keying"$)$. | ||
| + | <br clear=all> | ||
| + | '''(3)''' Rubrik »$\text{Nur eine Frequenz}$«</u> ⇒ gültig für die Einstellungen $\rm (M)$ ... $\rm (R)$: | ||
| + | [[Datei:Gram_3_version4.png|right|frame|Signalform bei „Nur eine Frequenz”]] | ||
| + | *Alle Mustersignale $s_i(t)$ haben die Dauer $T$ und sind jeweils Harmonische Schwingungen der Form | ||
| + | :$$s_i(t) = A_i \cdot \cos(2\pi \cdot f_k \cdot t + \phi_i)\hspace{0.3cm}\text{mit}\hspace{0.3cm}f_k=K/T.$$ | ||
| + | *Die Eigenschaft „Nur eine Frequenz” bezieht sich auf die einzelnen Mustersignale $s_i(t)$ und auf den gesamten Set. | ||
| + | *Der Parameter $K$ gibt die Anzahl der Schwingungen innerhalb der Zeit $T$ an und gilt für alle Mustersignale. | ||
| + | *Die Grafik gilt für: $A_i=0.75, \hspace{0.3cm}f_k= 4/T \hspace{0.3cm}\Rightarrow\hspace{0.3cm}K=4, \hspace{0.3cm}\phi_i=- 90^\circ$ ⇒ '''sinusförmiger Verlauf'''. | ||
| − | + | *Mit dem Slider lässt sich die Phase von $s_i(t)$ um Vielfache von $\pm 22.5^\circ$ in beide Richtungen variieren. | |
| − | + | *Solche Harmonische haben für alle (analogen und digitalen) Nachrichtensysteme große Bedeutung. | |
| − | + | <br clear=all> | |
| − | + | '''(4)''' Rubrik »$\text{Mehrere Frequenzen}$«</u> ⇒ gültig für die Einstellungen $\rm (S)$ ... $\rm (X)$: | |
| − | + | *Es gelten ähnliche Voraussetzungen wie für die „Rubrik 3”, es sind aber nun stets mehrere Frequenzen beteiligt. | |
| − | + | *Die Eigenschaft „Mehrere Frequenzen” bezieht sich auf einzelne Mustersignale $s_i(t)$ oder auch auf den gesamten Set $\{s_i(t)\}$. | |
| − | + | *Möglich sind somit auch Mustersignale der folgenden Form $($mit $k=0$ ⇒ $f=f_0 = k/T = 0$ ⇒ Gleichsignal$)$: | |
| − | + | :$$s_i(t) = 1 \cdot \cos(2\pi \cdot f_0 \cdot t) - 0.5 \cdot \cos(2\pi \cdot f_2 \cdot t)-0.5 \cdot \cos(2\pi \cdot f_3 \cdot t).$$ | |
| − | + | *Der Parameter $k$ muss auch nicht ganzzahlig sein. Beispielsweise kennzeichnet $k= 4.5$ viereinhalb Schwingunen Schwingungen innerhalb der Zeitdauer $T$. | |
| − | $ | + | *Mit dem Slider können die Frequenzkenngrößen $k$ um Vielfache von $0.25$ vergrößert oder verkleinert werden. |
| − | + | <br clear=all> | |
| − | |||
| − | * | ||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | *$ | ||
| − | |||
| − | |||
| + | <br clear=all> | ||
==Versuchsdurchführung== | ==Versuchsdurchführung== | ||
<br> | <br> | ||
| − | [[Datei: | + | [[Datei:Gram_13_verion1.png|right|500px]] |
*Wählen Sie zunächst die Nummer ('''1''', ...) der zu bearbeitenden Aufgabe. | *Wählen Sie zunächst die Nummer ('''1''', ...) der zu bearbeitenden Aufgabe. | ||
| Zeile 232: | Zeile 222: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' | + | '''(1)''' Es gilt die Einstellung $\rm A$. Interpretieren Sie die ausgegebenen Grafiken. Wählen Sie hierfür „Einzelschritt”. }} |
| − | ::* | + | ::* Einstellung $\rm A$ beschreibt das $\text{Beispiel 2}$ im Theorieteil. Die Basisfunktion $\varphi_1(t)$ ist identisch mit dem Signal $s_1(t)$, aber mit Signalenergie $E=1$. |
| − | + | ::* Es gibt hier nur $N=3$ Basisfunktionen, da die Hilfsfunktion $\theta_3(t)$ identisch Null ist. | |
| − | + | ::* Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ können im 3D–Vektorraum abgelesen werden; Beispiel: $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' | + | '''(2)''' Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm B$. Wählen Sie hierfür und bei den weiteren Aufgaben „Gesamtdarstellung”. }} |
| − | ::* | + | ::* Auch hier gibt es $N=3$ Basisfunktionen. Bei Änderung auf $s_4 = (-1, \hspace{0.15cm} -1, \hspace{0.25cm} 0)$ nur mehr $N=2$. |
| − | |||
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(3)''' | + | '''(3)''' Bei der Einstellung $\rm C$ ist die Reihenfolge der Signale gegenüber $\rm B$ vertauscht. Wie wirkt sich das auf die Basisfunktionen aus?}} |
| − | ::* | + | ::* Auch hier gibt es $N=3$ Basisfunktionen, aber nun andere: Nämlich $\varphi_1(t) = s_1(t)$, $\varphi_2(t) = s_2(t)$, $\varphi_3(t) = s_3(t)$. |
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(4)''' | + | '''(4)''' Die $M=4$ Signale der Einstellung $\rm D$ lassen sich durch nur $N=2$ Basisfunktionen ausdrücken? Begründen Sie dieses Ergebnis.}} |
| − | ::* | + | ::* Es gilt $s_3(t) = s_1(t)/4 - s_2(t)/2$ und $s_4(t) = -s_1(t) - s_2(t)$. Das heißt: $s_3(t)$ und $s_4(t)$ liefern keine neuen Basisfunktionen. |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(5)''' | + | '''(5)''' Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm E$ im Vergleich zur Einstellung $\rm D$.}} |
| − | ::* | + | ::* Bei der Einstellung $\rm E$ ist die Reihenfolge der Signale gegenüber der Einstellung $\rm D$ vertauscht. Ähnlich wie zwischen $\rm B$ und $\rm C$. |
| − | + | ::* Auch diese $M=4$ Signale lassen sich somit durch nur $N=2$ Basisfunktionen ausdrücken, aber durch andere als in der Aufgabe '''(4)'''. | |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(6)''' | + | '''(6)''' Welches Ergebnis liefern die vier Signale gemäß der Einstellung $\rm F$?}} |
| − | ::* | + | ::* Die die Signale $s_1(t)$, ... , $s_4(t)$ basieren alle auf einer einzigen Basisfunktion $\varphi_1(t)$, die formgleich mit $s_1(t)$ ist. Es gilt $N=1$. |
| − | ::* | + | ::* Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ sind $\pm 0.866$ und $\pm 1.732$. Sie liegen inder 2D–Darstellung alle auf einer Linie. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(7)''' | + | '''(7)''' Es gilt nun die „''M''–ASK / BPSK”–Einstellung $\rm G$. Interpretieren Sie das Ergebnis und versuchen Sie, einen Zusammenhang zu einer früheren Aufgabe herzustellen. }} |
| − | ::* | + | ::* Vergleicht man die angegebenen Zahlenwerte, so erkennt man, dass eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm A$. |
| − | ::* | + | ::* Der einzige Unterschied ist, dass nun alle Energien nur halb so groß sind wie vorher. Bezüglich der Amplituden wirkt sich das um den Faktor $\sqrt{2}$ aus. |
| − | ::* | + | ::* Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (-1.021, \hspace{0.15cm} -0.289, \hspace{0.15cm} +0.500)$ anstelle von $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$. |
| + | ::* Bei der Einstellung $\rm H$ sind gegenüber $\rm G$ alle Amplituden verdoppelt. Somit ergibt sich hier $\mathbf{s}_4 = (-2.041, \hspace{0.15cm} -0.577, \hspace{0.15cm} +1.000)$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(8)''' | + | '''(8)''' Es gelte die „''M''–ASK / BPSK”–Einstellung $\rm I$. Interpretieren Sie das Ergebnis. Versuchen Sie wieder, einen Zusammenhang zu einer früheren Aufgabe herzustellen.}} |
| − | ::* $ | + | ::* Hier wird eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm C$, aber nun mit nur halb so großen Energien. |
| − | ::* | + | ::* Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (+0.707, \hspace{0.15cm} -0.707, \hspace{0.15cm} 0.000)$ anstelle von $\mathbf{s}_4 = (+1.000, \hspace{0.15cm} -1.000, \hspace{0.15cm} 0.000)$. |
| − | + | ::* Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (+0.707, \hspace{0.15cm} -0.707, \hspace{0.15cm} 0.000)$ anstelle von $\mathbf{s}_4 = (+1.000, \hspace{0.15cm} -1.000, \hspace{0.15cm} 0.000)$. | |
| + | ::* Mit der „''M''–ASK / BPSK”–Einstellung $\rm J$ wird eine ähnliche Konstellation betrachtet wie mit der „Basisband”–Einstellung $\rm D$. Gleiches gilt für $\rm K$ und $\rm E$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(9)''' | + | '''(9)''' Es gelte die „''M''–ASK / BPSK”–Einstellung $\rm L$. Interpretieren Sie das Ergebnis. Gibt es einen Zusammenhang zu einer früheren Aufgabe?}} |
| + | ::* Die Einstellung $\rm L$ ist vergleichbar mit der obigen Einstellung $\rm F$. Es gilt $N=1$. Das heißt: | ||
| + | ::* Alle $M=4$ Signale sind allein durch die Basisfunktion $\varphi_1(t)$ darstellbar, die formgleich mit $s_1(t)$ ist. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | ::* | + | '''(10)''' Nun gelte die „Nur eine Frequenz”–Einstellung $\rm M$. Interpretieren Sie die dargestellten Grafiken. }} |
| + | |||
| + | ::* Alle Signale $s_i(t)$ haben die Amplitude $A_i = 1$ und gleiche Frequenz $f=f_1$. Das heißt: Jeweils eine Schwingung innerhalb der Zeit $T$. | ||
| + | ::* Die $M=4$ Signale unterscheiden sich nur durch die Phasen $\phi_1 = +45^\circ$, $\phi_2 = +135^\circ$, $\phi_3 = -135^\circ$ und $\phi_4 = -45^\circ$. Es gibt $N=2$ Basisfunktionen. | ||
| + | ::* Die Basisfunktion $\varphi_1(t)$ ist formgleich mit $s_1(t)$ und $\varphi_2(t)$ ist formgleich mit $s_2(t)$. Dies gilt für die meisten Einstellungen der dritten Rubrik. | ||
| + | ::*Die vektoriellen Repräsentanten der Signale lauten: $\mathbf{s}_1 = (0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_2 = (0, \hspace{0.15cm} 0.707)$, $\mathbf{s}_3 = (-0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_4 = (0, \hspace{0.15cm} -0.707)$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(11)''' Welche Unterschiede gibt es mit der Einstellung $\rm N$ gegenüber der Einstellung $\rm M$? }} |
| + | |||
| + | ::* Die vier Mustersignale $s_i(t)$ beschreiben nun von oben nach unten einen Cosinus, einen Sinus, einen Minus–Cosinus und einen Minus–Sinus. | ||
| + | ::* Für die $N=2$ Basisfunktionen gilt: $\varphi_1(t) = \sqrt{2} \cdot \cos(2\pi f_1 t)$, $\varphi_2(t) = \sqrt{2} \cdot\sin(2\pi f_1 t)$. Auch $s_3(t)$ und $s_4(t)$ lassen sich damit beschreiben. | ||
| + | ::* Die vektoriellen Repräsentanten der Signale lauten: $\mathbf{s}_1 = (0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_2 = (0, \hspace{0.15cm} 0.707)$, $\mathbf{s}_3 = (-0.354, \hspace{0.15cm} 0)$, $\mathbf{s}_4 = (0, \hspace{0.15cm} -0.354)$. | ||
| + | ::* Dieses Ergebnis berücksichtigt die nur halb so großen Amplituden von $s_3(t)$ und $s_4(t)$ gegenüber $s_1(t)$ und $s_2(t)$. | ||
| − | ::* | + | {{BlaueBox|TEXT= |
| − | ::* | + | '''(12)''' Wie unterscheidet sich die Einstellung $\rm O$ von der Einstellung $\rm N$? Analysieren Sie den vektoriellen Repräsentanten für $\mathbf{s}_3$ genauer.}} |
| + | ::* Das Signal $s_2(t)$ bei Einstellung $\rm O$ ist minus–sinusförmig ⇒ $\varphi_1(t) = \sqrt{2} \cdot \cos(2\pi f_1 t)$, $\varphi_2(t) = -\sqrt{2} \cdot\sin(2\pi f_1 t)$. | ||
| + | ::* Für die Darstellung Harmonischer Schwingungen werden häufig diese Basisfunktionen „Cosinus” und „Minus–Sinus” verwendet. | ||
| + | ::* Außerdem unterscheiden sich die Signale $s_3(t)$ und $s_4(t)$ durch die halbe Amplitude und die Phsenwerte sind keine Vielfachen von $90^\circ$. | ||
| + | ::*Die vektoriellen Repräsentanten der Signale lauten: $\mathbf{s}_1 = (0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_2 = (0, \hspace{0.15cm} 0.707)$, $\mathbf{s}_3 = (0.612, \hspace{0.15cm} 0.354)$, $\mathbf{s}_4 = (0.354, \hspace{0.15cm} -0.612)$. Überprüfung: | ||
| + | ::*$s_3(t) = \cos(2\pi f_1 t + 30^\circ) = \cos(30^\circ) \cdot \cos(2\pi f_1 t)\hspace{-0.05cm} - \hspace{-0.05cm} \sin(30^\circ) \cdot \sin(2\pi f_1 t)=\sqrt{3}/(2\sqrt{2})\cdot \varphi_1(t) + 1/(2\sqrt{2})\cdot \varphi_2(t)= 0.612\cdot \varphi_1(t) + 0.354\cdot \varphi_2(t)$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(13)''' Wie unterscheidet sich die Einstellung $\rm P$ von der Einstellung $\rm O$? Gibt es in der Rubrik „Nur eine Frequenz” eine Einstellung für $N=1$ ?}} |
| − | ::* $ | + | ::*Mit der Einstellung $\rm P$ ergeben sich gleiche vektorielle Repräsentanten. Einziger Unterschied zur Einstellung $\rm O$ ist die doppelte Frequenz. |
| − | ::* | + | ::*Das Ergebnis $N=1$ ist nur möglich, wenn alle Signale gleiche Frequenz und gleiche Phase besitzen ⇒ Einstellung $\rm R$ $($unterschiedliche Amplituden$)$. |
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(14)''' Nun gelte die „Mehrere Frequenzen”–Einstellung $\rm S$. Interpretieren Sie die dargestellten Grafiken. }} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ::*Die vier Signale $s_1(t)$ ... $s_4(t)$ weisen nun unterschiedliche Frequenzen auf: $f=0$ (Gleichsignal), $f=f_1$, $f=f_2 = 2f_1$, $f=f_3 = 3f_1$. | |
| − | + | ::*Deshalb ergeben sich hier $N=4$ Basisfunktionen $\varphi_i(t)$, die alle formgleich mit den entsprechenden Signalen $s_i(t)$ sind. Für $i=1$ gilt: $\varphi_1(t)=1$. | |
| − | + | ::*Die weiteren Basisfunktionen haben wegen der Energienormierung einheitlich die Form $\varphi_i(t)= \sqrt{2}\cdot \cos(2\pi f_i t)$. | |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(15)''' Wie unterscheidet sich die Einstellung $\rm T$ von der Einstellung $\rm S$? Begründen Sie das Ergebnis $N=3$. Interpretieren Sie auch die Grafiken zur Einstellung $\rm U$.}} |
| − | |||
| − | |||
| − | |||
| − | == | + | ::*Die Signale $s_1(t)$ ... $s_3(t)$ beinhalten die Frequenzen $f=0$, $f=f_1$ und $f=f_2 = 2f_1$. Jedes Signal erzwingt eine eigene Basisfunktion. |
| − | + | ::*Die vektoriellen Repräsentanten dieser Signale lauten: $\mathbf{s}_1 = (1, \hspace{0.15cm} 0, \hspace{0.15cm} 0)$, $\mathbf{s}_2 = (0, \hspace{0.15cm} 0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_3 = (0, \hspace{0.15cm} 0,\hspace{0.15cm} 0.707)$. | |
| − | + | ::*Das vierte Signal ist als Linearkombination darstellbar: $s_4(t)=s_1(t)-0.5 \cdot s_2(t)-0.5 \cdot s_3(t)$ ⇒ vektorieller Repräsentant: $\mathbf{s}_1 = (1, \hspace{0.15cm} -0.354, \hspace{0.15cm} 0.354)$. | |
| − | | + | ::*Die Einstellung $\rm U$ ist nur eine zyklische Vertauschung von der Einstellung $\rm T$ ⇒ es genügen ebenfalls $N = 3$ Basisfunktionen. |
| + | ::*Die $N = 3$ Basisfunktionen sind aber deutlich komplizierter als bei $\rm T$, weil „Gram–Schmidt” signifikant von der Reihenfolge der Mustersignale abhängt. | ||
| − | + | {{BlaueBox|TEXT= | |
| + | '''(16)''' Interpretieren Sie die dargestellten Grafiken für die Einstellung $\rm V$ und anschließend für die Einstellung $\rm W$. }} | ||
| + | ::*Die ersten drei Signale führen zu je einer cosinusförmigen Basisfunktion mit den Frequenzen $f_2$, $f_3$ und $f_4$. | ||
| + | ::*Das letzte Signal ist $s_4(t)= \cos(2\pi f_3 t) \cdot \cos(2\pi f_1 t) = 1/2 \cdot\big [ \cos(2\pi \cdot (f_3 - f_1)\cdot t) + \cos(2\pi \cdot (f_3 + f_1)\cdot t)\big ] = 1/2 \cdot \big [\cos(2\pi f_2 t) + \cos(2\pi f_4 t)\big ] $. | ||
| + | ::* Der vektorielle Repräsentant des untersten Signals gemäß Einstellung $\rm V$ lautet somit: $\mathbf{s}_4 = (0.354, \hspace{0.15cm} 0, \hspace{0.15cm} 0.354)$. | ||
| + | ::* Bei der Einstellung $\rm W$ ergeben sich genau die gleichen Basisfunktionen wie bei $\rm W$. Hier erhält man für das unterste Signal $\mathbf{s}_4 = (0.354, \hspace{0.15cm} 0, \hspace{0.15cm} -0.354)$. | ||
| + | ::*Begründung $s_4(t)= \sin(2\pi f_3 t) \cdot \sin(2\pi f_1 t) = 1/2 \cdot \big [\cos(2\pi f_2 t) - \cos(2\pi f_4 t)\big ] $. Auch hier liefert die Basisfunktion $\varphi_2(t)$ keinen Beitrag. | ||
| − | + | {{BlaueBox|TEXT= | |
| + | '''(17)''' Wie viele Basisfunktionen benötigt man für die vier Signale gemäß der Einstellung $\rm X$? }} | ||
| + | ::*Das Ergebnis lautet: $N = 4$. Jedes der vier Signale $\cos(2\pi f_1 t)$, $\sin(2\pi f_1 t)$ $\cos(2\pi f_2 t)$, $\sin(2\pi f_2 t)$ führt zu einer neuen Basisfunktion. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | '''( | + | ==Zur Handhabung des Applets== |
| + | <br> | ||
| + | [[Datei:Gram_11_version2.png|left|600px|frame|Bildschirmabzug]] | ||
| + | '''(A)''' Auswahl zwischen 24 Parametersätze für $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ | ||
| − | '''( | + | '''(B)''' Umschaltung: Einzelschritt / Gesamtdarstellung |
| − | '''( | + | '''(C)''' 2D– bzw. 3D–Darstellung der vektoriellen Repräsentanten<br> |
| + | (siehe rechte Grafik, Koordinatensystem kann gedreht werden) | ||
| − | '''( | + | '''(D)''' Reset – Rücksetzung aller Parameter auf Grundeinstellung |
| − | '''( | + | '''(E)''' Grafikfeld zur Darstellung der Mustersignale $s_k(t)$ |
| − | '''( | + | '''(F)''' Grafikfeld zur Darstellung der Hilfsfunktionen $\theta_k(t)$ |
| − | '''( | + | '''(G)''' Grafikfeld zur Darstellung der Basisfunktionen $\varphi_k(t)$ |
| − | '''( | + | '''(H)''' Bereich für die Versuchsdurchführung: Aufgabenauswahl |
| − | + | [[Datei:Gram_12_verion1.png|right|300px|frame|3D–Darstellung der Repräsentanten]] | |
<br clear=all> | <br clear=all> | ||
==Über die Autoren== | ==Über die Autoren== | ||
| − | Dieses interaktive Berechnungstool wurde am [ | + | Dieses interaktive Berechnungstool wurde am [https://www.ce.cit.tum.de/lnt/startseite/ »Lehrstuhl für Nachrichtentechnik«] der [https://www.tum.de/ »Technischen Universität München«] konzipiert und realisiert. |
| − | *Die erste Version wurde 2008 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende# | + | *Die erste Version wurde 2008 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Martin_V.C3.B6lkl_.28Diplomarbeit_LB_2010.29|»Martin Völkl«]] im Rahmen seiner Diplomarbeit mit »FlashMX–Actionscript« erstellt $($Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|»Günter Söder«]]$)$. |
| − | * | + | |
| + | * 2020 wurde das Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|»Carolin Mirschina«]] im Rahmen einer Werkstudententätigkeit mit „HTML5” neu gestaltet $($Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_LÜT-Angehörige#Dr.-Ing._Tasn.C3.A1d_Kernetzky_.28bei_L.C3.9CT_von_2014-2022.29|»Tasnád Kernetzky«]]$)$. | ||
| − | Die Umsetzung dieses Applets auf HTML 5 wurde durch [https://www. | + | Die Umsetzung dieses Applets auf HTML 5 wurde durch das Programm [https://www.exzellenz.tum.de/startseite/ »EXIni«] (Exzellenzinitiative) der Technischen Universität München gefördert. Wir bedanken uns. |
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|gram-schmidt}} |
Aktuelle Version vom 26. Oktober 2023, 11:14 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Das Applet verdeutlicht das »Gram–Schmidt–Verfahren«. Dieses ermöglicht, eine Menge $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ energiebegrenzter Signale mit Hilfe von $N \le M$ orthonormalen Basisfunktionen $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$ in folgender Form darzustellen:
- $$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N \hspace{0.05cm}.$$
Der vektorielle Repräsentant der Musterfunktion $s_1(t)$ lautet dann:
- $$\mathbf{s}_i = \big( s_{i1}\hspace{0.05cm}, \hspace{0.3cm}s_{i2}\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm},\hspace{0.05cm} s_{iN} \big ).$$
Das Applet zeigt alle Grafiken, die zum Verständnis des Gram–Schmidt–Verfahrens erforderlich sind, und als jeweiliges Ergebnis
- die 2D–Darstellung der $M$ vektoriellen Repräsentanten, falls $N=2$,
- die 3D–Darstellung der $M$ vektoriellen Repräsentanten, falls $N=3$.
English Description
This applet illustrates the »Gram–Schmidt process«. This allows to represent a set $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ of energy-limited signals in the following form, using $N \le M$ orthonormal basis functions $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$:
- $$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N \hspace{0.05cm}.$$
The vectorial representative of the pattern function $s_1(t)$ is then:
- $$\mathbf{s}_i = \big( s_{i1}\hspace{0.05cm}, \hspace{0.3cm}s_{i2}\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm},\hspace{0.05cm} s_{iN} \big ).$$
The applet shows all the graphics, necessary to understand the Gram–Schmidt process, and as the respective result.
- the two-dimensional representation of the $M$ vectorial representatives, if $N=2$,
- the three-dimensional representation of the $M$ vectorial representatives, if $N=3$.
Theoretischer Hintergrund
Signaldarstellung mit orthonormalen Basisfunktionen
Wir gehen von einer Menge $\{s_i(t)\}$ möglicher Sendesignale aus, die den möglichen Nachrichten $m_i$ eineindeutig zugeordnet sind. Mit $i = 1$, ... , $M$ gelte:
- $$m \in \{m_i \}, \hspace{0.2cm} s(t) \in \{s_i(t) \}\hspace{-0.1cm}: \hspace{0.3cm} m = m_i \hspace{0.1cm} \Leftrightarrow \hspace{0.1cm} s(t) = s_i(t) \hspace{0.05cm}.$$
Für das Folgende setzen wir weiter voraus, dass die $M$ Signale $s_i(t)$ energiebegrenzt sind, was meist gleichzeitig bedeutet, dass sie nur von endlicher Dauer sind.
$\text{Satz:}$ Eine jede Menge $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ energiebegrenzter Signale lässt sich in $N \le M$ orthonormale Basisfunktionen $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$ entwickeln. Es gilt:
- $$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N \hspace{0.05cm}.$$
Jeweils zwei Basisfunktionen $\varphi_j(t)$ und $\varphi_k(t)$ müssen orthonormal zueinander sein, das heißt, dass gelten muss $(\delta_{jk}$ nennt man das Kronecker–Symbol$)$:
- $$<\hspace{-0.1cm}\varphi_j(t), \hspace{0.05cm}\varphi_k(t) \hspace{-0.1cm}> = \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\,d \it t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.4cm}j = k\hspace{0.1cm} \\ {\rm falls}\hspace{0.4cm} j \ne k \hspace{0.1cm}\\ \end{array} \hspace{0.05cm}.$$
Der Parameter $N$ gibt dabei an, wieviele Basisfunktionen $\varphi_j(t)$ benötigt werden, um die $M$ möglichen Sendesignale darzustellen. Mit anderen Worten: $N$ ist die »Dimension des Vektorraums«, der von den $M$ Signalen aufgespannt wird. Dabei gilt:
- Ist $N = M$, so sind alle Sendesignale zueinander orthogonal. Sie sind nicht notwendigerweise orthonormal, das heißt, die Energien $E_i = \ <\hspace{-0.01cm}s_i(t), \hspace{0.05cm}s_i(t) \hspace{-0.01cm}>$ können durchaus ungleich Eins sein.
- Der Fall $N < M$ ergibt sich, wenn mindestens ein Signal $s_i(t)$ als Linearkombination von Basisfunktionen $\varphi_j(t)$ dargestellt werden kann, die sich bereits aus anderen Signalen $s_j(t) \ne s_i(t)$ ergeben haben.
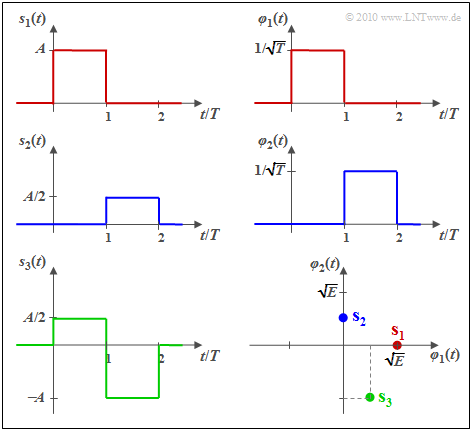
$\text{Beispiel 1:}$ Wir betrachten $M = 3$ energiebegrenzte Signale gemäß der Grafik.
Man erkennt sofort:
- Die Signale $s_1(t)$ und $s_2(t)$ sind zueinander orthogonal.
- Die Energien sind $E_1 = A^2 \cdot T = E$ und $E_2 = (A/2)^2 \cdot T = E/4$.
- Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sind jeweils formgleich mit $s_1(t)$ bzw. $s_2(t)$.
- Beide Signale besitzen jeweils die Energie „Eins”:
- $$\varphi_1(t)=\frac{s_1(t)}{\sqrt{E_1} } = \frac{s_1(t)}{\sqrt{A^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_1(t)}{A}$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_1(t) = s_{11} \cdot \varphi_1(t)\hspace{0.05cm},\hspace{0.1cm}s_{11} = \sqrt{E}\hspace{0.05cm},$$
- $$\varphi_2(t) =\frac{s_2(t)}{\sqrt{E_2} } = \frac{s_2(t)}{\sqrt{(A/2)^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_2(t)}{A/2}\hspace{0.05cm}$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_2(t) = s_{21} \cdot \varphi_2(t)\hspace{0.05cm},\hspace{0.1cm}s_{21} = {\sqrt{E} }/{2}\hspace{0.05cm}.$$
- Das Signal $s_3(t)$ kann durch die vorher bestimmten Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ ausgedrückt werden:
- $$s_3(t) =s_{31} \cdot \varphi_1(t) + s_{32} \cdot \varphi_2(t)\hspace{0.05cm},$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm} s_{31} = {A}/{2} \cdot \sqrt {T}= {\sqrt{E} }/{2}\hspace{0.05cm}, \hspace{0.2cm}s_{32} = - A \cdot \sqrt {T} = -\sqrt{E} \hspace{0.05cm}.$$
Trotz $M=3$ gilt also im vorliegenen Fall nur $N=2$.
Im rechten unteren Bild sind die Signale in einer 2D–Darstellung mit den Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ als Achsen dargestellt, wobei $E = A^2 \cdot T$ gilt und der Zusammenhang zu den anderen Grafiken durch die Farbgebung zu erkennen ist.
Die vektoriellen Repräsentanten der Signale $s_1(t)$, $s_2(t)$ und $s_3(t)$ in diesem zweidimensionellen Vektorraum lassen sich daraus wie folgt ablesen:
- $$\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), \hspace{0.5cm} \mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), \hspace{0.5cm} \mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.$$
Das Verfahren nach Gram-Schmidt
Im letzten $\text{Beispiel}$ war die Bestimmung der beiden orthonormalen Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sehr einfach, da diese formgleich mit $s_1(t)$ bzw. $s_2(t)$ waren. Das Gram–Schmidt–Verfahren findet die Basisfunktionen $\varphi_1(t)$, ... , $\varphi_N(t)$ für beliebig vorgebbare Signale $s_1(t)$, ... , $s_M(t)$, und zwar wie folgt:
- Die erste Basisfunktion $\varphi_1(t)$ ist stets formgleich mit $s_1(t)$. Es gilt:
- $$\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm \ddot{u}r }}\hspace{0.2cm} j \ge 2 \hspace{0.05cm}.$$
$\text{Hinweise zur Nomenklatur:}$
(1) Ausgehend von zwei reellen und energiebegrenzten Zeitfunktionen $x(t)$ und $y(t)$ erhält man für das innere Produkt allgemein:
- $$<\hspace{-0.01cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.01cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t \hspace{0.05cm}.$$
(2) Daraus ergibt sich die Euklidische Norm der Zeitfunktion $s_1(t)$:
- $$\vert \vert s_1(t) \vert \vert = \sqrt{<\hspace{-0.01cm}s_1(t), \hspace{0.15cm}s_1(t) \hspace{-0.01cm}>} $$
Es wird nun angenommen, dass aus den Signalen $s_1(t)$, ... , $s_{k-1}(t)$ bereits die Basisfunktionen $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ berechnet wurden $(n \le k)$.
- Dann berechnen wir mittels der nächsten Funktion $s_k(t)$ die Hilfsfunktion
- $$\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm mit}\hspace{0.4cm} s_{kj} = \hspace{0.01cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.01cm} >, \hspace{0.2cm} j = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm}, n-1\hspace{0.05cm}.$$
- Hat diese Hilfsfunktion die Norm $||\theta_k(t)|| = 0$, so liefert $s_k(t)$ keine neue Basisfunktion. Vielmehr lässt sich dann $s_k(t)$ durch die $n-1$ bereits vorher gefundenen Basisfunktionen $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ ausdrücken:
- $$s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.$$
- Eine neue Basisfunktion (nämlich die $n$–te) ergibt sich nur für den Fall $||\theta_k(t)|| \ne 0$:
- $$\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.$$
Diese Prozedur wird solange fortgesetzt, bis alle $M$ Signale berücksichtigt wurden.
- Danach hat man alle $N \le M$ orthonormalen Basisfunktionen $\varphi_j(t)$ gefunden.
- Der Sonderfall $N = M$ ergibt sich nur dann, wenn alle $M$ Signale linear voneinander unabhängig sind.
$\text{Beispiel 2:}$ Wir betrachten die $M = 4$ energiebegrenzten Signale $s_1(t)$, ... , $s_4(t)$ entsprechend der Grafik. Zur Vereinfachung der Berechnungen sind hier sowohl die Amplituden als auch die Zeit normiert.
Man erkennt aus diesen Skizzen:
- Die Basisfunktion $\varphi_1(t)$ ist formgleich mit $s_1(t)$. Wegen $E_1 = \vert \vert s_1(t) \vert \vert ^2 = 3 \cdot 0.5^2 = 0.75$ ergibt sich $s_{11} = \vert \vert s_1(t) \vert \vert = 0.866$. $\varphi_1(t)$ selbst besitzt abschnittsweise die Werte $\pm 0.5/0.866 = \pm0.577$.
- Zur Berechnung der Hilfsfunktion $\theta_2(t)$ berechnen wir
- $$s_{21} = \hspace{0.1cm} < \hspace{-0.01cm} s_2(t), \hspace{0.05cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.01cm} = 0 \cdot (+0.577) + 1 \cdot (-0.577)+ 0 \cdot (-0.577)= -0.577$$
- $$ \Rightarrow \hspace{0.3cm}\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = (0.333, \hspace{0.15cm} 0.667, \hspace{0.15cm} -0.333) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\vert \vert \theta_2(t) \vert \vert^2 = (1/3)^2 + (2/3)^2 + (-1/3)^2 = 0.667$$
- $$ \Rightarrow \hspace{0.3cm} s_{22} = \sqrt{0.667} = 0.816,\hspace{0.3cm} \varphi_2(t) = \theta_2(t)/s_{22} = (0.408, \hspace{0.15cm} 0.816, \hspace{0.15cm} -0.408)\hspace{0.05cm}. $$
- Die inneren Produkte zwischen $s_1(t)$ mit $\varphi_1(t)$ bzw. $\varphi_2(t)$ liefern folgende Ergebnisse:
- $$s_{31} \hspace{0.01cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_1(t) \hspace{-0.01cm} > \hspace{0.1cm} = 0.5 \cdot (+0.577) + 0.5 \cdot (-0.577)- 0.5 \cdot (-0.577)= 0.289,$$
- $$s_{32} \hspace{0.1cm} = \hspace{0.01cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_2(t) \hspace{-0.01cm} > \hspace{0.1cm} = 0.5 \cdot (+0.408) + 0.5 \cdot (+0.816)- 0.5 \cdot (-0.408)= 0.816$$
- $$\Rightarrow \hspace{0.3cm}\theta_3(t) = s_3(t) - 0.289 \cdot \varphi_1(t)- 0.816 \cdot \varphi_2(t) = 0\hspace{0.05cm}.$$
Das bedeutet: Die grüne Funktion $s_3(t)$ liefert keine neue Basisfunktion $\varphi_3(t)$, im Gegensatz zur Funktion $s_4(t)$. Die numerischen Ergebnisse hierfür können der Grafik entnommen werden.
Die verschiedenen Rubriken bei der Auswahl der Programmparameter
Das Programm bietet insgesamt $4 \cdot 6 = 24$ Möglichkeiten zur Einstellung der jeweiligen Menge $\{s_i(t)\}$ möglicher Sendesignale. Diese $24$ Parametersätze sind in vier Rubriken eingeteilt. Die vier Rubriküberschriften treffen den Sachverhalt nicht hundertprozentig und sind deshalb in Hochkommata gesetzt:
(1) Rubrik »$\text{Basisband}$« ⇒ gültig für die Einstellungen $\rm (A)$ ... $\rm (F)$:
- Jedes Mustersignal $s_i(t)$ besteht aus drei Rechteckfunktionen unterschiedlicher Höhen und jeweiliger Dauer $T$.
- Die einzelnen Rechteckhöhen sind Vielfache von $\pm 0.25$ und die gesamte Signaldauer ergibt $3T$.
- Mit dem seitlichen Slider kann man das Signal $s_i(t)$ um Vielfache von $\pm 0.25$ nach oben und unten verschieben.
- Solche Signale treten zum Beispiel bei der binären oder mehrstufigen Basisbandübertragung auf.
- Im Beispiel 2 des hier angegebenen Links erkennt man zum Beispiel die grafischen Darstellungen
- eines binären Signals $q(t)$,
- eines ternären Signals $s_3(t)$,
- eines quaternären Signals $s_4(t)$.
(2) Rubrik »$\text{M-ASK/BPSK}$« ⇒ gültig für die Einstellungen $\rm (G)$ ... $\rm (L)$:
- Die Mustersignale $s_i(t)$ haben ebenfalls die Dauer $3T$ und sind ähnlich aufgebaut wie bei der Rubrik (1).
- Im Unterschied zu (1) wird jede Rechteckfunktion $($Dauer $T)$ durch eine Periode einer Sinusfunktionen ersetzt.
- Der angegebene Zahlenwert gibt hier die Amplitude des sinusförmigen Teilstücks an.
- Bei negativem Vorzeichen wird aus dem „Sinus” die Funktion „Minus–Sinus”.
- Mit dem seitlichen Slider kann man die Amplitude von $s_i(t)$ um Vielfache von $\pm 0.25$ vergrößern oder verkleinern.
- Solche Signale können zum Beispiel bei der M–ASK $($mehrstufiges "Amplitude Shift Keying"$)$ auftreten, ebenso bei BPSK $($"Binary Phase Shift Keying"$)$.
(3) Rubrik »$\text{Nur eine Frequenz}$« ⇒ gültig für die Einstellungen $\rm (M)$ ... $\rm (R)$:
- Alle Mustersignale $s_i(t)$ haben die Dauer $T$ und sind jeweils Harmonische Schwingungen der Form
- $$s_i(t) = A_i \cdot \cos(2\pi \cdot f_k \cdot t + \phi_i)\hspace{0.3cm}\text{mit}\hspace{0.3cm}f_k=K/T.$$
- Die Eigenschaft „Nur eine Frequenz” bezieht sich auf die einzelnen Mustersignale $s_i(t)$ und auf den gesamten Set.
- Der Parameter $K$ gibt die Anzahl der Schwingungen innerhalb der Zeit $T$ an und gilt für alle Mustersignale.
- Die Grafik gilt für: $A_i=0.75, \hspace{0.3cm}f_k= 4/T \hspace{0.3cm}\Rightarrow\hspace{0.3cm}K=4, \hspace{0.3cm}\phi_i=- 90^\circ$ ⇒ sinusförmiger Verlauf.
- Mit dem Slider lässt sich die Phase von $s_i(t)$ um Vielfache von $\pm 22.5^\circ$ in beide Richtungen variieren.
- Solche Harmonische haben für alle (analogen und digitalen) Nachrichtensysteme große Bedeutung.
(4) Rubrik »$\text{Mehrere Frequenzen}$« ⇒ gültig für die Einstellungen $\rm (S)$ ... $\rm (X)$:
- Es gelten ähnliche Voraussetzungen wie für die „Rubrik 3”, es sind aber nun stets mehrere Frequenzen beteiligt.
- Die Eigenschaft „Mehrere Frequenzen” bezieht sich auf einzelne Mustersignale $s_i(t)$ oder auch auf den gesamten Set $\{s_i(t)\}$.
- Möglich sind somit auch Mustersignale der folgenden Form $($mit $k=0$ ⇒ $f=f_0 = k/T = 0$ ⇒ Gleichsignal$)$:
- $$s_i(t) = 1 \cdot \cos(2\pi \cdot f_0 \cdot t) - 0.5 \cdot \cos(2\pi \cdot f_2 \cdot t)-0.5 \cdot \cos(2\pi \cdot f_3 \cdot t).$$
- Der Parameter $k$ muss auch nicht ganzzahlig sein. Beispielsweise kennzeichnet $k= 4.5$ viereinhalb Schwingunen Schwingungen innerhalb der Zeitdauer $T$.
- Mit dem Slider können die Frequenzkenngrößen $k$ um Vielfache von $0.25$ vergrößert oder verkleinert werden.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
(1) Es gilt die Einstellung $\rm A$. Interpretieren Sie die ausgegebenen Grafiken. Wählen Sie hierfür „Einzelschritt”.
- Einstellung $\rm A$ beschreibt das $\text{Beispiel 2}$ im Theorieteil. Die Basisfunktion $\varphi_1(t)$ ist identisch mit dem Signal $s_1(t)$, aber mit Signalenergie $E=1$.
- Es gibt hier nur $N=3$ Basisfunktionen, da die Hilfsfunktion $\theta_3(t)$ identisch Null ist.
- Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ können im 3D–Vektorraum abgelesen werden; Beispiel: $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$.
(2) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm B$. Wählen Sie hierfür und bei den weiteren Aufgaben „Gesamtdarstellung”.
- Auch hier gibt es $N=3$ Basisfunktionen. Bei Änderung auf $s_4 = (-1, \hspace{0.15cm} -1, \hspace{0.25cm} 0)$ nur mehr $N=2$.
(3) Bei der Einstellung $\rm C$ ist die Reihenfolge der Signale gegenüber $\rm B$ vertauscht. Wie wirkt sich das auf die Basisfunktionen aus?
- Auch hier gibt es $N=3$ Basisfunktionen, aber nun andere: Nämlich $\varphi_1(t) = s_1(t)$, $\varphi_2(t) = s_2(t)$, $\varphi_3(t) = s_3(t)$.
(4) Die $M=4$ Signale der Einstellung $\rm D$ lassen sich durch nur $N=2$ Basisfunktionen ausdrücken? Begründen Sie dieses Ergebnis.
- Es gilt $s_3(t) = s_1(t)/4 - s_2(t)/2$ und $s_4(t) = -s_1(t) - s_2(t)$. Das heißt: $s_3(t)$ und $s_4(t)$ liefern keine neuen Basisfunktionen.
(5) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm E$ im Vergleich zur Einstellung $\rm D$.
- Bei der Einstellung $\rm E$ ist die Reihenfolge der Signale gegenüber der Einstellung $\rm D$ vertauscht. Ähnlich wie zwischen $\rm B$ und $\rm C$.
- Auch diese $M=4$ Signale lassen sich somit durch nur $N=2$ Basisfunktionen ausdrücken, aber durch andere als in der Aufgabe (4).
(6) Welches Ergebnis liefern die vier Signale gemäß der Einstellung $\rm F$?
- Die die Signale $s_1(t)$, ... , $s_4(t)$ basieren alle auf einer einzigen Basisfunktion $\varphi_1(t)$, die formgleich mit $s_1(t)$ ist. Es gilt $N=1$.
- Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ sind $\pm 0.866$ und $\pm 1.732$. Sie liegen inder 2D–Darstellung alle auf einer Linie.
(7) Es gilt nun die „M–ASK / BPSK”–Einstellung $\rm G$. Interpretieren Sie das Ergebnis und versuchen Sie, einen Zusammenhang zu einer früheren Aufgabe herzustellen.
- Vergleicht man die angegebenen Zahlenwerte, so erkennt man, dass eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm A$.
- Der einzige Unterschied ist, dass nun alle Energien nur halb so groß sind wie vorher. Bezüglich der Amplituden wirkt sich das um den Faktor $\sqrt{2}$ aus.
- Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (-1.021, \hspace{0.15cm} -0.289, \hspace{0.15cm} +0.500)$ anstelle von $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$.
- Bei der Einstellung $\rm H$ sind gegenüber $\rm G$ alle Amplituden verdoppelt. Somit ergibt sich hier $\mathbf{s}_4 = (-2.041, \hspace{0.15cm} -0.577, \hspace{0.15cm} +1.000)$.
(8) Es gelte die „M–ASK / BPSK”–Einstellung $\rm I$. Interpretieren Sie das Ergebnis. Versuchen Sie wieder, einen Zusammenhang zu einer früheren Aufgabe herzustellen.
- Hier wird eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm C$, aber nun mit nur halb so großen Energien.
- Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (+0.707, \hspace{0.15cm} -0.707, \hspace{0.15cm} 0.000)$ anstelle von $\mathbf{s}_4 = (+1.000, \hspace{0.15cm} -1.000, \hspace{0.15cm} 0.000)$.
- Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (+0.707, \hspace{0.15cm} -0.707, \hspace{0.15cm} 0.000)$ anstelle von $\mathbf{s}_4 = (+1.000, \hspace{0.15cm} -1.000, \hspace{0.15cm} 0.000)$.
- Mit der „M–ASK / BPSK”–Einstellung $\rm J$ wird eine ähnliche Konstellation betrachtet wie mit der „Basisband”–Einstellung $\rm D$. Gleiches gilt für $\rm K$ und $\rm E$.
(9) Es gelte die „M–ASK / BPSK”–Einstellung $\rm L$. Interpretieren Sie das Ergebnis. Gibt es einen Zusammenhang zu einer früheren Aufgabe?
- Die Einstellung $\rm L$ ist vergleichbar mit der obigen Einstellung $\rm F$. Es gilt $N=1$. Das heißt:
- Alle $M=4$ Signale sind allein durch die Basisfunktion $\varphi_1(t)$ darstellbar, die formgleich mit $s_1(t)$ ist.
(10) Nun gelte die „Nur eine Frequenz”–Einstellung $\rm M$. Interpretieren Sie die dargestellten Grafiken.
- Alle Signale $s_i(t)$ haben die Amplitude $A_i = 1$ und gleiche Frequenz $f=f_1$. Das heißt: Jeweils eine Schwingung innerhalb der Zeit $T$.
- Die $M=4$ Signale unterscheiden sich nur durch die Phasen $\phi_1 = +45^\circ$, $\phi_2 = +135^\circ$, $\phi_3 = -135^\circ$ und $\phi_4 = -45^\circ$. Es gibt $N=2$ Basisfunktionen.
- Die Basisfunktion $\varphi_1(t)$ ist formgleich mit $s_1(t)$ und $\varphi_2(t)$ ist formgleich mit $s_2(t)$. Dies gilt für die meisten Einstellungen der dritten Rubrik.
- Die vektoriellen Repräsentanten der Signale lauten: $\mathbf{s}_1 = (0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_2 = (0, \hspace{0.15cm} 0.707)$, $\mathbf{s}_3 = (-0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_4 = (0, \hspace{0.15cm} -0.707)$.
(11) Welche Unterschiede gibt es mit der Einstellung $\rm N$ gegenüber der Einstellung $\rm M$?
- Die vier Mustersignale $s_i(t)$ beschreiben nun von oben nach unten einen Cosinus, einen Sinus, einen Minus–Cosinus und einen Minus–Sinus.
- Für die $N=2$ Basisfunktionen gilt: $\varphi_1(t) = \sqrt{2} \cdot \cos(2\pi f_1 t)$, $\varphi_2(t) = \sqrt{2} \cdot\sin(2\pi f_1 t)$. Auch $s_3(t)$ und $s_4(t)$ lassen sich damit beschreiben.
- Die vektoriellen Repräsentanten der Signale lauten: $\mathbf{s}_1 = (0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_2 = (0, \hspace{0.15cm} 0.707)$, $\mathbf{s}_3 = (-0.354, \hspace{0.15cm} 0)$, $\mathbf{s}_4 = (0, \hspace{0.15cm} -0.354)$.
- Dieses Ergebnis berücksichtigt die nur halb so großen Amplituden von $s_3(t)$ und $s_4(t)$ gegenüber $s_1(t)$ und $s_2(t)$.
(12) Wie unterscheidet sich die Einstellung $\rm O$ von der Einstellung $\rm N$? Analysieren Sie den vektoriellen Repräsentanten für $\mathbf{s}_3$ genauer.
- Das Signal $s_2(t)$ bei Einstellung $\rm O$ ist minus–sinusförmig ⇒ $\varphi_1(t) = \sqrt{2} \cdot \cos(2\pi f_1 t)$, $\varphi_2(t) = -\sqrt{2} \cdot\sin(2\pi f_1 t)$.
- Für die Darstellung Harmonischer Schwingungen werden häufig diese Basisfunktionen „Cosinus” und „Minus–Sinus” verwendet.
- Außerdem unterscheiden sich die Signale $s_3(t)$ und $s_4(t)$ durch die halbe Amplitude und die Phsenwerte sind keine Vielfachen von $90^\circ$.
- Die vektoriellen Repräsentanten der Signale lauten: $\mathbf{s}_1 = (0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_2 = (0, \hspace{0.15cm} 0.707)$, $\mathbf{s}_3 = (0.612, \hspace{0.15cm} 0.354)$, $\mathbf{s}_4 = (0.354, \hspace{0.15cm} -0.612)$. Überprüfung:
- $s_3(t) = \cos(2\pi f_1 t + 30^\circ) = \cos(30^\circ) \cdot \cos(2\pi f_1 t)\hspace{-0.05cm} - \hspace{-0.05cm} \sin(30^\circ) \cdot \sin(2\pi f_1 t)=\sqrt{3}/(2\sqrt{2})\cdot \varphi_1(t) + 1/(2\sqrt{2})\cdot \varphi_2(t)= 0.612\cdot \varphi_1(t) + 0.354\cdot \varphi_2(t)$.
(13) Wie unterscheidet sich die Einstellung $\rm P$ von der Einstellung $\rm O$? Gibt es in der Rubrik „Nur eine Frequenz” eine Einstellung für $N=1$ ?
- Mit der Einstellung $\rm P$ ergeben sich gleiche vektorielle Repräsentanten. Einziger Unterschied zur Einstellung $\rm O$ ist die doppelte Frequenz.
- Das Ergebnis $N=1$ ist nur möglich, wenn alle Signale gleiche Frequenz und gleiche Phase besitzen ⇒ Einstellung $\rm R$ $($unterschiedliche Amplituden$)$.
(14) Nun gelte die „Mehrere Frequenzen”–Einstellung $\rm S$. Interpretieren Sie die dargestellten Grafiken.
- Die vier Signale $s_1(t)$ ... $s_4(t)$ weisen nun unterschiedliche Frequenzen auf: $f=0$ (Gleichsignal), $f=f_1$, $f=f_2 = 2f_1$, $f=f_3 = 3f_1$.
- Deshalb ergeben sich hier $N=4$ Basisfunktionen $\varphi_i(t)$, die alle formgleich mit den entsprechenden Signalen $s_i(t)$ sind. Für $i=1$ gilt: $\varphi_1(t)=1$.
- Die weiteren Basisfunktionen haben wegen der Energienormierung einheitlich die Form $\varphi_i(t)= \sqrt{2}\cdot \cos(2\pi f_i t)$.
(15) Wie unterscheidet sich die Einstellung $\rm T$ von der Einstellung $\rm S$? Begründen Sie das Ergebnis $N=3$. Interpretieren Sie auch die Grafiken zur Einstellung $\rm U$.
- Die Signale $s_1(t)$ ... $s_3(t)$ beinhalten die Frequenzen $f=0$, $f=f_1$ und $f=f_2 = 2f_1$. Jedes Signal erzwingt eine eigene Basisfunktion.
- Die vektoriellen Repräsentanten dieser Signale lauten: $\mathbf{s}_1 = (1, \hspace{0.15cm} 0, \hspace{0.15cm} 0)$, $\mathbf{s}_2 = (0, \hspace{0.15cm} 0.707, \hspace{0.15cm} 0)$, $\mathbf{s}_3 = (0, \hspace{0.15cm} 0,\hspace{0.15cm} 0.707)$.
- Das vierte Signal ist als Linearkombination darstellbar: $s_4(t)=s_1(t)-0.5 \cdot s_2(t)-0.5 \cdot s_3(t)$ ⇒ vektorieller Repräsentant: $\mathbf{s}_1 = (1, \hspace{0.15cm} -0.354, \hspace{0.15cm} 0.354)$.
- Die Einstellung $\rm U$ ist nur eine zyklische Vertauschung von der Einstellung $\rm T$ ⇒ es genügen ebenfalls $N = 3$ Basisfunktionen.
- Die $N = 3$ Basisfunktionen sind aber deutlich komplizierter als bei $\rm T$, weil „Gram–Schmidt” signifikant von der Reihenfolge der Mustersignale abhängt.
(16) Interpretieren Sie die dargestellten Grafiken für die Einstellung $\rm V$ und anschließend für die Einstellung $\rm W$.
- Die ersten drei Signale führen zu je einer cosinusförmigen Basisfunktion mit den Frequenzen $f_2$, $f_3$ und $f_4$.
- Das letzte Signal ist $s_4(t)= \cos(2\pi f_3 t) \cdot \cos(2\pi f_1 t) = 1/2 \cdot\big [ \cos(2\pi \cdot (f_3 - f_1)\cdot t) + \cos(2\pi \cdot (f_3 + f_1)\cdot t)\big ] = 1/2 \cdot \big [\cos(2\pi f_2 t) + \cos(2\pi f_4 t)\big ] $.
- Der vektorielle Repräsentant des untersten Signals gemäß Einstellung $\rm V$ lautet somit: $\mathbf{s}_4 = (0.354, \hspace{0.15cm} 0, \hspace{0.15cm} 0.354)$.
- Bei der Einstellung $\rm W$ ergeben sich genau die gleichen Basisfunktionen wie bei $\rm W$. Hier erhält man für das unterste Signal $\mathbf{s}_4 = (0.354, \hspace{0.15cm} 0, \hspace{0.15cm} -0.354)$.
- Begründung $s_4(t)= \sin(2\pi f_3 t) \cdot \sin(2\pi f_1 t) = 1/2 \cdot \big [\cos(2\pi f_2 t) - \cos(2\pi f_4 t)\big ] $. Auch hier liefert die Basisfunktion $\varphi_2(t)$ keinen Beitrag.
(17) Wie viele Basisfunktionen benötigt man für die vier Signale gemäß der Einstellung $\rm X$?
- Das Ergebnis lautet: $N = 4$. Jedes der vier Signale $\cos(2\pi f_1 t)$, $\sin(2\pi f_1 t)$ $\cos(2\pi f_2 t)$, $\sin(2\pi f_2 t)$ führt zu einer neuen Basisfunktion.
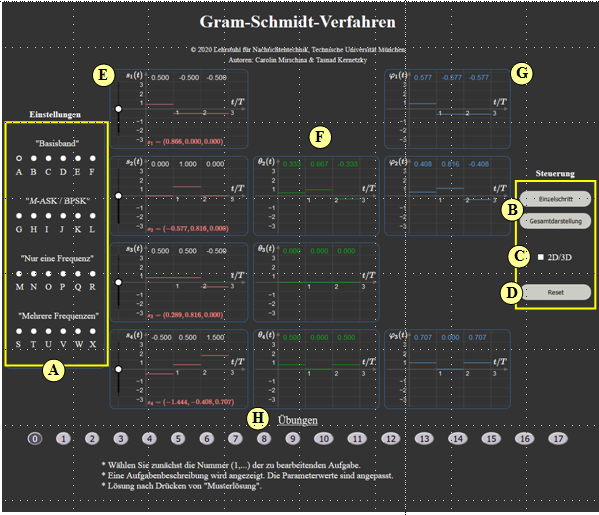
Zur Handhabung des Applets
(A) Auswahl zwischen 24 Parametersätze für $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$
(B) Umschaltung: Einzelschritt / Gesamtdarstellung
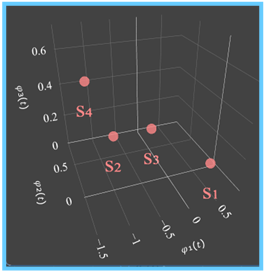
(C) 2D– bzw. 3D–Darstellung der vektoriellen Repräsentanten
(siehe rechte Grafik, Koordinatensystem kann gedreht werden)
(D) Reset – Rücksetzung aller Parameter auf Grundeinstellung
(E) Grafikfeld zur Darstellung der Mustersignale $s_k(t)$
(F) Grafikfeld zur Darstellung der Hilfsfunktionen $\theta_k(t)$
(G) Grafikfeld zur Darstellung der Basisfunktionen $\varphi_k(t)$
(H) Bereich für die Versuchsdurchführung: Aufgabenauswahl
Über die Autoren
Dieses interaktive Berechnungstool wurde am »Lehrstuhl für Nachrichtentechnik« der »Technischen Universität München« konzipiert und realisiert.
- Die erste Version wurde 2008 von »Martin Völkl« im Rahmen seiner Diplomarbeit mit »FlashMX–Actionscript« erstellt $($Betreuer: »Günter Söder«$)$.
- 2020 wurde das Programm von »Carolin Mirschina« im Rahmen einer Werkstudententätigkeit mit „HTML5” neu gestaltet $($Betreuer: »Tasnád Kernetzky«$)$.
Die Umsetzung dieses Applets auf HTML 5 wurde durch das Programm »EXIni« (Exzellenzinitiative) der Technischen Universität München gefördert. Wir bedanken uns.