Signaldarstellung/Analytisches Signal und zugehörige Spektralfunktion: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
David (Diskussion | Beiträge) |
||
| Zeile 19: | Zeile 19: | ||
{{end}} | {{end}} | ||
| + | |||
[[Datei:P_ID710__Sig_T_4_2_S1a.png|250px|right|Analytisches Signal im Frequenzbereich]] | [[Datei:P_ID710__Sig_T_4_2_S1a.png|250px|right|Analytisches Signal im Frequenzbereich]] | ||
| Zeile 26: | Zeile 27: | ||
*bei den negativen Frequenzen zu Null gesetzt. | *bei den negativen Frequenzen zu Null gesetzt. | ||
Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt. | Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt. | ||
| + | |||
| + | |||
| + | |||
{{Beispiel}} | {{Beispiel}} | ||
| + | |||
| + | [[Datei:P_ID711__Sig_T_4_2_S1b_neu.png|300px|right|Beispielspektrum des analytischen Signals]] | ||
| + | |||
Das nachfolgende Bild zeigt links das (komplexe) Spektrum $X(f)$ des BP–Signals | Das nachfolgende Bild zeigt links das (komplexe) Spektrum $X(f)$ des BP–Signals | ||
| Zeile 35: | Zeile 42: | ||
Rechts daneben ist das Spektrum des dazugehörigen analytischen Signals dargestellt. | Rechts daneben ist das Spektrum des dazugehörigen analytischen Signals dargestellt. | ||
| − | |||
| − | |||
{{end}} | {{end}} | ||
| Zeile 54: | Zeile 59: | ||
*Nach den allgemein gültigen Gesetzen der Fouriertransformation entsprechend dem Kapitel 3.3 gilt somit für die Spektralfunktion des Imaginärteils: | *Nach den allgemein gültigen Gesetzen der Fouriertransformation entsprechend dem Kapitel 3.3 gilt somit für die Spektralfunktion des Imaginärteils: | ||
$${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) | $${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) | ||
| − | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{ {\rm | + | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{{\rm |
| − | sign}(f)}{{\rm j}}\cdot X(f).$$ | + | sign}(f)}{ {\rm j}}\cdot X(f).$$ |
*Transformiert man diese Gleichung in den Zeitbereich, so wird aus der Multiplikation die Faltungsoperation, und man erhält: | *Transformiert man diese Gleichung in den Zeitbereich, so wird aus der Multiplikation die Faltungsoperation, und man erhält: | ||
$$y(t) = \frac{1}{{\rm \pi} t} \hspace{0.05cm}\star | $$y(t) = \frac{1}{{\rm \pi} t} \hspace{0.05cm}\star | ||
| Zeile 91: | Zeile 96: | ||
Das Prinzip der Hilbert–Transformation wird durch die untere Grafik nochmals verdeutlicht. Nach der linken Darstellung (A) kommt man vom physikalischen Signal x(t) zum analytischen Signal $x_+(t)$, indem man einen Imaginärteil j · $y(t)$ hinzufügt. Hierbei ist $y(t)$ = H[$x(t)$] eine reelle Zeitfunktion, die sich am einfachsten im Spektralbereich durch die Multiplikation des Spektrums $X(f)$ mit „–j · sign($f$)” angeben lässt. | Das Prinzip der Hilbert–Transformation wird durch die untere Grafik nochmals verdeutlicht. Nach der linken Darstellung (A) kommt man vom physikalischen Signal x(t) zum analytischen Signal $x_+(t)$, indem man einen Imaginärteil j · $y(t)$ hinzufügt. Hierbei ist $y(t)$ = H[$x(t)$] eine reelle Zeitfunktion, die sich am einfachsten im Spektralbereich durch die Multiplikation des Spektrums $X(f)$ mit „–j · sign($f$)” angeben lässt. | ||
| − | [[Datei:P_ID2729__Sig_T_4_2_S2b_neu.png| | + | [[Datei:P_ID2729__Sig_T_4_2_S2b_neu.png|350px|right|Zur Verdeutlichung der Hilbert–Transformierten]] |
Die rechte Darstellung (B) ist äquivalent zu (A). Nun gilt $x_+(t) = x(t) + z(t)$ mit der rein imaginären Funktion $z(t)$. Ein Vergleich der beiden Bilder zeigt, dass tatsächlich $z(t)$ = j · $y(t)$ ist. | Die rechte Darstellung (B) ist äquivalent zu (A). Nun gilt $x_+(t) = x(t) + z(t)$ mit der rein imaginären Funktion $z(t)$. Ein Vergleich der beiden Bilder zeigt, dass tatsächlich $z(t)$ = j · $y(t)$ ist. | ||
| Zeile 130: | Zeile 135: | ||
$$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j} | $$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j} | ||
\varphi_i}\cdot\delta (f - f_{i}) .$$ | \varphi_i}\cdot\delta (f - f_{i}) .$$ | ||
| + | |||
| + | [[Datei:P_ID715__Sig_T_4_2_S4.png|350px|right|Zeigerdiagramm mehrerer Schwingungen]] | ||
Das linke Bild zeigt ein solches Spektrum für das Beispiel $I$ = 3. Wählt man $I$ relativ groß und den Abstand zwischen benachbarten Spektrallinien entsprechend klein, so können mit obiger Gleichung aber auch kontinuierliche Spektralfunktionen angenähert werden. | Das linke Bild zeigt ein solches Spektrum für das Beispiel $I$ = 3. Wählt man $I$ relativ groß und den Abstand zwischen benachbarten Spektrallinien entsprechend klein, so können mit obiger Gleichung aber auch kontinuierliche Spektralfunktionen angenähert werden. | ||
| − | |||
| − | |||
Im rechten Bild ist die dazugehörige Zeitfunktion angedeutet. Diese lautet allgemein: | Im rechten Bild ist die dazugehörige Zeitfunktion angedeutet. Diese lautet allgemein: | ||
| Zeile 163: | Zeile 168: | ||
Zeigerdiagramm – Darstellung des analytischen Signals | Zeigerdiagramm – Darstellung des analytischen Signals | ||
| − | ==Aufgaben | + | ===Aufgaben=== |
| + | [[Aufgaben:4.3 Zeigerdiagrammdarstellung]] | ||
| + | [[Aufgaben:4.4 Zeigerdiagramm beim ZSB-AM]] | ||
Version vom 19. April 2016, 16:02 Uhr
Inhaltsverzeichnis
Definition im Frequenzbereich
Wir betrachten ein reelles bandpassartiges Signal $x(t)$ mit dem dazugehörigen BP–Spektrum $X(f)$, das bezüglich des Frequenznullpunktes einen geraden Real– und einen ungeraden Imaginärteil besitzt. Es wird vorausgesetzt, dass die Trägerfrequenz $f_T$ sehr viel größer als die Bandbreite des BP–Signals $x(t)$ ist.
Das zum physikalischen Signal $x(t)$ gehörige analytische Signal $x_+(t)$ ist diejenige Zeitfunktion, deren Spektrum folgende Eigenschaft erfüllt:
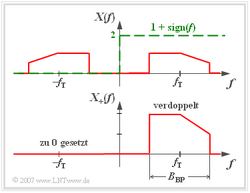
$$X_+(f)=\left[1+{\rm sign}(f)\right] \cdot X(f) = \left\{ {2 \cdot X(f) \; \rm f\ddot{u}r\; {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm f\ddot{u}r\; {\it f} < 0.}}\right.$$
Die so genannte Signumfunktion ist dabei für positive Werte von $f$ gleich +1 und für negative $f$–Werte gleich –1. Der (beidseitige) Grenzwert liefert sign(0) = 0.
Aus der Abbildung erkennt man die Berechnungsvorschrift für $X_+(f)$: Das tatsächliche BP–Spektrum $X(f)$ wird
- bei den positiven Frequenzen verdoppelt, und
- bei den negativen Frequenzen zu Null gesetzt.
Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt.
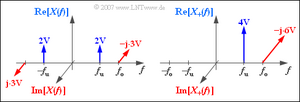
Das nachfolgende Bild zeigt links das (komplexe) Spektrum $X(f)$ des BP–Signals
$$x(t) = 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi f_{\rm u} \hspace{0.03cm}t) + 6\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi f_{\rm o} \hspace{0.03cm}t).$$
Rechts daneben ist das Spektrum des dazugehörigen analytischen Signals dargestellt.
Allgemeingültige Berechnungsvorschrift im Zeitbereich
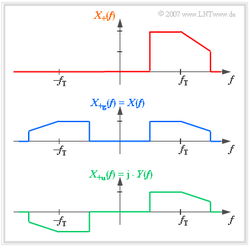
Wir betrachten nun das Spektrum $X_+(f)$ etwas genauer und teilen dieses in einen bezüglich $f$ = 0 geraden und einen ungeraden Anteil auf: $X_+(f) = X_{+g}(f) + X_{+u}(f)$. Alle diese Spektren sind im Allgemeinen komplex.
Berücksichtigt man den Zuordnungssatz der Fouriertransformation, so sind anhand der Grafik folgende Aussagen möglich:
- Der gerade Anteil $X_{+g}(f)$ von $X_{+}(f)$ führt nach der Fouriertransformation zu einem rein reellen Zeitsignal, der ungerade Anteil $X_{+u}(f)$ zu einem rein imaginären.
- Es ist offensichtlich, dass $X_{+g}(f)$ gleich dem tatsächlichen Fourierspektrum $X(f)$ und damit der Realteil von $x_{+g}(t)$ gleich dem vorgegebenen BP–Signal $x(t)$ ist.
- Bezeichnen wir den Imaginärteil mit y(t), so lautet das analytische Signal:
$$x_+(t)= x(t) + {\rm j} \cdot y(t) .$$
- Nach den allgemein gültigen Gesetzen der Fouriertransformation entsprechend dem Kapitel 3.3 gilt somit für die Spektralfunktion des Imaginärteils:
$${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{{\rm sign}(f)}{ {\rm j}}\cdot X(f).$$
- Transformiert man diese Gleichung in den Zeitbereich, so wird aus der Multiplikation die Faltungsoperation, und man erhält:
$$y(t) = \frac{1}{{\rm \pi} t} \hspace{0.05cm}\star \hspace{0.05cm}x(t) = \frac{1}[[:Vorlage:\rm \pi]] \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{{t - \tau}}\hspace{0.15cm} {\rm d}\tau.$$
An dieser Stelle ist es erforderlich, kurz auf eine weitere Spektraltransformation einzugehen, die im Buch Lineare zeitvariante Systeme noch eingehend behandelt wird.
Für die Hilberttransformierte H{ ... } einer Zeitfunktion $x(t)$ gilt:
$$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}[[:Vorlage:\rm \pi]] \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{{t - \tau}}\hspace{0.15cm} {\rm d}\tau.$$
Dieses bestimmte Integral ist nicht auf einfache, herkömmliche Art lösbar, sondern muss mit Hilfe des Cauchy–Hauptwertsatzes ausgewertet werden. Entsprechend gilt im Frequenzbereich:
$$Y(f) = - {\rm j} \cdot {\rm sign}(f) \cdot X(f) \hspace{0.05cm} .$$
Das Ergebnis der letzten Seite lässt sich mit dieser Definition wie folgt zusammenfassen:
- Man erhält aus dem realen, physikalischen BP–Signal $x(t)$ das analytische Signal $x_+(t)$, indem man zu $x(t)$ einen Imaginärteil entsprechend der Hilberttransformierten hinzufügt:
$$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$
- Die Hilberttransformierte $\text{H}\{x(t)\}$ verschwindet nur für das Gleichsignal $x(t)$ = const. Bei allen anderen Signalformen ist das analytische Signal $x_+(t)$ somit stets komplex.
- Aus dem analytischen Signal $x_+(t)$ kann das reale BP–Signal in einfacher Weise durch Realteilbildung ermittelt werden:
$$x(t) = {\rm Re}\left\{x_+(t)\right\} .$$
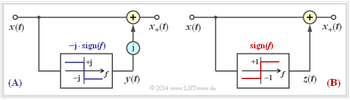
Das Prinzip der Hilbert–Transformation wird durch die untere Grafik nochmals verdeutlicht. Nach der linken Darstellung (A) kommt man vom physikalischen Signal x(t) zum analytischen Signal $x_+(t)$, indem man einen Imaginärteil j · $y(t)$ hinzufügt. Hierbei ist $y(t)$ = H[$x(t)$] eine reelle Zeitfunktion, die sich am einfachsten im Spektralbereich durch die Multiplikation des Spektrums $X(f)$ mit „–j · sign($f$)” angeben lässt.
Die rechte Darstellung (B) ist äquivalent zu (A). Nun gilt $x_+(t) = x(t) + z(t)$ mit der rein imaginären Funktion $z(t)$. Ein Vergleich der beiden Bilder zeigt, dass tatsächlich $z(t)$ = j · $y(t)$ ist.
Zeigerdiagrammdarstellung der harmonischen Schwingung
Die Spektralfunktion $X(f)$ einer harmonischen Schwingung $x(t) = A \cdot \text{cos}(2\pi f_Tt - \phi)$ besteht bekanntlich aus zwei Diracfunktionen bei den Frequenzen
- $+f_T$ mit dem komplexen Gewicht $A/2 \cdot \text{exp}(-\text{j}\cdot \phi)$,
- $-f_T$ mit dem komplexen Gewicht $A/2 \cdot \text{exp}(+\text{j}\cdot \phi)$.
Somit lautet das Spektrum des analytischen Signals:
$$X_+(f) = A \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f - f_{\rm T}) .$$
Die dazugehörige Zeitfunktion erhält man durch Anwendung des Verschiebungssatzes:
$$x_+(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm T} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$
Diese Gleichung beschreibt einen mit konstanter Winkelgeschwindigkeit $\omega_T = 2\pi f_T$ drehenden Zeiger. Aus Darstellungsgründen ist im folgenden Bild das Koordinatensystem entgegen der üblichen Darstellung um 90° nach links gedreht (Realteil nach oben, Imaginärteil nach links).
[[Datei:|P_ID712__Sig_T_4_2_S3.png250px|right|Zeigerdiagramm einer harmonischen Schwingung]]
Anhand dieser Grafik sind folgende Aussagen möglich:
- Zum Startzeitpunkt $t$ = 0 liegt der Zeiger der Länge $A$ (Signalamplitude) mit dem Winkel $-\phi$ in der komplexen Ebene. Im gezeichneten Beispiel gilt $\phi$ = 45°.
- Für Zeiten $t$ > 0 dreht der Zeiger mit konstanter Winkelgeschwindigkeit (Kreisfrequenz) $\omega_T$ in mathematisch positiver Richtung, das heißt entgegen dem Uhrzeigersinn.
- Die Spitze des Zeigers liegt somit stets auf einem Kreis mit Radius $A$ und benötigt für eine Umdrehung genau die Zeit $T_0$, also die Periodendauer.
- Die Projektion des analytischen Signals $x_+(t)$ auf die reelle Achse, durch rote Punkte markiert, liefert die Augenblickswerte des tatsächlichen, reellen BP–Signals $x(t)$.
Zeigerdiagramm einer Summe harmonischer Schwingungen
Für die weitere Beschreibung gehen wir von folgendem Spektrum des analytischen Signals aus:
$$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j} \varphi_i}\cdot\delta (f - f_{i}) .$$
Das linke Bild zeigt ein solches Spektrum für das Beispiel $I$ = 3. Wählt man $I$ relativ groß und den Abstand zwischen benachbarten Spektrallinien entsprechend klein, so können mit obiger Gleichung aber auch kontinuierliche Spektralfunktionen angenähert werden.
Im rechten Bild ist die dazugehörige Zeitfunktion angedeutet. Diese lautet allgemein:
$$x_+(t) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{{\rm j}(\omega_i \cdot\hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$
Zu dieser Grafik ist Folgendes anzumerken:
- Die Skizze zeigt die Ausgangslage der Zeiger zum Startzeitpunkt $t$ = 0 entsprechend den Amplituden $A_i$ und Phasenlagen $\phi_i$.
- Die Spitze des resultierenden Zeigerverbundes ist durch das violette Kreuz markiert. Man erhält durch vektorielle Addition der drei Einzelzeiger für den Zeitpunkt $t$ = 0:
$$x_+(t) = 1 \cdot \cos(60^\circ) - 1 \cdot {\rm j} \cdot \sin(60^\circ)+ 2 +1 \cdot \cos(180^\circ) = 1.500 - {\rm j} \cdot 0.866.$$
- Für Zeiten $t$ > 0 drehen die drei Zeiger mit unterschiedlichen Winkelgeschwindigkeiten $\omega_i = 2\pi f_i$. Der rote Zeiger dreht schneller als der grüne, aber langsamer als der blaue Zeiger.
- Da alle Zeiger entgegen dem Uhrzeigersinn drehen, wird sich auch der resultierende Zeiger $x_+(t)$ tendenziell in diese Richtung bewegen. Zum Zeitpunkt $t$ = 1 μs liegt die Spitze des resultierenen Zeigers für die angegebenen Parameterwerte bei
$$ \begin{align*}x_+(t = 1 {\rm \hspace{0.05cm}\mu s}) & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}60^\circ}\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}40 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} + 2\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}50 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001}- 1\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}60 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} \\ & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}45.6^\circ} + 2\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}18^\circ}- 1\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}21.6^\circ} \approx 1.673- {\rm j} \cdot 0.464.\end{align*}$$
- Die resultierende Zeigerspitze liegt nun aber nicht wie bei einer einzigen harmonischen Schwingung auf einem Kreis, sondern es entsteht eine komplizierte geometrische Figur.
Das folgende Interaktionsmodul zeigt $x_+(t)$ für die Summe dreier harmonischer Schwingungen: Zeigerdiagramm – Darstellung des analytischen Signals
Aufgaben
4.4 Zeigerdiagramm beim ZSB-AM