Lineare zeitinvariante Systeme/Folgerungen aus dem Zuordnungssatz: Unterschied zwischen den Versionen
| Zeile 49: | Zeile 49: | ||
Beispiel: Wir gehen wieder von einem Tiefpass erster Ordnung aus: | Beispiel: Wir gehen wieder von einem Tiefpass erster Ordnung aus: | ||
$$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G}}{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$ | $$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G}}{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$ | ||
| + | Hierbei gibt $f_G$ die 3dB–Grenzfrequenz an, bei der $|H(f)|^2$ auf die Hälfte seines Maximums (bei $f =$ 0) abgesunken ist. Die dazugehörige Impulsantwort $h(t)$ wurde bereits auf der letzten Seite dargestellt, wobei $f_G = 1/(2πT)$ zu setzen ist. | ||
| + | [[Datei:P_ID1754__LZI_T_3_1_S2b_neu.png|400px|Frequenzgang eines Tiefpasses erster Ordnung (Real– und Imaginärteil)]] | ||
| + | |||
| + | Die Grafik zeigt den Realteil (blau) und den Imaginärteil (rot) von $H(f)$. Zusätzlich ist grün–gestrichelt der Betrag dargestellt. Nachdem die beiden Zeitfunktionen $h_g(t)$ und $h_u(t)$ über die Signumfunktion zusammenhängen, sind auch Re{ $H(f)$} und Im{ $H(f)$} fest miteinander verknüpft. Der Zusammenhang ist dabei durch die Hilbert–Transformation gegeben, die nachfolgend beschrieben wird. | ||
| + | {{end}} | ||
Version vom 8. Mai 2016, 19:09 Uhr
Real– und Imaginärteil einer kausalen Übertragungsfunktion (1)
Eine jede kausale Impulsantwort $h(t)$ kann als Summe eines geraden Anteils $h_g(t)$ und eines ungeraden Anteils $h_u(t)$ dargestellt werden, wobei gilt: $$\begin{align*} h_[[:Vorlage:\rm g]](t) & = \frac{1}{2}\cdot \left[ h(t) + h(-t) \right]\hspace{0.05cm},\\ h_[[:Vorlage:\rm u]](t) & = \frac{1}{2}\cdot \left[ h(t) - h(-t) \right] = h_[[:Vorlage:\rm g]](t) \cdot {\rm sign}(t)\hspace{0.05cm} \end{align*}$$.
Hierbei ist die sogenannte Signum–Funktion verwendet: $${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ +1 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} { t < 0,} \\ { t > 0.} \\ \end{array}$$
Beispiel: Die Grafik zeigt diese Aufspaltung für eine kausale exponentiell abfallende Impulsantwort $$h(t) = \left\{ \begin{array}{c} 0 \\ 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c} { t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$
eines Tiefpasses erster Ordnung entsprechend Aufgabe Z1.3.
Man erkennt:
- Für positive Zeiten gilt $h_g(t) = h_u(t) = h(t)/2$.
- Für negative Zeiten unterscheiden sich $h_g(t)$ und $h_u(t)$ nur durch das Vorzeichen.
- Für alle Zeiten gilt $h(t) = h_g(t) + h_u(t)$, auch zum Zeitpunkt $t$ = 0 (durch Kreise markiert).
Real– und Imaginärteil einer kausalen Übertragungsfunktion (2)
Betrachten wir nun den gleichen Sachverhalt im Spektralbereich. Nach dem Zuordnungssatz gilt für die komplexe Übertragungsfunktion: $$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} \hspace{0.05cm},\hspace{5cm}$$
$${\rm Re} \left\{ H(f) \right \} & \quad & \hspace{- 0.6cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_[[:Vorlage:\rm g]](t)\hspace{0.05cm},\\ {\rm j} \cdot {\rm Im} \left\{ H(f) \right\} & \quad & \hspace{- 0.6cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_[[:Vorlage:\rm u]](t)\hspace{0.05cm}.$$ Zunächst soll an einem Beispiel der Zusammenhang zwischen Real– und Imaginärteil des Frequenzgangs $H(f)$ herausgearbeitet werden.
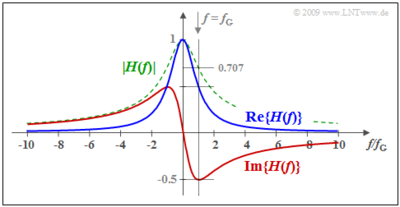
Beispiel: Wir gehen wieder von einem Tiefpass erster Ordnung aus: $$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G}}{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$ Hierbei gibt $f_G$ die 3dB–Grenzfrequenz an, bei der $|H(f)|^2$ auf die Hälfte seines Maximums (bei $f =$ 0) abgesunken ist. Die dazugehörige Impulsantwort $h(t)$ wurde bereits auf der letzten Seite dargestellt, wobei $f_G = 1/(2πT)$ zu setzen ist.
Die Grafik zeigt den Realteil (blau) und den Imaginärteil (rot) von $H(f)$. Zusätzlich ist grün–gestrichelt der Betrag dargestellt. Nachdem die beiden Zeitfunktionen $h_g(t)$ und $h_u(t)$ über die Signumfunktion zusammenhängen, sind auch Re{ $H(f)$} und Im{ $H(f)$} fest miteinander verknüpft. Der Zusammenhang ist dabei durch die Hilbert–Transformation gegeben, die nachfolgend beschrieben wird.