Lineare zeitinvariante Systeme/Folgerungen aus dem Zuordnungssatz: Unterschied zwischen den Versionen
| Zeile 20: | Zeile 20: | ||
{{Beispiel}} | {{Beispiel}} | ||
| − | + | Die Grafik zeigt diese Aufspaltung für eine kausale exponentiell abfallende Impulsantwort | |
$$h(t) = \left\{ \begin{array}{c} 0 \\ | $$h(t) = \left\{ \begin{array}{c} 0 \\ | ||
0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \quad | 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \quad | ||
| Zeile 47: | Zeile 47: | ||
Zunächst soll an einem Beispiel der Zusammenhang zwischen Real– und Imaginärteil des Frequenzgangs $H(f)$ herausgearbeitet werden. | Zunächst soll an einem Beispiel der Zusammenhang zwischen Real– und Imaginärteil des Frequenzgangs $H(f)$ herausgearbeitet werden. | ||
{{Beispiel}} | {{Beispiel}} | ||
| − | + | Wir gehen wieder von einem Tiefpass erster Ordnung aus: | |
$$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G}}{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$ | $$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G}}{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$ | ||
Hierbei gibt $f_G$ die 3dB–Grenzfrequenz an, bei der $|H(f)|^2$ auf die Hälfte seines Maximums (bei $f =$ 0) abgesunken ist. Die dazugehörige Impulsantwort $h(t)$ wurde bereits auf der letzten Seite dargestellt, wobei $f_G = 1/(2πT)$ zu setzen ist. | Hierbei gibt $f_G$ die 3dB–Grenzfrequenz an, bei der $|H(f)|^2$ auf die Hälfte seines Maximums (bei $f =$ 0) abgesunken ist. Die dazugehörige Impulsantwort $h(t)$ wurde bereits auf der letzten Seite dargestellt, wobei $f_G = 1/(2πT)$ zu setzen ist. | ||
| Zeile 55: | Zeile 55: | ||
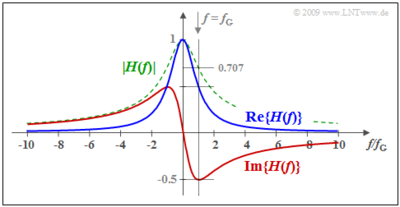
Die Grafik zeigt den Realteil (blau) und den Imaginärteil (rot) von $H(f)$. Zusätzlich ist grün–gestrichelt der Betrag dargestellt. Nachdem die beiden Zeitfunktionen $h_g(t)$ und $h_u(t)$ über die Signumfunktion zusammenhängen, sind auch Re{ $H(f)$} und Im{ $H(f)$} fest miteinander verknüpft. Der Zusammenhang ist dabei durch die Hilbert–Transformation gegeben, die nachfolgend beschrieben wird. | Die Grafik zeigt den Realteil (blau) und den Imaginärteil (rot) von $H(f)$. Zusätzlich ist grün–gestrichelt der Betrag dargestellt. Nachdem die beiden Zeitfunktionen $h_g(t)$ und $h_u(t)$ über die Signumfunktion zusammenhängen, sind auch Re{ $H(f)$} und Im{ $H(f)$} fest miteinander verknüpft. Der Zusammenhang ist dabei durch die Hilbert–Transformation gegeben, die nachfolgend beschrieben wird. | ||
{{end}} | {{end}} | ||
| + | |||
| + | ==Hilbert–Transformation== | ||
| + | Wir betrachten hier ganz allgemein zwei Zeitfunktionen $u(t)$ und $w(t) = sign(t) · u(t)$. Die dazugehörigen Spektralfunktionen sind $U(f)$ und $j · W(f)$. Mit der Fourierkorrespondenz | ||
| + | $${\rm sign}(t) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad \frac{1}{{\rm j} \, \pi f }$$ | ||
| + | erhält man nach Ausschreiben des Faltungsintegrals mit der Integrationsvariablen $ν$: | ||
| + | $${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ | ||
| + | Da aber gleichzeitig auch $u(t) = sign(t) · w(t)$ zutrifft, gilt in gleicher Weise: | ||
| + | $$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | Man benennt diese ''Integraltransformation'' nach ihrem Entdecker David Hilbert. Beide Varianten der Hilbert–Transformation werden im weiteren Verlauf mit folgenden Kurzzeichen gekennzeichnet: | ||
| + | $$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}W(f)= {\cal H}\left\{U(f) \right \}\hspace{0.05cm}.$$ | ||
| + | Zur Berechnung des durch die Pfeilspitze markierten Spektrums – hier $U(f)$ – wird von den beiden ansonsten identischen Gleichungen diejenige mit positivem Vorzeichen genommen. Das durch den Kreis markierte Spektrum – hier $W(f)$ – ergibt sich dagegen aus der Gleichung mit negativem Vorzeichen. | ||
| + | |||
| + | Bei doppelter Anwendung der Hilbert–Transformation erhält man wieder die ursprüngliche Funktion mit Vorzeichenwechsel, bei vierfacher Anwendung die ursprüngliche Funktion inklusive dem Vorzeichen: | ||
| + | $${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f), \hspace{0.2cm} {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} \right \} \right \}= U(f)\hspace{0.05cm}.$$ | ||
| + | {{Beispiel}} | ||
| + | In [Mar94] findet man die folgende Hilbert–Korrespondenz: | ||
| + | $$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$ | ||
| + | Hierbei steht $x$ stellvertretend für eine geeignet normierte Zeit– oder Frequenzvariable. Benutzen wir beispielsweise $x = f/f_G$ als normierte Frequenzvariable, so erhält man daraus die Korrespondenz: | ||
| + | $$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G}}{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$ | ||
| + | Ausgehend von der Gleichung | ||
| + | $${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$ | ||
| + | wird somit das auf der letzten Seite gefundene Ergebnis bestätigt: | ||
| + | $${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G}}{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$ | ||
| + | {{end}} | ||
| + | |||
Version vom 8. Mai 2016, 19:20 Uhr
Real– und Imaginärteil einer kausalen Übertragungsfunktion (1)
Eine jede kausale Impulsantwort $h(t)$ kann als Summe eines geraden Anteils $h_g(t)$ und eines ungeraden Anteils $h_u(t)$ dargestellt werden, wobei gilt: $$\begin{align*} h_[[:Vorlage:\rm g]](t) & = \frac{1}{2}\cdot \left[ h(t) + h(-t) \right]\hspace{0.05cm},\\ h_[[:Vorlage:\rm u]](t) & = \frac{1}{2}\cdot \left[ h(t) - h(-t) \right] = h_[[:Vorlage:\rm g]](t) \cdot {\rm sign}(t)\hspace{0.05cm} \end{align*}$$.
Hierbei ist die sogenannte Signum–Funktion verwendet: $${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ +1 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} { t < 0,} \\ { t > 0.} \\ \end{array}$$
Die Grafik zeigt diese Aufspaltung für eine kausale exponentiell abfallende Impulsantwort $$h(t) = \left\{ \begin{array}{c} 0 \\ 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c} { t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$
eines Tiefpasses erster Ordnung entsprechend Aufgabe Z1.3.
Man erkennt:
- Für positive Zeiten gilt $h_g(t) = h_u(t) = h(t)/2$.
- Für negative Zeiten unterscheiden sich $h_g(t)$ und $h_u(t)$ nur durch das Vorzeichen.
- Für alle Zeiten gilt $h(t) = h_g(t) + h_u(t)$, auch zum Zeitpunkt $t$ = 0 (durch Kreise markiert).
Real– und Imaginärteil einer kausalen Übertragungsfunktion (2)
Betrachten wir nun den gleichen Sachverhalt im Spektralbereich. Nach dem Zuordnungssatz gilt für die komplexe Übertragungsfunktion: $$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} \hspace{0.05cm},\hspace{5cm}$$
$${\rm Re} \left\{ H(f) \right \} & \quad & \hspace{- 0.6cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_[[:Vorlage:\rm g]](t)\hspace{0.05cm},\\ {\rm j} \cdot {\rm Im} \left\{ H(f) \right\} & \quad & \hspace{- 0.6cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_[[:Vorlage:\rm u]](t)\hspace{0.05cm}.$$ Zunächst soll an einem Beispiel der Zusammenhang zwischen Real– und Imaginärteil des Frequenzgangs $H(f)$ herausgearbeitet werden.
Wir gehen wieder von einem Tiefpass erster Ordnung aus: $$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G}}{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$ Hierbei gibt $f_G$ die 3dB–Grenzfrequenz an, bei der $|H(f)|^2$ auf die Hälfte seines Maximums (bei $f =$ 0) abgesunken ist. Die dazugehörige Impulsantwort $h(t)$ wurde bereits auf der letzten Seite dargestellt, wobei $f_G = 1/(2πT)$ zu setzen ist.
Die Grafik zeigt den Realteil (blau) und den Imaginärteil (rot) von $H(f)$. Zusätzlich ist grün–gestrichelt der Betrag dargestellt. Nachdem die beiden Zeitfunktionen $h_g(t)$ und $h_u(t)$ über die Signumfunktion zusammenhängen, sind auch Re{ $H(f)$} und Im{ $H(f)$} fest miteinander verknüpft. Der Zusammenhang ist dabei durch die Hilbert–Transformation gegeben, die nachfolgend beschrieben wird.
Hilbert–Transformation
Wir betrachten hier ganz allgemein zwei Zeitfunktionen $u(t)$ und $w(t) = sign(t) · u(t)$. Die dazugehörigen Spektralfunktionen sind $U(f)$ und $j · W(f)$. Mit der Fourierkorrespondenz $${\rm sign}(t) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad \frac{1}{{\rm j} \, \pi f }$$ erhält man nach Ausschreiben des Faltungsintegrals mit der Integrationsvariablen $ν$: $${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ Da aber gleichzeitig auch $u(t) = sign(t) · w(t)$ zutrifft, gilt in gleicher Weise: $$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$
Man benennt diese Integraltransformation nach ihrem Entdecker David Hilbert. Beide Varianten der Hilbert–Transformation werden im weiteren Verlauf mit folgenden Kurzzeichen gekennzeichnet:
$$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}W(f)= {\cal H}\left\{U(f) \right \}\hspace{0.05cm}.$$
Zur Berechnung des durch die Pfeilspitze markierten Spektrums – hier $U(f)$ – wird von den beiden ansonsten identischen Gleichungen diejenige mit positivem Vorzeichen genommen. Das durch den Kreis markierte Spektrum – hier $W(f)$ – ergibt sich dagegen aus der Gleichung mit negativem Vorzeichen.
Bei doppelter Anwendung der Hilbert–Transformation erhält man wieder die ursprüngliche Funktion mit Vorzeichenwechsel, bei vierfacher Anwendung die ursprüngliche Funktion inklusive dem Vorzeichen: $${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f), \hspace{0.2cm} {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} \right \} \right \}= U(f)\hspace{0.05cm}.$$
In [Mar94] findet man die folgende Hilbert–Korrespondenz: $$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$ Hierbei steht $x$ stellvertretend für eine geeignet normierte Zeit– oder Frequenzvariable. Benutzen wir beispielsweise $x = f/f_G$ als normierte Frequenzvariable, so erhält man daraus die Korrespondenz: $$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G}}{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$ Ausgehend von der Gleichung $${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$ wird somit das auf der letzten Seite gefundene Ergebnis bestätigt: $${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G}}{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$